3. Лінійність перетворення Лапласа.

Теорема 1. Нехай ,-довільні числа. Тоді

.

Доведення.

Теорема 2 (теорема єдності). Якщо , то .

Приклад 1. Знайти зображення функції .

Розв’язання. Функція є оригіналом з показником росту . Оскільки , то за властивістю лінійності маємо при :

.

Вправа. Показати, що: 1) ; 2) ; 3) .

4. Основні теореми.

Теорема 3 (теорема подібності). Якщо , де , то при

,

де .

Доведення. За означенням перетворення Лапласа маємо

,

оскільки .

Приклад 2. Знайти зображення функцій , , , .

Розв’язання. За теоремою подібності

; ;

; .

Теорема 4 (теорема про зміщення зображення). Якщо , , то

,

де .

Доведення. За означенням перетворення Лапласа маємо

,

де .

Приклад 3. Знайти зображення функцій ; .

Розв’язання. За теоремою про зміщення зображення

; .

Теорема 5 (теорема про запізнення). Якщо , то

,

де – довільне додатне число.

Доведення. Функція-оригінал має вигляд: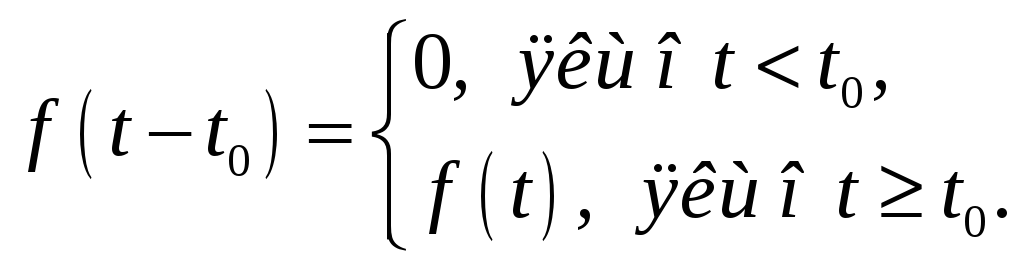

За означенням перетворення Лапласа маємо

.

Перший інтеграл дорівнює нулю, оскільки , коли . У другому інтегралі зробимо заміну . Тоді

Теорема 6 (теорема про випередження). Якщо , то

,

де – довільне додатне число.

Процес, що описується функцією , починається пізніше на час ніж процес, який описується функцією , а відповідно скоріше на , тому і відповідні теореми називаються теоремами запізнювання і випередження.

Теорема 7 (зображення періодичного оригіналу). Якщо – періодична функція, період якої , і, то .

Таблиця основних зображень.

№ п.п.			№ п.п.
1.			7.
2.			8.
3.			9.
4.			10.
5.			11.
6.			12.

Лекція 15.

5. Диференціювання та інтегрування оригіналів та зображень.

Теорема 1 (про диференціювання оригіналу). Нехай і - оригінал, тоді

.

Доведення.

Наслідок. Якщо – оригінали з показником росту і , то

.

Приклад 1. Знайти зображення диференціального виразу за умов

Розв’язання. Позначимо через зображення функції . Тоді відповідно до теореми про диференціювання оригіналу

;

;

.

Тоді,

Теорема 2 (про диференціювання зображення). Якщо , то

Доведення. Оскільки , то

Наслідок.

Приклад 2. Знайти зображення функції .

Розв’язання. Оскільки , то за теоремою про диференціювання зображення

, , , ,,, , .

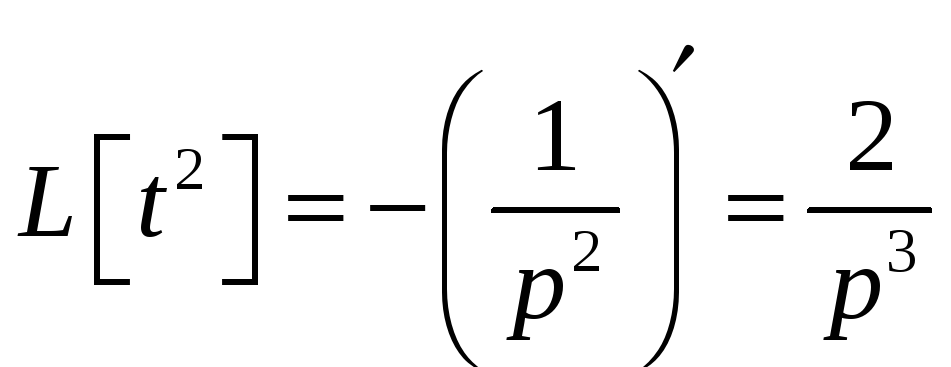Теорема 3 (про інтегрування оригіналу). Якщо і неперервна на інтервалі , то

.

Доведення. Нехай і . Тоді

Приклад 3. Знайти зображення функції .

Розв’язання. Нехай

Тоді

.

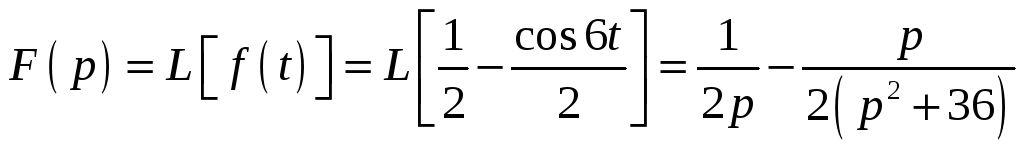За теоремою про інтегрування оригіналу

.

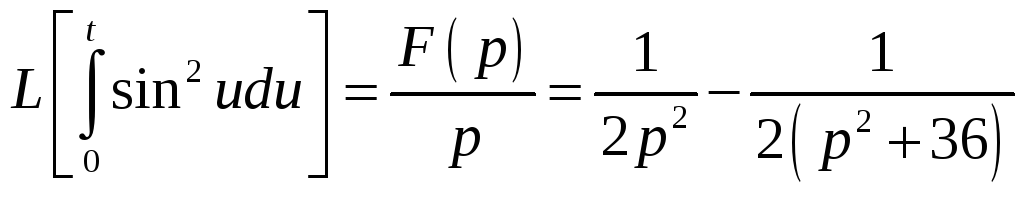Теорема 4 (про інтегрування зображення). Якщо і – оригінал з показником , то

.

Приклад 4. Знайти зображення функції .

Розв’язання. Маємо

Тоді

.

Зауваження. Якщо , то

,

за умови, що обидва невластиві інтеграли збіжні.

Приклад 5.