6. Логарифмічна функція.

Логарифмічна функція комплексної змінної визначається як обернена до показникової:

Комплексне число називається натуральним логарифмом ненульового комплексного числа , якщо виконується рівність .

Нехай ; . Тоді за означенням

; ;

; , .

Звідси – звичайний натуральний логарифм додатного числа ; – вся множина значень аргументу ненульового комплексного числа .

Отже,

.

Останній вираз показує, що функція є нескінченнозначною і визначена на всій комплексній площині, за винятком початку координат .

Нехай в деякій області вибором одного зі значень багатозначної функції одержана деяка однозначна функція . Якщо ця функція неперервна в області , то вона називається однозначною гілкою багатозначної функції .

Зауваження 1. Багатозначну функцію можна розглядати як однозначну, але не на комплексній площині, а на деякому більш складному геометричному об’єкті – Римановій поверхні, що утворюється шляхом “склеювання” певним чином між собою відповідної (скінченної чи нескінченної) кількості ек­земплярів комплексної площини. Наприклад, кореневу функцію можна розглядати як однозначну, множиною визначення якої служить трилиста поверхня (“склеєна” з трьох екземплярів площини), а множиною значень є дволиста поверхня (“склеєна” з двох екземплярів площини).

Однозначну гілку логарифмічної функції можна отримати в будь-якій частині комплексної площини, що не містить початку координат, шляхом виділення відповідного проміжку змінювання його уявної частини.

Якщо для аргументу обмежитися його головним значенням , то одержимо однозначну гілку

,

що називається головним значенням логарифму.

Зауваження 2. Якщо число – дійсне додатне, тоді головне значення аргументу і головне значення логарифму співпадає зі звичайним натуральним логарифмом .

Зауваження 3. На логарифм комплексної змінної поширюються основні властивості звичайного логарифму дійсного аргументу:

; ; .

Область , що відповідає однозначній гілці логарифму, не може включати точку як внутрішню. Точку не можна обійти, залишаючись у цій області, оскільки при кожному обході в заданому напрямі аргумент одержує приріст чи і відбувається перехід до нового значення логарифму . Тому є так званою точкою розгалуження багатозначного логарифму .

Зауваження 4. Точкою розгалуження логарифмічної функції є також .

Зауваження 5. За допомогою логарифмічної функції визначаються:

а) загальна степенева функція , де показник – довільне комплексне число. Ця функція багатозначна, її головне значення .

б) загальна показникова функція , де основа – довільне ненульове комплексне число. Ця функція багатозначна, її головне значення .

в) показниково-степенева функція , де основа відмінна від нуля . Ця функція нескінченнозначна, її головне значення.

7. Обернені тригонометричні і обернені гіперболічні функції.

Багатозначні обернені тригонометричні і обернені гіперболічні функції визначаються як розв’язки відповідних рівнянь для прямих функцій. Переходячи в цих рівняннях за формулами Ейлера до експоненти, вказані аркфункції можна виразити через логарифмічну функцію.

Наприклад, число називається арксинусом комплексного числа , якщо . Позначається . За означенням ; з рівняння знайдемо :

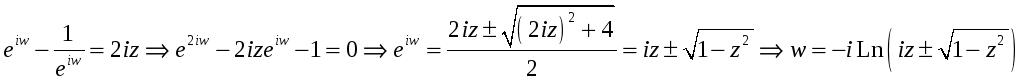Отже, .

Аналогічно виводяться формули для інших обернених тригонометричних і обернених гіперболічних функцій:

; ; .

Приклад 1. Знайти .

Розв’язання. ; .

Приклад 2. Розв’язати рівняння .

Розв’язання.

; . .

Лекція 8.