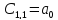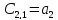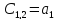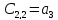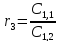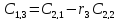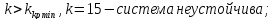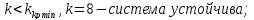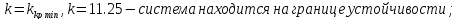лабораторная работа / Отчёт_3

1.1. Заданная структурная схема автоматической системы с заданными значениями параметров.

g y

(-)

T1	0.5
C3	4

1.2. Вывод выражения и само выражение .

Передаточная функция замкнутой автоматической системы имеет вид

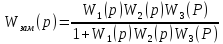
для нашей системы примет следующий вид

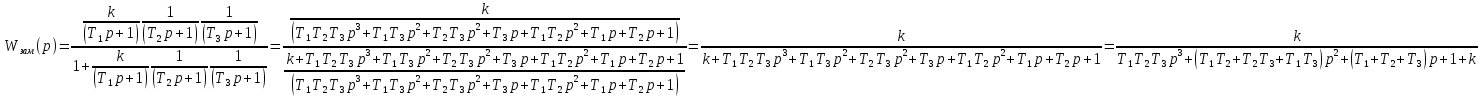
Используя замену

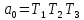
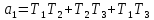
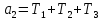
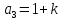
получим

Используя критерий Гурвица найдём 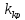, при котором система находится на границе устойчивости. Для этого составим квадратную матрицу коэффициентов

Система устойчива если все определители больше 0

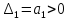
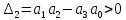
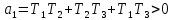
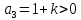
тогда используя , найдём значение

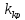
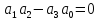
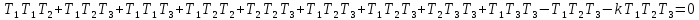
Разделим всё на

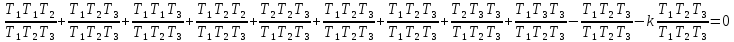
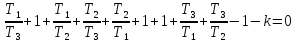
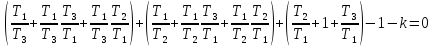
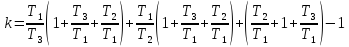
Сделаем замену

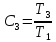
тогда

1.3. Кривая при с устойчивыми и неустойчивыми областями.

1.4. Определение .

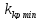Для этого найдём

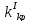
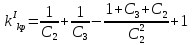
Приравнивая её к нулю найдём

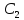
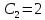
Тогда

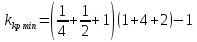
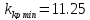
1.5. Три таблицы Рауса.

Критерий Рауса представляет собой алгоритм, по которому составляется специальная таблица, в которой записываются коэффициенты характеристического полинома таким образом, что:

1. в первой строке записываются коэффициенты уравнения с чётными индексами в порядке их возрастания

2. во второй строке — с нечётными

3. остальные элементы таблицы определяется по формуле: ,

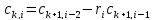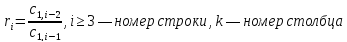
4. число строк таблицы Рауса на единицу больше порядка характеристического уравнения

ri	i\n	1	2
-	1
-	2
	3		-

Для устойчивости линейной стационарной системы необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса были одного знака. Если это не выполняется, то система неустойчива.

1.5.1

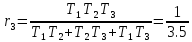
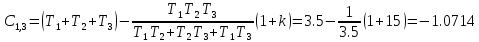
Видим что коэффициент 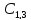отрицателен в отличии от двух других, значит что система неустойчива при

1.5.2

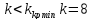
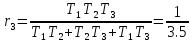
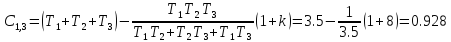
Видим что все коэффициенты первого столбца одного знака, значит что система устойчива при

1.5.2

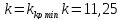
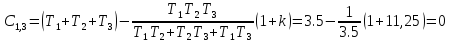
Коэффициент 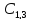равен нулю, значит система находится на границе устойчивости.

1.6. Три кривые Михайлова.

Для устойчивости системы необходимо и достаточно, чтобы кривая Михайлова проходила поочередно n квадрантов против часовой стрелки, окружая всё время начало координат.

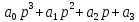
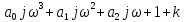
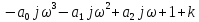
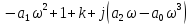
1)

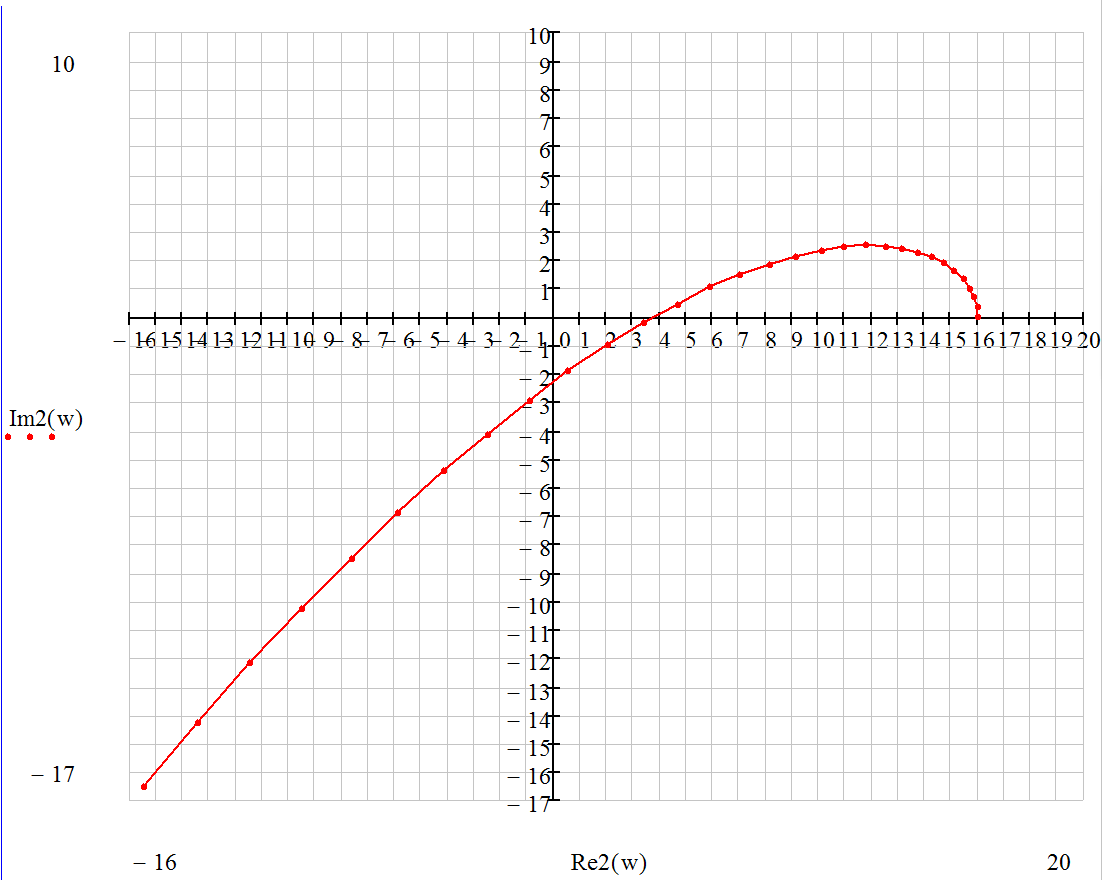
Система неустойчива, т.к. кривая проходит квадранты не последовательно, а именно 1-4-3.

2)

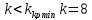
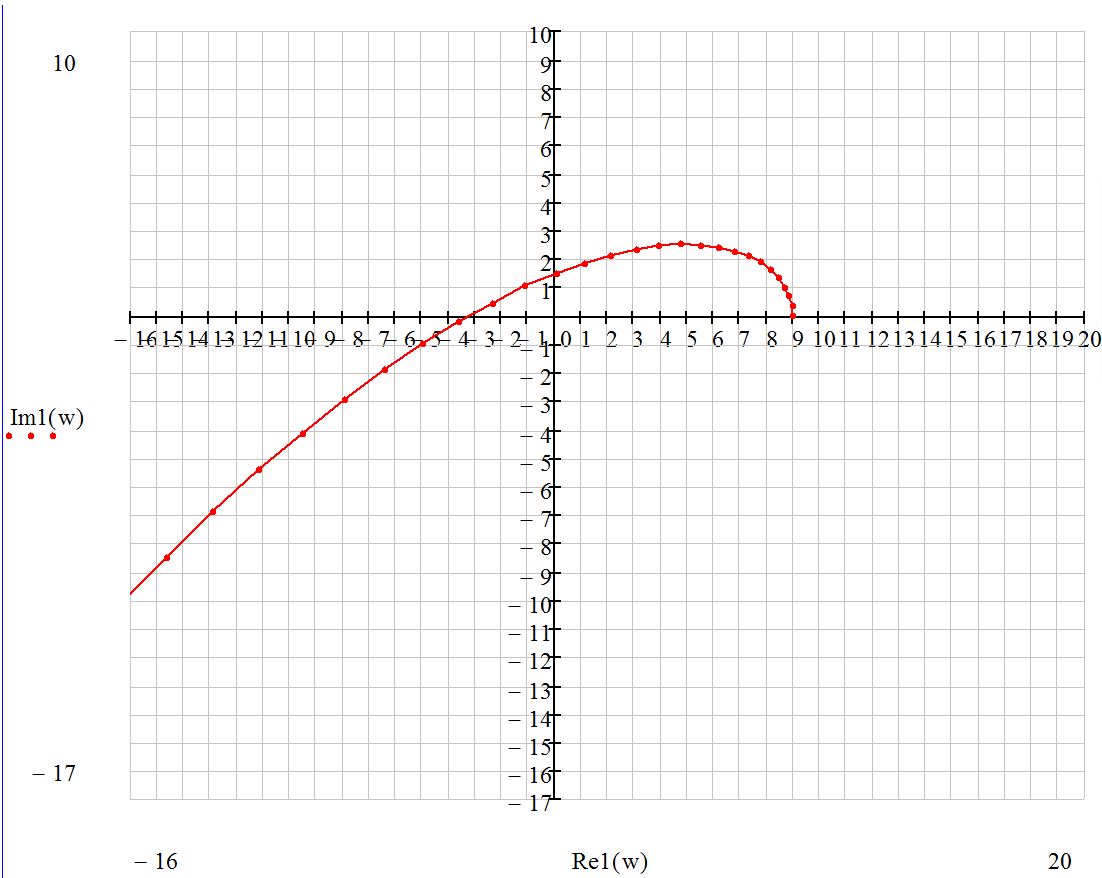
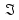
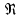
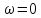
Система устойчива, т.к. критерии Михайлова выполняются.

3)

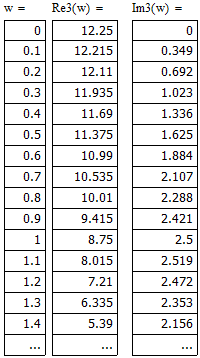
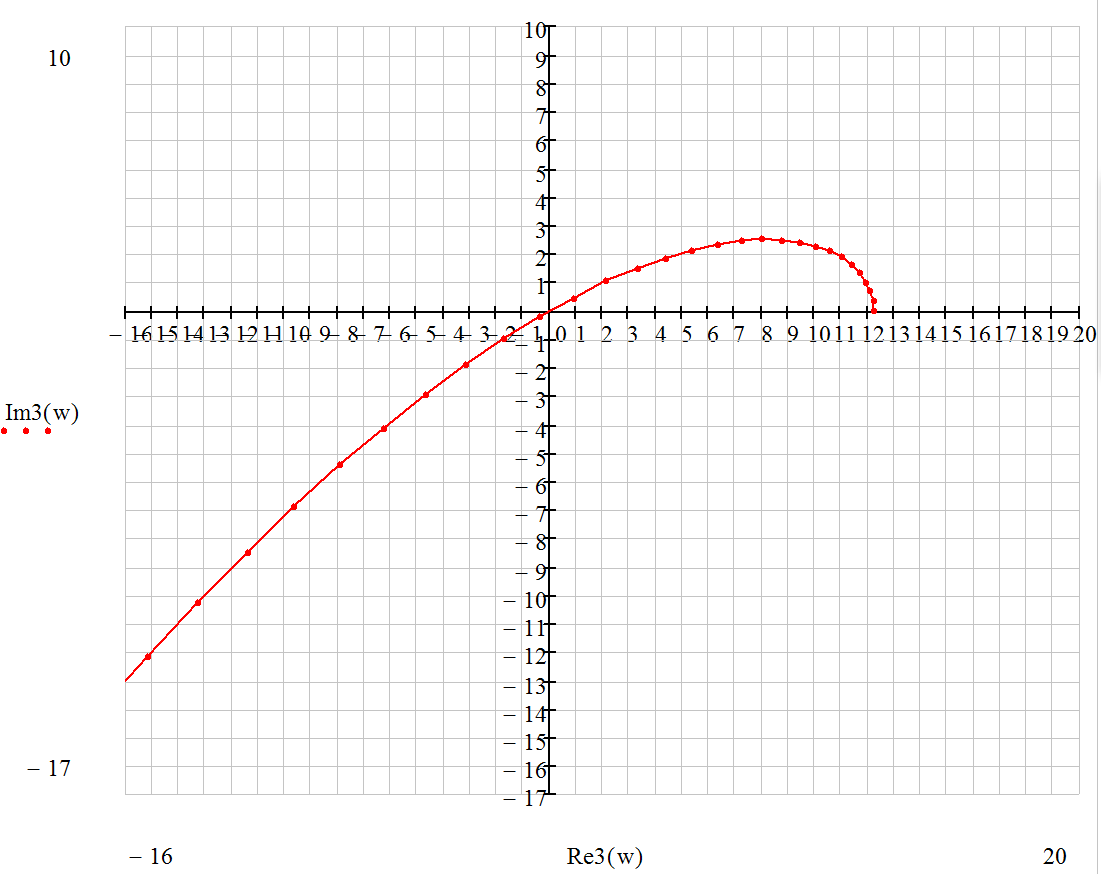
Система находится на грани устойчивости.

1.7. Три амплитудно-фазовые характеристики разомкнутой автоматической системы.

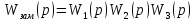
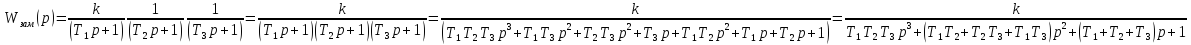
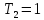
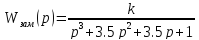
1)

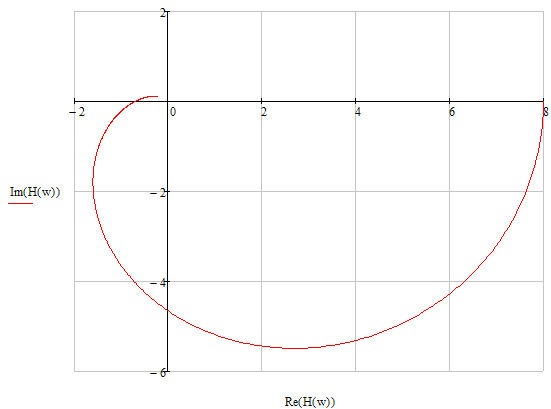
2)

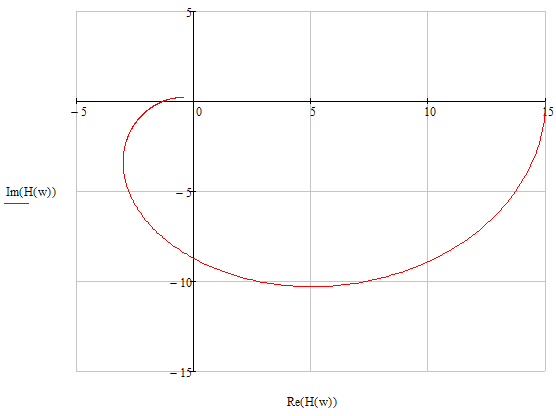
3)

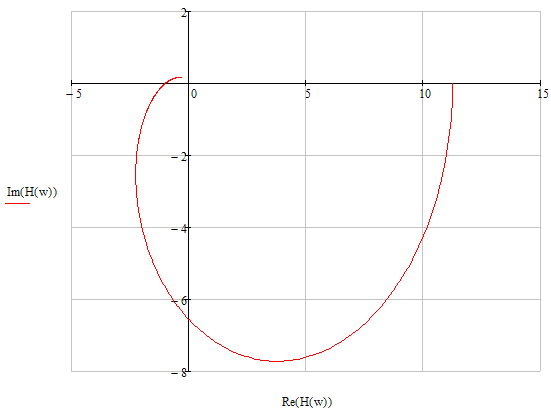
1.8. Листинг фрагмента программы, относящийся к моделированию заданной автоматической системы.

begin

y1:=0; y2:=0; y3:=0;

T:=0;

g:=1;

repeat

k1:= dt*(k[i]*g-y1)/T1;

k2:= dt*(k[i]*g-(y1+k1/2))/T1;

k3:= dt*(k[i]*g-(y1+k2/2))/T1;

k4:= dt*(k[i]*g-(y1+k3))/T1;

y1:=y1+(k1+2*k2+2*k3+k4)/6;

g:=y1;

k1:= dt*(g-y2)/T2;

k2:= dt*(g-(y2+k1/2))/T2;

k3:= dt*(g-(y2+k2/2))/T2;

k4:= dt*(g-(y2+k3))/T2;

y2:=y2+(k1+2*k2+2*k3+k4)/6;

g:=y2;

k1:= dt*(g-y3)/T3;

k2:= dt*(g-(y3+k1/2))/T3;

k3:= dt*(g-(y3+k2/2))/T3;

k4:= dt*(g-(y3+k3))/T3;

y3:=y3+(k1+2*k2+2*k3+k4)/6;

g:=1-y3;

Chart4.Series[i-1].AddXY(T,y3);

T:=T+dt;

until T>=L;

end;

end;

1.9. Результаты моделирования.

1. 

2. 

3. 

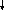
Список использованной литературы:

1. Куцый, А.С. Основы теории управления. Лабораторный практикум: лабораторные работы № 1-5 / Н.Н. Куцый. – Иркутск: ИрГУПС, 2008. – 72 с.

2. Теория систем автоматического регулирования / В. А. Бесекерский, Е. П. Попов. - Изд. 2-е , испр. и доп. - М. : Наука, 1972. - 767 с. : a-a-ил