лабораторная работа / Положения равновесия и устойчивость нелинейных систем

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

ФАКУЛЬТЕТ ИНЖЕНЕРНО - СТРОИТЕЛЬНЫЙ

Практическая работа

по ТАУ

«Положения равновесия и устойчивость нелинейных систем»

Вариант №9

Выполнил:

ст. гр. УИТ-44

Макаров Д.А.

Принял:

Скоробогатова Т.Н.

2007

Цель работы: Исследовать устойчивость систем с нелинейными характеристиками, найти и оценить устойчивость имеющихся положений равновесия.

Задание:

Дифференциальные уравнения объектов -

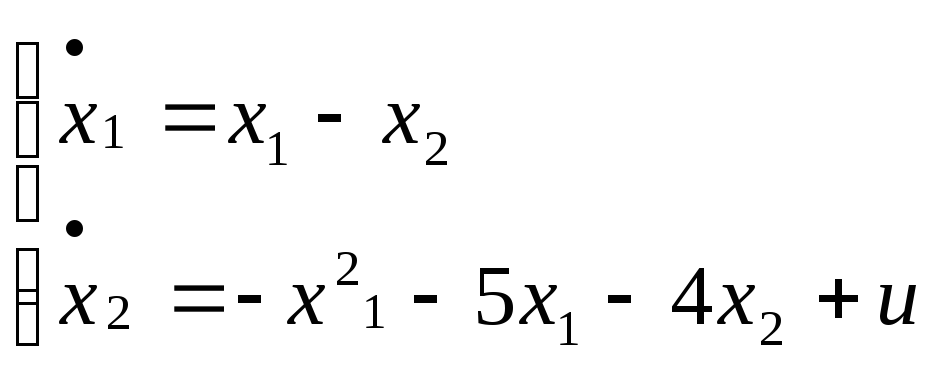
u = 4;

Коэффициенты системы: а₀=0,41; а₁=1.

Структурная схема системы:

1) Определим положения равновесия. Для этого приравняем производные к нулю.

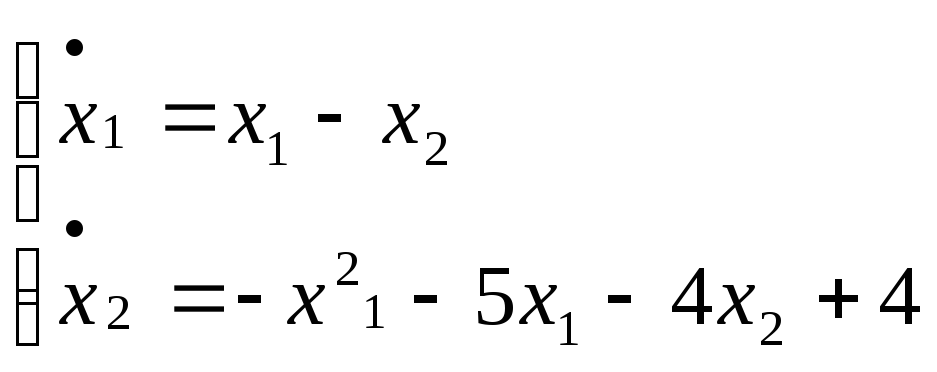
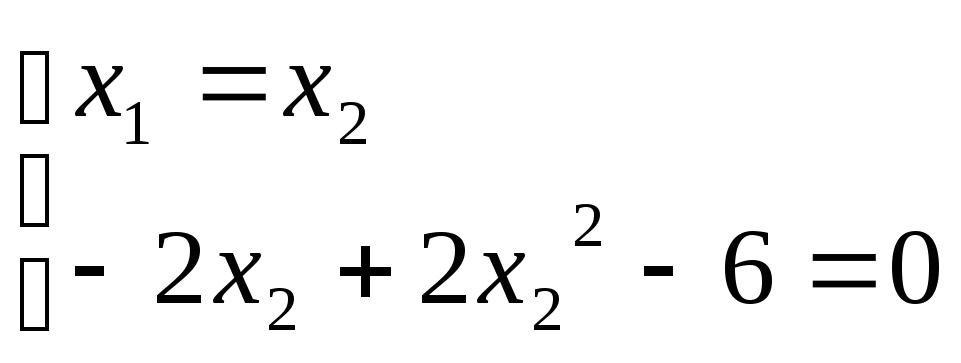
Корни получились действительные, значит, положение равновесия существует.

С учетом коэффициентов, заданных по варианту, получим следующую структурную схему:

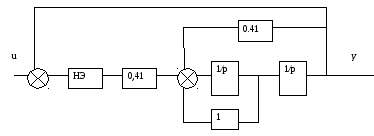
Определим общую передаточную функцию линейной части системы. Используя правила преобразования структурных схем, получим:

Тогда структурная схема примет вид:

2) Построим фазовый портрет системы.

Передаточную функцию можно записать в виде или , подставляя в эту формулу значение передаточной функции, получим:

Приведенную формулу можно записать в виде:

Воспользуемся пакетом MathCad для решения этого дифференциального уравнения. Введем замену pⁱx=y_i и исключим из левой части уравнения производные выше второго порядка. В итоге получим уравнение :

1) Рассмотрим нелинейность вида:

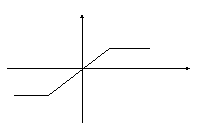
Создадим матрицу для решения дифференциального уравнения:

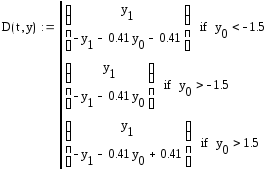
В данной матрице реализовано условие перехода от одного уравнения к другому. Зададим матрицу начальных условий:

Возьмем количество точек равным 1000 и конечное время интегрирования 100, то матрица решений запишется как:

.

По введенным данным получим фазовый портрет:

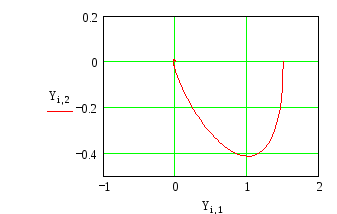
На рисунке представлен фазовый портрет нелинейной системы. Характер фазовой линии такой, что она постоянно приближается к началу координат, то есть нелинейная система с релейным элементом устойчива.

Построим переходный процесс системы.

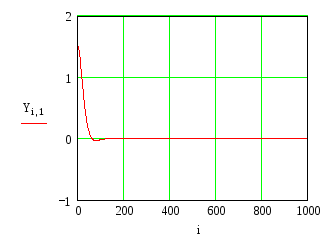
График переходного процесса стремится к установившемуся значению, что еще раз показывает устойчивость данной системы с нелинейностью релейного типа.

Определим перерегулирование и время переходного процесса:

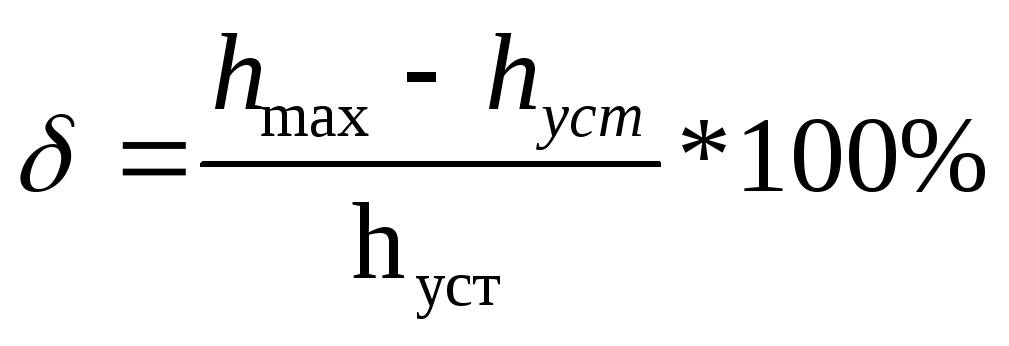1. перерегулирование . Так как h_уст=0 , то определить перерегулирование для данной системы не допустимо.

2. Время переходного процесса t_п = 127.

2) Рассмотрим нелинейность вида:

Создадим матрицу для решения дифференциального уравнения:

В данной матрице реализовано условие перехода от одного уравнения к другому. Зададим матрицу начальных условий:

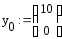
Возьмем количество точек равным 1000 и конечное время интегрирования 100, то матрица решений запишется как:

.

По введенным данным получим фазовый портрет:

На рисунке представлен фазовый портрет нелинейной системы. Характер фазовой линии такой, что она постоянно приближается к началу координат, то есть нелинейная система с релейным элементом устойчива.

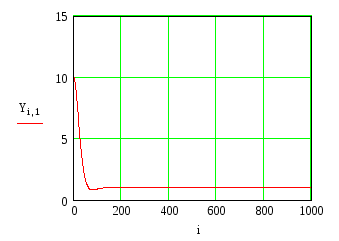
График переходного процесса стремится к установившемуся значению, что еще раз показывает устойчивость данной системы с нелинейностью релейного типа.

Определим время переходного процесса:

1. Время переходного процесса t_п = 115.

Вывод: В ходе практической работы была исследована устойчивость системы с различными видами нелинейностей. Исходная система оказалась устойчива во всех случаях, так как фазовый портрет стремился к началу координат, а график переходного процесса оказался сходящимся.