Цель работы: Знакомство с нелинейными САУ и методами их исследования с помощью фазовых траекторий и припасовывания.

На рисунке 1 изображена исследуемая нелинейная система.

Рисунок 1

Нелинейный элемент представляет собой чувствительный элемент со статической характеристикой в виде релейной характеристики с зоной нечувствительности (рисунок 2г).

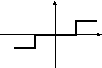
Рисунок 2.

Передаточная функция исполнительного устройства:

(1)

Передаточная функция объекта регулирования:

(2)

Линейная часть системы описывается уравнением:

(3)

Уравнение нелинейного элемента имеет вид:

(4)

Уравнение сравнивающего элемента:

(5)

Предположим, что задающее воздействие x(t)=0. Тогда уравнение нелинейной САУ будет иметь вид:

(6)

Характеристика нелинейного элемента разбивается на три линейных участка и для каждого из них составляется линейное дифференциальное уравнение:

1уч. , если

2уч. , если (7)

3уч. , если

Для фазовой плоскости введем координаты y . Исключим в уравнениях время t.

(8)

Разделяя переменные и интегрируя, получим уравнения фазовых траекторий для участков 1-3 нелинейной характеристики.

1уч.

2уч. (9)

3уч.

где - постоянные интегрирования, определяемые начальными условиями.

На основании системы уравнений (9) и исходных данных, запишем уравнения фазовых траекторий исследуемой нелинейной системы:

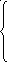, если

, если

, если

В MathCad программа получения фазовых траекторий на фазовой плоскости для заданной нелинейной САУ путем непосредственного решения уравнений (9) имеет следующий вид:

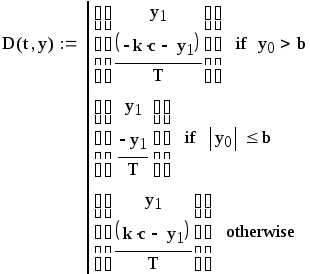
На графике 1 представлен фазовый портрет исследуемой нелинейной системы.

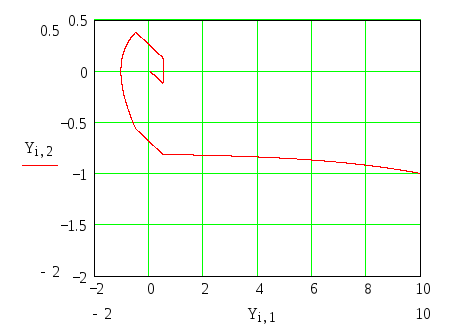
График 1. Фазовый портрет

На графике 2 представлен переходный процесс исследуемой нелинейной системы.

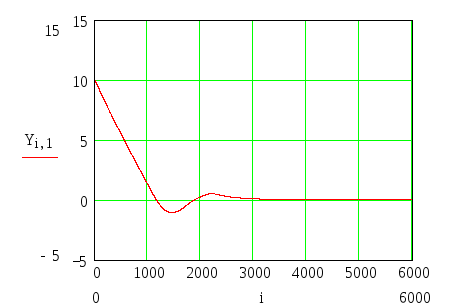
График 2. Переходный процесс

Вывод: В процессе работы была исследована нелинейная САУ методом припасовывания, а также изучен метод фазовых переменных. Исследованная нелинейная система является устойчивой.