лабораторная работа / лаб1тау

Министерство образования и науки Украины

Одесский национальный политехнический университет

Лабораторная работа №1

«Временные характеристики типовых динамических звеньев»

Выполнил:

студент группы АЕ-083

Файт А.О.

Проверил:

Андриевский Г.Г.

Одесса 2010

Цель работы – изучение временных характеристик типовых динамических звеньев; ознакомление с методикой экспериментального получения на модели этих характеристик, а также с методами определения параметров динамических звеньев по их переходным характеристикам.

Рекомендуется данную работу выполнить в два этапа. На первом этапе провести исследование звеньев: апериодического первого порядка, интегрирующего, реального дифференцирующего. На втором этапе – звено второго порядка апериодическое и колебательное.

Ход выполнения работы.

1. Апериодическое звено 1-го порядка.

Звено этого типа описывается дифференциальным уравнением первого порядка

(1)

Передаточная функция имеет вид

Если на вход такого звена подать ступенчатое воздействие, то на выходе возникнет переходный процесс (переходная характеристика), имеющий вид экспоненты, что и определило название звена.

Коэффициент усиления звена может быть определен из выражения

Переходная функция

(2)

Постоянную времени звена можно определить по переходной характеристике как время, за которое выходная величина изменится от нуля до , где - установившееся значение на выходе звена.

Действительно при уравнение имеет вид

Приведем три графика переходных процессов для различных значений коэффициента усиления и постоянной времени .

1.1 К=1, Т=0.8 с.

Передаточная функция

Найдем значение y(t) которое соответствует значению t=T:

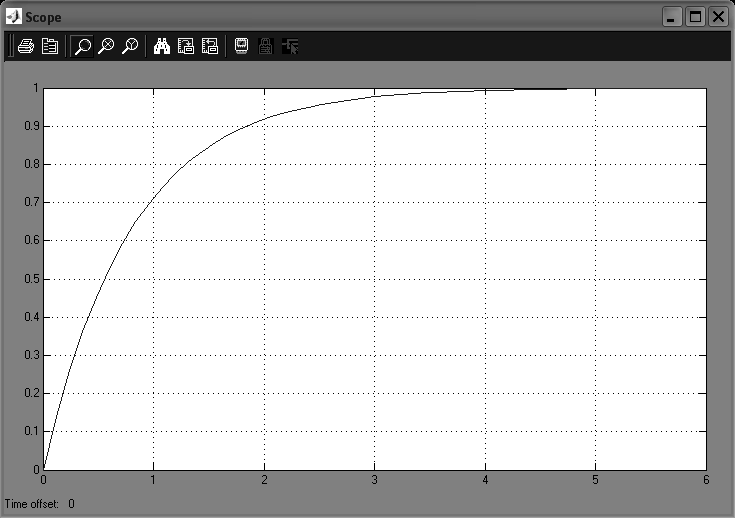
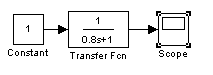
Рис 1.1 переходная характеристика апериодического звена 1-го порядка

(К=1, Т=0.8)

1.2 К =1, Т=0.1 с.

Передаточная функция

Найдем значение y(t) которое соответствует значению t=T:

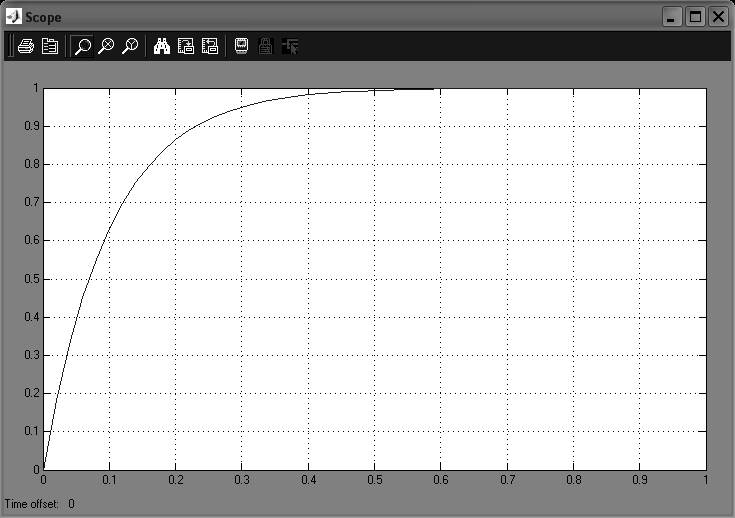
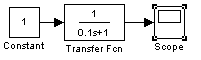
Рис 1.2 переходная характеристика апериодического звена 1-го порядка

(К=1, Т=0.1)

1.2 К =2, Т=0.1 с.

Передаточная функция

Найдем значение y(t) которое соответствует значению t=T:

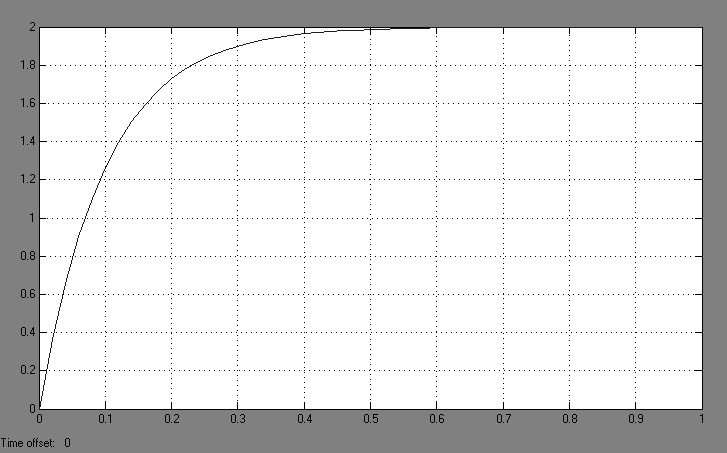
Рис 1.3 Переходная характеристика апериодического звена 1-го порядка

(К=2, Т=0.1)

2. Интегрирующее звено

Выходная величина этого звена пропорциональна интегралу от входной величины:

или

Передаточная функция такого звена имеет вид:

, где

В данной работе К=5.

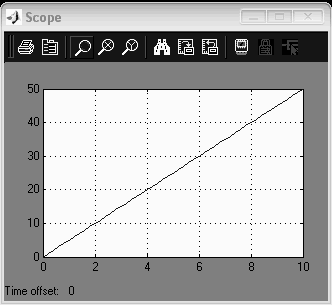
Рис 2.1 Переходная характеристика интегрирующего звена

(К=5)

3. Дифференцирующее звено.

Передаточная функция идеального дифференцирующего звена имеет вид

В идеале реакция дифференцирующего звена на входной ступенчатый сигнал

имеет вид импульса, бесконечно большого по величине и бесконечно малого по длительности.

В реальности любое звено имеет инерционные свойства. Поэтому дифференцирующее звено будем исследовать как последовательно включенные идеальное дифференцирующее звено с передаточной функцией и апериодическое звено первого порядка с передаточной функцией . Общая переходная функция получится:

В данной работе значение , .

По графику переходной характеристики звена можно определить значения постоянных , Т. Начальное значение характеристики равно . Постоянная времени Т численно равна времени, в течение которого выходная величина изменится от до 0.368 . В данном случае:

при t=T y=0.368*5=1.84

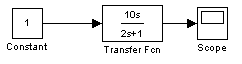
Рис 3.1 Переходная характеристика дифференцирующего звена

(τ=10, Т=2)

4. Звено 2-го порядка.

Звено этого типа описывается дифференциальным уравнением в операторной форме

или

(3)

где - коэффициент затухания.

Передаточная функция имеет вид:

Из последнего выражения видно, что подобное звено может быть представлено как последовательно включенные два апериодических звена первого порядка.

И в зависимости от значения коэффициента затухания ξ переходная характеристика колебательного звена может иметь разный характер. Если ξ>0 то характеристика апериодическая, схожая на характеристику звена 1-го порядка. ξ >1 то характеристика колебательная, затухающая. Если ξ =0 то переходная характеристика имеет незатухающий колебательный характер.

Исследуем эти три случая.

4.1 К=5, Т=0.8, ξ=1,8

Передаточная функция

Переходная характеристика апериодическая.

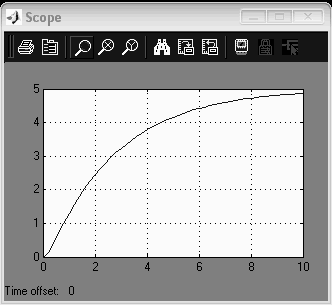
Рис 4.1 переходная характеристика апериодического звена 2-го порядка

(К=5, Т=0.8 с. ξ=1.8)

4.2 К=5, Т=0.8, ξ=0

Передаточная функция

Переходная характеристика имеет вид бесконечных незатухающих колебаний.

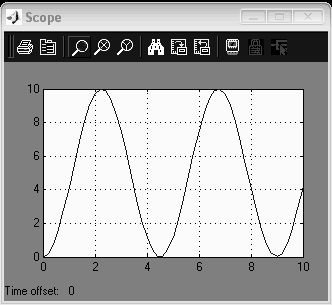
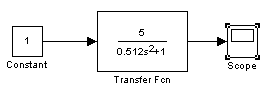
Рис 4.1 переходная характеристика апериодического звена 2-го порядка

(К=5, Т=0.8 с. ξ=0)

4.2 К=5, Т=0.8, ξ=0.15

Передаточная функция

Переходная характеристика имеет вид затухающих колебаний.

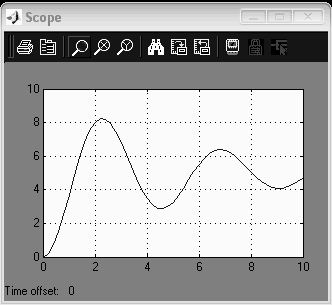
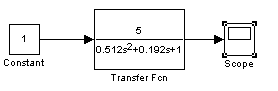
Рис 4.1 переходная характеристика апериодического звена 2-го порядка

(К=5, Т=0.8 с. ξ=0.15)

Выводы. В данной работе мы изучили временные характеристики типовых динамических звеньев; ознакомились с методикой экспериментального получения на модели этих характеристик, а также с методами определения параметров динамических звеньев по их переходным характеристикам.