
лабораторная работа / лаба 3 (2)
.docМинистерство образования РФ
Балаковский институт техники, технологии и управления
Лабораторная работа по ТАУ № 3
ИССЛЕДОВАНИЕ МНОГОМЕРНЫХ СИСТЕМ В ПРОСТРАНСТВЕ СОСТОЯНИЙ
Выполнил ст. гр. УИТ-41
Печавин А. В.
Проверил: Мартынова И. В.
Балаково, 2004
Цель работы: ознакомление с описанием и исследованием динамических многомерных систем управления в пространстве состояний.
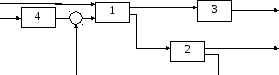
Даны три линейные стационарные системы, структурная схема соединения которых представлена на рисунке.
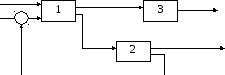
+
1.
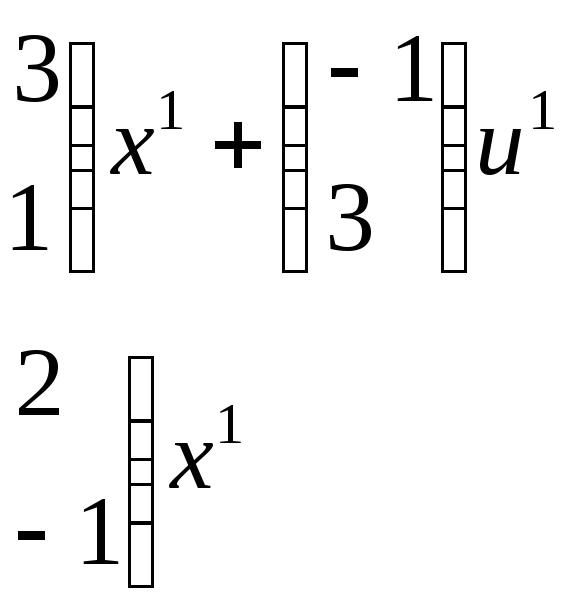
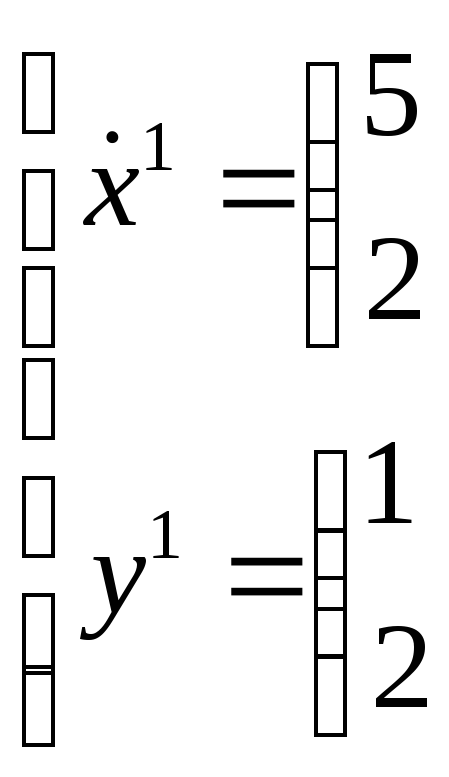
![]()

2.
3.

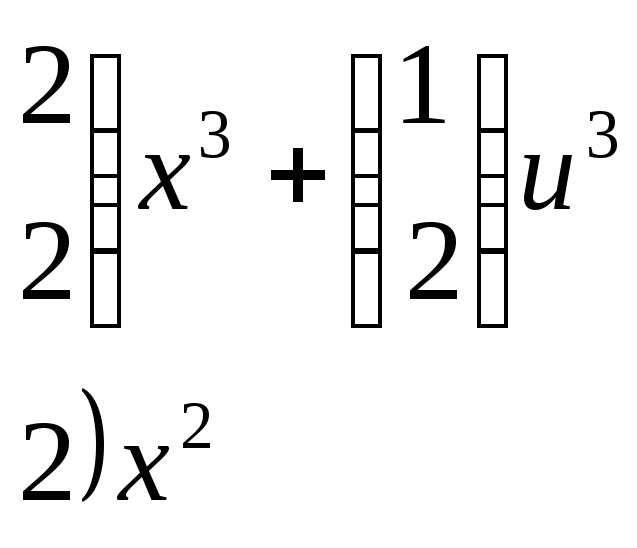
-
Системы представлены в виде:
 (t)
= A(t)x(t)
+ B(t)u(t);
(t)
= A(t)x(t)
+ B(t)u(t);
y(t) = C(t)x(t);
здесь x = (x1, x2, … xn)T є Rn – вектор переменных воздействий;
u = (u1, u2, … ur)T є U ≤ Rn – вектор управлений;
y = (y1, y2, … ym)T є Rn – вектор измеряемых параметров;
t – время;
A(t),
B(t), C(t)
– матрицы размерности (n![]() n),
(n
n),
(n![]() r),
(m
r),
(m![]() n).
n).
-
Создадим матрицы первой системы.
A1=[5 3;2 1]
A1 =
5 3
2 1
>> B1=[-1;3]
B1 =
-1
3
>> C1=[1 2;2 -1]
C1 =
1 2
2 -1
Создадим, аналогично, матрицы двух других систем:
>> A2=[1 0;1 2]
A2 =
1 0
1 2
>> B2=[1 1;2 1]
B2 =
1 1
2 1
>> C2=[5 -2;2 3]
C2 =
5 -2
2 3
>> A3=[1 2;3 2]
A3 =
1 2
3 2
>> B3=[1;2]
B3 =
1
2
>> C3=[-1 2]
C3 =
-1 2
Создадим ss-объекты:
>> s1=ss(A1, B1, C1,0)
a =
x1 x2
x1 5 3
x2 2 1
b =
u1
x1 -1
x2 3
c =
x1 x2
y1 1 2
y2 2 -1
d =
u1
y1 0
y2 0
Continuous-time model.
>> s2=ss(A2, B2, C2,0)
a =
x1 x2
x1 1 0
x2 1 2
b =
u1 u2
x1 1 1
x2 2 1
c =
x1 x2
y1 5 -2
y2 2 3
d =
u1 u2
y1 0 0
y2 0 0
Continuous-time model.
>> s3=ss(A3, B3, C3,0)
a =
x1 x2
x1 1 2
x2 3 2
b =
u1
x1 1
x2 2
c =
x1 x2
y1 -1 2
d =
u1
y1 0
Continuous-time model.
-
Исследуем наблюдаемость и управляемость каждой системы, для чего построим соответствующие матрицы и посчитаем их ранги.
>> rank(ctrb(A1,B1))
ans =
2
>> rank(obsv(A1,C1))
ans =
2
>> rank(ctrb(A2,B2))
ans =
2
>> rank(obsv(A2,C2))
ans =
2
>> rank(ctrb(A3,B3))
ans =
2
>> rank(obsv(A3,C3))
ans =
2
Видно, что во всех случаях ранги матриц управляемости и наблюдаемости совпадают с размерностями пространства состояний.
4. Получим систему, определяемую соединением.
Для корректного использования функции connect введем дополнительную систему, передаточная функция которой равна.
1 1 4 5
5 6 2
+ 2
3 3
4
>> s4=tf(1)
Transfer function:
1
>> sys=append(s1,s2,s3,s4)
a =
x1 x2 x3 x4 x5 x6
x1 5 3 0 0 0 0
x2 2 1 0 0 0 0
x3 0 0 1 0 0 0
x4 0 0 1 2 0 0
x5 0 0 0 0 1 2
x6 0 0 0 0 3 2
b =
u1 u2 u3 u4 u5
x1 -1 0 0 0 0
x2 3 0 0 0 0
x3 0 1 1 0 0
x4 0 2 1 0 0
x5 0 0 0 1 0
x6 0 0 0 2 0
c =
x1 x2 x3 x4 x5 x6
y1 1 2 0 0 0 0
y2 2 -1 0 0 0 0
y3 0 0 5 -2 0 0
y4 0 0 2 3 0 0
y5 0 0 0 0 -1 2
y6 0 0 0 0 0 0
d =
u1 u2 u3 u4 u5
y1 0 0 0 0 0
y2 0 0 0 0 0
y3 0 0 0 0 0
y4 0 0 0 0 0
y5 0 0 0 0 0
y6 0 0 0 0 1
Continuous-time model.
>> Q=[2 4 6;3 2 0;4 1 0]
Q =
2 4 6
3 2 0
4 1 0
>> in=[1 5]
in =
1 5
>> out=[5 3]
out =
5 3
>> s_com=connect(sys,Q,in,out)
a =
x1 x2 x3 x4 x5 x6
x1 5 3 0 0 0 0
x2 2 1 0 0 0 0
x3 2 -1 3 3 0 0
x4 2 -1 5 8 0 0
x5 1 2 0 0 1 2
x6 2 4 0 0 3 2
b =
u1 u2
x1 -1 0
x2 3 0
x3 0 1
x4 0 2
x5 0 0
x6 0 0
c =
x1 x2 x3 x4 x5 x6
y1 0 0 0 0 -1 2
y2 0 0 5 -2 0 0
d =
u1 u2
y1 0 0
y2 0 0
Continuous-time model.
Обращаясь к данным объекта, можно получить матрицы А, В, С:
>> A=s_com.A
A =
5 3 0 0 0 0
2 1 0 0 0 0
2 -1 3 3 0 0
2 -1 5 8 0 0
1 2 0 0 1 2
2 4 0 0 3 2
>> B=s_com.B
B =
-1 0
3 0
0 1
0 2
0 0
0 0
>> C=s_com.C
C =
0 0 0 0 -1 2
0 0 5 -2 0 0
5. Вычислим ранги матриц наблюдаемости и управляемости итоговой системы:
>> rank(ctrb(A,B))
ans =
6
>> rank(obsv(A,C))
ans =
6
Результаты показывают, что система управляема и наблюдаема.
