лабораторная работа / laboratornaya_rabota_5_issledovanie_avtokolebatelnyh_rezhimo

Министерство общего и профессионального образования Российской Федерации

Уфимский государственный авиационный технический университет

Кафедра ТК

Лабораторная работа № 5

по дисциплине «Теория автоматического управления».

Исследование автоколебательных режимов в нелинейных системах

Вариант 5.

Выполнил: студент гр. РС – 320

Кравчук Д.И.

Проверила:

Сильнова С.В.

Уфа

2010

Исходные данные:

№ варианта Параметры	5
K1	2,5
K2	5
K3	1
K4	2
K5	1
T1	0,3
T2	0,5
B	1
C	1

1. Исследование нелинейной САУ 2-го порядка

Модель:

Снимаем осциллограммы переходных процессов на выходе системы x(t) для различных уровней ступенчатого задающего воздействия g(t):

g(t) = 1(t); g(t) = 2(t); g(t) = 3(t).

а) g(t) = 1(t);

t_рег=1,61

б) g(t) = 2(t)

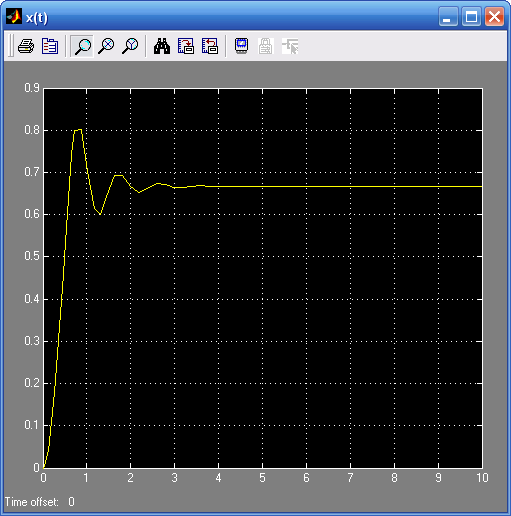
t_рег=1,42

в) g(t) = 3(t)

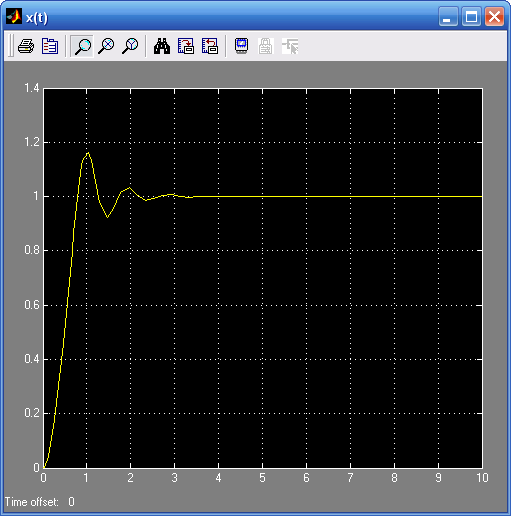
t_рег=1,58

2. Исследование нелинейной САУ 3-го порядка

Модель:

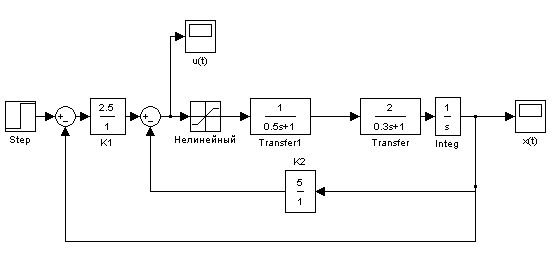
Получит автоколебания на входе нелинейного элемента u(t),

полагая: g(t) = 0; g(t) = 1(t). Измерить амплитуду и частоту этих автоколебаний. Оценить влияние K₄ на характер процессов.

а) g(t) = 0

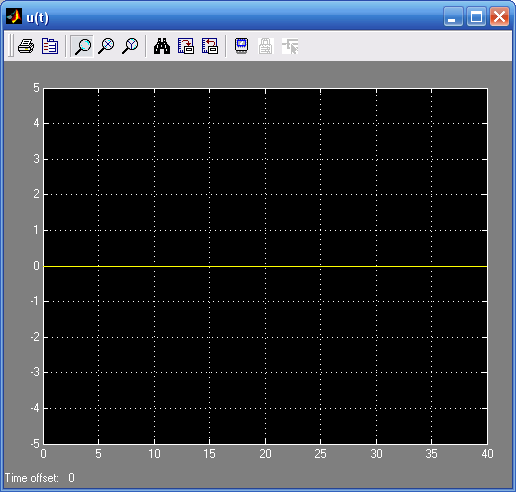
Автоколебания не возникают.

б)

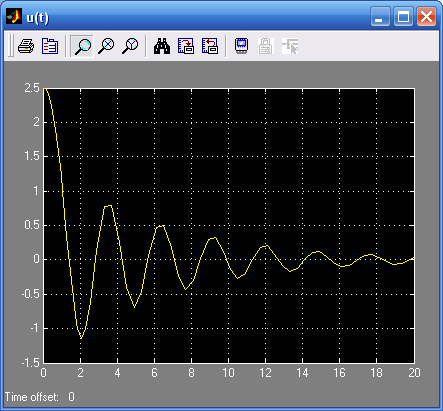
g(t) = 1(t) K₄=2

А=3,55

Т=2,47 с

ω=2π/Т=2,54 Гц

При g(t) = 1(t) K₄=0,5

Автоколебаний нет

При g(t) = 1(t) K₄=4

А=7,225

Т=2,48

ω=2π/Т=2,53 Гц

Вывод: при увеличении К₄ растет амплитуда АК и уменьшается их частота до предельного значения ω_min= 2,51327412287183.

3)САУ 2-го порядка с нелинейностью типа "гистерезис"

Модель:

Снимаем зависимость (3 - 4 точки) амплитуды А и частоты ω этих автоколебаний в функции от параметра В - ширины петли гистерезиса.

К₁=2,5 К₂=5

а)При В=0,5

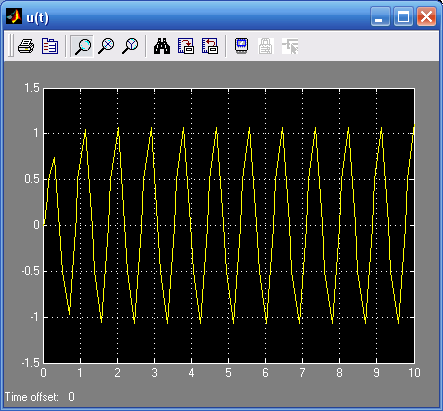
А=1,07

Т=0,89

ω=2π/Т=7,06 Гц

б)При В=1

А=1,83

Т=1,17

ω=2π/Т=5,37 Гц

в)При В=1,5

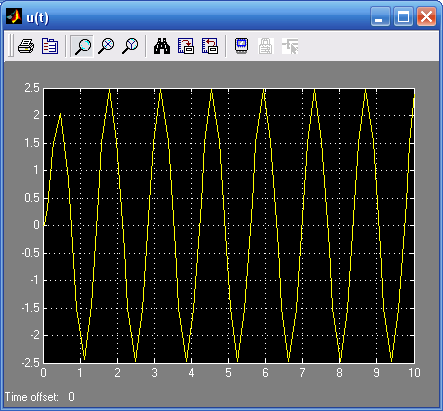
А=2,48

Т=1,385

ω=2π/Т=4,54 Гц

г) При В=2

А=3,1

Т=1,57

ω=2π/Т=4,002 Гц

4)Расчетная часть:

Найти передаточную функцию замкнутой система (s), рассматривая поведение системы в "малом" (нелинейный элемент работает на линейном участке характеристики).

K₁

K₃

K₄

T₁ s + 1

K₅

s

g(t) y(t) x(t)

- -

K₂

Подставим значения коэффициентов и постоянных времени согласно варианту:

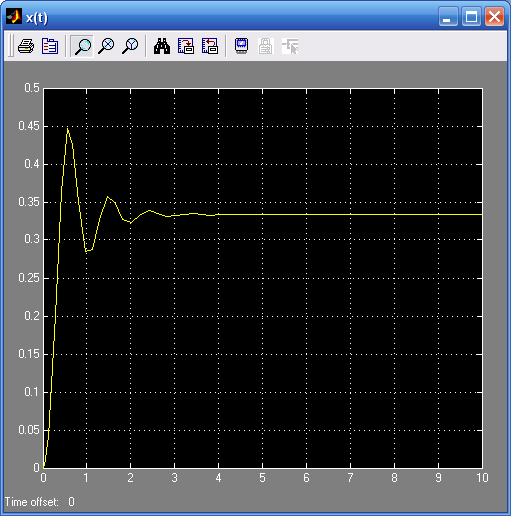
t_рег=1,61

Приведем струтурную схему нелинейной сау 3-го порядка:

K₃

K₁

K₄

T₁ s + 1

1

T₂ s +1

K₅

s

g(t) u(t) y(t) x(t)

- -

K₂

К виду:

НЭ

F(x)

x(t) y(t)

ЛЧ

W_л(s)

x(t) y(t)

и получим:

u(t) y(t)

K₄

T₁ s + 1

1

T₂ s +1

K₅

s

x(t)

K₂

-

K₁

-

g(t)

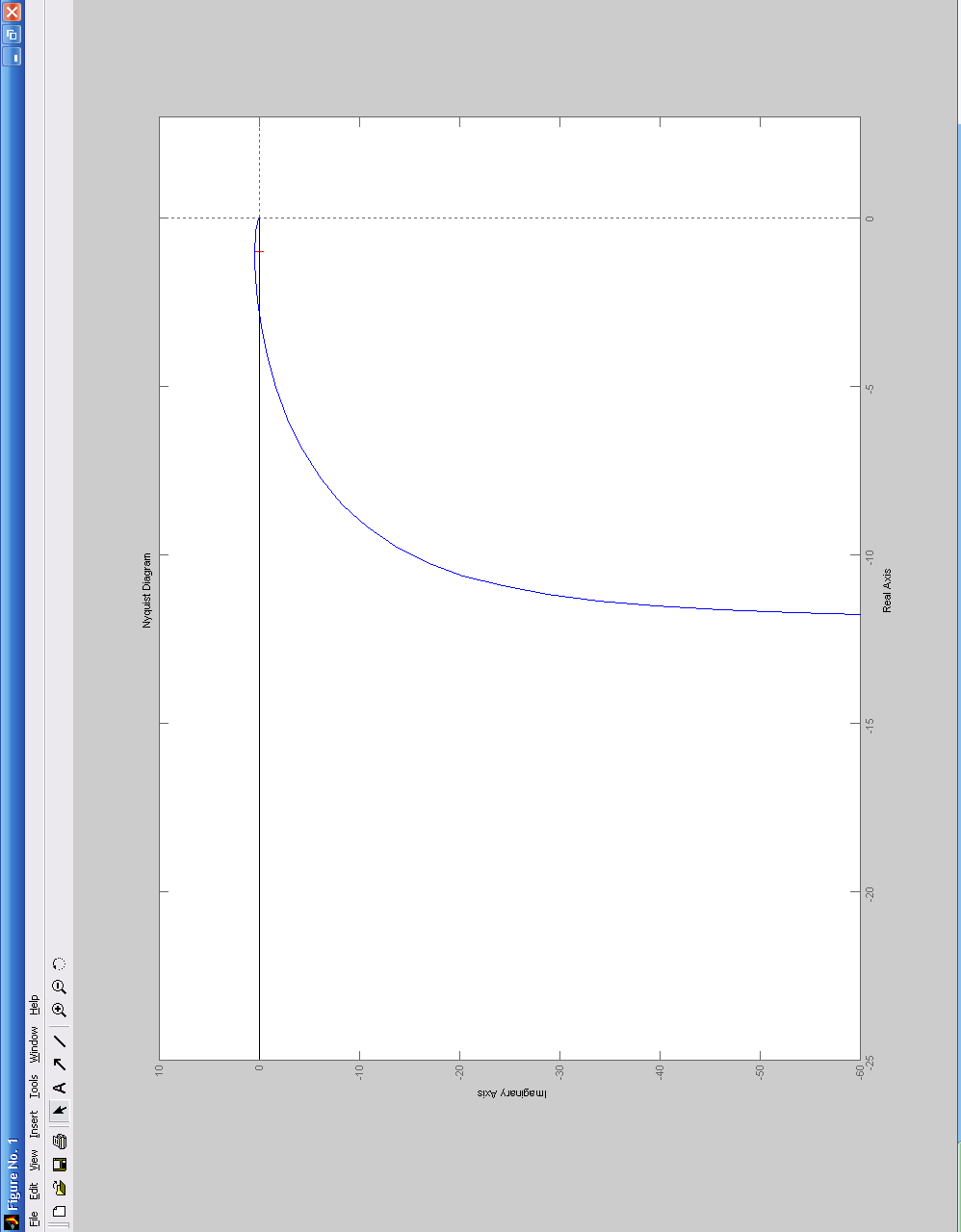
а) АФХ линейной части (jω):

При S → jω:

АФХ:

Определяем зависимость инверсного коэффициента передачи нелинейного элемента от амплитуды автоколебаний: -1/W_н(A):

Для данного вида нелинейности:

при

K=1 B=1

При А→0 → 0

При А→∞ → - ∞

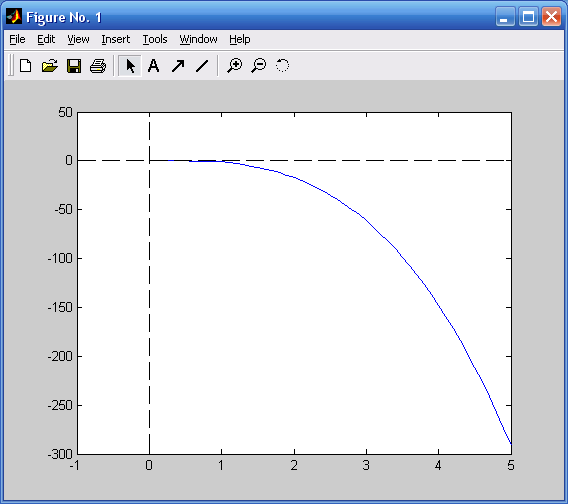
Найдем ω и А исходя из тождества:

Приравниваем мнимые и действительные части:

Откуда найдем:

ω=2.5819888974716112568;

А=4.3489674636824454866.

3) Для нелинейности типа “гистерезис”:

C

-B +B

g

K₁

K₄

T₁ s + 1

K₅

s

(t) u(t) y(t) x(t)

- -

K₂

При S → jω:

А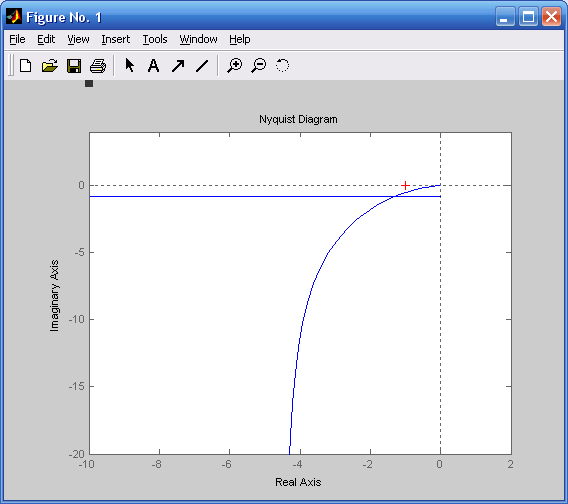ФХ:

Нелинейная составляющая:

В=1 С=1

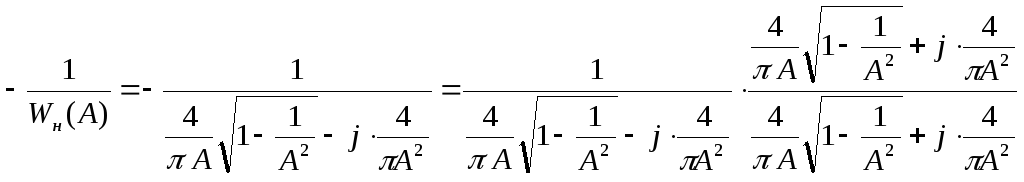
При А→0 → 0

При А→∞ → - ∞

Найдем ω и А исходя из тождества:

Приравниваем мнимые и действительные части:

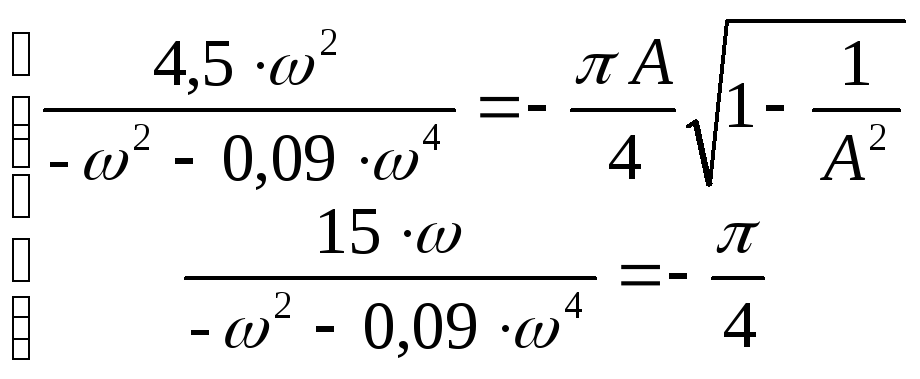
Откуда найдем:

ω= 5.346223375166773441;

А= 5.4389337190298614633.

4)Нелинейность типа реле с зоной нечувствительности:

Нелинейная составляющая:

В=1 С=1

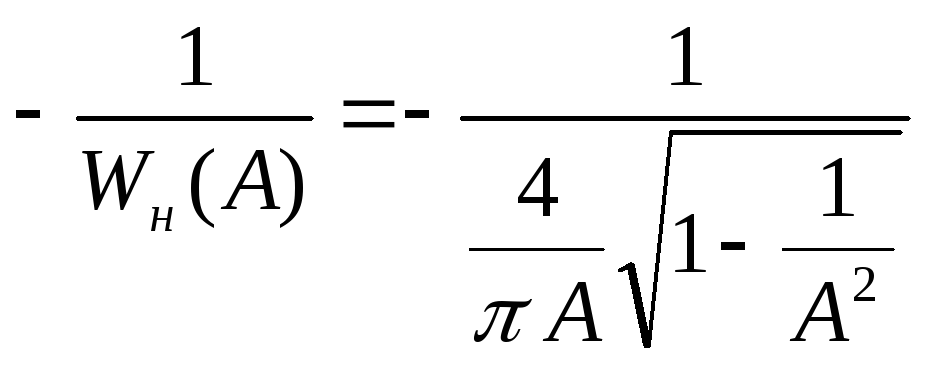
Приравниваем мнимые и действительные части:

При А→0 → - ∞

При А→∞ → - ∞

Вывод:

В ходе лабораторной работы было определено:

а) в схеме с нелинейностью типа насыщение возникают устойчивые автоколебания с «мягким» возбуждением

б) в схеме с нелинейностью типа «гистерезис» возникают устойчивые автоколебания с «мягким» возбуждением

в) в схеме с нелинейностью типа реле возникают устойчивые автоколебания с «жестким возбуждением» возбуждением

19