Выходные координаты автомата

На рис. 24-29 представлены графики выхода автомата (Y(t) и Y(t)) для рассмотренных выше случаев вращения вала.

Рис. 24. График Y(t) при вращении вала по часовой стрелке

Рис. 25. График Y(t) при вращении вала по часовой стрелке

Рис. 26. График Y(t) при вращении вала против часовой стрелки

Рис. 27. График Y(t) при вращении вала против часовой стрелки

Рис. 28. График Y(t) при сбое во вращении вала

Рис. 29. График Y(t) при сбое во вращении вала

Задание на лабораторную работу

Создать модель автомата описанного объекта с исполь­зо­ва­нием компьютера.

Исследовать поведение модели при различных исходных данных — X(t) и X(t):

1. вращение вала по часовой стрелке;

2. вращение вала против часовой стрелки;

3. вращение вала со сбоем;

4. произвольное вращение вала.

В отчете необходимо представить для каждого варианта исходных данных графики:

1. координат входа автомата — X(t) и X(t);

2. состояний автомата — Z(t);

3. координат выхода автомата — Y(t) и Y(t).

Приложение 1

а) временная диаграмма

б) фазовая диаграмма

Рис. 30. Лабораторная работа №1. Параметры решения: D > 0, , (A₀=1, A₁= –3, A₂=1) — апериодически расходящееся

а) временная диаграмма

б) фазовая диаграмма

Рис. 31. Лабораторная работа №1. Параметры решения: D > 0, , (A₀=1, A₁=3, A₂=1) — апериодически сходящееся

а) временная диаграмма

б) фазовая диаграмма

Рис. 32. Лабораторная работа №1. Параметры решения: D < 0, A₁= 0 (A₀=1, A₁=0, A₂=1) — гармоническое

а) временная диаграмма

б) фазовая диаграмма

Рис. 33. Лабораторная работа №1. Параметры решения: D < 0, (A₀=1, A₁=0.5, A₂=1) — периодическое сходящееся

а) временная диаграмма

б) фазовая диаграмма

Рис. 34. Лабораторная работа №1. Параметры решения: D < 0, (A₀=1, A₁= –0.5, A₂=1) — периодическое расходящееся

а) временная диаграмма

б) фазовая диаграмма

Рис. 35. Лабораторная работа №1. Параметры решения: D = 0, (A₀=1, A₁=2, A₂=1) — сходящееся

а) временная диаграмма

б) фазовая диаграмма

Рис. 36. Лабораторная работа №1. Параметры решения: D = 0, (A₀=1, A₁= –2, A₂=1) — расходящееся

Приложение 2

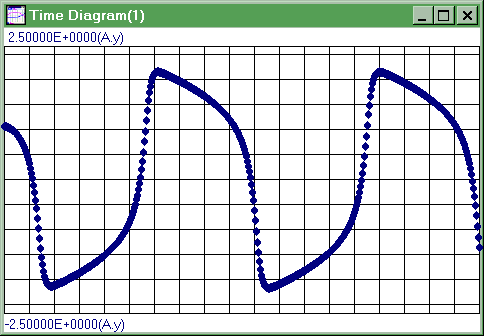
а) временная диаграмма

б) фазовая диаграмма

Рис. 37. Лабораторная работа №2. Параметры решения: действ. корни : , , ( = 3) — неустойчивый узел

а) временная диаграмма

б) фазовая диаграмма

Рис. 38. Лабораторная работа №2. Параметры решения: действ. кор­ни : , , ( = –3) — ассимптотически устойчивый узел

а) временная диаграмма

б) фазовая диаграмма

Рис. 39. Лабораторная работа №2. Параметры решения: действ. кор­ни : , ( = –2) — ассимптотически устойчивый вырожденный узел

а) временная диаграмма

б) фазовая диаграмма

Рис. 40. Лабораторная работа №2. Параметры решения: действ. кор­ни : , ( = 2) — ассимптотически неустойчивый вырожденный узел

а) временная диаграмма

б) фазовая диаграмма

Рис. 41. Лабораторная работа №2. Параметры решения: компл. кор­ни : , ( = –1) — ассимптотически устойчивый фокус

а) временная диаграмма

б) фазовая диаграмма

Рис. 42. Лабораторная работа №2. Параметры решения: компл. кор­ни : , ( = 1) — неустойчивый фокус

а) временная диаграмма

б) фазовая диаграмма

Рис. 43. Лабораторная работа №2. Параметры решения: компл. кор­ни : ( = 0) — устойчивый центр