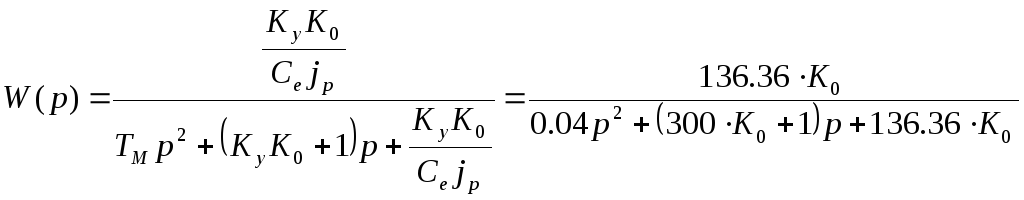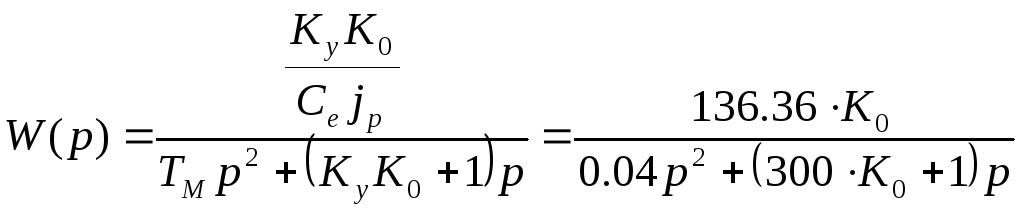лабораторная работа / №2 (4)

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ФИЛИАЛ В Г. ИШИМБАЙ

Отчет по лабораторной работе №2

по предмету «Теория автоматического управления»

на тему: Анализ устойчивости системы автоматического регулирования.

Вариант № 1.

Выполнил: студент гр. АТП-308

Шарипов Д.В.

Приняла: Перевертайло Ю.В.

Ишимбай 2007

1. Цель работы

Приобретение навыков в составлении сложных структурных схем систем автоматического регулирования с помощью пакета прикладных программ, определение ЛАХ и ЛФХ системы. Анализ устойчивости системы по критерию Гурвица-Найквиста, определение границы устойчивости системы.

2. Выполнение работы

Составить на экране дисплея с помощью пакета прикладных программ структурную схему системы автоматического регулирования согласно заданию.

Исходные данные:

Так как звено 1 не удовлетворяет условию физической реализуемости (степень полинома числителя передаточной функции звена превышает степень полинома знаменателя), то необходимо произвести структурные преобразования схемы, а именно перенести узел 2 против направления распространения сигнала через звено 3. Преобразованная структурная схема примет вид:

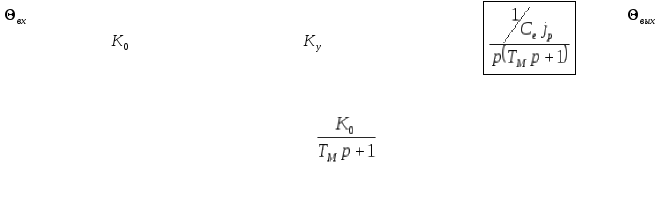
Для составления структурной схемы и моделирования заданной системы воспользуемся пакетом Simulink, входящий в состав пакета MatLab.

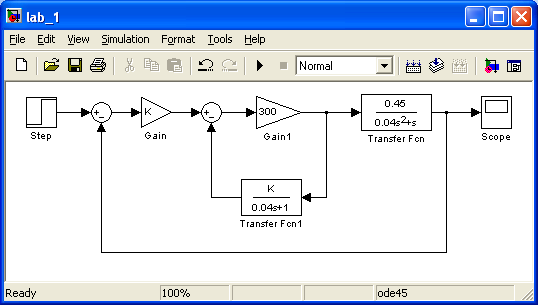
Используя критерий устойчивости Гурвица, определить значение коэффициента передачи K₀ системы, при котором система будет находиться в устойчивом состоянии:

- передаточная функция замкнутой системы

- характеристическое уравнение

Необходимое условие устойчивости () выполняется при .

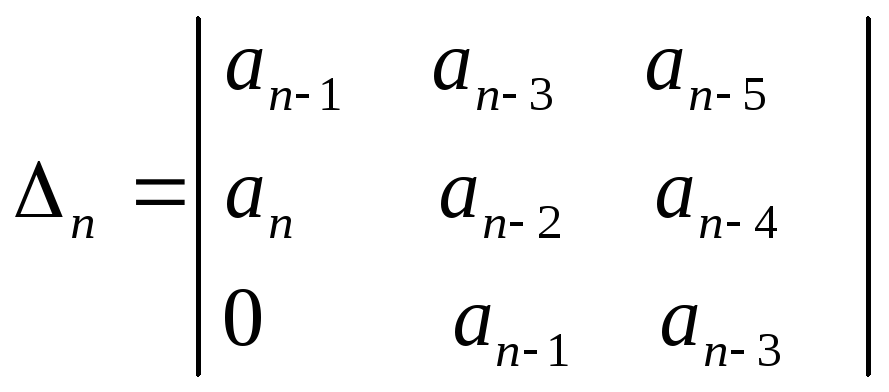- определитель Гурвица

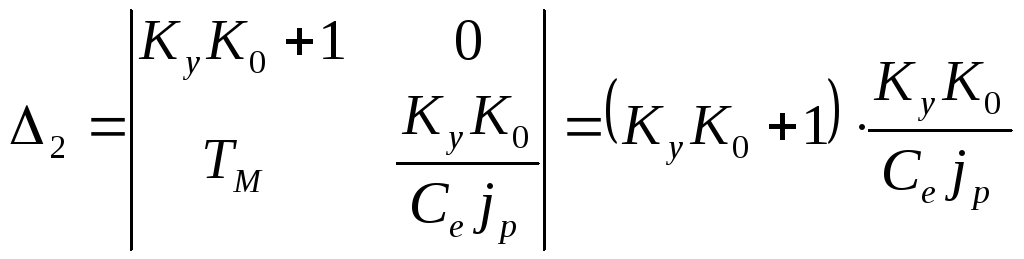- определитель Гурвица для исследуемой системы

- достаточное условие устойчивости для системы второго порядка

Таким образом, при любом положительном значении коэффициента передачи K₀ исследуемая САУ будет находиться в устойчивом состоянии.

Рассчитать с помощью пакета прикладных программ переходные, логарифмические и амплитудно-фазовые характеристики замкнутой и разомкнутой систем автоматического регулирования для трёх режимов работы: неустойчивого, на границе устойчивости, устойчивого, построить все полученные графики.

Так как исследуемая САУ является устойчивой при любом положительном значении коэффициента передачи K₀, то будем рассматривать характеристики только для устойчивого режима.

Замкнутая САУ Передаточная функция:
Переходный процесс
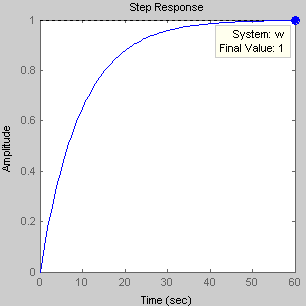
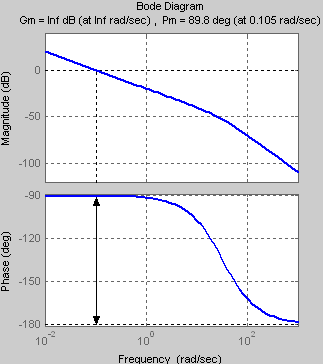
	K0=0.001 Переходная функция h(t) с течением времени стремится к своему установившемуся значению hуст=1. Значит, система находится в устойчивом состоянии.
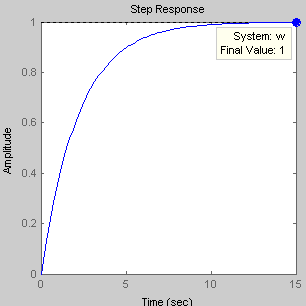
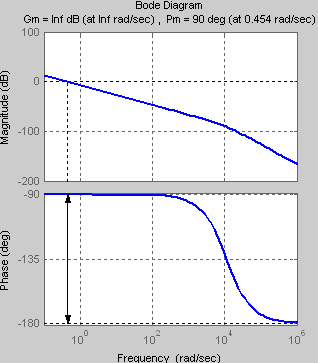
	K0=1.5 Переходная функция h(t) с течением времени стремится к своему установившемуся значению hуст=1. Значит, система находится в устойчивом состоянии.

Разомкнутая САУ Передаточная функция: Логарифмическая амплитудная и фазовая частотные характеристики
ωкр→ ∞ ωср Δφ ΔА→ ∞	K0=0.001 ωср=0.105 ωкр=∞ ωср< ωкр , значит, система находится в устойчивом состоянии. Запас устойчивости по амплитуде: (дБ) Запас устойчивости по фазе: (град)
ωкр→ ∞ ωср Δφ ΔА→ ∞	K0=1.5 ωср=0.454 ωкр=∞ ωср< ωкр , значит, система находится в устойчивом состоянии. Запас устойчивости по амплитуде: (дБ) Запас устойчивости по фазе: (град)

АФЧХ
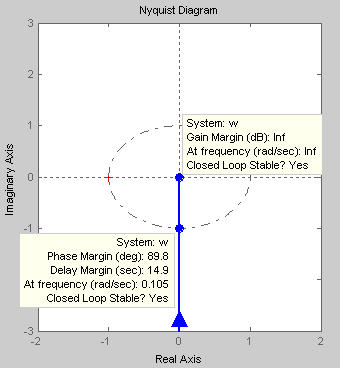
	K0=0.001 Годограф АФЧХ разомкнутой системы не охватывает точку с координатами (-1;j0). Значит, исходя из критерия Найквиста, замкнутая система будет находиться в устойчивом состоянии.
	K0=1.5 Годограф АФЧХ разомкнутой системы не охватывает точку с координатами (-1;j0). Значит, исходя из критерия Найквиста, замкнутая система будет находиться в устойчивом состоянии.

3. Выводы

В лабораторной работе были изучены критерии устойчивости Найквиста и Гурвица, а также оценка устойчивости по логарифмическим частотным характеристикам. С помощью этих критериев была исследована на устойчивость САУ, определили ее границу устойчивости. Результаты критериев полностью совпали. Определили коэффициенты запаса устойчивости по фазе и амплитуде.