лабораторная работа / №1 (2)

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ФИЛИАЛ В Г. ИШИМБАЙ

Кафедра Автоматизации Производственных Процессов

Отчет по лабораторной работе №1

по предмету «Теория автоматического управления»

на тему: Анализ устойчивости нелинейной САУ.

Выполнил: студент гр. АТП-308

Шарипов Д.В.

Принял: Хуснутдинов Д.З.

Ишимбай 2007

1. Цель работы

Изучение метода гармонической линеаризации нелинейных САУ; определение периодических решений и их устойчивости по критерию Гольдфарба; приобретение навыков в составлении сложных структурных схем нелинейных САУ с помощью пакета прикладных программ.

2. Выполнение работы

Задание №4

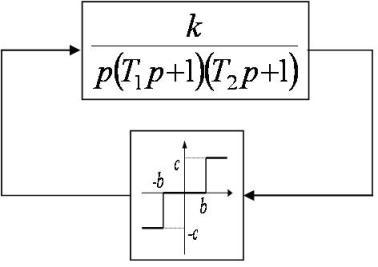
k=4 c^-1; T₁=0.01 c; T₂=0.08 c; b=0.25; c=110

Передаточная функция линейной части имеет вид:

Коэффициенты гармонической линеаризации q(A),q₁(A) для нелинейного элемента (в данном случае это реле с зоной нечувствительности или трехпозиционное реле) имеют вид:

Передаточная функция нелинейного гармонически линеаризованного элемента имеет вид:

Комплексный коэффициент передачи нелинейного линеаризованного элемента имеет вид:

1. Проанализировать устойчивость линейной части системы. Если линейная часть системы неустойчива, добиться её устойчивости при помощи коррекции внутренних свойств.

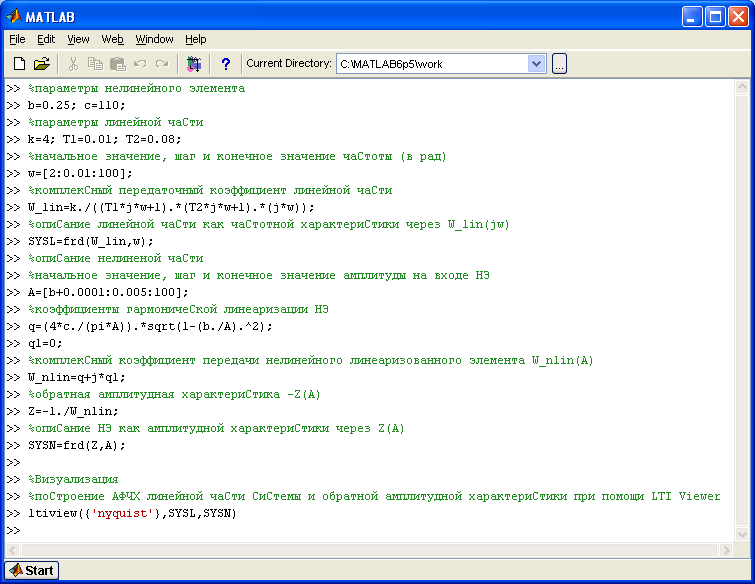
Построим АФЧХ линейной части системы, используя Control System ToolBox пакета MatLab:

Как видно годограф АФЧХ линейной части системы не охватывает точку с координатами

(-1; j0), значит, линейная часть нелинейной САУ является устойчивой.

2. Аналитическим методом определить условия возникновения периодических колебаний в нелинейной замкнутой системе. Определить параметры периодических колебаний (ω₀,A₀).

– передаточная функция замкнутой нелинейной САУ

– характеристическое уравнение

Представив передаточную функцию линейной части в виде , перепишем характеристическое уравнение в виде:

Для возникновения периодических колебаний в системе необходимо, чтобы характеристическое уравнение было равно нулю. Это условие выполняется, если числитель равен нулю:

Заменяя в данном выражении оператор Лапласа p комплексной частотой jω, получим:

Таким образом, условие возникновения периодических колебаний в нелинейной замкнутой САУ имеет вид:

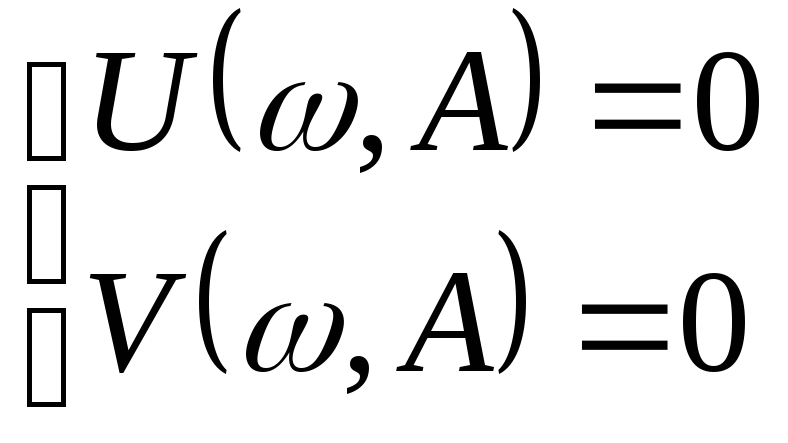
Для заданной нелинейной САУ имеем:

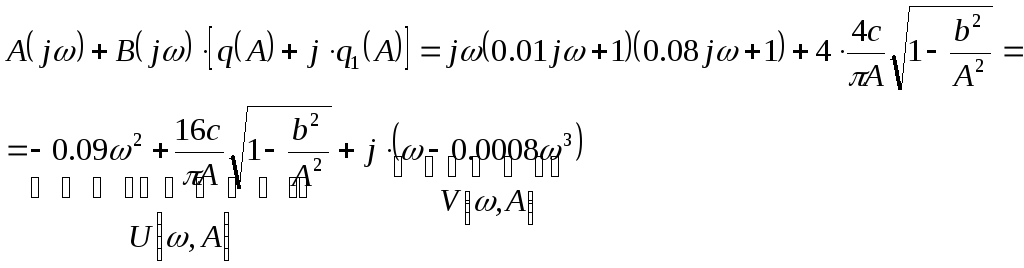
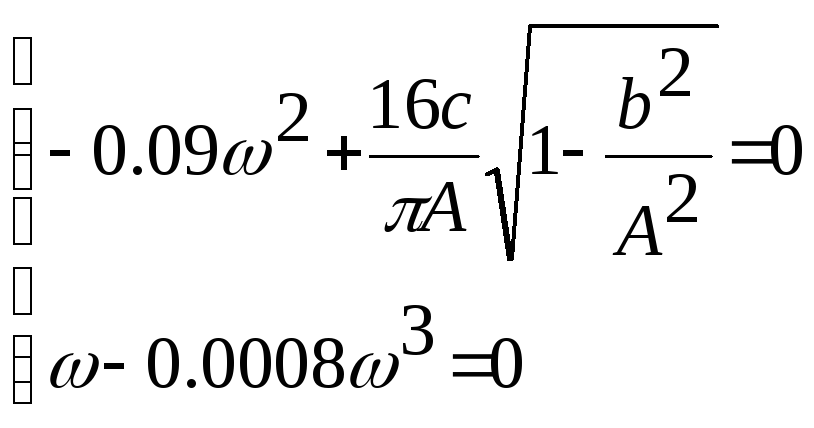
Для решения данной системы уравнений воспользуемся ToolBox Symbolic Math пакета MatLab. Решим второе уравнение системы:

Отбрасывая не положительные решения, получаем с^-1. Подставим данное решение в первое уравнение системы:

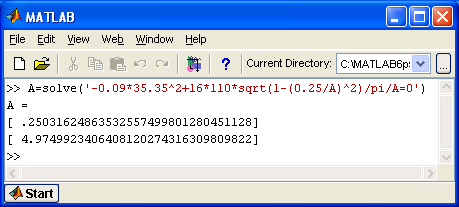
Значит, периодические решения имеют следующие параметры: ω₀=35.35 с^-1 , A₀=0.25 (I)

ω₀=35.35 с^-1 , A₀=4.97 (II)

3. С помощью пакета прикладных программ составить на экране компьютера структурную схему замкнутой нелинейной САУ. В качестве блока задающего воздействия использовать единичную ступенчатую функцию. Получить зависимость выходной величины x_вых(t) и определить по ней параметры (ω₀,A₀).

Для составления структурной схемы и моделирования нелинейной системы воспользуемся пакетом Simulink, входящий в состав пакета MatLab.

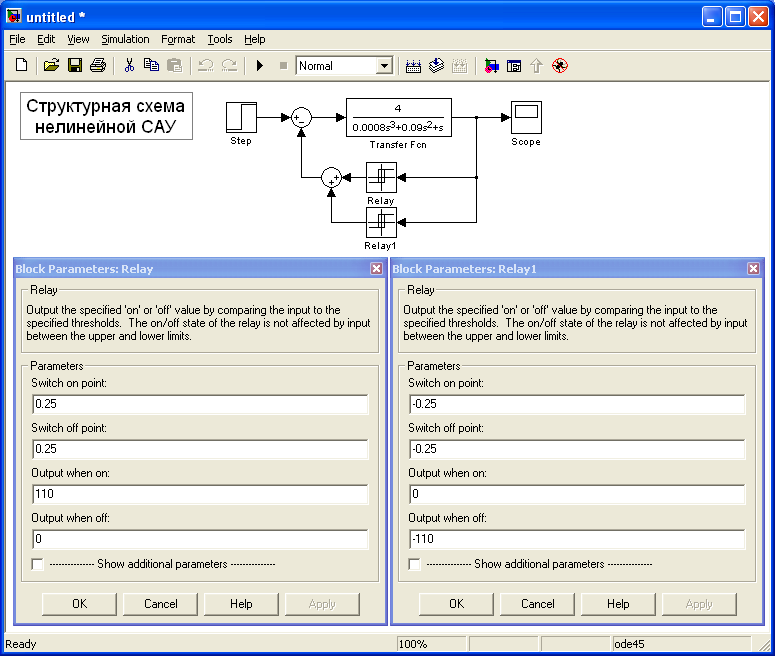
Реле с зоной нечувствительности (трехпозиционное реле) организовано при помощи параллельного соединения двух идеальных двухпозиционных реле (идеальное двухпозиционное реле – это блок Relay с нулевой шириной зоны гистерезиса). Также приведены настройки блоков, входящих в состав реле с зоной нечувствительности.

На выходе устанавливаются периодические колебания x_вых(t):

A₀

T₀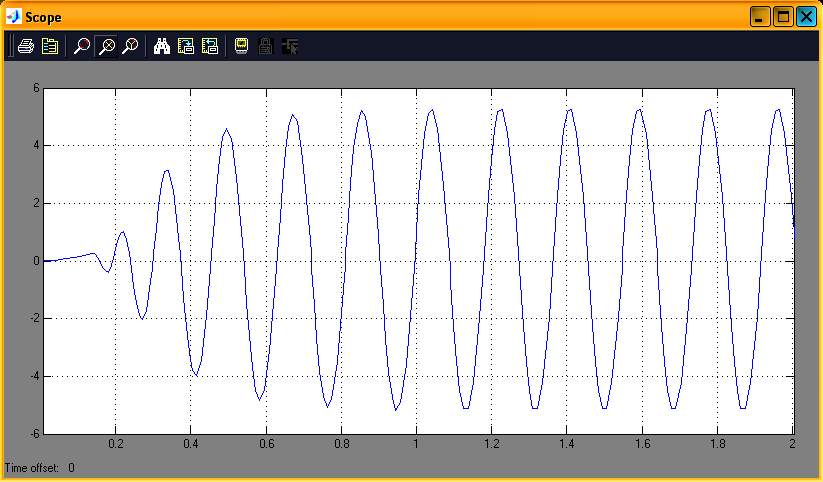

Как видно из графика, амплитуда периодических колебаний равна A₀≈5, а собственная частота колебаний 34.91 с^-1. Данные значения близки ко II группе параметров периодических решений, найденных аналитически. Исходя из того, что физически возможны лишь устойчивые периодические движения, можно сделать вывод, что периодическое решение с параметрами ω₀=35.35 с^-1 , A₀=4.97 является устойчивым решением, а периодическое решение с параметрами ω₀=35.35 с^-1 , A₀=0.25 – неустойчивым.

4. При помощи пакета прикладных программ построить АФЧХ линейной части системы и обратную амплитудную характеристику .

Для построения характеристик и воспользуемся Control System ToolBox пакета MatLab:

Обратная амплитудная характеристика –Z_НЭ(A)

АФЧХ W_ЛИН(jω)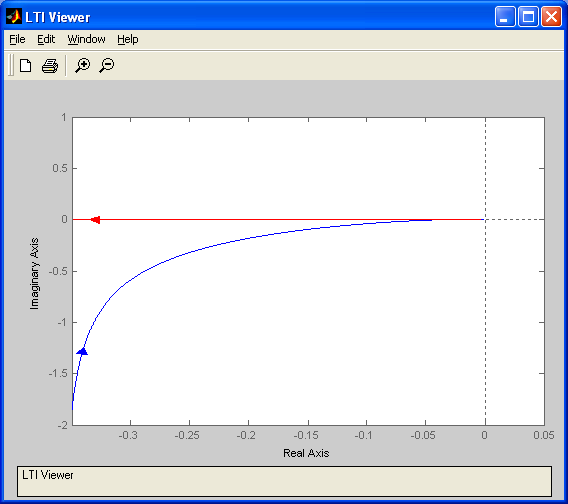

5. Графическим методом определить параметры периодических колебаний (ω₀,A₀ ), а также указать точки с устойчивым (автоколебания) и неустойчивым периодическим решением.

Обратная амплитудная характеристика –Z_НЭ(A)

АФЧХ W_ЛИН(jω)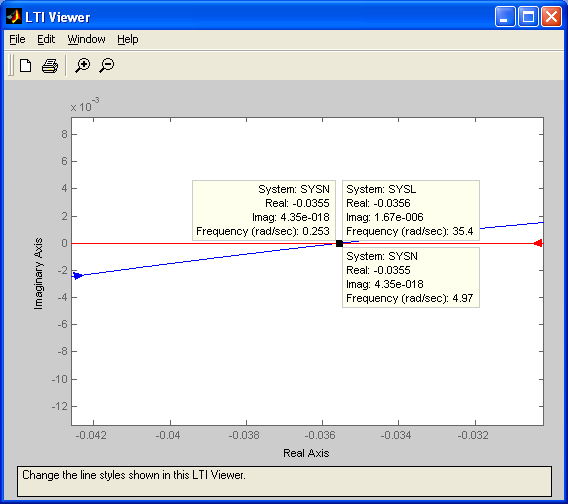

Так как , то обратная амплитудная характеристика вся укладывается на отрицательной части вещественной оси.

При A=b значение комплексного коэффициента передачи нелинейного линеаризованного элемента

равно нулю. Это значит, что при A=0.25 обратная амплитудная характеристика стремится к -∞. При дальнейшем увеличении A, происходит увеличение значения комплексного коэффициента передачи , соответственно уменьшение значения , следовательно, увеличение значения обратной амплитудной характеристики . Комплексный коэффициент передачи нелинейного линеаризованного элемента достигает своего максимума при A=, а при дальнейшем увеличении A происходит уменьшение его значения (при A→∞ →0). Значит, обратная амплитудная характеристика также, достигнув своего максимума, стремится обратно к -∞. Вышесказанное можно пояснить следующим рисунком:

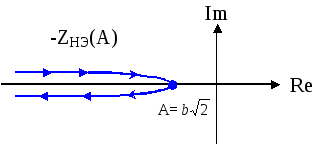
Этот рисунок является схематичным, так как обратная амплитудная характеристика , как было отмечено выше, полностью лежит на отрицательной части вещественной оси. Данное пояснение было дано, чтобы показать, что графики АФЧХ линейной части и обратной амплитудной характеристики пересекаются в двух точках. Данные точки совпадают, значения частоты в них, определяемой по АФЧХ линейной части , одинаковы, но значения амплитуды, определяемые по обратной амплитудной характеристики , различны.

Из графика находим, что первая точка пересечения имеет параметры A₀≈0.253 ω₀=35.4 с^-1, а вторая точка имеет параметры A₀≈4.97 ω₀=35.4 с^-1.

Исходя из критерия устойчивости периодических решений, получаем, что первая точка пересечения с параметрами A₀≈0.253 ω₀=35.4 с^-1 дает неустойчивое периодическое решение, а вторая точка с параметрами A₀≈4.97 ω₀=35.4 с^-1 дает устойчивое периодическое решение (автоколебания) периодическое решение ()получаем, что ыдаютом:

етрами:

нулю.000000000000000000000000000000000000000000000000000000000.

6. Сравнить расчетные результаты с полученными при моделировании. Сделать вывод.

Результаты, полученные при моделировании, а также графическим способом, близки к расчетным результатам, полученным аналитически.

3. Вывод

В данной работе был изучен метода гармонической линеаризации нелинейных САУ; определили периодические решения, а также исследовали их на устойчивость, используя критерий Гольдфарба; были приобретены навыки в составлении сложных структурных схем нелинейных САУ с помощью пакета прикладных программ. Результаты, полученные при моделировании, а также графическим способом, близки к расчетным результатам, полученным аналитически.