
лабораторная работа / laboratornaya_rabota_postroenie_chastotnyh_harakteristik_met
.docxЗадание 1. Построение частотных характеристик методом типовых звеньев.
Дано:
 .
.
Решение:
Коэффициент
передачи САУ:
 ,86.
,86.
Найдем корни полиномов числителя и знаменателя передаточной функции, для этого воспользуемся программой MatLab.
w=tf([1250 1250 20200 4000],[967.68 1330.56 725.76 28])
Transfer function:
1250 s^3 + 1250 s^2 + 20200 s + 4000
------------------------------------
967.7 s^3 + 1331 s^2 + 725.8 s + 28
zero(w)
ans =
-0.4000 + 3.9799i
-0.4000 - 3.9799i
-0.2000
pole(w)
ans =
-0.6667 + 0.5000i
-0.6667 - 0.5000i
-0.0417
Получаем:
 ,
,
 ,
,
 ,
,
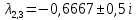 .
.
В
соответствии с видом полученных корней
разобьем передаточную функцию САУ на
типовые звенья.
Так как полином числителя передаточной
функции имеет один действительный
отрицательный корень, и пару
комплексно-сопряженных корней с
отрицательными вещественными частями,
то его можно представить в виде
произведения двух типовых звеньев:
одного идеально дифференцирующего
звена первого порядка с постоянной
времени
 ,
и одного реально дифференцирующего
звена второго порядка с постоянной
времени
,
и одного реально дифференцирующего
звена второго порядка с постоянной
времени
 ,
декрементом
затухания
,
декрементом
затухания
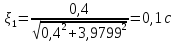 .
.
Полином
знаменателя передаточной
функции имеет один действительный
отрицательный корень, и пару
комплексно-сопряженных корней с
отрицательными вещественными частями,
то его можно представить в виде
произведения двух типовых звеньев:
одного апериодического звена с постоянной
времени
 ,
и одного колебательного
звена с постоянной времени
,
и одного колебательного
звена с постоянной времени
 ,
декрементом
затухания
,
декрементом
затухания
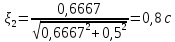 .
.
Таким образом, передаточная функция САУ имеет вид:



На частоте
 строим опорную точку с ординатой
строим опорную точку с ординатой

 ,
а на ось частот наносим частоты сопряжения
асимптотических ЛАХ звеньев:
,
а на ось частот наносим частоты сопряжения
асимптотических ЛАХ звеньев:
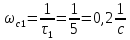 ,
,
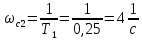 ,
,
 ,
,
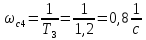 .
.
Так как передаточная функция не содержит ни одно интегрирующего звена и ни одного идеально усилительного звена то, через опорную точку проводим низкочастотную асимптоту ЛАХ с наклоном 0 дБ/дек.
Наименьшая
частота сопряжения
 принадлежит апериодическому
звену,
поэтому
на этой частоте изменяем наклон
низкочастотной асимптоты на величину
наклона наклонной асимптоты апериодического
звена -20 дБ/дек. Асимптоту с измененным
наклоном проводим до следующей (по мере
возрастания) частоте сопряжения (ωс1).
Она принадлежит: идеально дифференцирующему
звену первого порядка, поэтому на этой
частоте наклон асимптоты изменяем на
+20 дБ/дек. Асимптоту с измененным наклоном
проводим до следующей (по мере возрастания)
частоте сопряжения (ωс4).
Она принадлежит колебательному
звену, поэтому на этой частоте наклон
асимптоты изменяем на -40 дБ/дек. Затем
продолжаем асимптоту до последней
частоты сопряжения (ωс2).
Эта частота принадлежит реально
дифференцирующему
звену второго порядка, соответственно
величину наклона асимптоты изменяем
на +40 дБ/дек.
принадлежит апериодическому
звену,
поэтому
на этой частоте изменяем наклон
низкочастотной асимптоты на величину
наклона наклонной асимптоты апериодического
звена -20 дБ/дек. Асимптоту с измененным
наклоном проводим до следующей (по мере
возрастания) частоте сопряжения (ωс1).
Она принадлежит: идеально дифференцирующему
звену первого порядка, поэтому на этой
частоте наклон асимптоты изменяем на
+20 дБ/дек. Асимптоту с измененным наклоном
проводим до следующей (по мере возрастания)
частоте сопряжения (ωс4).
Она принадлежит колебательному
звену, поэтому на этой частоте наклон
асимптоты изменяем на -40 дБ/дек. Затем
продолжаем асимптоту до последней
частоты сопряжения (ωс2).
Эта частота принадлежит реально
дифференцирующему
звену второго порядка, соответственно
величину наклона асимптоты изменяем
на +40 дБ/дек.
Строим график ЛФХ
звеньев. Суммируем алгебраические
ординаты точек этих графиков, лежащих
на одной частоте, получаем график ЛФХ
звеньев.
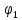 - график апериодического
звена,
- график апериодического
звена,
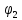 - график
идеально дифференцирующего звена
первого порядка,
- график
идеально дифференцирующего звена
первого порядка,
 - график
колебательного звена,
- график
колебательного звена,
 - график
дифференцирующего звена второго порядка.
- график
дифференцирующего звена второго порядка.
Задание 1. Решение с помощью MatLab.
w=tf([1250 1250 20200 4000],[967.68 1330.56 725.76 28])
Transfer function:
1250 s^3 + 1250 s^2 + 20200 s + 4000
------------------------------------
967.7 s^3 + 1331 s^2 + 725.8 s + 28
zero(w)
ans =
-0.4000 + 3.9799i
-0.4000 - 3.9799i
-0.2000
pole(w)
ans =
-0.6667 + 0.5000i
-0.6667 - 0.5000i
-0.0417
zpk([-0.2000 -0.4000+3.9799i -0.4000-3.9799i],[-0.0417 -0.6667+0.5000i -0.6667-0.5000i],142.86)
Zero/pole/gain:
142.86 (s+0.2) (s^2 + 0.8s + 16)
----------------------------------
(s+0.0417) (s^2 + 1.333s + 0.6945)
bode(w), grid

Задание 2. Построение частотных характеристик методом типовых звеньев.
Дано:
 .
.
Решение:
Коэффициент
передачи САУ:
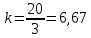 .
.
Найдем корни полиномов числителя и знаменателя передаточной функции, для этого воспользуемся программой MatLab.
w=tf([40.5 406.8 20 20],[240 333.6 44.4 3 0])
Transfer function:
40.5 s^3 + 406.8 s^2 + 20 s + 20
------------------------------------
240 s^4 + 333.6 s^3 + 44.4 s^2 + 3 s
zero(w)
ans =
-10.0000
-0.0222 + 0.2211i
-0.0222 - 0.2211i
pole(w)
ans =
0
-1.2500
-0.0700 + 0.0714i
-0.0700 - 0.0714i
Получаем:
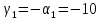 ,
,
 ,
,
 ,
,
 ,
,
 .
.
В
соответствии с видом полученных корней
разобьем передаточную функцию САУ на
типовые звенья.
Так как полином числителя передаточной
функции имеет один действительный
отрицательный корень, и пару
комплексно-сопряженных корней с
отрицательными вещественными частями,
то его можно представить в виде
произведения двух типовых звеньев:
одного идеально дифференцирующего
звена первого порядка с постоянной
времени
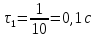 ,
и одного реально дифференцирующего
звена второго порядка с постоянной
времени
,
и одного реально дифференцирующего
звена второго порядка с постоянной
времени
 ,
декрементом
затухания
,
декрементом
затухания
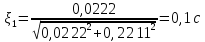 .
.
Полином
знаменателя передаточной
функции имеет один нулевой корень, один
действительный отрицательный корень,
и пару комплексно-сопряженных корней
с отрицательными вещественными частями,
то его можно представить в виде
произведения трех типовых звеньев: одно
интегрирующего звена, одного апериодического
звена с постоянной времени
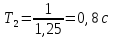 ,
и одного колебательного звена
с постоянной времени
,
и одного колебательного звена
с постоянной времени
 ,
декрементом
затухания
,
декрементом
затухания
 .
.
Таким образом, передаточная функция САУ имеет вид:
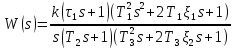


На частоте
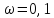 строим опорную точку с ординатой
строим опорную точку с ординатой

 ,
а на ось частот наносим частоты сопряжения
асимптотических ЛАХ звеньев:
,
а на ось частот наносим частоты сопряжения
асимптотических ЛАХ звеньев:
 ,
,
 ,
,
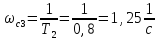 ,
,
 .
.
Так как передаточная функция содержит одно интегрирующее звено то, через опорную точку с ординатой 20lgk=20lg6,67=16,5 дБ, проводим низкочастотную асимптоту ЛАХ с наклоном -20 дБ/дек.
Наименьшая
частота сопряжения
 принадлежит колебательному
звену,
поэтому
на этой частоте изменяем наклон
низкочастотной асимптоты на величину
наклона наклонной асимптоты колебательного
звена -40
дБ/дек. Асимптоту с измененным наклоном
проводим до следующей (по мере возрастания)
частоте сопряжения (ωс2).
Она принадлежит дифференцирующему
звену второго порядка, поэтому на этой
частоте наклон асимптоты изменяем на
+40 дБ/дек. Асимптоту с измененным наклоном
проводим до следующей (по мере возрастания)
частоте сопряжения (ωс3).
Она принадлежит апериодическому звену,
поэтому на этой частоте наклон асимптоты
изменяем на -20 дБ/дек. Затем продолжаем
асимптоту до последней частоты сопряжения
(ωс1).
Эта частота принадлежит дифференцирующему
звену первого порядка, соответственно
величину наклона асимптоты изменяем
на +20 дБ/дек.
принадлежит колебательному
звену,
поэтому
на этой частоте изменяем наклон
низкочастотной асимптоты на величину
наклона наклонной асимптоты колебательного
звена -40
дБ/дек. Асимптоту с измененным наклоном
проводим до следующей (по мере возрастания)
частоте сопряжения (ωс2).
Она принадлежит дифференцирующему
звену второго порядка, поэтому на этой
частоте наклон асимптоты изменяем на
+40 дБ/дек. Асимптоту с измененным наклоном
проводим до следующей (по мере возрастания)
частоте сопряжения (ωс3).
Она принадлежит апериодическому звену,
поэтому на этой частоте наклон асимптоты
изменяем на -20 дБ/дек. Затем продолжаем
асимптоту до последней частоты сопряжения
(ωс1).
Эта частота принадлежит дифференцирующему
звену первого порядка, соответственно
величину наклона асимптоты изменяем
на +20 дБ/дек.
Строим график ЛФХ
звеньев. Суммируем алгебраические
ординаты точек этих графиков, лежащих
на одной частоте, получаем график ЛФХ
звеньев.
 - график
колебательного звена,
- график
колебательного звена,
 – график
дифференцирующего звена второго порядка
,
– график
дифференцирующего звена второго порядка
,
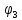 - график
апериодического звена,
- график
апериодического звена,
 - график
идеально дифференцирующего звена
первого порядка.
- график
идеально дифференцирующего звена
первого порядка.
Задание 2. Решение с помощью MatLab.
w=tf([40.5 406.8 20 20],[240 333.6 44.4 3 0])
Transfer function:
40.5 s^3 + 406.8 s^2 + 20 s + 20
------------------------------------
240 s^4 + 333.6 s^3 + 44.4 s^2 + 3 s
zero(w)
ans =
-10.0000
-0.0222 + 0.2211i
-0.0222 - 0.2211i
pole(w)
ans =
0
-1.2500
-0.0700 + 0.0714i
-0.0700 - 0.0714i
zpk([-10 -0.0222+0.2211i -0.0222-0.2211i],[0 -1.25 -0.07+0.0714i -0.07-0.0714i],6.67)
Zero/pole/gain:
6.67 (s+10) (s^2 + 0.0444s + 0.04938)
-------------------------------------
s (s+1.25) (s^2 + 0.14s + 0.009998)
bode(w),grid

