
лабораторная работа / laboratornaya_rabota_po_tau_poluchenie_i_issledovanie_dinami
.docФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Факультет автоматики и информационных технологий
Кафедра «Автоматика и управление в технических системах»
ОТЧЕТ
Лабораторная работа №1
Получение и исследование динамических и частотных характеристик
типовых динамических звеньев.
Вариант №2
Выполнила: ххххххххххххххх
ххххххххххххххх
Проверил: Мандра А. Г.
Плешивцева Ю.Э.
Самара 2009г.
Лабораторная работа №1
-
Получение и исследование динамических и частотных характеристик типовых динамических звеньев.
Цель работы: Исследовать динамические и частотные характеристики типовых динамических звеньев систем автоматического регулирования. Изучить зависимость характеристик звеньев от параметров системы.
-
Задание
Для идеального трансформатора записать передаточную функцию (по входу – напряжение первичной обмотки, по выходу – напряжение вторичной обмотки) при заданном числе витков первичной и вторичной обмотки. Определить переходную и частотные характеристики. (АФХ, ЛАЧХ, ЛФЧХ).
Работа трансформатора основана на двух базовых принципах:
-
Изменяющийся во времени электрический ток создает магнитное поле (электромагнетизм);
-
Изменение магнитного потока, проходящего через обмотку, создает ЭДС в этой обмотке (электромагнитная индукция).
Схематично, процесс преобразования можно изобразить следующим образом:
![]() . (1.1)
. (1.1)
ЭДС, создаваемая во вторичной обмотке, может быть вычислена по закону Фарадея, который гласит, что:
![]() . (1.2)
. (1.2)
ЭДС, создаваемая в первичной обмотке, соответственно:
![]() . (1.3)
. (1.3)
Поделив уравнение (1.2) на (1.3), получим соотношение:
![]() ,
(1.4)
,
(1.4)
![]() .
(1.5)
.
(1.5)
Соединив уравнения (1.4) и (1.5), получим уравнение идеального трансформатора:
![]() . (1.6)
. (1.6)
![]() ,
отсюда
,
отсюда
![]()
Функциональная схема выглядит так:
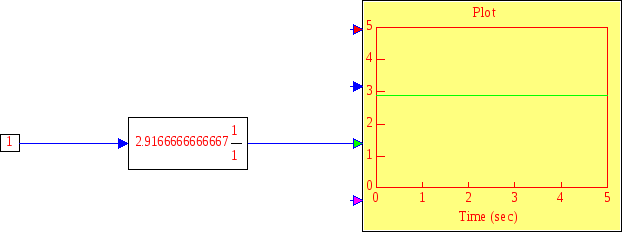
Рис. 1 Функциональная схема
Переходные и частотные характеристики (АФХ, ЛАЧХ, ЛФЧХ).
A(ω) = k, φ(ω) = arctg(0) = 0; L(ω) = 20lg(k);
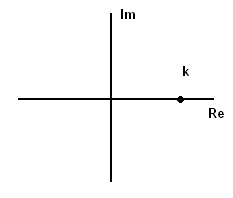

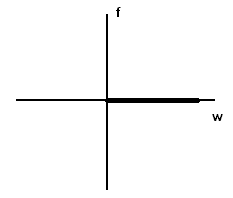
Рис. 2 а) АФХ б) ЛАЧХ в) ЛФЧХ
Контрольные вопросы к заданию:
-
На сколько дБ изменится значение ЛАЧХ, если увеличить число витков во вторичной обмотке в 10 раз? Увеличить число витков в первичной обмотке в 2 раза? Как влияет значение параметра k на фазовую характеристику?
![]() дБ;
дБ;
![]() дБ
дБ
Влияет на положение точки k в зависимости от значения коэффициента k;
-
Чему равен коэффициент передачи k, если значение ЛАЧХ равно 20 дБ?
![]()
-
Задание
Для модели бака записать передаточную функцию (вход – расход наполнения бака, выход - уровень). Принять, что расход из бака равен нулю. Построить переходную и частотные характеристики (АФХ, ЛАЧХ, ЛФЧХ).
Уровень воды в баке контролируется кранами на входе и выходе, которые открываются мгновенно и скорость входного и выходного потоков воды определяются как (м куб/час):
![]() ,
(2.1)
,
(2.1)
![]() . (2.2)
. (2.2)
Объем воды в баке:
![]() .
(2.3)
.
(2.3)
Преобразование Лапласа выражений (2.1) и (2.3) даст:
![]() , (2.4)
, (2.4)
![]() .
(2.5)
.
(2.5)
В данном
случае
![]() ,
тогда подставим (2.4) в (2.5), получим:
,
тогда подставим (2.4) в (2.5), получим:
![]() .
(2.6)
.
(2.6)
Получим передаточную функцию бака, входом которой является расход наполнения, выходом – уровень:
![]() ,
(2.7)
,
(2.7)
где D
= 0,64*2=1.28
![]()
h(t) = k*t
Функциональная схема выглядит так:

Рис. 3 Функциональная схема
Переходные и частотные характеристики (АФХ, ЛАЧХ, ЛФЧХ).
![]() ;
;

Рис. 4 а) АФХ б) ЛАЧХ в) ЛФЧХ
Контрольные вопросы к заданию:
-
Чему равно значение переходной характеристики при t = 1c?
h(1) = k = 0,124;
-
Чему равны значения ЛАЧХ и ЛФЧХ на частоте
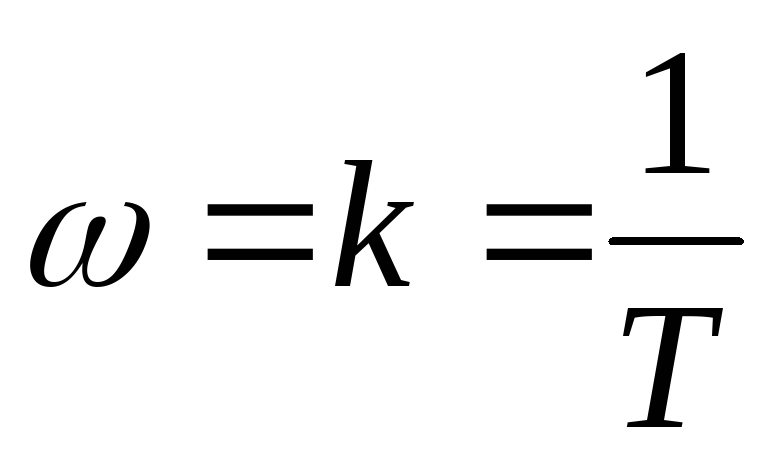 ?
?
 ;
;
-
Как изменится переходная характеристика и ЛАЧХ при увеличении радиуса основания в два раза?
При увеличении радиуса основания в 2 раза, Tб увеличиться в четыре раза и коэффициент k = 1/T уменьшиться в 4 раза;
-
Чему равна постоянная времени Т, если
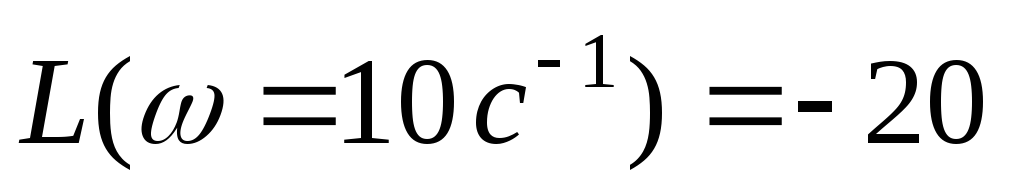 дБ?
дБ?
![]()
-
Задание
Для RC – фильтра записать передаточную функцию (вход – напряжение , выход – напряжение ). Определить переходную и частотные характеристики (АФХ, ЛАЧХ, ЛФЧХ).
Передаточная функция RC – фильтра определяется следующим образом:
![]() ,
(3.1)
,
(3.1)
где R = 250*2=500 Ом; С = 17*2=34 мкФ
h(t) = 0,017*(1 – exp(-t/0,017))
Функциональная схема выглядит так:

Рис. 5 Функциональная схема
Переходные и частотные характеристики (АФХ, ЛАЧХ, ЛФЧХ).
![]()
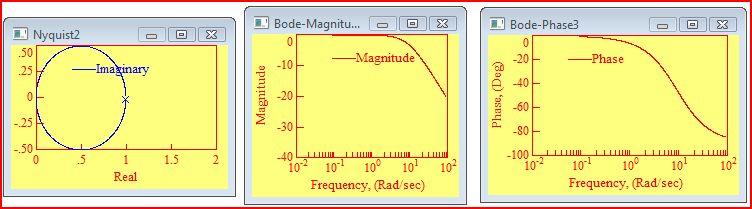
Рис. 6 а) АФХ б) ЛАЧХ в) ЛФЧХ
Контрольные вопросы к заданию:
-
Ч
 ему
равны значения ЛАЧХ и ЛФЧХ на частотах
ему
равны значения ЛАЧХ и ЛФЧХ на частотах
 ?
?
![]()
-
Как отражается на переходной и частотных характеристиках уменьшение (увеличение) сопротивления резистора в 4 раза?
![]()
-
Чему равно значение постоянной времени Т, при котором для
 значение
значение
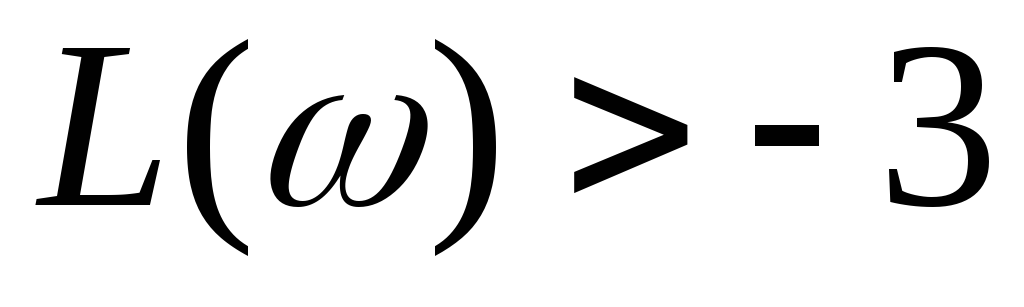 дБ,
а значение
дБ,
а значение
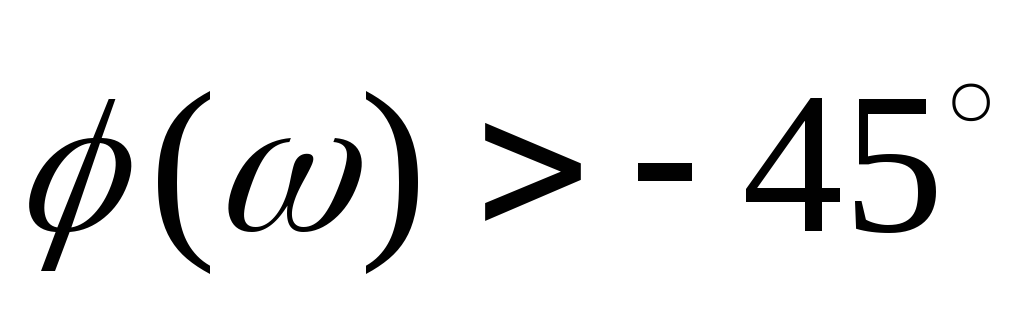 ,
если коэффициент передачи К = 1?
,
если коэффициент передачи К = 1?
При R1 = 4*R, на ЛАЧХ точка частоты сопряжения смещается влево, а предел переходной характеристики увеличивается;
-
Как измениться передаточная функция, если записать ее для потоков?
При уменьшении в 4 раза R на ЛАЧХ точка частоты сопряжения смещается вправо, а предел переходной характеристики уменьшается.
-
Задание
Для неустойчивых апериодических звеньев с ПФ вида
![]() (4.1)
(4.1)
Провести исследования в условиях задачи 1.3, ответить на поставленные в этой задачи вопросы. Сравнить характеристики каждого из звеньев с характеристиками устойчивого апериодического звена первого порядка, а также положение полюсов на комплексной плоскости.
![]() ,
(4.2)
,
(4.2)
![]() ,
(4.3)
,
(4.3)
где k = 8*2=16; Т = 0,2*2=0,4.
Функциональная схема первого апериодического звена выглядит так:
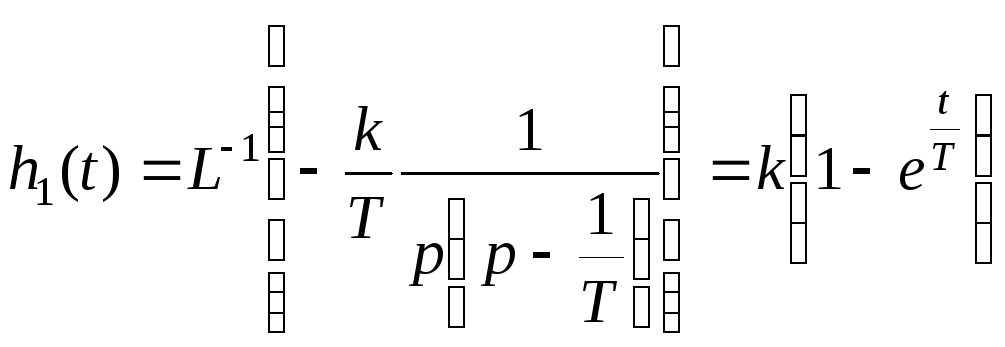

Рис. 7 Функциональная схема
Переходные и частотные характеристики первого апериодического звена (АФХ, ЛАЧХ, ЛФЧХ).


Рис. 8 а) АФХ б) ЛАЧХ в) ЛФЧХ
Функциональная схема второго апериодического звена выглядит так:


Рис. 9 Функциональная схема
Переходные и частотные характеристики второго апериодического звена (АФХ, ЛАЧХ, ЛФЧХ).

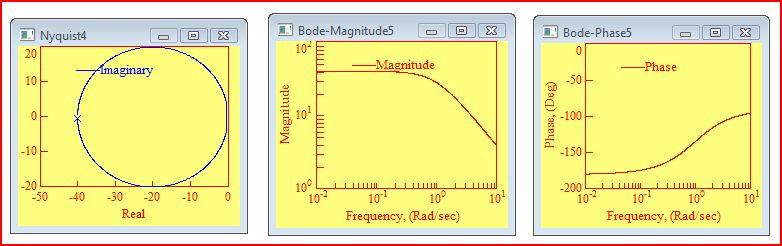
Рис. 10 а) АФХ б) ЛАЧХ в) ЛФЧХ
-
Задание
Для системы «вода-пробка» записать передаточную функцию (вход – задания, выход – глубина погружения) при учете сопротивления воды и без.
Определить
переходную и частотные характеристики
(АФХ, ЛАЧХ и ЛФЧХ) при различных значениях
высоты пробки, плотности жидкости
(рассмотреть спирт, глицерин при
температуре 25![]() С).
Провести исследование характеристик
звена.
С).
Провести исследование характеристик
звена.
Без учета силы сопротивления:

C учетом силы сопротивления:
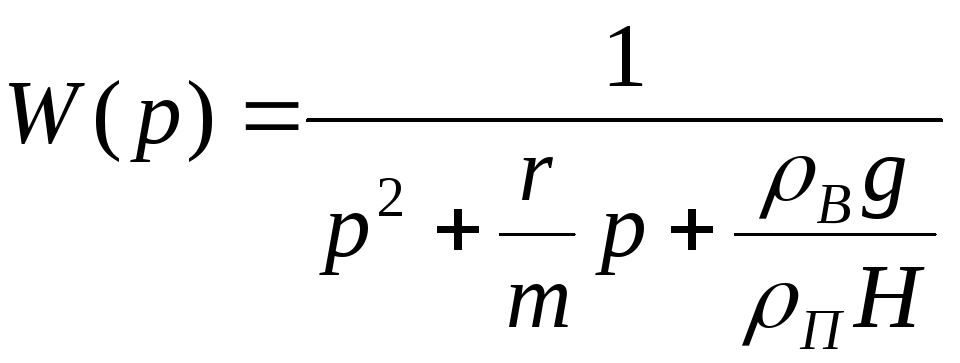
где
![]()
![]() ;
;![]()
Функциональная схема второго апериодического звена выглядит так:
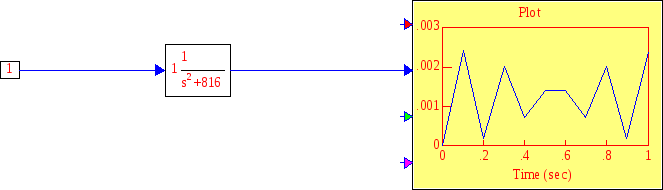

Рис. 11 Функциональные схемы в 2-х случаях
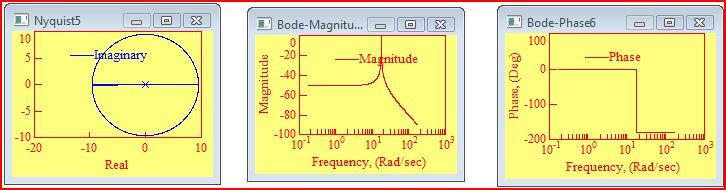
Рис. 10 а) АФХ б) ЛАЧХ в) ЛФЧХ – для первого случая

Рис. 10 а) АФХ б) ЛАЧХ в) ЛФЧХ – для второго случая
-
Задание
Определить:
а) коэффициент усиления К и постоянную
времени Т апериодического звена первого
порядка![]() б) постоянную интегрирования Т
интегрируещего звена
б) постоянную интегрирования Т
интегрируещего звена
![]() ;
при заданном значении входного сигнала
и по графику переходной функции.
;
при заданном значении входного сигнала
и по графику переходной функции.
а)
![]()
![]() ,
если
,
если
![]() ;
;
![]() ;
;
![]()
![]() ;
; ![]() ,
,
![]()
![]() ;
; ![]() ,
,
![]()

Рис. 11 Переходный процесс апериодического звена первого порядка
б)
![]()
![]()
![]()
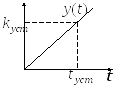
Рис. 11 Переходный процесс интегрирующего звена
-
Задание
Аналитически определить время окончания переходного процесса для передаточной функции апериодического звена первого порядка.
![]()
![]() ;
; ![]() ,
,
![]()
-
Задание
Вывести аналитически частотные характеристики для передаточной функции:
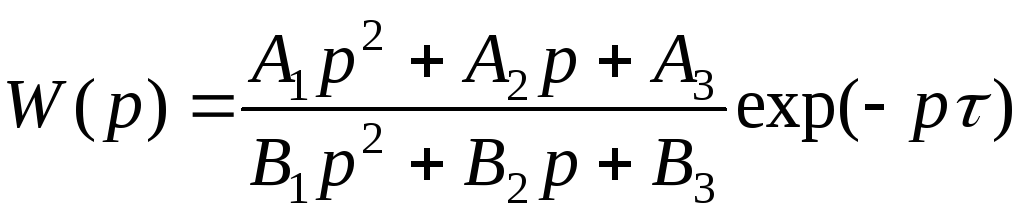

![]()

Для удобства в вычислениях подставим числа:

Пусть
![]() ,
,
![]() ,
тогда
,
тогда
![]()
![]()

![]()
![]()
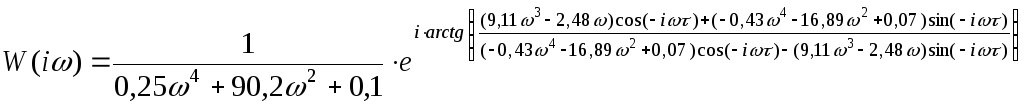
![]()
