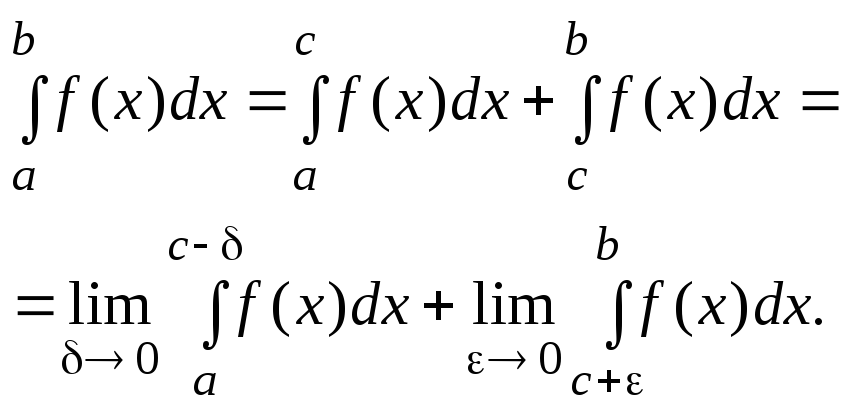- •Раздел 6 основы интегрального исчисления
- •Глава 12. Неопределенный интеграл
- •12.1. Понятие первообразной функции. Неопределенный интеграл
- •12.2. Свойства неопределенного интеграла
- •12.3. Таблица интегралов
- •12.4. Методы интегрирования
- •Метод разложения
- •Замена переменной интегрирования
- •Интегрирование по частям
- •12.5. Интегрирование рациональных дробей
- •12.6. Интегрирование некоторых видов иррациональностей
- •Глава 12
- •Глава 13. Определенный интеграл
- •13.1. Понятие определенного интеграла
- •13.2. Формула Ньютона — Лейбница
- •13.3. Свойства определенного интеграла
- •13.4. Замена переменной под знаком определенного интеграла
- •13.5. Интегрирование по частям в определенном интеграле
- •13.6. Приложения определенного интеграла
- •Глава 13
- •Глава 14. Несобственные интегралы
- •14.1. Несобственные интегралы I рода
- •14.2. Несобственные интегралы II рода
- •Глава 14
14.2. Несобственные интегралы II рода
Пусть функция
![]() непрерывна
при
непрерывна
при
![]() и имеет точку разрыва при
и имеет точку разрыва при
![]() .
Тогда несобственный интеграл определяется
формулой
.
Тогда несобственный интеграл определяется
формулой
|
|
(14.4) |
и называется несобственным интегралом II рода.
Если предел в правой части равенства существует и конечен, то интеграл называется сходящимся, в противном случае – расходящимся.
Пример
14.3. Найти
![]() .
.
![]()
Это означает, что
полубесконечная фигура, ограниченная
осями координат, кривой
![]() и прямой
и прямой
![]() имеет конечную площадь, равную 2 ед2
(см. рис. 14.3).
имеет конечную площадь, равную 2 ед2
(см. рис. 14.3).

Рис. 14.3
Аналогично
определяется несобственный интеграл,
имеющий точку разрыва
![]() :
:
|
|
(14.5) |
Пример
14.4. Найти
![]() .
.

Если функция имеет
разрыв в т.![]() ,
то эта точка разбивает отрезок
интегрирования на два отрезка, и
несобственный интеграл равен
,
то эта точка разбивает отрезок
интегрирования на два отрезка, и
несобственный интеграл равен
|
|
(14.6) |
Замечание.
Несобственный интеграл II
рода
![]() сходится, если сходится каждый интеграл
в правой части равенства (14.6).
сходится, если сходится каждый интеграл
в правой части равенства (14.6).
УПРАЖНЕНИЯ
Вычислить несобственный интеграл
14.5.
![]() 14.6.
14.6.
![]() 14.7.
14.7.
![]() 14.8.
14.8.
![]()
14.9.
![]() 14.10.
14.10.
![]() 14.11.
14.11.
![]()
14.12.
![]() 14.13.
14.13.
![]() 14.14.
14.14.
![]()
14.15.
![]() 14.16.
14.16.
![]() 14.17.
14.17.
![]()
14.18.
![]() 14.19.
14.19.
![]() 14.20.
14.20.

14.21.
 14.22.
14.22.
![]() 14.23.
14.23.
![]()
14.24.
![]()
О Т В Е Т Ы К У П Р А Ж Н Е Н И Я М
Глава 14
14.5.
1. 14.6. Интеграл расходится. 14.7.
![]() 14.8.
14.8.
![]() 14.9.
14.9.
![]() 4.10.
4.10.
![]() 14.11.
14.11.
![]() 14.12.
14.12.
![]() 14.13.
14.13.
![]() 14.14.
14.14.
![]()
14.15.
![]() 14.16.
14.16.
![]() 14.17. 1. 14.18. 16. 14.19. Интеграл
расходится. 14.20. 6. 14.21.
14.17. 1. 14.18. 16. 14.19. Интеграл
расходится. 14.20. 6. 14.21.
![]() 14.22.
14.22.
![]() 14.23. Интеграл расходится.
14.23. Интеграл расходится.
14.24. 1.