
- •Раздел 5 основы дифференциального исчисления
- •Глава 9. Производная функции
- •9.1. Определение производной.
- •9.2. Связь между непрерывностью и существованием производной
- •9.3. Таблица производных
- •9.4. Правила вычисления производной
- •9.5. Производные высших порядков
- •Глава 9
- •Глава 10. Приложения производной
- •10.1. Свойства дифференцируемых функций
- •10.2. Правило Лопиталя
- •10.3. Возрастание и убывание функций. Экстремумы функции
- •10.4. Наибольшее и наименьшее значения функции на отрезке
- •10.5. Выпуклость и вогнутость функции. Точки перегиба
- •10.6. Асимптоты графика функции
- •10.7. Общая схема исследования функций и построение их графиков
- •Глава 10
- •Глава 11. Дифференциал функции
- •11.1. Понятие дифференциала функции
- •11.2. Применение дифференциала в приближенных вычислениях
- •Глава 11
10.4. Наибольшее и наименьшее значения функции на отрезке
При решении прикладных задач важное значение имеют задачи на нахождение наибольшего и наименьшего значений ( глобального максимума и глобального минимума) функции на каком-либо промежутке.
Согласно теореме
Вейерштрасса (§ 8.4), если функция
![]() непрерывна
на отрезке
непрерывна
на отрезке
![]() ,
то она принимает на нем наибольшее и
наименьшее значения. Они могут достигаться
как в точках экстремума, так и на концах
отрезка. Например, на рис. 10.9
ВСТАВИТЬ наибольшее значение функция
имеет на конце отрезка, в точке
,
то она принимает на нем наибольшее и
наименьшее значения. Они могут достигаться
как в точках экстремума, так и на концах
отрезка. Например, на рис. 10.9
ВСТАВИТЬ наибольшее значение функция
имеет на конце отрезка, в точке
![]() ,
а наименьшее – в точке минимума
,
а наименьшее – в точке минимума
![]() .
.
Для отыскания наибольшего и наименьшего значений на отрезке следует выполнить следующие действия:
1) найти производную
![]() ;
;
2) найти критические
точки функции, в которых
![]() или не существует;
или не существует;
3) найти значения
функции в критических точках и на концах
отрезка и выбрать из них наибольшее
![]() и наименьшее
и наименьшее
![]() .
.
Пример
10.11. Найти наибольшее и наименьшее
значения функции
![]() на отрезке
на отрезке
![]() .
Вычисляем производную
.
Вычисляем производную
![]() .
Точек, в которых производная не существует,
у данной функции нет. Находим точки, в
которых производная равна нулю, получаем
.
Точек, в которых производная не существует,
у данной функции нет. Находим точки, в
которых производная равна нулю, получаем
![]() .
Вычисляем значения функции в этой точке
и на концах отрезка:
.
Вычисляем значения функции в этой точке
и на концах отрезка:
![]() ;
;
![]() ;
;
![]() .
Следовательно,
.
Следовательно,
![]() ,
,
![]() .
.
Замечание: На
интервале
![]() функция
достигает наибольшего или наименьшего
значения только в точках локальных
экстремумов.
функция
достигает наибольшего или наименьшего
значения только в точках локальных
экстремумов.
10.5. Выпуклость и вогнутость функции. Точки перегиба
Рассмотрим
дифференцируемую функцию
![]() .Функция
.Функция
![]() называется выпуклой на интервале
называется выпуклой на интервале
![]() ,
если все точки графика расположены ниже
любой касательной, проведенной к графику
функции, и вогнутой, если точки
графика расположены выше касательной.
,
если все точки графика расположены ниже
любой касательной, проведенной к графику
функции, и вогнутой, если точки
графика расположены выше касательной.

Обратимся к рис.
10.10. На интервале
![]() функция выпуклая, на интервале
функция выпуклая, на интервале
![]() – вогнутая.
– вогнутая.
Точка, в которой
меняется направление выпуклости функции,
называется точкой перегиба. На рис.
10.10 точкой перегиба является точка
![]() .
.
Для дважды дифференцируемых функций выполняются следующие теоремы.
Теорема
1. Если вторая производная
![]() функции
функции
![]() положительна (отрицательна) на интервале
положительна (отрицательна) на интервале
![]() ,
то функция является вогнутой (выпуклой)
на этом интервале.
,
то функция является вогнутой (выпуклой)
на этом интервале.
Теорема
2 (необходимое условие перегиба).
Если точка
![]() является точкой перегиба данной функции,
то вторая производная
является точкой перегиба данной функции,
то вторая производная
![]() обращается в точке
обращается в точке
![]() в нуль или не существует.
в нуль или не существует.
Теорема
3 (достаточное условие перегиба).
Если вторая производная
![]() дважды дифференцируемой функции
дважды дифференцируемой функции
![]() при переходе через некоторую точку
при переходе через некоторую точку
![]() меняет свой знак, то точка
меняет свой знак, то точка
![]() является точкой перегиба данной
функции.
является точкой перегиба данной
функции.
Из этих теорем
вытекает схема исследования на выпуклость
и вогнутость дважды дифференцируемой
функции
![]() :
:
-
находим вторую производную
 ;
; -
находим точки, в которых
 или
не существует;
или
не существует; -
найденные точки делят область определения второй производной на интервалы, в каждом из которых
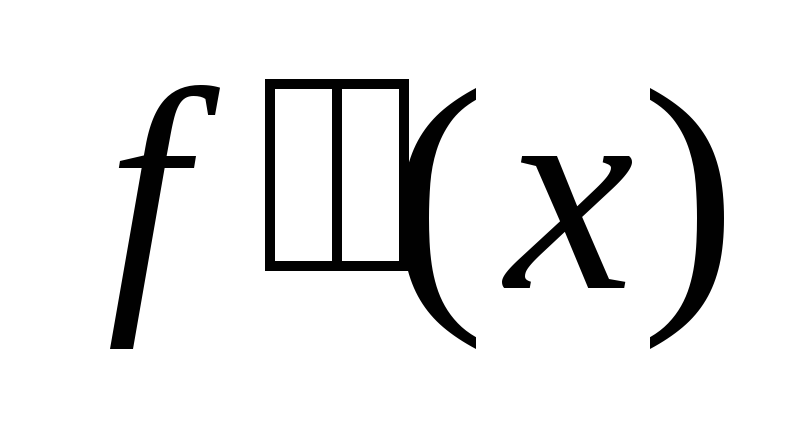 сохраняет свой знак. На интервалах, где
сохраняет свой знак. На интервалах, где
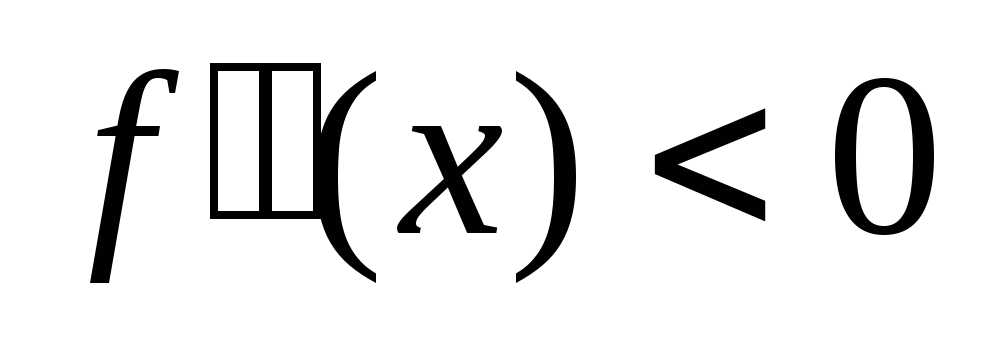 ,
функция является выпуклой, на интервалах,
где
,
функция является выпуклой, на интервалах,
где
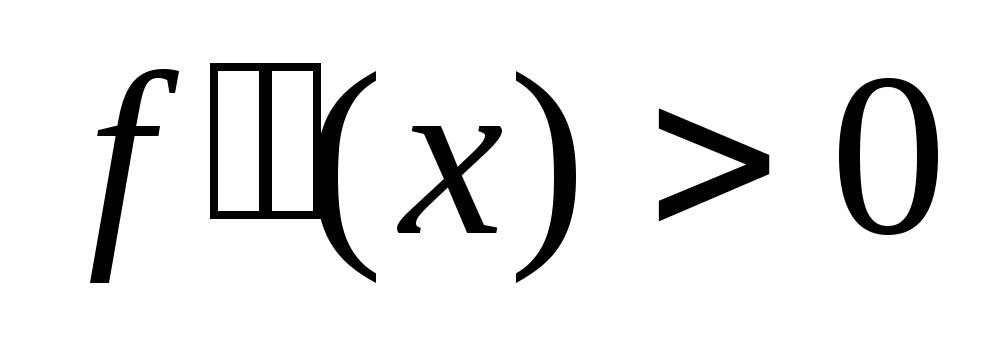 – вогнутой;
– вогнутой; -
находим значения функции в точках перегиба.
Пример
10.12. Функция
![]() выпукла на интервале
выпукла на интервале
![]() ,
вследствие того, что
,
вследствие того, что
![]() ,
и вогнута на интервале
,
и вогнута на интервале
![]() ,
т.к.
,
т.к.
![]() ;
следовательно, точка
;
следовательно, точка
![]() является точкой перегиба.
является точкой перегиба.
