
- •Раздел 5 основы дифференциального исчисления
- •Глава 9. Производная функции
- •9.1. Определение производной.
- •9.2. Связь между непрерывностью и существованием производной
- •9.3. Таблица производных
- •9.4. Правила вычисления производной
- •9.5. Производные высших порядков
- •Глава 9
- •Глава 10. Приложения производной
- •10.1. Свойства дифференцируемых функций
- •10.2. Правило Лопиталя
- •10.3. Возрастание и убывание функций. Экстремумы функции
- •10.4. Наибольшее и наименьшее значения функции на отрезке
- •10.5. Выпуклость и вогнутость функции. Точки перегиба
- •10.6. Асимптоты графика функции
- •10.7. Общая схема исследования функций и построение их графиков
- •Глава 10
- •Глава 11. Дифференциал функции
- •11.1. Понятие дифференциала функции
- •11.2. Применение дифференциала в приближенных вычислениях
- •Глава 11
10.3. Возрастание и убывание функций. Экстремумы функции
Напомним, что
функция называется возрастающей
(убывающей) на интервале
![]() ,
если для любых
,
если для любых
![]() и
и
![]() из этого интервала, удовлетворяющих
неравенству
из этого интервала, удовлетворяющих
неравенству
![]() выполняется неравенство
выполняется неравенство
![]()
![]() .
.
Теорема.
Если функция
![]() ,
дифференцируемая на интервале
,
дифференцируемая на интервале
![]() ,
не убывает (не возрастает) на этом
интервале, то ее производная
неотрицательна (неположительна), т. е.
,
не убывает (не возрастает) на этом
интервале, то ее производная
неотрицательна (неположительна), т. е.
![]()
![]()
Доказательство.
Пусть х – произвольное значение из
интервала
![]() .
Придадим этому значению х приращение
.
Придадим этому значению х приращение
![]() ,
такое, чтобы точка
,
такое, чтобы точка
![]() принадлежала интервалу
принадлежала интервалу
![]() .
Если
.
Если
![]() –
неубывающая функция, то
–
неубывающая функция, то
![]() при
при
![]() и
и
![]() при
при
![]() .
В обоих случаях
.
В обоих случаях
![]() и, следовательно,
и, следовательно,
![]() .
.
Если
![]() –невозрастающая
функция, то
–невозрастающая
функция, то
![]() и
и
![]() .
.
Теорема.
Если функция
![]() ,
дифференцируемая на интервале
,
дифференцируемая на интервале
![]() ,
удовлетворяет условию
,
удовлетворяет условию
![]()
![]() ,
то эта функция возрастает (убывает) на
этом интервале.
,
то эта функция возрастает (убывает) на
этом интервале.
Доказательство. Согласно теореме Лагранжа,
![]() ,
,
где
![]() ,
,
![]() ,
,
![]() .
Следовательно, если
.
Следовательно, если
![]() ,
и
,
и
![]() ,
то
,
то
![]() ,
т.е.
,
т.е.
![]() и данная функция возрастает для всех
и данная функция возрастает для всех
![]() .
.
Если
![]() и
и
![]() ,
то
,
то
![]() ,
т.е.
,
т.е.
![]() ,
и данная функция убывает для всех
,
и данная функция убывает для всех
![]() .
.
Пример
10.6. Найдем интервалы возрастания и
убывания функции
![]() .
Производная функции
.
Производная функции
![]() на интервале
на интервале
![]() .
Следовательно, функция убывает для всех
.
Следовательно, функция убывает для всех
![]() .
Производная
.
Производная
![]() на интервале
на интервале
![]() ,
следовательно, функция возрастает для
всех
,
следовательно, функция возрастает для
всех
![]() .
.

Функция имеет в
точке
![]() (рис. 10.4) локальный
максимум (минимум), если существует
такая окрестность точки
(рис. 10.4) локальный
максимум (минимум), если существует
такая окрестность точки
![]() ,
что для всех x из этой
окрестности выполняется неравенство
,
что для всех x из этой
окрестности выполняется неравенство
![]()
![]() .
.
Максимум или минимум функции называется экстремумом функции. По определению, экстремумы могут достигаться лишь внутри области определения.
Теорема
(необходимое условие существования
экстремума). Если функция
![]() ,
дифференцируемая в интервале
,
дифференцируемая в интервале
![]() ,
имеет в точке
,
имеет в точке
![]() ,
экстремум, то ее производная в этой
точке, если она существует, равна нулю.
,
экстремум, то ее производная в этой
точке, если она существует, равна нулю.
|
|
(10.2) |
Эта теорема является следствием теоремы Ферма.
Точки, в которых выполняется необходимое условие экстремума (производная равна нулю или не существует), называются стационарными (или критическими).
Таким образом, если в какой либо точке имеется экстремум, то эта точка критическая. Обратное утверждение неверно. Критическая точка не обязательно является точкой экстремума.
Пример
10.7. Функция
![]() не имеет экстремума в точке
не имеет экстремума в точке
![]() ,
хотя ее производная
,
хотя ее производная
![]() обращается в этой точке в нуль (рис.
10.5).
обращается в этой точке в нуль (рис.
10.5).
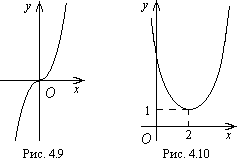
Теорема
(достаточное условие существования
экстремума). Если при переходе через
критическую точку
![]() производная дифференцируемой функции
меняет знак с плюса (минуса) на минус
(плюс), то в точке
производная дифференцируемой функции
меняет знак с плюса (минуса) на минус
(плюс), то в точке
![]() функция имеет максимум (минимум). Если
же при переходе через точку
функция имеет максимум (минимум). Если
же при переходе через точку
![]() производная знака не меняет, то в этой
точке функция
производная знака не меняет, то в этой
точке функция
![]() экстремума не имеет.
экстремума не имеет.
Доказательство.
Допустим, что
![]() меняет знак с плюса на минус. Тогда в
достаточно малой окрестности точки
меняет знак с плюса на минус. Тогда в
достаточно малой окрестности точки
![]() слева от
слева от
![]() функция
функция
![]() возрастает и
возрастает и
![]() ,
а справа от нее функция
,
а справа от нее функция
![]() убывает и
убывает и
![]() .
Следовательно, для всех х из достаточно
малой окрестности точки
.
Следовательно, для всех х из достаточно
малой окрестности точки
![]() (кроме самой этой точки) выполняется
неравенство
(кроме самой этой точки) выполняется
неравенство
![]() ,
т. е. в точке
,
т. е. в точке
![]() функция
функция
![]() имеет максимум.
имеет максимум.
Доказательство в случае обратной смены знака аналогичное.
Предположим, что
при переходе через точку
![]() производная функции не меняет знак.
Тогда как слева, так и справа от
производная функции не меняет знак.
Тогда как слева, так и справа от
![]() функция либо возрастает, либо убывает,
следовательно, не имеет экстремума.
функция либо возрастает, либо убывает,
следовательно, не имеет экстремума.
При исследовании функции на экстремум с помощью первой производной
-
находим производную функции
 ;
;
-
находим критические точки функции, т.е. корни уравнения
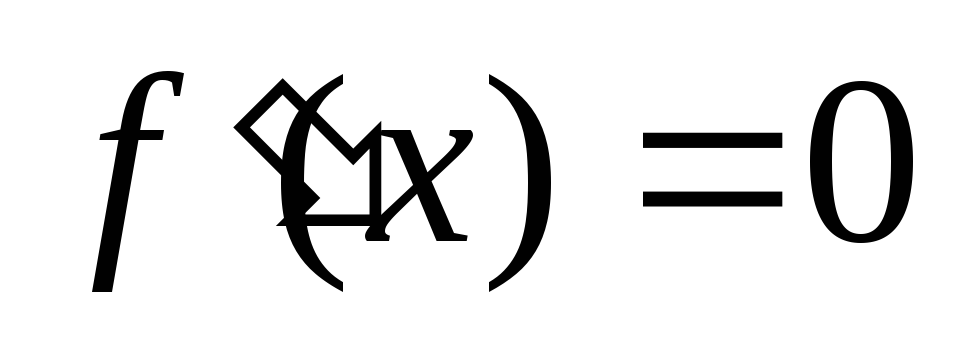 ,
или точки, в которых производная не
существует;
,
или точки, в которых производная не
существует; -
вычисляем знак
 слева и справа от каждой критической
точки и делаем вывод о наличии экстремумов
функции;
слева и справа от каждой критической
точки и делаем вывод о наличии экстремумов
функции; -
вычисляем значения функции в точках экстремума.
Пример
10.8. Найдем экстремумы функции
![]() .
Находим производную
.
Находим производную
![]() .
Точек, в которых производная не существует,
у данной функции нет –
.
Точек, в которых производная не существует,
у данной функции нет –
![]() определена на всей числовой оси.
Приравнивая ее к нулю, получаем
определена на всей числовой оси.
Приравнивая ее к нулю, получаем
![]() ,
или
,
или
![]() .
Если
.
Если
![]() ,
то
,
то
![]() ,
если
,
если
![]() ,
то
,
то
![]() .
Следовательно, точка
.
Следовательно, точка
![]() является точкой максимума функции.
Вычисляем соответствующее значение
функции
является точкой максимума функции.
Вычисляем соответствующее значение
функции
![]() (рис. 10.6).НАДО
ИЗМЕНИТЬ 4.10
(рис. 10.6).НАДО
ИЗМЕНИТЬ 4.10
Пример
10.9. Найдем экстремумы функции
![]() .
Область определения функции – вся
числовая ось. Находим производную
.
Область определения функции – вся
числовая ось. Находим производную
![]() .
Точек, в которых производная равна нулю,
нет. Производная функции не существует
в точке
.
Точек, в которых производная равна нулю,
нет. Производная функции не существует
в точке
![]() .
Если
.
Если
![]() ,
то
,
то
![]() ,
если
,
если
![]() ,
то
,
то
![]() .
Следовательно, точка
.
Следовательно, точка
![]() является точкой минимума функции.
Вычисляем соответствующее значение
функции
является точкой минимума функции.
Вычисляем соответствующее значение
функции
![]() (рис. 10.7).ВСТАВИТЬ
(рис. 10.7).ВСТАВИТЬ
Теорема
(второе достаточное условие существования
экстремума). Пусть функция
![]() имеет в точке
имеет в точке
![]() и ее окрестности непрерывные первую и
вторую производные, причем
и ее окрестности непрерывные первую и
вторую производные, причем
![]() ,
,
![]() .
Тогда функция
.
Тогда функция
![]() имеет в точке
имеет в точке
![]() минимум (максимум), если
минимум (максимум), если
![]() (
(![]() ).
).
Пример
10.10. Найдем экстремумы функции
![]() .
Вычисляем производные
.
Вычисляем производные
![]() ,
,
![]() .
Приравнивая первую производную к нулю,
получаем
.
Приравнивая первую производную к нулю,
получаем
![]() ,
,
![]() .
В точке
.
В точке
![]() функция имеет максимум, т.к.
функция имеет максимум, т.к.
![]() ,
а в точке
,
а в точке
![]() минимум, т.к.
минимум, т.к.
![]() .
.
(рис. 10.8).-ВСТАВИТЬ
