
- •Раздел 5 основы дифференциального исчисления
- •Глава 9. Производная функции
- •9.1. Определение производной.
- •9.2. Связь между непрерывностью и существованием производной
- •9.3. Таблица производных
- •9.4. Правила вычисления производной
- •9.5. Производные высших порядков
- •Глава 9
- •Глава 10. Приложения производной
- •10.1. Свойства дифференцируемых функций
- •10.2. Правило Лопиталя
- •10.3. Возрастание и убывание функций. Экстремумы функции
- •10.4. Наибольшее и наименьшее значения функции на отрезке
- •10.5. Выпуклость и вогнутость функции. Точки перегиба
- •10.6. Асимптоты графика функции
- •10.7. Общая схема исследования функций и построение их графиков
- •Глава 10
- •Глава 11. Дифференциал функции
- •11.1. Понятие дифференциала функции
- •11.2. Применение дифференциала в приближенных вычислениях
- •Глава 11
-
Раздел 5 основы дифференциального исчисления
Глава 9. Производная функции
9.1. Определение производной.
Производной функции в данной точке называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
|
|
(9.1) |
Наряду с обозначением
![]() для производной употребляются также
обозначения:
для производной употребляются также
обозначения:
![]() ,
,
![]() ,
,
![]() .
.
Пример
9.1. Рассмотрим функцию
![]() с областью определения
с областью определения
![]() и произвольное значение аргумента х.
Пусть х получает приращение
и произвольное значение аргумента х.
Пусть х получает приращение
![]() .
В точке х функция принимает значение
.
В точке х функция принимает значение
![]() ,
в точке
,
в точке
![]() значение
значение
![]() .
Приращение функции
.
Приращение функции
![]() имеет вид
имеет вид
![]() .
.
Тогда отношение приращения функции к приращению аргумента равно
![]() .
.
По определению
![]() .
.
Производная
является функцией от х. В каждой
конкретной точке х производная
– это число. Например, если
![]() ,
то
,
то
![]() .
.
Процесс нахождения производной от данной функции называется ее дифференцированием.
Пусть S(t) – путь, пройденный телом к моменту времени t. Скорость тела в точке t равна
![]() ,
,
т.е.
производной
![]() от пройденного пути по времени.
от пройденного пути по времени.
Если Q – количество вещества, участвующего в данной химической реакции к моменту времени t, то
![]()
является скоростью изменения количества вещества.
Рассуждая подобным образом, приходим к выводу, что для любой функции y(x) ее производная равна скорости изменения этой функции. В этом заключается механический смысл производной.
Касательной
k к кривой в точке М
(рис. 9.1) называется
предельное положение секущей
![]() ,
когда точка
,
когда точка
![]() по кривой стремится к точке М.
по кривой стремится к точке М.
x+Δx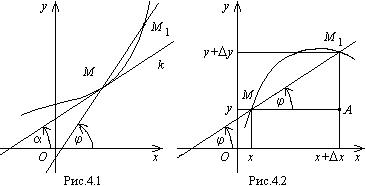
Рассмотрим
функцию
![]() в некоторой точке х (рис. 9.2). Перейдем
от точки х к новой точке
в некоторой точке х (рис. 9.2). Перейдем
от точки х к новой точке
![]() ,
,
![]() равно приращению функции
равно приращению функции
![]() ,
,
![]() .
Из
.
Из
![]() получаем
получаем
![]() ,
,
т.е.
![]() –тангенс угла наклона секущей
–тангенс угла наклона секущей
![]() к оси Ох. Пусть
к оси Ох. Пусть
![]() .
Тогда точка
.
Тогда точка
![]() стремится к точке М и, следовательно,
стремится к точке М и, следовательно,
![]() стремится к
стремится к
![]() ,
где
,
где
![]() – угол наклона касательной к прямой в
точке М.
– угол наклона касательной к прямой в
точке М.
Так как
![]() ,
то при
,
то при
![]() ,
стремящемся к нулю, отношение
,
стремящемся к нулю, отношение
![]() стремится к
стремится к
![]() ,
или
,
или
![]() .
.
Таким
образом,
![]() .
.
Следовательно, значение производной функции в точке равно тангенсу угла наклона касательной, проведенной к графику функции в данной точке. В этом состоит геометрический смысл производной.
Знание геометрического
смысла производной позволяет построить
уравнение касательной к данной линии
в данной точке
![]()
![]() .
(9.2)
.
(9.2)
Нормалью
линии в данной точке
![]() называется перпендикуляр к касательной
в точке
называется перпендикуляр к касательной
в точке
![]() .
Уравнение нормали
.
Уравнение нормали
![]() .
(9.3)
.
(9.3)
Пример
9.2. Напишем уравнение касательной
![]() и нормали
и нормали
![]() к параболе
к параболе
![]() в точке
в точке
![]() .
(рис. 9.3). При
.
(рис. 9.3). При
![]() ,
,
![]() ,
т.е. касательную и нормаль проводим в
точке
,
т.е. касательную и нормаль проводим в
точке
![]() .
.
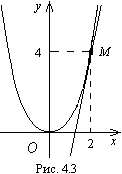
Вычисляем угловой
коэффициент касательной. Производная
функции
![]() равна
равна
![]() .
В точке
.
В точке
![]() имеем
имеем
![]() .
Следовательно,
.
Следовательно,
![]() .
Согласно формуле (9.2), уравнение касательной
принимает вид
.
Согласно формуле (9.2), уравнение касательной
принимает вид
![]() .
Преобразовывая, получаем
.
Преобразовывая, получаем
![]() .
Для того, чтобы написать уравнение
нормали, используем формулу (9.3). Уравнение
нормали имеет вид
.
Для того, чтобы написать уравнение
нормали, используем формулу (9.3). Уравнение
нормали имеет вид
![]() ,
преобразовывая, получаем
,
преобразовывая, получаем
![]() .
.
