Министерство образования и науки Украины

Национальный Технический Университет

"Харьковский Политехнический Институт"

Кафедра «Системный анализ и управление»

ОТЧЕТ

по лабораторной работе № 1

на тему:

«Исследование систем управления по отклонению»

Выполнили:

ст. гр. ИФ-55Б

Губенко С.А.

Калюх С.Н.

Сорокоумова М.А.

Проверил:

Дорофеев Ю.И.

Харьков - 2009

ВЫПОЛНЕНИЕ ЗАДАНИЯ:

1. Объект управления задан двумя передаточными функциями:

, ,

где u(t) – управляющее воздействие, f(t) – возмущающее воздействие.

Необходимо выбрать значения параметров передаточных функций, описывающих объект управления:

betta1 = 3, gamma1 = 2, Ku = 5, Kf = 7, alfa1 = 2, alfa2 = 1.

2. Решим задачу стабилизации, то есть найдем значения коэффициентов ПИ-регулятора , обеспечивающие заданное расположение полюсов замкнутой системы.

Передаточная функция системы имеет вид:

.

Воспользуемся критерием Рауса-Гурвица, и найдем значения коэффициентов ПИ-регулятора , обеспечивающие устойчивость заданной системы:

.

Характеристический полином полученной ПФ имеет вид:

.

Воспользуемся критерием Рауса-Гурвица:

,

,

Согласно критерию Рауса-Гурвица для полинома второй степени достаточно . Наши удовлетворяют этому условию и обеспечивают устойчивость заданной системы.

3. Реализовать модель исследуемой системы в среде SIMULINK в соответствии со структурной схемой:

, ,

(ПИ-регулятор).

Наша модель, построенная в SIMULINK:

4. Исследовать изменение ошибки системы при различных типах задающего воздействия в условиях отсутствия возмущающего воздействия:

1) , =1сек ()

Выводы: после того, как на 1-й секунде было подано задающее воздействие в виде единичного скачка, ПИ-регулятор позволил стабилизировать систему и вернуть её к первоначальному состоянию, то есть минимизировать ошибку на выходе.

2) , ()

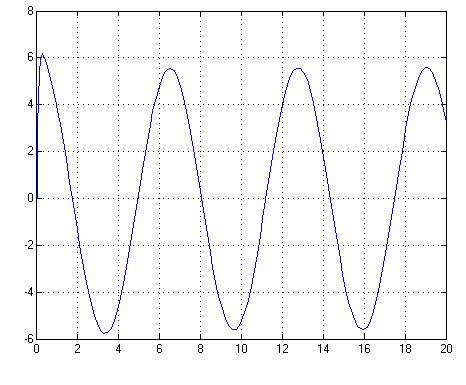
Выводы: на рисунке видно, что при задающем воздействии в виде синусоиды ПИ-регулятор стремится стабилизировать амплитуду ошибки на выходе системы.

5. Исследовать изменение ошибки системы при возникновении возмущающего воздействия:

1) , сек, сек;

Выводы: при подаче на 10-й секунде возмущающего воздействия ПИ-регулятор позволил свести ошибку регулирования к нулю.

2) , .

Выводы: как видно из графика, ПИ-регулятор не может погасить возмущение, возникающее при внешнем воздействии.