Исследование системы управления в Simulink

Путем получения копий элементов (Ctrl+ левая кнопка мыши) и их переноса составить схему для моделирования системы. Соединять элементы согласно схеме путем протаскивания левой кнопки мыши от выхода предыдущего элемента к входу последующего. При правильном соединении на схеме появляется черная линия (стрелка) связи. Появление красной штриховой линии означает, что связь не установлена. Необходимо начало или конец линии довести соответственно до выхода предыдущего или входа последующего элемента. Можно удалить красную линию и повторить построение линии связи.

Разветвление линии производится путем протаскивания мыши при нажатой кнопке Ctrl. Поворот линии производится путем отпускания и повторного нажатия левой кнопки мыши в месте поворота.

4. Ввести параметры элементов путем нажатия правой кнопки мыши и выбора строки параметров (parameters) конкретного элемента в диалоговом окне:

• коэффициенты числителя (Numerator) и знаменателя (Denominator) передаточной функции динамических элементов (в квадратных скобках через пробел).

• настроить блок подачи ступенчатого сигнала 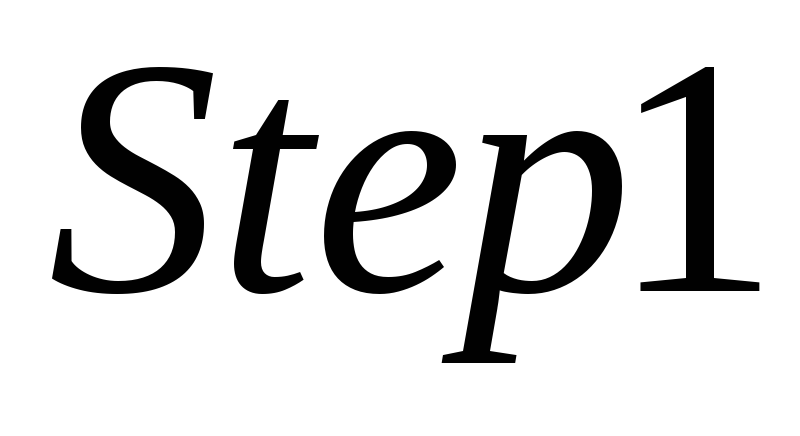для обеспечения ступенчатого изменения задающего воздействия от 0 до 1 при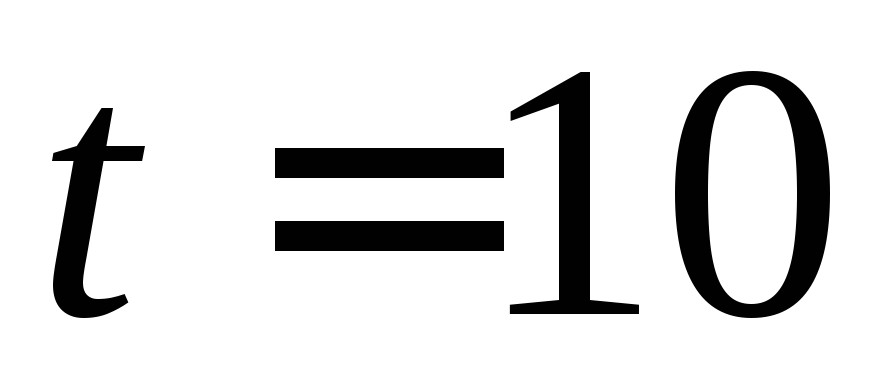шагов моделирования.

• установить 3 входа для осциллоскопа - двойной щелчок на осциллоскопе/ кнопка параметры/опция - количество осей 3. Вывести на осциллоскоп сигналы из трех точек схемы – задающее воздействие, возмущающее воздействие и выходной сигнал системы.

• Для PIDрегулятора ввести начальные значения коэффициентов пропорциональной составляющейKp=0.1, интегральной составляющейKi=0 и дифференциальной составляющейKd=0.

Моделирование работы системы при единичном ступенчатом задающем воздействии и анализ закономерностей работы системы при различных коэффициентах регулятора.

1. При введенных коэффициентах регулятора нажать кнопку «Startsimulation» для запуска процедуры моделирования работы системы. После окончания цикла моделирования сделать двойной щелок левой кнопки мыши на осциллоскопе. Для удобства просмотра графиков нажать кнопку автомасштабированияAutoscale(на кнопке изображен бинокль). В зависимость от математических моделей элементов системы и величины коэффициентаKpпереходной процесс может иметь различные значения. На рис. 6 приведен переходной процесс для случая, когда регулируемая переменная не выходит на заданное единичное значение (выходная величина вышла на уровень 0,7 вместо 1). Это означает, что коэффициентKpимеет малое значение. УвеличениеKp, как правило, приводит к увеличению степени колебательности системы (см. рис. 7) и переходу системы к неустойчивому состоянию (рис. 8).

2. Постепенно увеличивая коэффициент Kp, получить систему с повышенной степенью колебательности, путем дальнейшего увеличения коэффициента получить неустойчивую систему.

3. Уменьшая коэффициент Kp, получить переходной процесс с допустимой степенью колебательности – перерегулирование 20-30%, количество колебаний не более 2-х (см. рис. 9). При этом регулируемая переменная, как правило, не выходит на заданное значение 1.

4. Выход системы на заданное единичное значение обеспечивает интегральная составляющая регулятора. Вводим коэффициент интегральной части Ki=0,1 и проводим моделирование системы. Постепенно увеличивая коэффициентKiдобиваемся выхода системы после окончания переходного процесса на заданное значение1 (см. рис. 10).

Моделирование работы системы при ступенчатых задающем и возмущающем воздействиях. На блоке задать ступенчатое воздействие с 0 на 2 в момент времени 20 сек и провести моделирование работы системы. Переходной процесс отработки ступеньки по заданию и ступенчатого возмущающего воздействия приведен на рис. 11. График выходной переменной показывает, что система отрабатывает изменения задающего и возмущающего воздействий.

Моделирование работы системы при случайных возмущающих воздействиях. Отключить блоки и(или установить на них нулевые значения синалов). Подключить генератор случайного сигнала и формирующие фильтры. Провести моделирование работы системы. Убедиться, что при замкнутой системе влияние возмущающего воздействия уменьшается. На рис.12 амплитуда возмущающего воздействия составляетединиц, а амплитуда колебаний выходной переменной составляет примерно. Следовательно, система уменьшила влияние возмущающего воздействия примерно в 8 раз.

Подготовить отчет по проделанной работе, включающий схему моделирования, найденные значения коэффициентов регулятора, графики переходных процессов.

Отчитаться по проделанной работе.

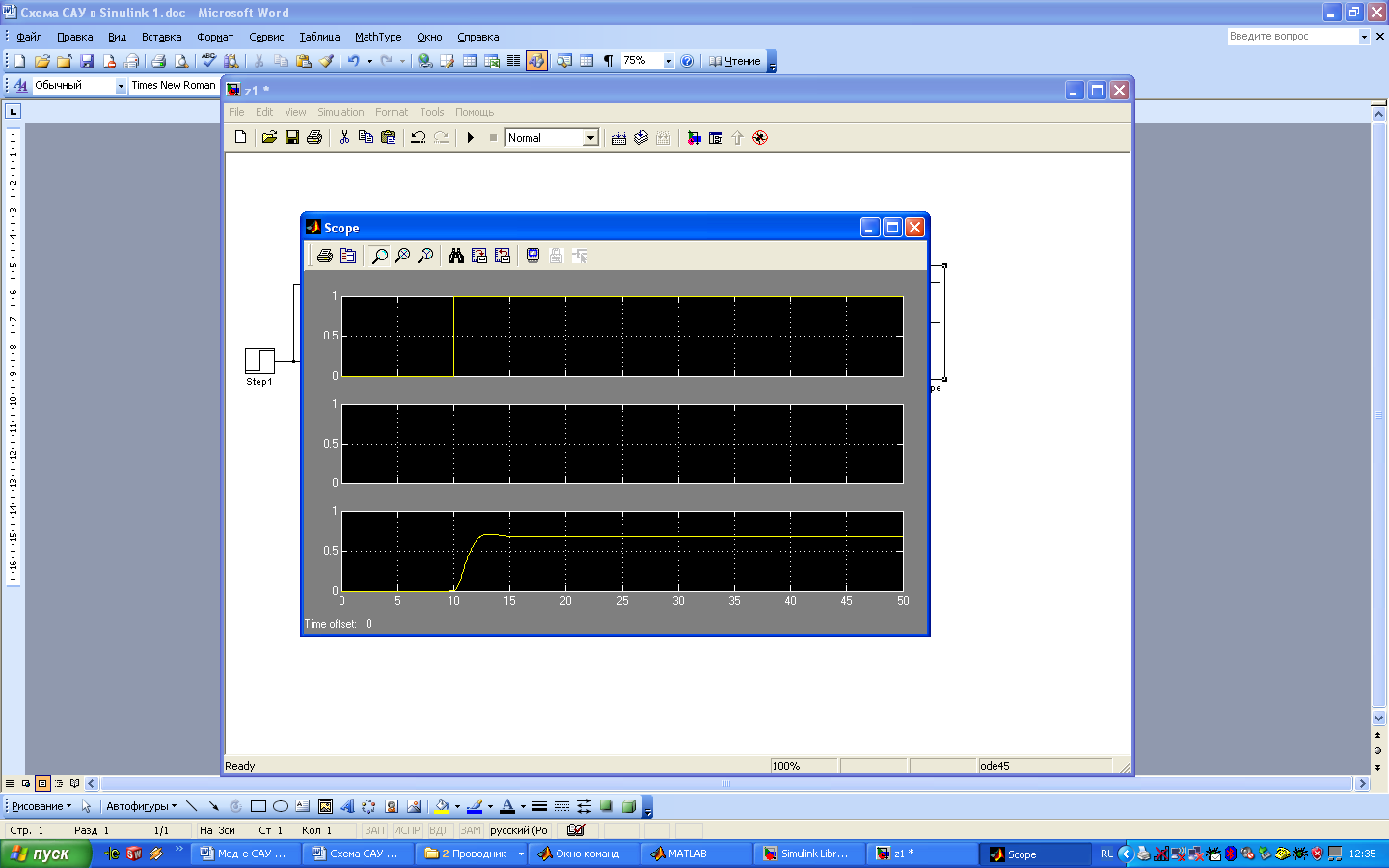
Рис. 6. Переходной процесс по задающему воздействию при малом коэффициенте пропорциональной составляющей регулятора

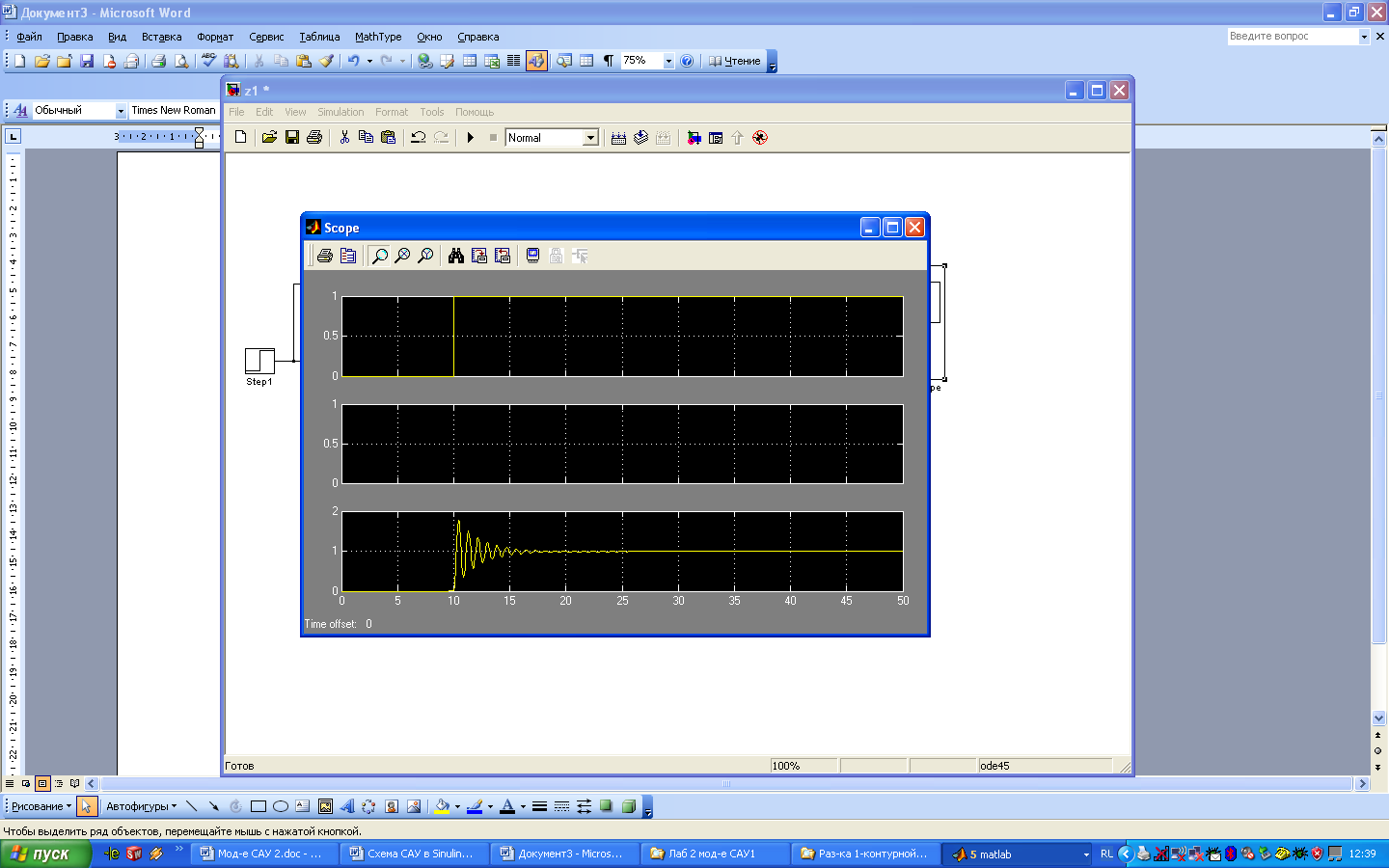
Рис. 7. Переходной процесс по задающему воздействию при большом коэффициенте пропорциональной составляющей регулятора

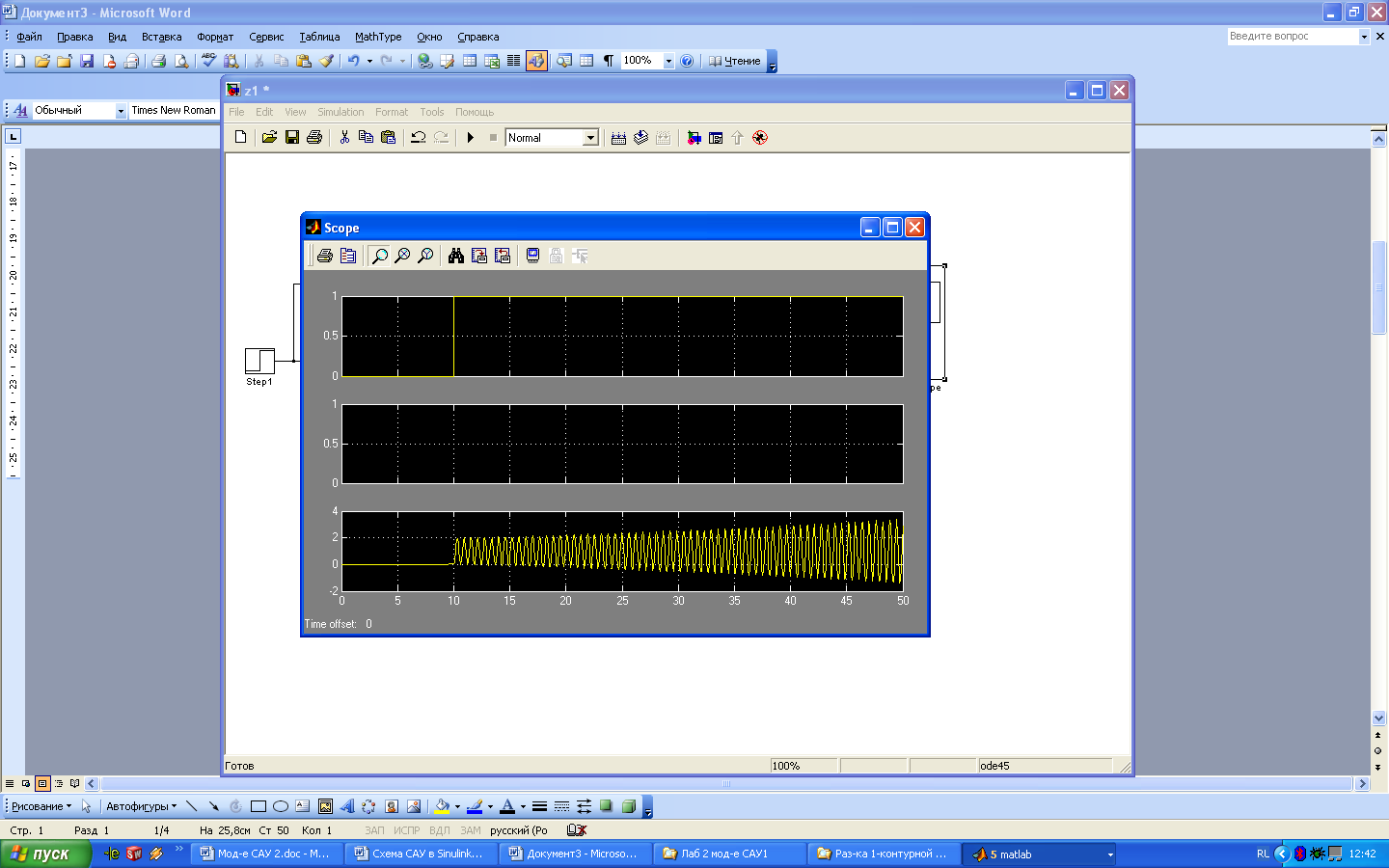
Рис. 8. Система управления неустойчивая

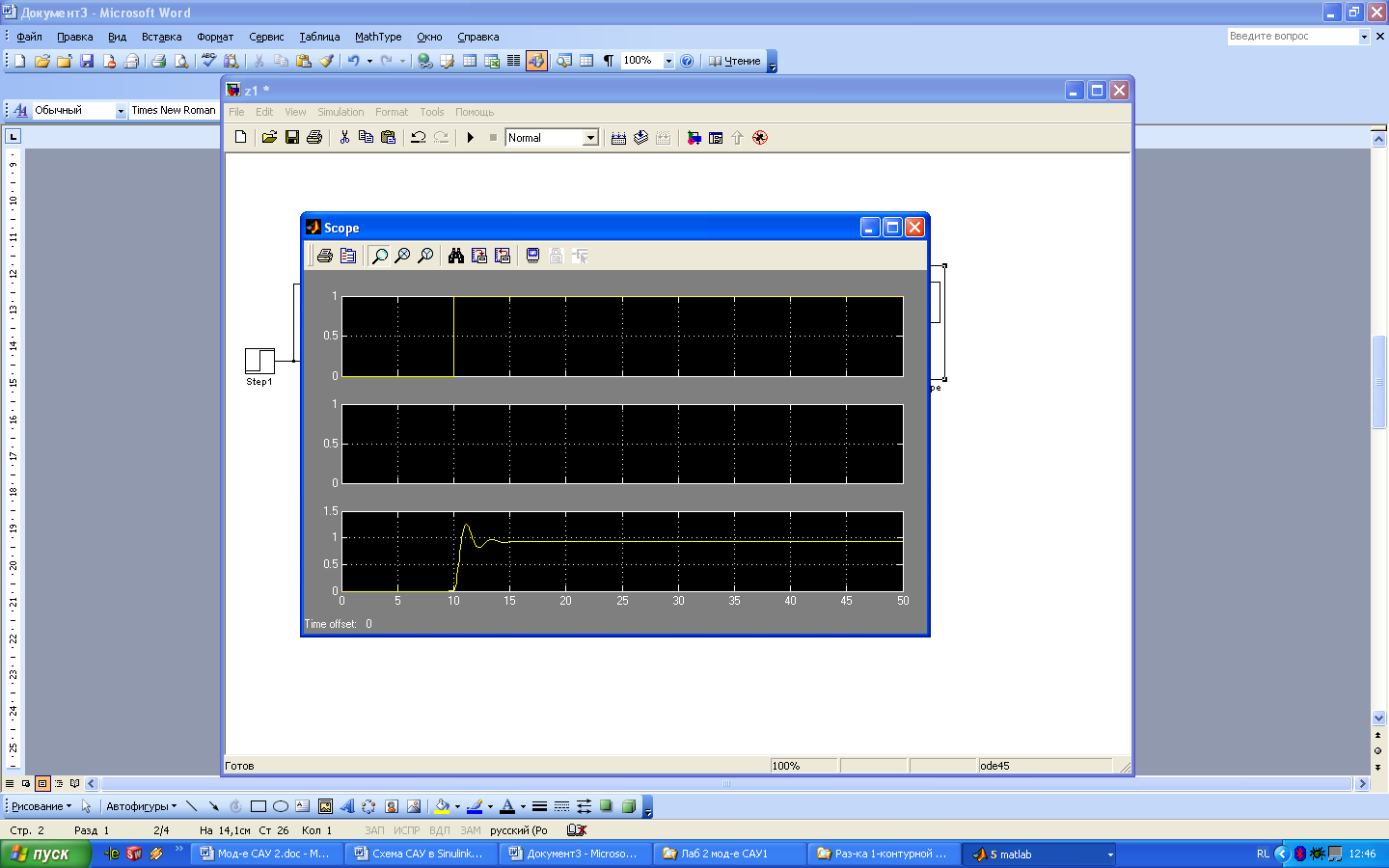
Рис. 9. Система управления имеет нормальный переходной процесс по степени колебательности, но не выходит на заданное значение

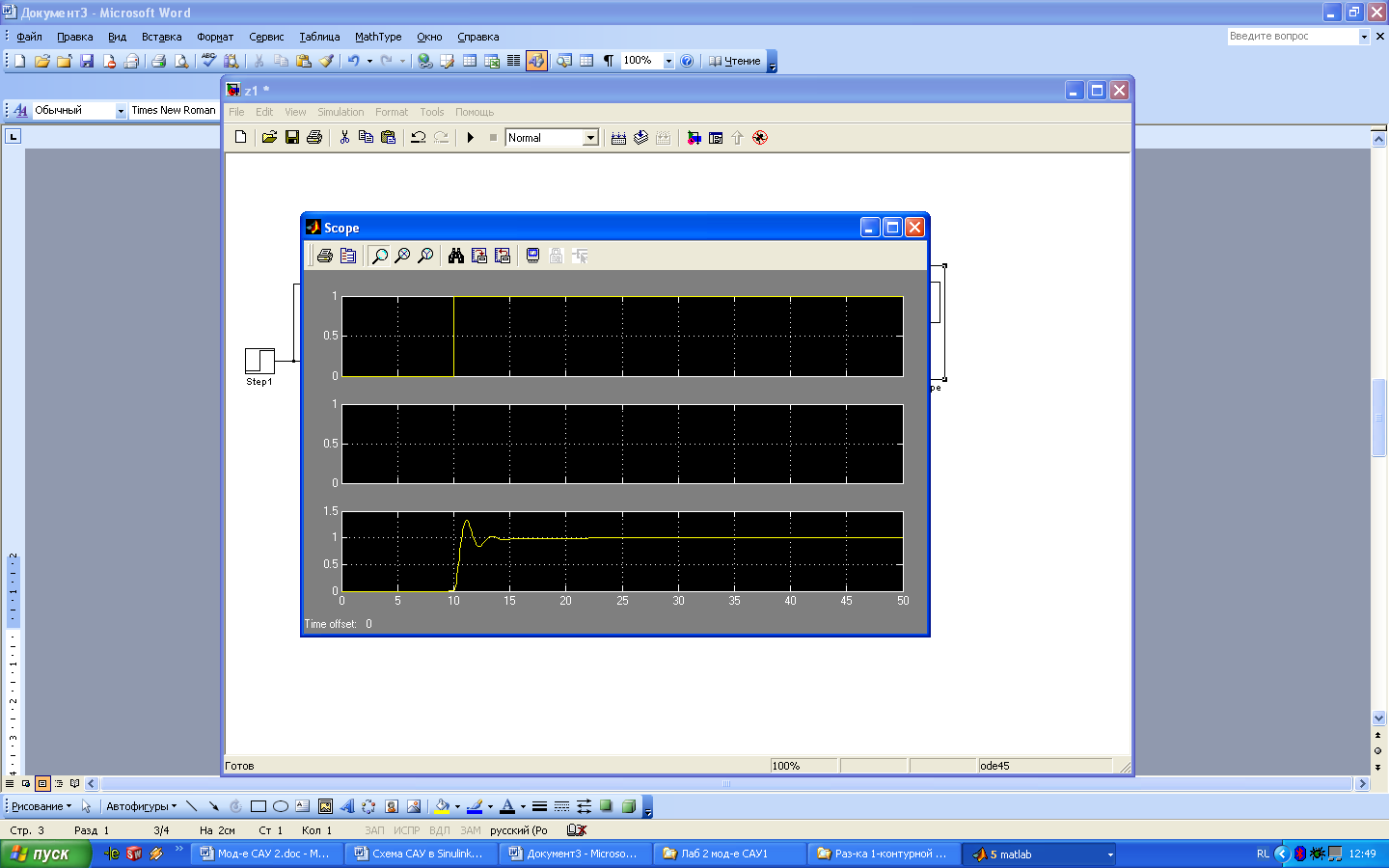
Рис. 10. Система управления имеет нормальный переходной процесс по степени колебательности и выходит на заданное значение

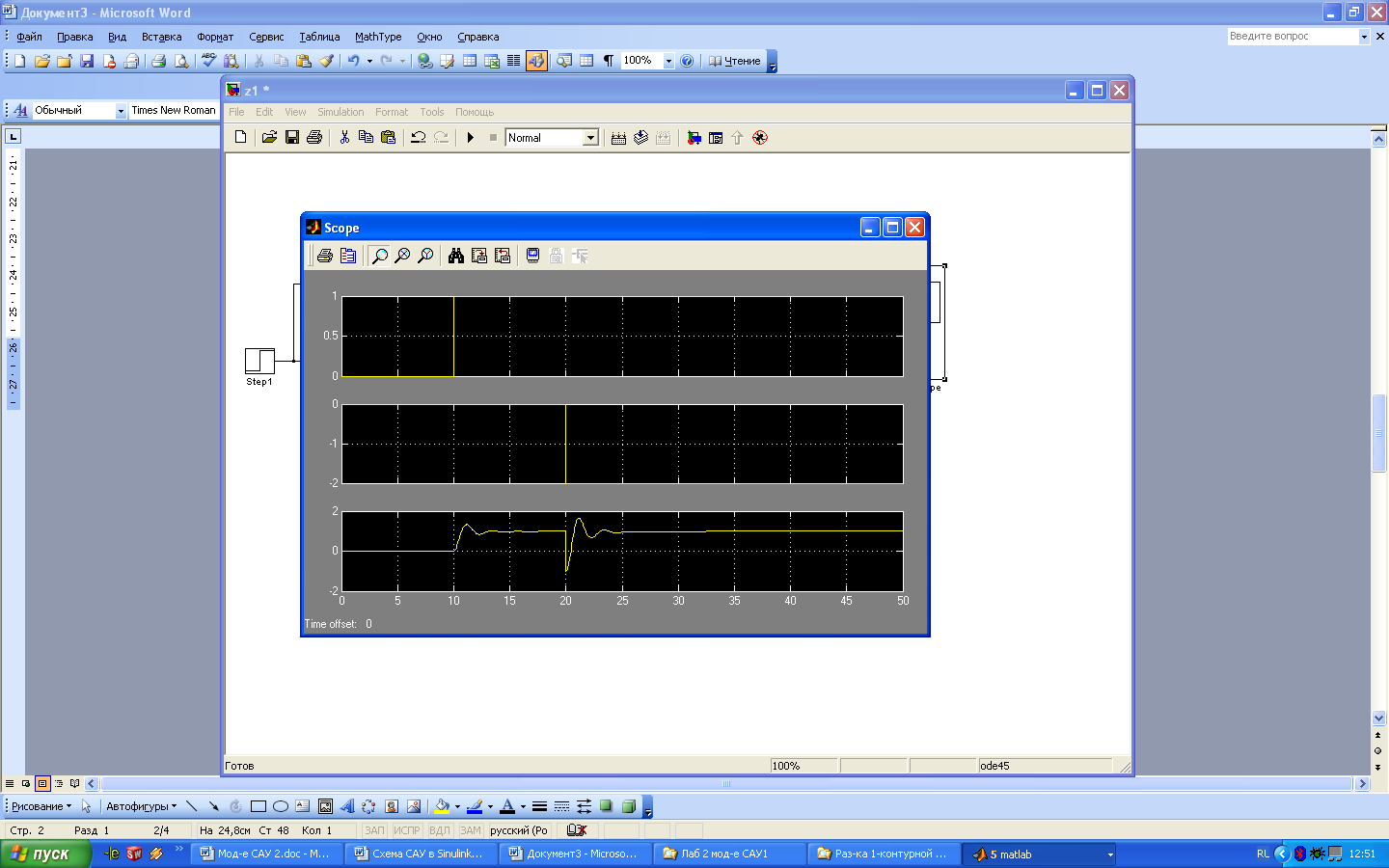
Рис. 11. Система управления отрабатывает задающее

и возмущающее воздействия

Рис. 12. Система управления отрабатывает стохастическое

возмущающее воздействие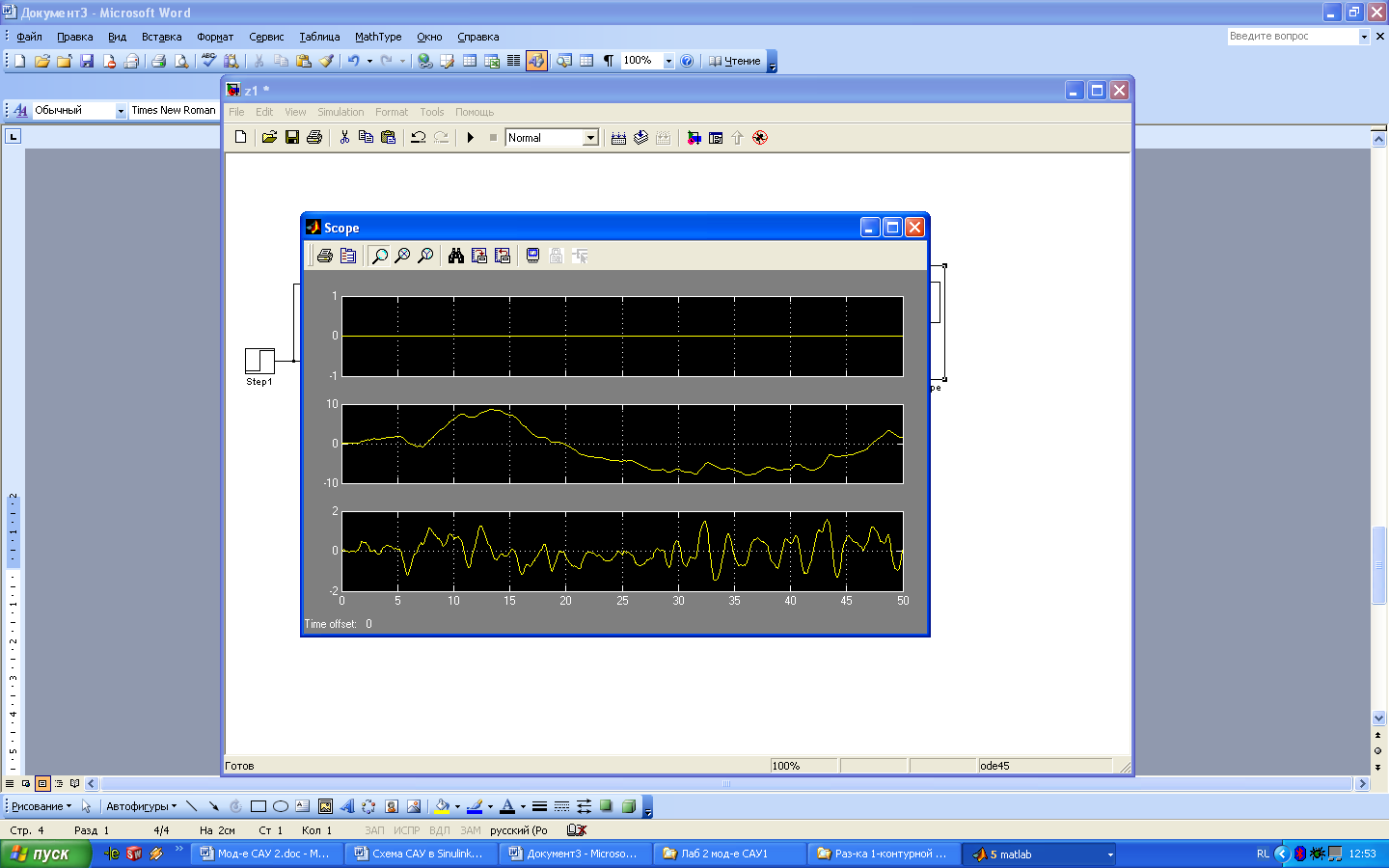

Список использованной литературы

1. Клюев А.С. Автоматическое регулирование. -М.: Энергия, 1973. – 392с.

2. Бесекерский В.А., Теория систем автоматического регулирования. -М.: Наука, 1972. –768с.

3. Цыпкин Я.З. Основы теории автоматических систем. -М.: Наука, 1977.- 560 с.

4. Зайцев Г.Ф. Теория автоматического управления и регулирования. -К.: Вища школа, 1975.- 424с.

5. Куропаткин П.В. Теория автоматического управления. -М.: Высшая школа, 1973.- 528с.

6. Первозванский А.А. Курс теории автоматического управления. -М.:Наука, 1986. –616с.

7. Юревич Е.И. Теория автоматического управления. -Л.: Энергия, 1975. – 416с.

8. Санковский Е.К. Вопросы теории автоматического управления. Статистический анализ и синтез САУ. -М.: Высшая школа, 1971. -232 с.

9. Дроздов Н.В. Системы автоматического управления с микроЭВМ. -Л.: Машиностроение, 1989. -284 с.

10. Филипс Ч., Харбор Р. Системы управления с обратной связью. -М.: ЛБЗ, 2001. –616с.

11. Дорф Р, Бишоп Р. Современные системы управления. -М.: ЛБЗ, 2002. – 832с.

12. Топчеев Ю.И., Ципляков А.П. Задачник по теории автоматического регулирования. -М.: Машиностроение, 1977. – 592с.

13. Потемкин В.Г. MATLAB 5 для студентов. -М.: ДиалогМифи, 1998. – 314с.

14. Потемкин В.Г. MATLAB: справочное пособие. -М.: ДиалогМифи, 1997. – 350с.

15. Медведев В.С., Потемкин В.Г. ControlSystemToolbox. -М.: Диалог-Мифи, 1999. – 278с.

16. Дьяконов В., Круглов В. MATLAB Анализ, идентификация и моделирование систем: специальный справочник. -М.: Питер, 2002. – 448с.

17. Дэбни Д., Харман Т. Simulink 4. Секреты мастерства. -М.: Бином, 2003. –403с.

18. Дьяконов В. Simulink4: специальный справочник. -М.: Питер, 2002. – 528с.

19. Черных И.В. Simulink. Среда создания инженерных приложений. -М.: ДиалогМифи, 2004. – 496с

20. Дьяконов В. MATLAB 6/6.1/6.5 Simulink 4/5 в математике и моделировании. -М.: Салон-пресс, 2003. – 576с.