Литература

1. Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления с примерами в системе MatLab. СПб.: Наука, 1999.

2. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. - М.: Наука, 1975.

3. Дьяконов В. MATLAB 6: Учебный курс. Питер. 2001.

4. Дьяконов В., Абраменкова И., Круглов В. MATLAB с пакетами расширений. Нолидж. 2001.

5. Сборник задач по теории автоматического регулирования и управления/ Под редакцией В. А. Бесекерского. - M.: Наука, 1978.

ВРЕМЯ, ОТВЕДЕННОЕ НА ВЫПОЛНЕНИЕ РАБОТЫ

Подготовка к работе – 2,0 акад.часа

Выполнение работы – 1,0 акад.часа

Оформление работы – 1,0 акад.часа

32

Министерство образования и науки Российской Федерации

Саратовский государственный технический университет

Балаковский институт техники, технологии и управления

Исследование сау на фазовой плоскости

Методические указания к лабораторной работе по курсу «Теория автоматического управления» для студентов специальности 210100

Одобрено

редакционно –издательским советом

Балаковского интститута техники,

технологии и управления

Балаково 2004

Цель работы: Изучение метода фазового пространства (плоскости) на примере исследования свободного движения системы, описываемой дифференциальным уравнением 2-го порядка. Знакомство с нелинейными САУ и методами их исследования с помощью фазовых траекторий и припасовывания.

ОСНОВНЫЕ СВЕДЕНИЯ

1. Линейные сау.

Пусть исследуемая система описывается дифференциальным уравнением

(1)

Это уравнение может быть преобразовано к системе n дифференциальных уравнений первого порядка

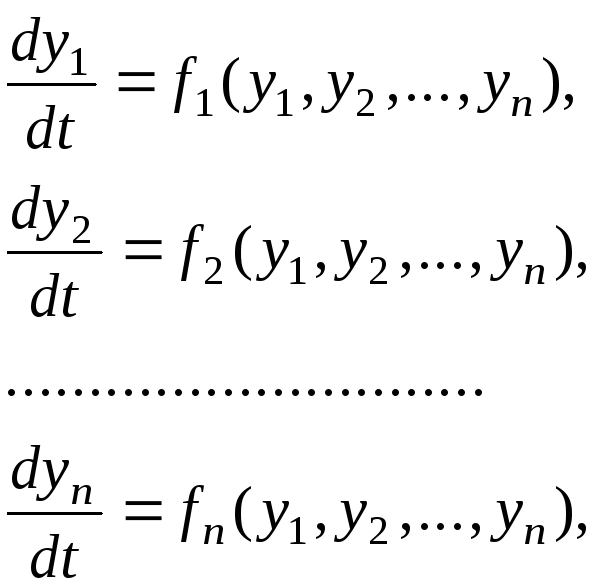(2)

С начальными условиями

(3)

2

1. Что такое предельный цикл, какие бывают предельные циклы и какие процессы имеют место в САУ при наличии предельного цикла?

2. Что собой представляет метод припасовывания?

3. Как в MATHCAD реализуется метод фазовых траекторий?

4. Как в MATHCAD реализуется метод припасовывания?

31

- выводы.

В выводах должна быть приведена оценка влияния корней характеристического уравнения САУ на вид фазовых траекторий. Необходимо также связать характер переходных процессов в исследуемой САУ с видом фазовых траекторий .

КОНТРОЛЬНЫЕ ВОПРОСЫ

5. Какое пространство называется фазовым ?

6. Как правильно выбрать фазовые переменные ?

7. Как построить фазовые траектории ?

8. Как определить направление движения изображающей точки ?

9. Каковы достоинства и недостатки метода фазовой плоскости ?

10. Что такое фазовый портрет ?

11. В чем заключается метод фазовых траекторий?

12. Какие переменные соответствуют осям, образующим фазовую плоскость?

13. Какие нелинейные статические характеристики Вы знаете?

14. Как получить уравнение фазовых траекторий?

15. Что такое особые линии нелинейных систем и какие особые линии Вы знаете?

30

Пусть, например, n=3 , т.е. рассматривается система 3-го порядка. Свяжем с каждой переменной свою ось координат в 3-х мерном пространстве. Такое пространство будем называть фазовым пространством.

Начиная с начального момента времени t=0 с течением времени координаты непрерывно меняются в соответствии с (2). В результате в фазовом пространстве будет иметь место некоторая траектория, которая образуется движением по ней точки М(t). Точка М называется изображающей точкой, а траектория по которой она движется – фазовая траектория.

Необходимо отметить, что производные по времени от координат изображающей точки М представляют собой проекции ее скорости V на оси координат, следовательно дифференциальные уравнения (2) являются уравнениями этих проекций. Таким образом, по значениям правых частей уравнений (2) можно судить в каждый момент времени о направлении движения изображающей точки М.

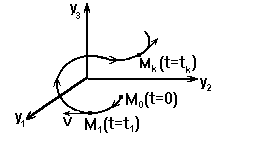
Рисунок 1- Фазовая траектория точки М в трехмерном пространстве

3

Если будет рассматриваться в уравнениях (2) две переменные и, то изображающая точка М будет двигаться не в пространстве, а на фазовой плоскости.

Совокупность фазовых траекторий называется фазовым портретом. Фазовый портрет дает наглядное представление о характере поведения исследуемой системы, однако, следует отметить, что при этом из рассмотрения исключено время. То есть мы не можем исследовать динамику системы. Для исследования динамических свойств необходимо решить дифференциальные уравнения (1) или (2).

Проведем исследование линейной системы 2-го порядка на фазовой плоскости. Запишем уравнение, описывающее поведение системы

(4)

Введем переменную

(5)

и приведем уравнение (4) к виду

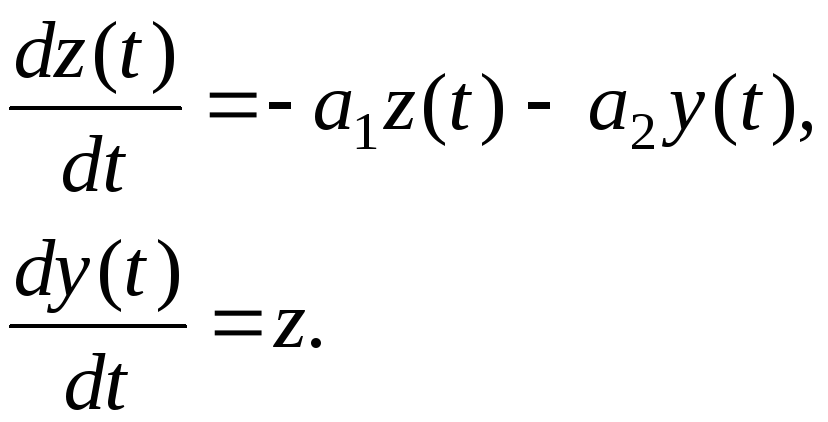(6)

Разделив первое уравнение системы (6) на второе, исключим время

(7)

4

2.2. Построить фазовые траектории для различных начальных состояний САУ так , чтобы получить полный фазовый портрет, характеризующий поведение нелинейной системы.

2.3. Построить переходные процессы для выходной координаты y(t).

2.4. При наличии предельного цикла определить его параметры: амплитуду и частоту.

2.5. Исследовать влияние параметров САУ k, T и b на параметры предельного цикла.

СОДРЕЖАНИЕ ОТЧЕТА

Отчет должен содержать:

- задание на лабораторную работу, ее цель и задачи;

- исходное уравнение исследуемой линейной системы и уравнение фазовых траекторий;

- программу в MATHCAD получения фазовых траекторий;

- фазовые портреты исследуемой линейной системы;

- структурную схему системы, передаточные функции ее элементов, характеристику нелинейного элемента;

- дифференциальные уравнения, описывающие поведение нелинейной системы;

- программу моделирования в MATHCAD 7;

-

29

полученные фазовые портреты, переходные процессы, параметры автоколебаний и результаты исследования влияния параметров САУ на параметры автоколебаний;

Таблица 2

№	b	c	k	T
1	2	0,5	1	1
2	1	0,5	1	1
3	1	0,2	1	0,5
4	1	1	2	0,5
5	0,5	0,3	1,5	0,4
6	1	1	2	2
7	0,5	0,4	1	1,5
8	1	0,5	1	3
9	1,5	0,3	2	5
10	0,8	0,5	1	0,8
11	0,9	0,5	3	0,2
12	1,5	2	1,5	0,7
13	2	0,5	2	1
14	1	0,5	2	1,5
15	1	0,2	3	1
16	1	1	4	0,5
17	0,5	0,3	2	0,7
18	1	1	1	0,3
19	0,5	0,4	2	0,05
20	1	0,5	2	1
21	1,5	0,3	3	2
22	0,8	0,5	1	0,09
23	0,9	0,5	1	0,1
24	1,5	2	1	0,6

28

Решение этого дифференциального уравнения определяет совокупность интегральных кривых на фазовой плоскости , причем каждая кривая соответствует вполне определенному значению постоянной времени.

В установившемся состоянии, согласно (7)

Так как правая часть этого уравнения неопределенна, то направление касательных в точке y=z=0 также является неопределенным. Для уравнения (7) существует 6 таких точек , называемых особыми. Рассмотрим их. 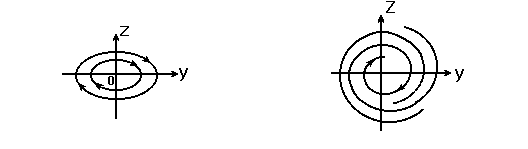Рисунок 2 - Особая точка “центр” Рисунок 3 - Особая точка

“Устойчивый фокус”

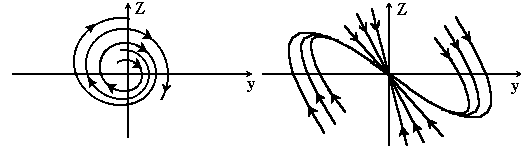
Рисунок 4 - Особая точка Рисунок 5 - Особая точка

“

5

Неустойчивый фокус” “Устойчивый узел”

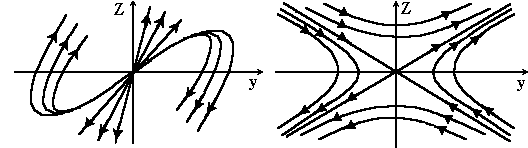
Рисунок 6 - Особая точка Рисунок 7 - “Седло”

“Неустойчивый узел”