- •РАсчет Замкнутой системы iiIпорядка
- •Структурная схема
- •1.Составить математическую модель сау
- •2.Получить дифференциальное уравнение относительно выхода по задающему и возмущающему воздействиям
- •3.Определить передаточную функцию системы.
- •3.3. Передаточную функцию замкнутой системы по ошибке при действии задающего воздействия и равенстве 0 возмущающего воздействия
- •3.4. Передаточную функцию замкнутой системы по ошибке при действии возмущающего воздействия и равенстве 0 задающего воздействия
- •4.Вычислить временные характеристики
- •4.2.С помощью обратного преобразования Лапласа найти переходную и весовую функции
- •5.Частотные характеристики
- •5.1.Афчх
- •5.4.Логорифмитическая амплитудно-частотная характеристика
- •6.Произвести анализ устойчивости сау:
- •6.1.Критерий Вышнеградского
- •6.2.Критерий Рауса-Гурвица
- •6.3.Критерий Михайлова
- •6.4.Критерий Найквиста
- •Определение устойчивости по лачх
3.3. Передаточную функцию замкнутой системы по ошибке при действии задающего воздействия и равенстве 0 возмущающего воздействия
W1*W2*W3*W4*W6*W7





G(s) E(s) Y(s)

Y(s)
Схема замкнутой системы при действии задающего воздействия и равенстве 0 возмущающего воздействия
В данном случае, выходной величиной будет E(s) :
E(s) = G(s)-Y(s) = G(s)-E(s)* W1*W2*W3*W4*W6*W7
Тогда,
E(s) =
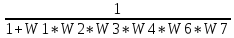 * G(s)
* G(s)
Передаточная функция замкнутой системы по ошибке :
ФE(s)
=
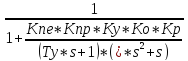 =
=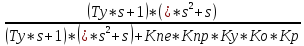
Подставив значения, получим:
ФE(s)
=
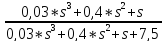
3.4. Передаточную функцию замкнутой системы по ошибке при действии возмущающего воздействия и равенстве 0 задающего воздействия
W5



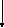
MH(s)
G(s) E(s) Y(s)
W1*W2*W3*W4





W6*W7



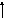
Y(s)
В данном случае :
E(s) = G(s)-Y(s) = G(s) - E(s)* W1*W2*W3*W4*W6*W7 + MH(s)* W5*W6*W7 , где G(s)=0
Тогда,
E(s) =
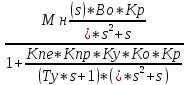 =
=
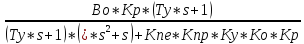 *Мн(s)
*Мн(s)
Передаточная функция замкнутой системы по ошибке :
ФE(s)
=

Подставив значения, получим:
ФE(s)
=

4.Вычислить временные характеристики
4.1.Рассмотреть САУ при равенстве нулю возмущающего и g(t)=const при нулевых начальных условиях y(0)=0 y'(0)=0 y"(0)=0
Математическая модель САУ :
Y(s)
= G(s)*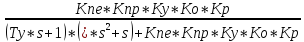 -
MH(s)*
-
MH(s)*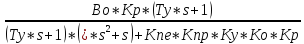
Ty*To*s3*Y(s) + (Ty+To)*s2*Y(s) + s*Y(s) + Кпе*Кпр*Ку*Ко*Кр*Y(s) = Кпе*Кпр*Ку*Ко*Кр*G(s) -
–Bo*Kp*(Ty*s+1)*MH(s)
Подставим
значения и применим обратное преобразование
Лапласа, где S=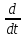 :
:
0,03*y```(t)
+ 0.4*y``(t) + y`(t) + 7.5*y(t) = 7.5*g(t)
или, разделив на 7,5 , получим:
0,004*y```(t) + 0,05*y``(t) + 0,13*y`(t) + y(t) = g(t)
4.2.С помощью обратного преобразования Лапласа найти переходную и весовую функции
Положим МН(t) = 0, тогда передаточная функция системы равна :
W(s)
=
 или
или
Пусть на вход системы подается воздействие g(t) = 1(t) – скачок , тогда при обратном преобразовании Лапласа Y(s) будет изображением переходной функции H(s), тогда :

H(s)
=
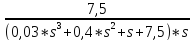 ,
где
g(t) = 1(t)
,
где
g(t) = 1(t)
 G(s) =
G(s) =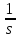
Запишем характеристическое уравнение :
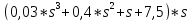 =
0
=
0
Найдем его корни :
S1 = 0;
 =
0 или a
=
0 или a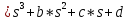 = 0
= 0
Сделаем
замену, s=
y
-
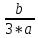
p
=
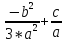 ; q =
; q =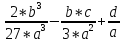
Q
=
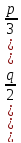 =1860
=1860
Т.к.
Q
> 0, то α =
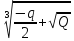 ;β
=
;β
=
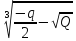
y2 = α + β ;
y3,4
=
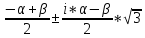 ;
;
y2 = -7,832;
y3 = 3,7 +4,482*i ;
y4 = 3,7 – 4,482*i ;
Тогда,
S2
= y2
-
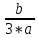 = -12,277 ;
= -12,277 ;
S3
= y3
-
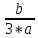 = -0,528 + 4,482*i ;
= -0,528 + 4,482*i ;
S4
= y4
-
 = -0,528 - 4,482*i ;
= -0,528 - 4,482*i ;
Тогда,
H(s) =
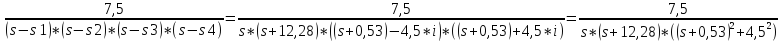
Используя обратное преобразование Лапласа найдем переходную функцию:
h(t)
=

|
t |
h(t) |
|
0 |
0 |
|
1 |
0,058 |
|
2 |
0,032 |
|
3 |
0,02 |
|
6 |
0,032 |
|
10 |
0,03 |
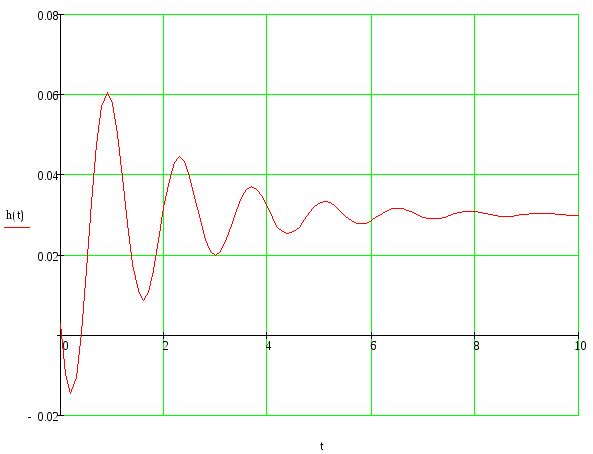
График переходной функции
Зная переходную функцию, найдем функцию веса:
w(t) = h`(t)
w(t)
= 0,03* + 0,002*
+ 0,002*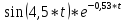 - 0,04*
- 0,04*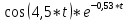 +0,45*
+0,45*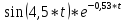 +0,055*
+0,055*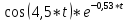
5.Частотные характеристики
5.1.Афчх
Т.к.
Y(s)
= G(s)*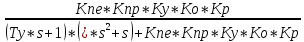 -
MH(s)*
-
MH(s)*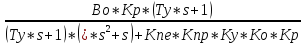
то, передаточная функция САУ по задающему воздействию:
W(s)
=
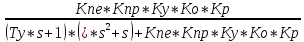 =
=

Подставим s=j*ω, тогда получим частотную характеристику :
W(j*ω)
=
 =
=
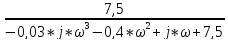 =
=
=
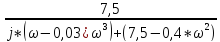 =
=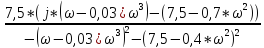 =
=
=
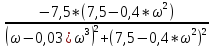 - j*
- j*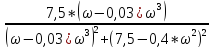
Таким образом получили АФЧХ системы:
W(j*ω)
=
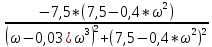 - j*
- j*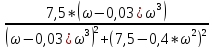
где
U(ω)
= ReW(j*ω)
=
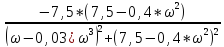 -
действительная
частотная характеристика
-
действительная
частотная характеристика
V(ω)
= ImW(j*ω)
=
 –
мнимая
частотная характеристика
–
мнимая
частотная характеристика
|
ω |
U(ω) |
V(ω) |
|
0 |
1 |
0 |
|
1 |
1,04 |
-0,142 |
|
2 |
1,17 |
-0,35 |
|
3 |
1,46 |
-0.82 |
|
4 |
1.48 |
-2.81 |
|
5 |
-2.4 |
-1.2 |
|
∞ |
→ 0 |
→ 0 |
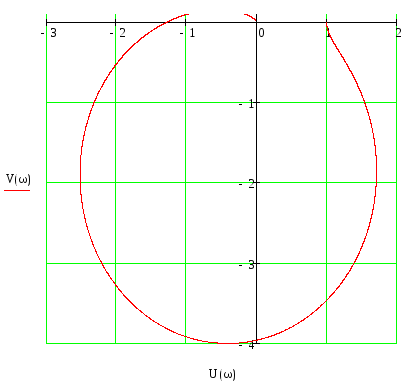 График
АФЧХ
График
АФЧХ
5.2.АЧХ
Амплитудно – частотная характеристика :
А(ω)
=
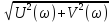
A(ω)
=
 =
=
=
 =
=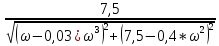
A(ω)
=
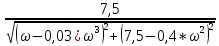
|
ω |
A(ω) |
|
0 |
1 |
|
1 |
1,05 |
|
3 |
1,68 |
|
5 |
2,68 |
|
20 |
0,03 |
|
|
→ 0 |
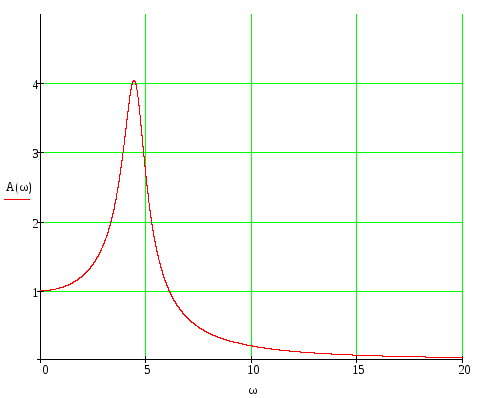
График АЧХ
5.3.ФЧХ
ФЧХ системы определяется за формулой:
φ(ω)
= arctg ( )
)
φ(ω)
= arctg(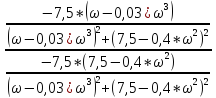 )
= arctg(
)
= arctg(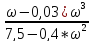 )
)
φ(ω)
= arctg(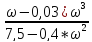 )
)
|
ω |
φ(ω) |
|
0 |
0 |
|
1 |
-0,14 |
|
5 |
0,46 |
|
10 |
-0,55 |
|
20 |
-0,96 |
|
|
-1,1 |
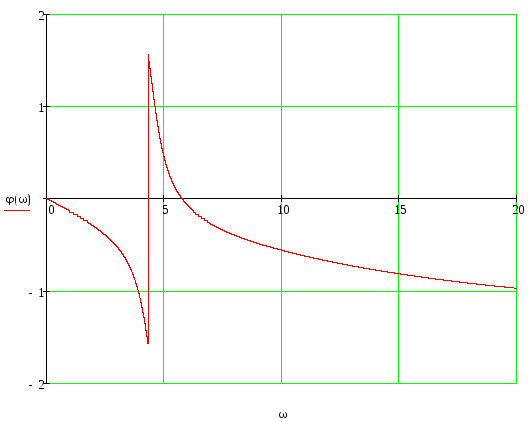
График ФЧХ