3.2 Расчет основных параметров редуктора
Предварительное передаточное отношение редуктора выбирается исходя из формулы
Необходимость определения основных параметров редуктора вызвана тем, что он входит в кинематическую цепь привода и во многом определяет как массогабаритные показатели, так и динамические. Кроме того, как привило, редуктор является тем звеном привода, на котором компонуются элементы, связанные с механикой и перемещениями – двигателя. Первичные измерительные преобразователи называются обычно механическим узлом привода. [1]
Для редуктора с цилиндрическими зубчатыми колёсами целью расчёта является определения числа пар зубчатых колёс n, количества зубьев каждого колеса zj, модуля m, габаритов зубчатых колёс – диаметра αj и ширины bj.
Число пар n зубчатых колёс определяется по формуле
(3.6)
Значение n округляем до ближайшего меньшего (n=3). Затем определяется передаточное число пар зубчатых колёс из соображений минимальности момента инерции редуктора. Поэтому передаточные числа первых двух пар выбираются в пределах 2–3, а третьей и последующих – в пределах 4–8.
из
этого видно число пар (i)=4 и передаточные
числа 2–2–7–6.
Рисунок 3.2 Схема редуктора
Определим
число зубьев ведущих колес:
Для определения количества зубьев остальных колёс воспользуемся формулой
z2j = ij * z2j-1, (3.7)
где
Для определения размеров зубчатых колёс предварительно нужно определить модуль m по выражению:
,
(3.8)
где Mнм – максимальный момент нагрузки на выходном зубчатом колес; kβ – коэффициент ширины зуба; σ – допустимое напряжение в материале зубчатого колеса при расчёте на выносливость; z2n – количество зубьев выходного зубчатого колеса.
По известному значению модуля определяется диаметр зубчатых колёс
di = m*zi, (3.9)
где
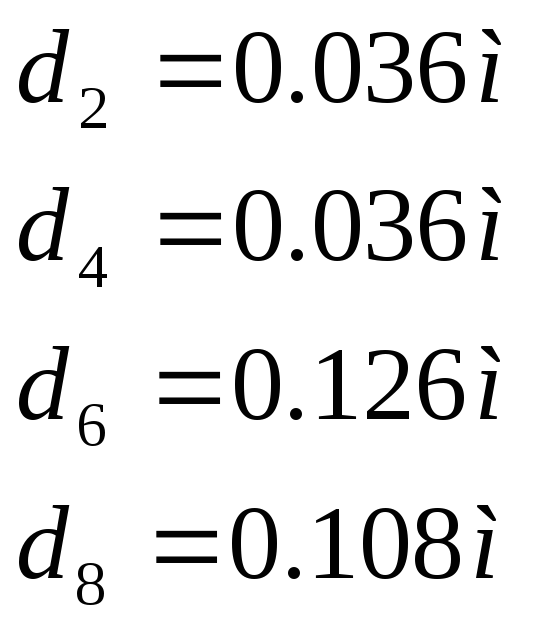
Ширину зубчатых колёс вычисляют по формуле:
,
(3.10)
где κβ - коэффициент ширины зуба 8; m – было заданно в 3.9.
Полагая, что зубчатые колёса сплошные и одинаковой ширины, момент инерции редуктора можно определить по формуле где ρ – удельная плотность материала зубчатых колёс (7,8*10³ кг/м³);
π=3.14; получаем
(3.11)
3.3 Передаточная функция исполнительного механизма
Исполнительный механизм представляет собой сложное электромеханическое звено, передаточная функция которого должна определяться с учётом всех его составляющих и особенностей функционирования.
При построении передаточной функции ИМ следует опираться на какой-либо конкретный способ регулирования скорости вращения двигателя. В настоящем проекте будем считать, что регулирование скорости двигателя постоянного тока независимого возбуждения (ДПТ НВ) производится изменением напряжения в якорной цепи.
Привод антенн характеризуется значительными моментами инерции рабочих органов. Кроме того, выходные валы ПМ обычно связываются с РО различными муфтами, которые имеют вполне определенную (не бесконечно большую) конструкционную жесткость Су, которая представляется как коэффициент упругого скручивания вала редуктора. Реальные величины Су лежат в диапазоне (10² – 10³) Нм/рад. Указанные обстоятельства требуют учета конечной жесткости в математической модели привода. [1]
Структурная схема ИМ приведена на рисунке 3.3, где Км – коэффициент пропорциональности ИД между напряжением и моментом; Кn – коэффициент пропорциональности ИД между скоростью и ЭДС.
кг*м2,
(3.13)
где; J'д = (Jд+Jq)*i² – момент инерции ИД и ПМ, приведенный к выходному валу редуктора; i – передаточное отношение редуктора; η – КПД редуктора; Су – коэффициент упругого скручивания; Jн – момент инерции нагрузки; Jд – момент инерции ротора двигателя; р – оператор преобразования Лапласа.
Рисунок 3.3 Структурная схема ИМ с упругим валом
Передаточная функция ИМ имеет следующий вид:
,
(3.14)
где
Таким образом, подставляя, все найденные значения полинома передаточная функция исполнительного механизма приобретает, следующий вид:
После разложения передаточной функции
Откуда следует, что постоянные времени и частоты, необходимые в дальнейшем равны
