
- •010700 Физика
- •1. Цели освоения дисциплины
- •2. Место дисциплины в структуре ооп бакалавриата
- •3. Требования к результатам освоения содержания дисциплины
- •4. Структура и содержание дисциплины (модуля)
- •5. Содержание разделов (тем) дисциплины
- •Раздел 1. Понятие линейного векторного пространства.
- •Раздел 2. Общие системы линейных уравнений. Однородные системы.
- •Раздел 3. Линейная зависимость и независимость векторов. Ранг и базис векторов.
- •Раздел 4. Матрицы.
- •Раздел 5. Определители.
- •Раздел 6. Элементы векторной алгебры в аналитической геометрии.
- •Раздел 7. Координатный метод в геометрии.
- •Раздел 8. Прямая и плоскость.
- •Раздел 9. Кривые и поверхности второго порядка.
- •Раздел 10. Подпространства линейного пространства. Изоморфизм векторных пространств.
- •Раздел 11. Линейные операторы.
- •Раздел 12. Евклидово пространство (вещественное и комплексное).
- •Раздел 13. Линейные операторы, действующие в евклидовом пространстве.
- •Раздел 14. Билинейные и квадратичные формы.
- •Раздел 15. Элементы теории групп.
- •6. Образовательные технологии:
- •7. Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины и учебно-методическое обеспечение самостоятельной работы студентов
- •I семестр
- •II семестр
- •Вопросы к коллоквиумам
- •I семестр
- •II семестр
- •Примерные варианты контрольных работ
- •I семестр (3 варианта из 6)
- •II семестр (2 варианта из 10)
- •8.Учебно-методическое и информационное обеспечение дисциплины (модуля)
- •9. Материально-техническое обеспечение дисциплины (модуля)
- •2.Тематические тесты алгебре и аналитической геометрии
- •1. Матрицы и определители Тест1.
- •2. Системы линейных уравнений Тест 1
- •3. Векторная алгебра Тест 1
- •4. Прямая линия на плоскости Тест 1
- •1. Укажите, какие из следующих уравнений определяют прямую линию:
- •Прямая в пространстве Тест 1
- •Лабораторная работа
- •Ход выполнения работы
- •11. Вывод уравнения прямой по двум точкам
- •1V. Вывод уравнений прямой линии в пространстве
- •V. По результатам проведенного исследования заполните следующую таблицу. Различные уравнения прямой на плоскости и в пространстве
- •Дидактические материалы для организации самостоятельной работы студентов физического факультета по дисциплине « Линейная алгебра и аналитическая геометрия
- •1. Литература, рекомендуемая для изучения дисциплины
- •1.1. Основная литература
- •1.2. Дополнительная литература
- •2. Содержание курса линейной алгебры и аналитической геометрии
- •3. Задания для самостоятельной работы на первый семестр
- •3.1.Темы для самостоятельного изучения
- •3.2. Вопросы к коллоквиуму
- •3.3. Индивидуальная домашняя контрольная работа №1
- •3.4. Индивидуальная домашняя контрольная работа №2
- •3.5.Примерные варианты контрольной работы по аналитической геометрии Варианты № 1
- •Вариант №2
- •Вариант №3
- •4. Задания для самостоятельной работы на второй семестр
- •4.1. Темы для самостоятельного изучения
- •4.2. Вопросы к коллоквиуму
- •4.3. Индивидуальное домашнее задание № 3
- •5.4. Примерные варианты 20 - минутной самостоятельной работы по теме "Линейные преобразования"
- •5.5 Примерные варианты контрольной работы по линейной алгебре
- •6. Программа экзамена по курсу "аналитическая геометрия и линейная алгебра"
- •I семестр
- •II семестр
4.3. Индивидуальное домашнее задание № 3
-
Является ли линейным подпространством соответствующего векторного пространства каждая из следующих совокупностей векторов:
-
Все векторы п - мерного векторного пространства, координаты которых - целые числа?
-
-
Все векторы плоскости, каждый из которых лежит на одной из осей координат Ох и Оу?
1.3. Все векторы плоскости, концы которых лежат на одной прямой (начало любого вектора предполагается совпадающим с началом координат)?
-
Все векторы плоскости, начала и концы которых лежат на данной прямой?
-
Все векторы трехмерного пространства, концы которых не лежат на данной прямой?
-
Все векторы плоскости, концы которых лежат в первом четверти системы координат?
-
Все векторы из
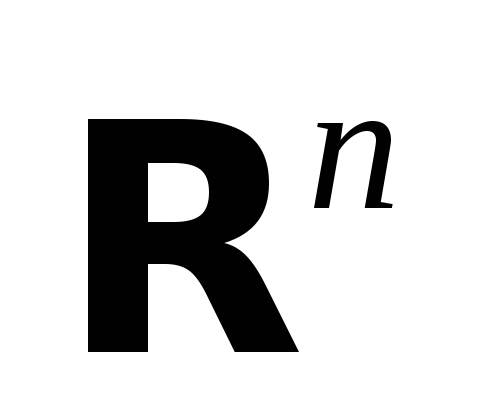 ,
координаты
которых удовлетворяют уравнению
,
координаты
которых удовлетворяют уравнению
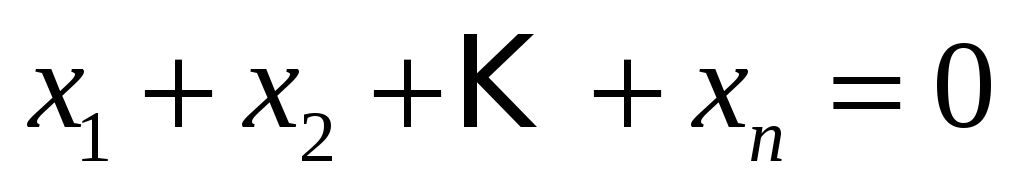 ?
? -
Все векторы из
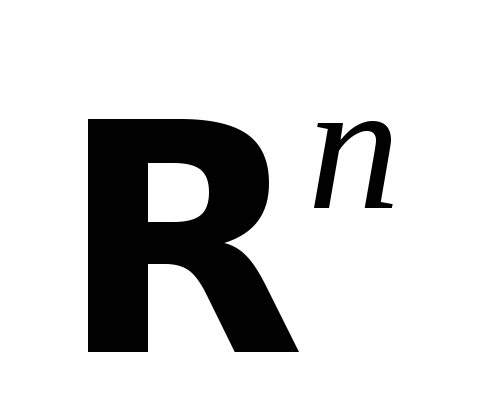 ,
координаты
которых удовлетворяют уравнению
,
координаты
которых удовлетворяют уравнению
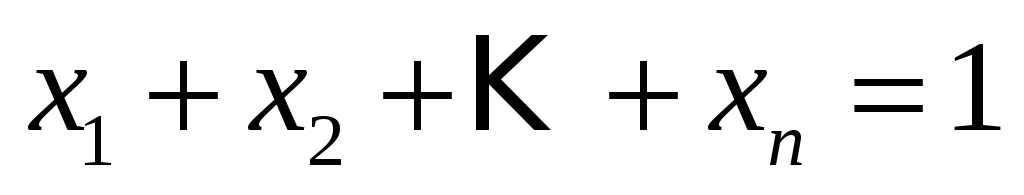 ?
? -
Все векторы, являющиеся линейными комбинациями данных векторов
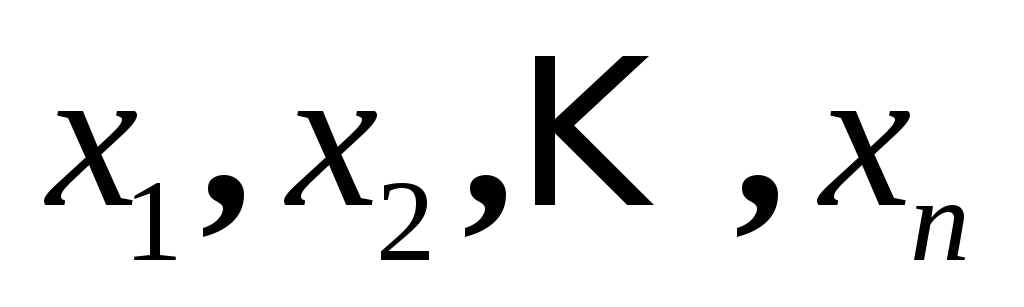 из
из
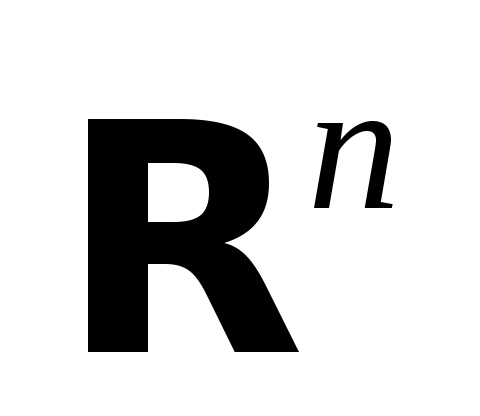 ?
?
-
Все п - мерные векторы, у которых первая и последняя координаты равны между собой.
-
Все п - мерные векторы, у которых координаты с четными номерами равны нулю.
-
Все п - мерные векторы, у которых координаты с четными номерами равны между собой.
-
Множество всех симметричных матриц порядка я относительно обычных операций сложения матриц и умножения их на действительное число ?
-
Множество всех невырожденных матриц
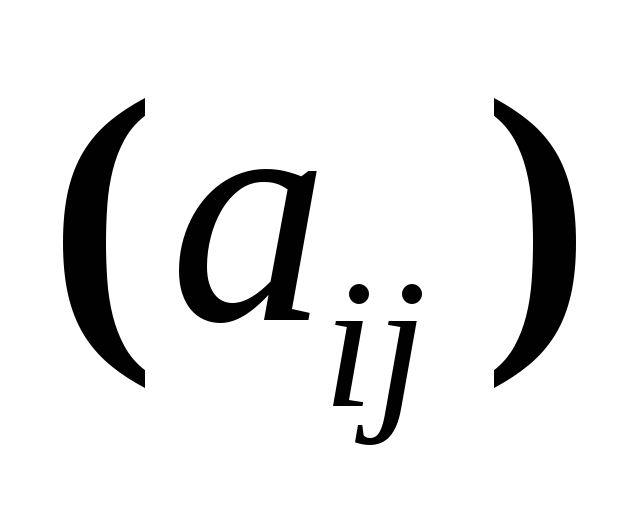 порядка п,
если сумма
их определена так:
порядка п,
если сумма
их определена так:
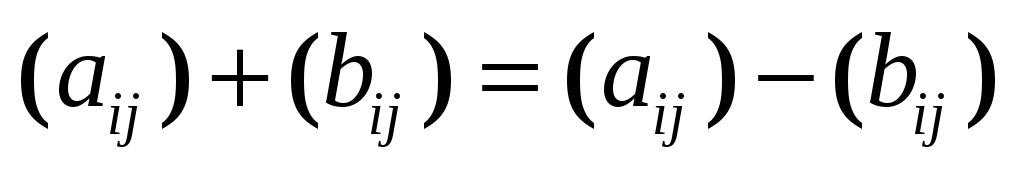 .
а произведение на число -обычным
образом ?
.
а произведение на число -обычным
образом ?
-
Множество всех кососимметричных матриц, т.е. матриц
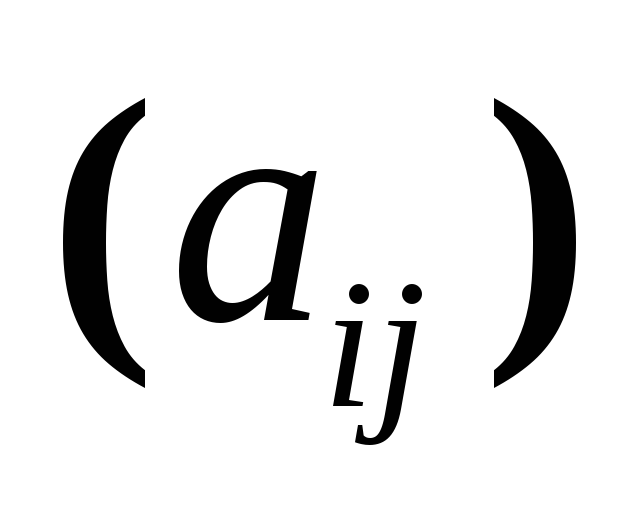 удовлетворяющих
условию
удовлетворяющих
условию
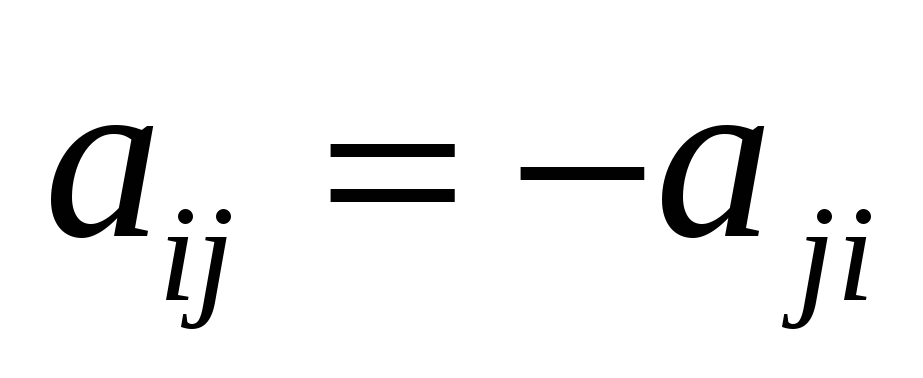 относительно обычных операций сложения
матриц и умножения их на число?
относительно обычных операций сложения
матриц и умножения их на число? -
Множество кососимметричных матриц, если их сумма и произведение определены так, как в задаче 1.14?
-
Множество решений любой системы однородных линейных уравнений с п переменными ранга 2?
-
Множество всех четных функций, заданных на [-1, 1] , если суммой двух функций a=f(t), b=g(t) считается функция f(t)g(t) , а произведение на число определяется обычным образом?
-
Множество всех нечетных функций, заданных на [-1, 1], если сумма двух функций и произведение на число определены так же, как в задаче 1.18.
-
Множество всех дифференцируемых функций с обычными операциями сложения и умножения их на действительное число, если суммой двух функций считается функция f(t)g(t)?
-
Множество диагональных квадратных матриц порядка n.
-
Множество функций монотонно возрастающих на [а, b].
-
Множество функций монотонных на [a, b].
-
Множество вырожденных квадратных матриц порядка n.
-
Множество функций на [a, b] таких, что f(a)=0.
2. Найти какой-нибудь базис и определить размерность линейного пространства решений однородной системы, основная матрица которой имеет вид:
2.1. 2.2 . 2.3.
 ;
;


2.4. 2.5 . 2.6.



2.7. 2.8 . 2.9.



2.10. 2.11. 2.12.



2.13. 2.14 . 2.15.



2.16. 2.17. 2.18.



2.19. 2.20. 2.21.



2.22. 2.23. 2.24.



2.25.
 .
.
3.Найти координаты
вектора
![]() в базисе
в базисе
![]() ,
если он задан в базисе
,
если он задан в базисе
![]() :
:
3.1. 3.2.
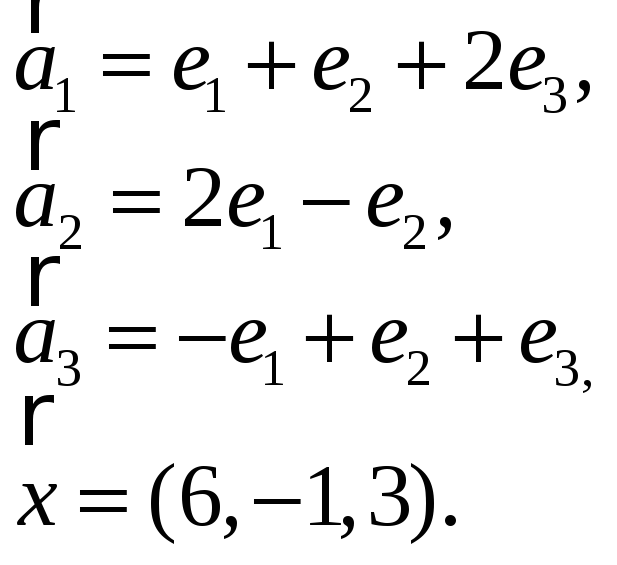
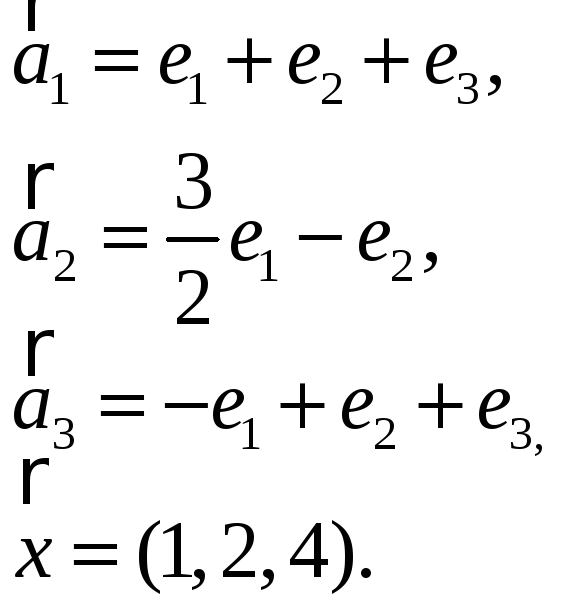
3.3. 3.4.
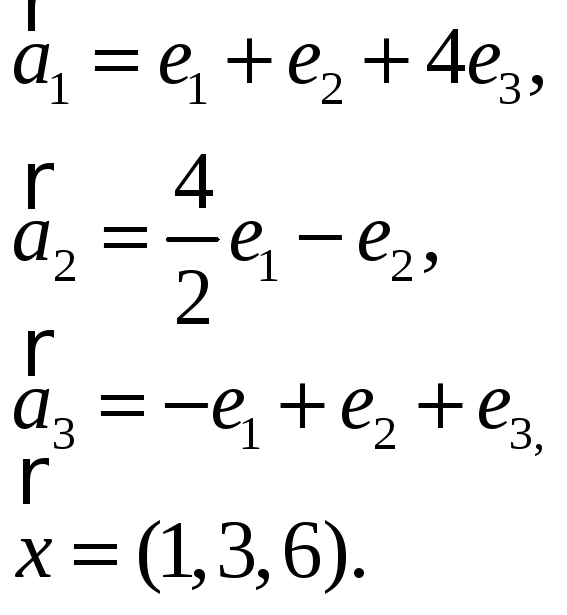

3.5. 3.6
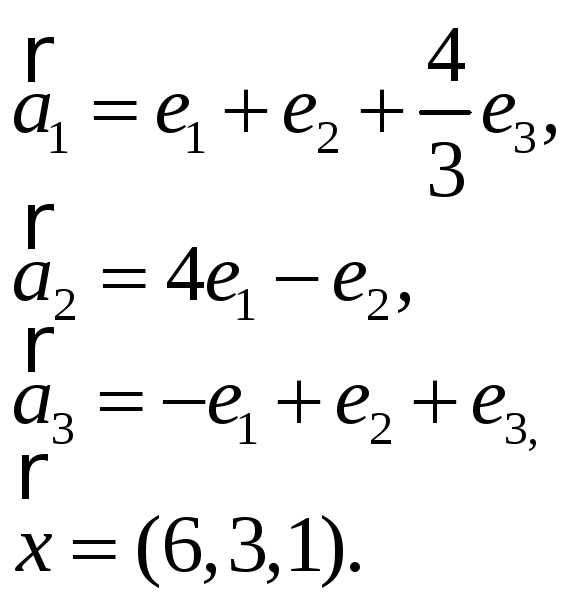
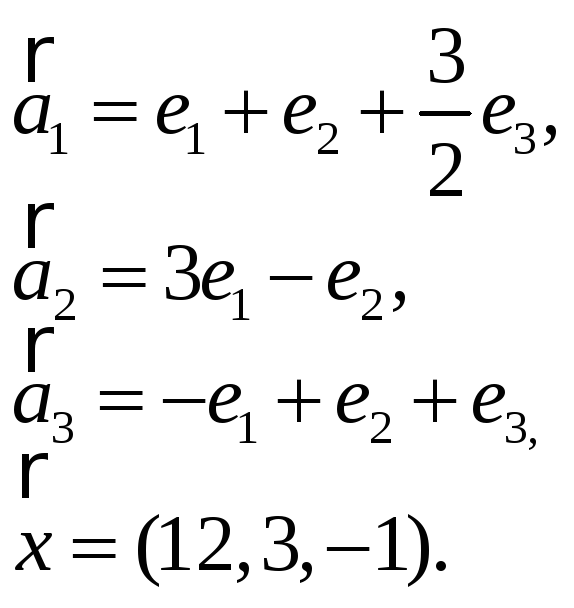
-
3.8.
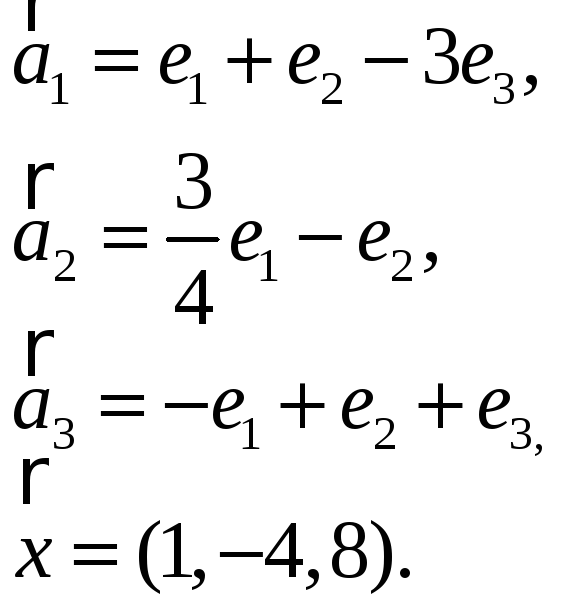
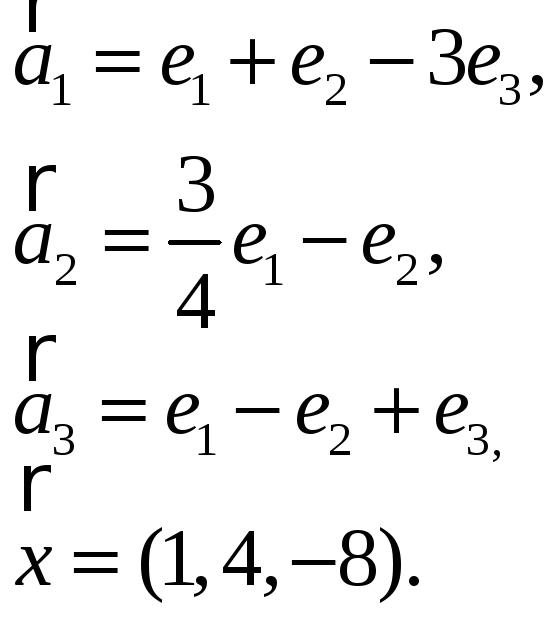
3.9. 3.10.
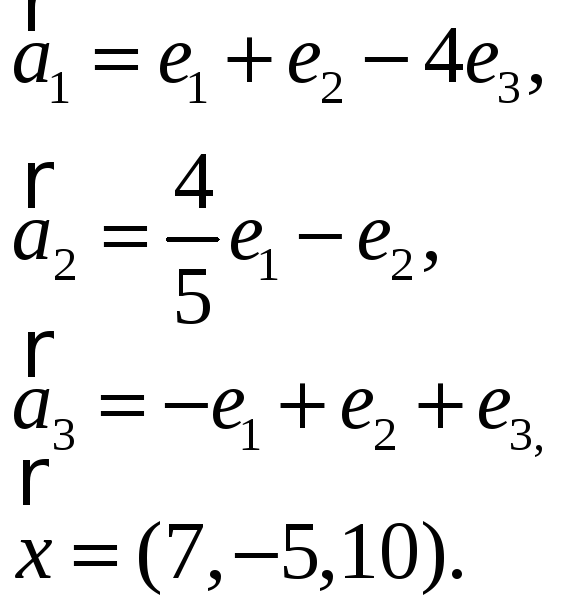
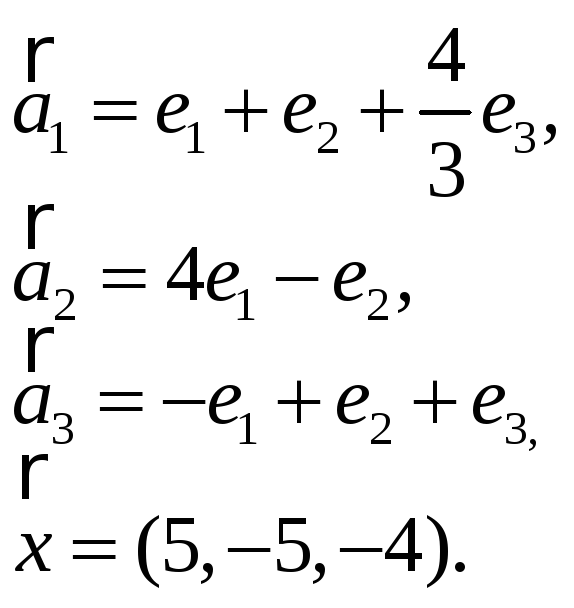
3.11. 3.12.
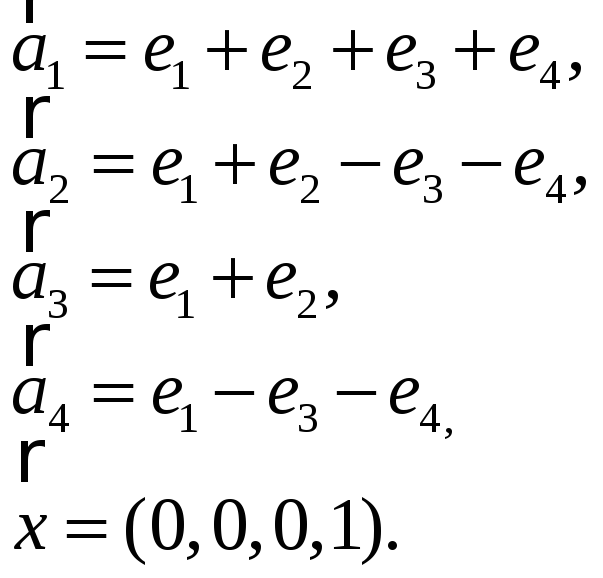

3.13. 3.14.
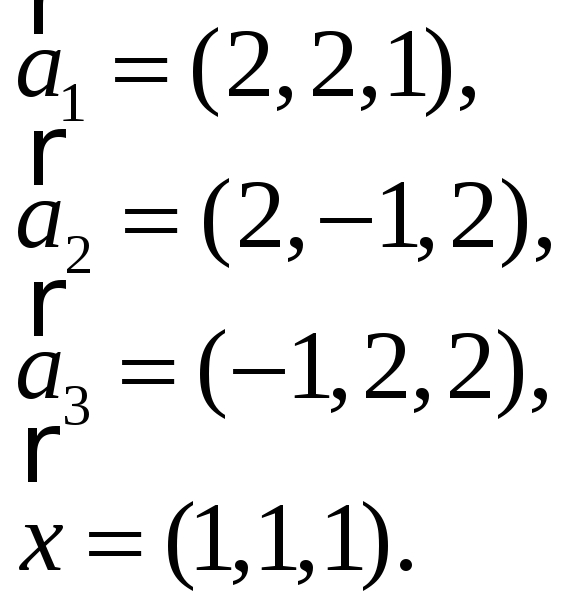
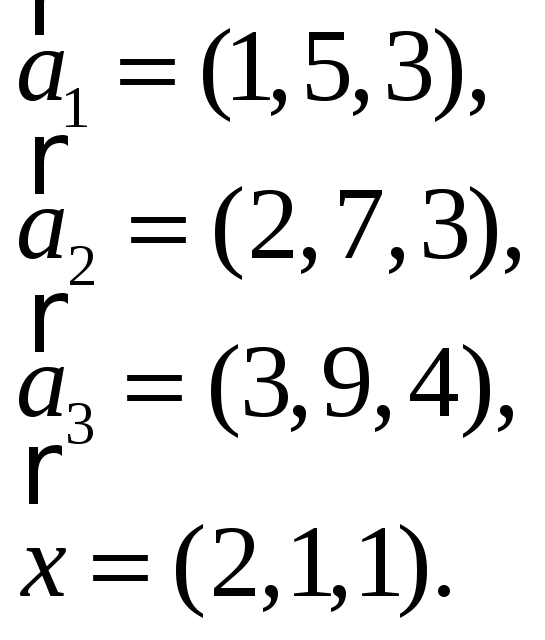
3.15. 3.16.
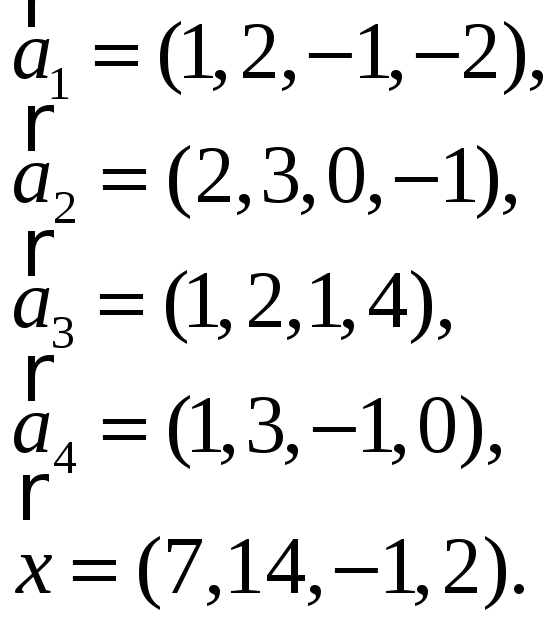
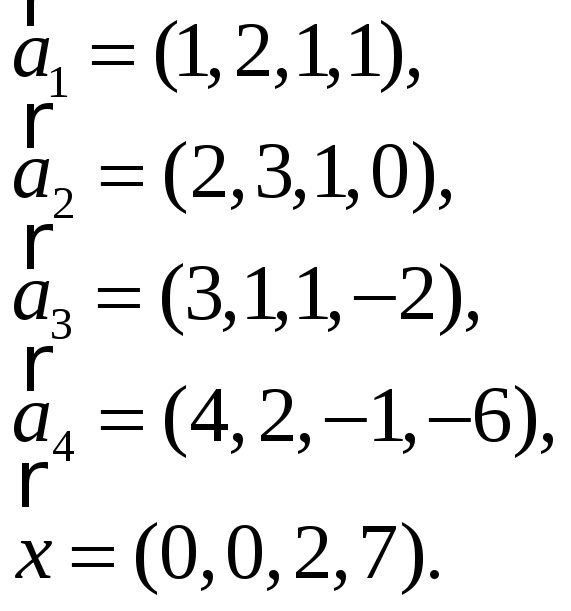
-
3.18.
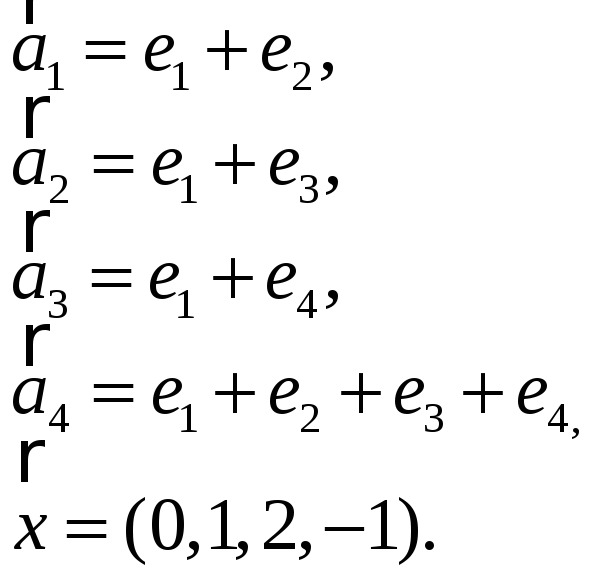
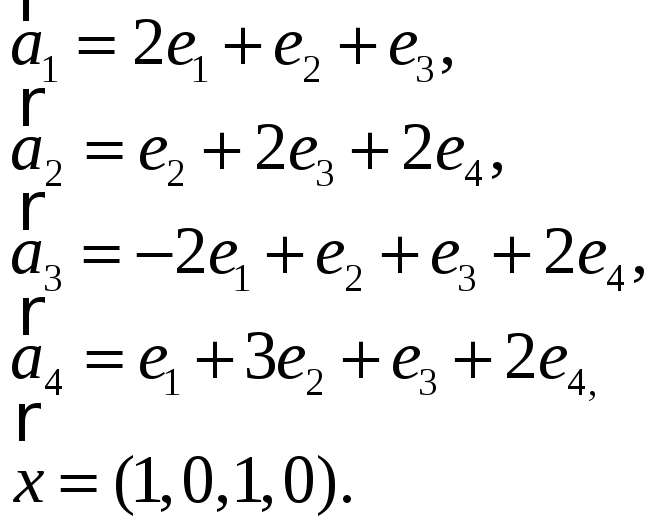
3.19. 3.20
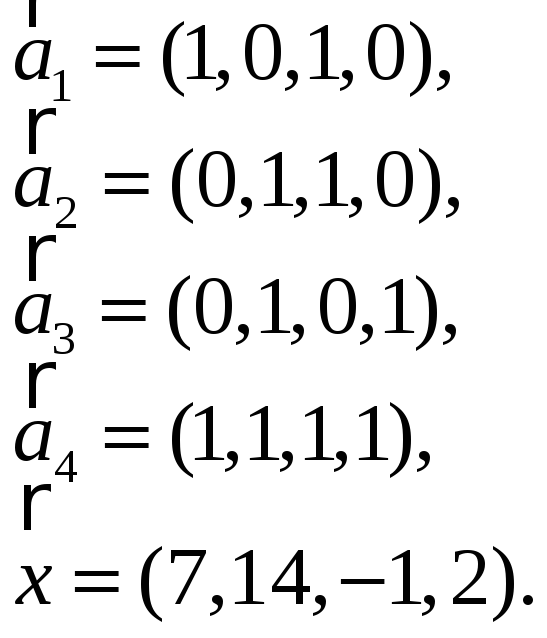
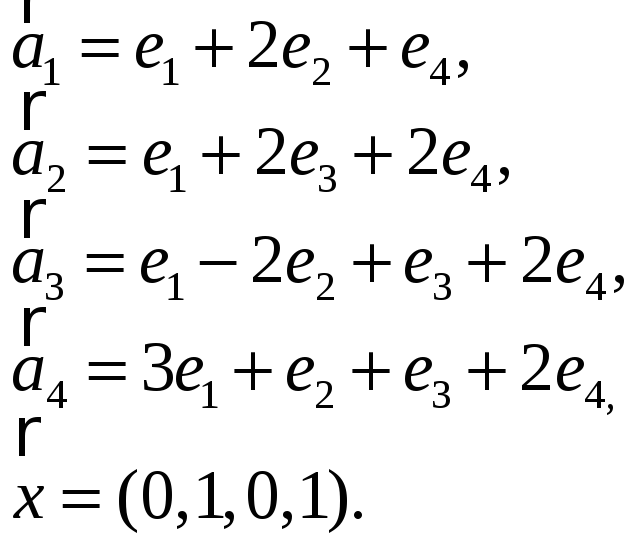
3.21. 3.22.
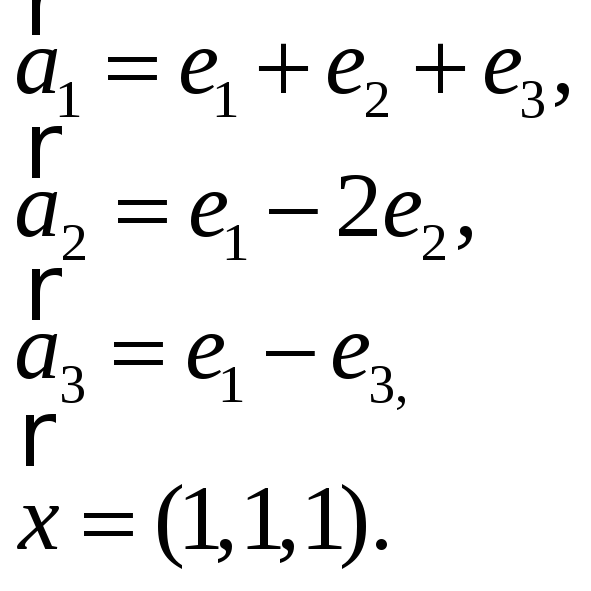

3.23. 3.24.
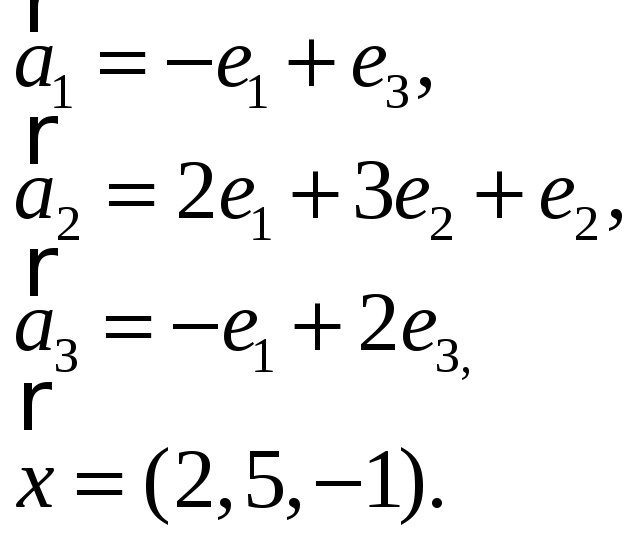
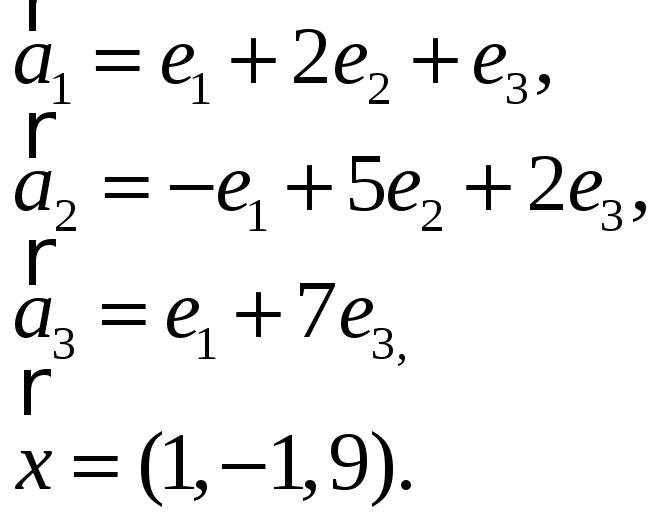
3.25.
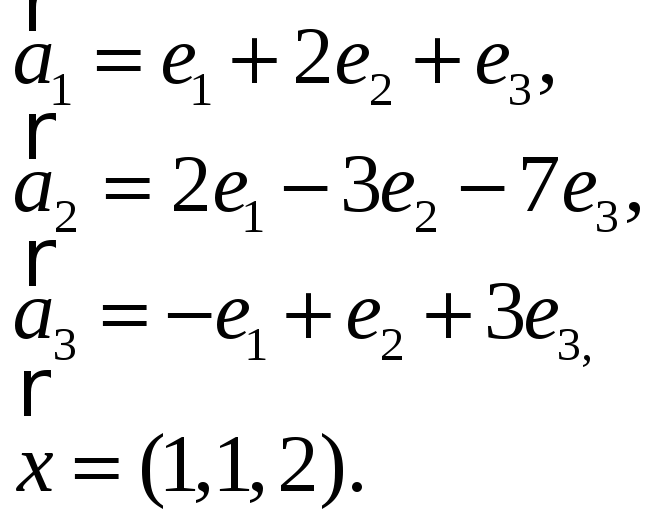
4. Пусть
![]() .
Являются ли линейными следующие
преобразования? Если являются, то
записать матрицу преобразования.
.
Являются ли линейными следующие
преобразования? Если являются, то
записать матрицу преобразования.
4.1.![]() ;
;
![]() ;
;
![]() .
.
4.2.![]() ;
;
![]() ;
;
![]() .
.
4.3.
![]() ;
;
![]() ;
;
![]() .
.
4.4.
![]() ;
;
![]() ;
;
![]() .
.
4.5.
![]() ;
;
![]() ;
;
![]() .
.
4.6.
![]() ;
;
![]() ;
;
![]() .
.
-
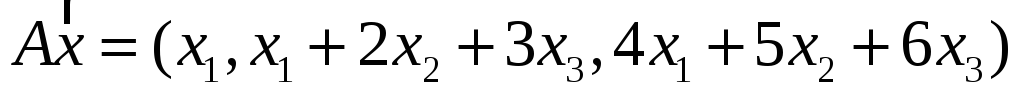 ;
;
![]() ;
;
![]() .
.
4.8.
![]() ;
;
![]() ;
;
![]() .
.
4.9.
![]() ;
;
![]() ;
;
![]() .
.
4.10.
![]() ;
;
![]() ;
;
![]() .
.
-
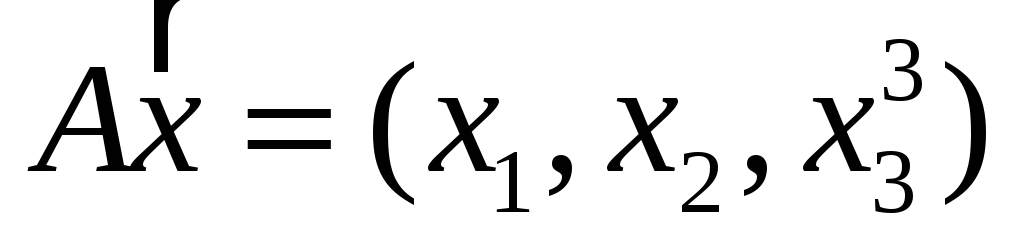 ;
;
![]() ;
;
![]() .
.
4.12.
![]() ;
;
![]() ;
;
![]() .
.
4.13.
![]() ;
;
![]() ;
;
![]() .
.
4.14.
![]() ;
;
![]() ;
;
![]() .
.
4.15.
![]() ;
;
![]() ;
;
![]() .
.
-
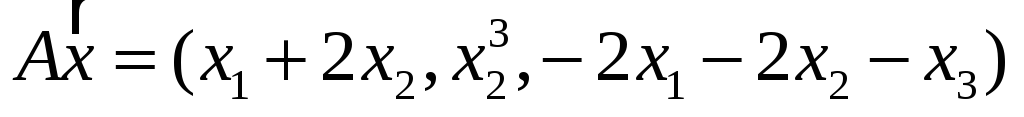 ;
;
![]() ;
;
![]() .
.
-
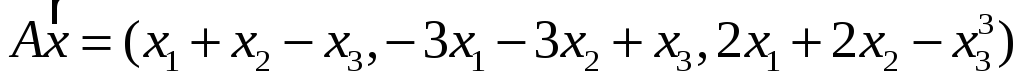 ;
;
![]() ;
;
![]() .
.
-
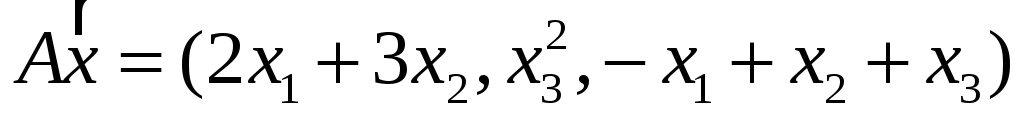 ;
;
![]() ;
;
![]() .
.
-
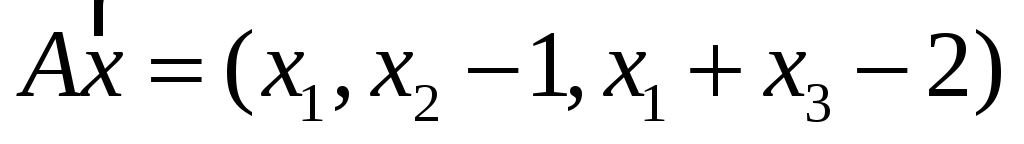 ;
;
![]() ;
;
![]() .
.
-
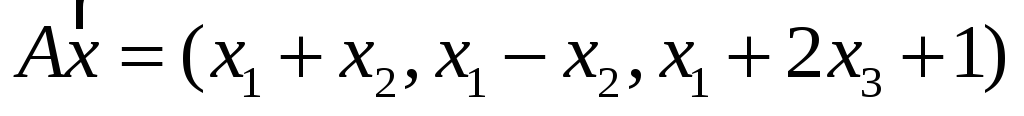 ;
;
![]() ;
;
![]() .
.
-
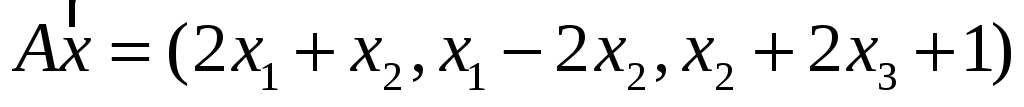 ;
;
![]() ;
;
![]() .
.
-
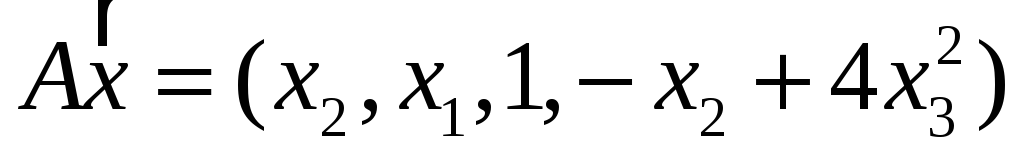 ;
;
![]() ;
;
![]() .
.
-
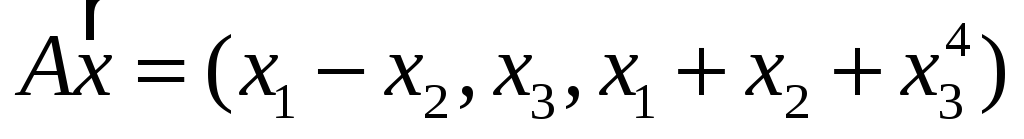 ;
;
![]() ;
;
![]() .
.
-
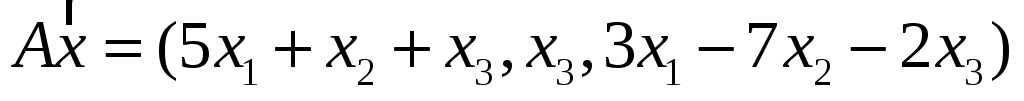 ;
;
![]() ;
;
![]() .
.
-
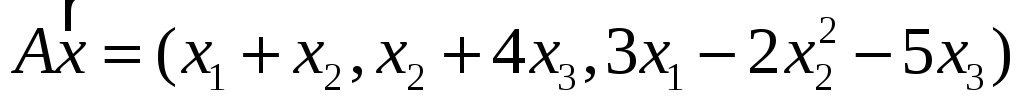 ;
;
![]() ;
;
![]() .
.
5.
Пусть
![]() ,
,
![]() ,
,
![]() .
Найти
.
Найти
5.1.![]() ;
5.2.
;
5.2.
![]() ;
5.3.
;
5.3.
![]() ;
5.4.
;
5.4.
![]() ;
5.5.
;
5.5.
![]() ;
;
5.6.![]() ;
5.7.
;
5.7.![]() ;
5.8.
;
5.8.![]() ;
5.9.
;
5.9.
![]() ;
5.10.
;
5.10.
![]() ;
;
5.11.
![]() ;
5.12.
;
5.12.![]() ;
5.13.
;
5.13.![]() ;
5.14.
;
5.14.
![]() ;
5.15.
;
5.15.![]() ;
;
5.16.![]() ;
5.17.
;
5.17.
![]() ;
5.18.
;
5.18.![]() ;
5.19.
;
5.19.![]() ;
5.20.
;
5.20.![]() ;
;
5.21.
![]() ;
5.22.
;
5.22.![]() ;
5.23.
;
5.23.![]() ;
5.24.
;
5.24.![]() ;
5.25.
;
5.25.![]() .
.
6.Найти
матрицу линейного оператора в базисе
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() ,
если она задана в базисе
,
если она задана в базисе
![]() :
:


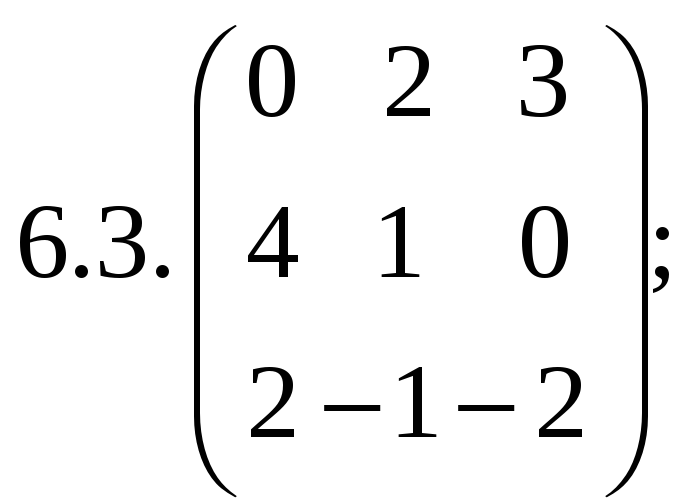
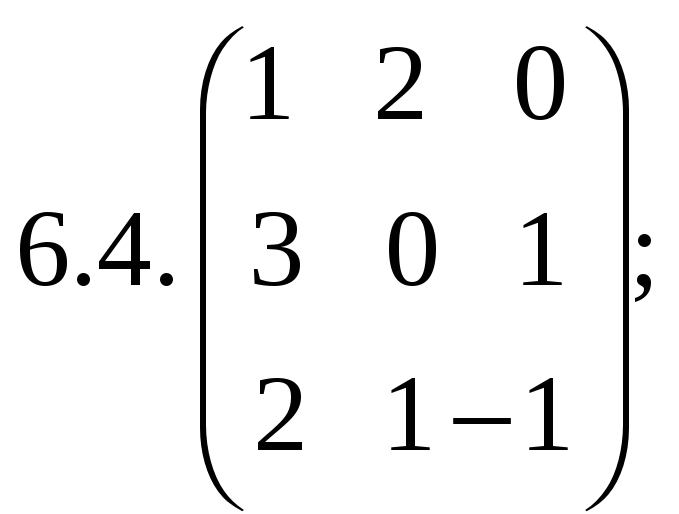
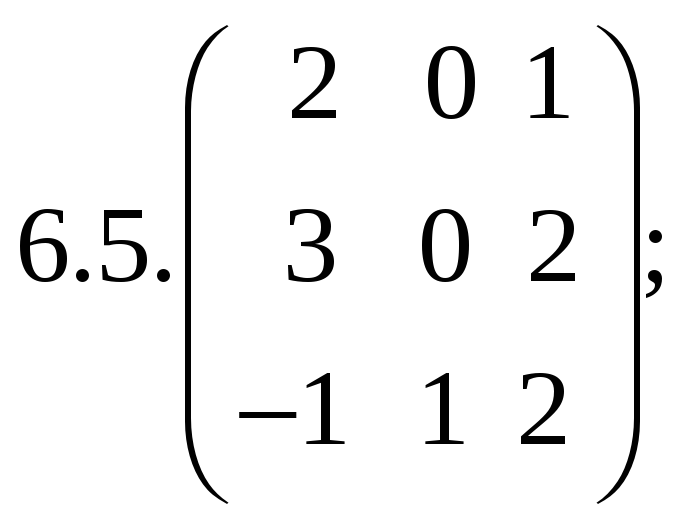
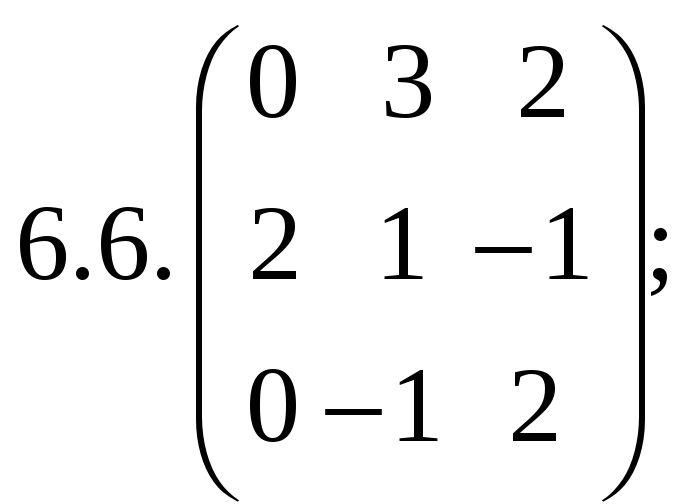
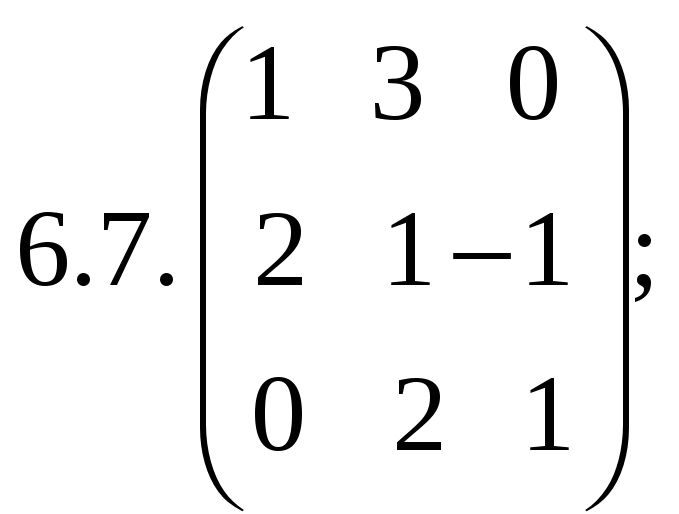
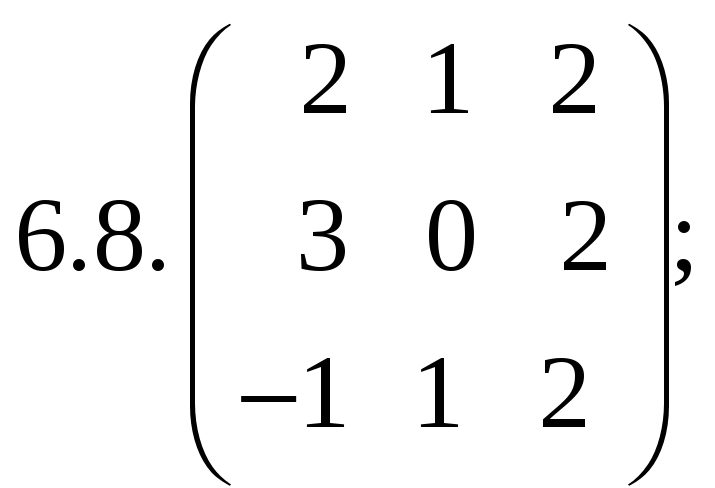
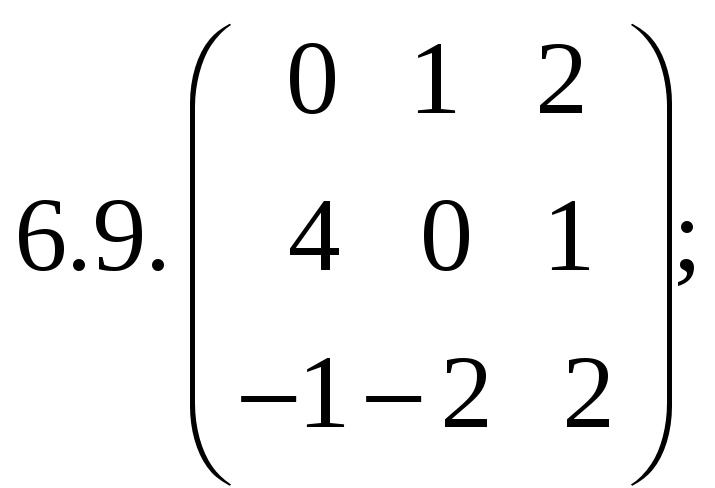
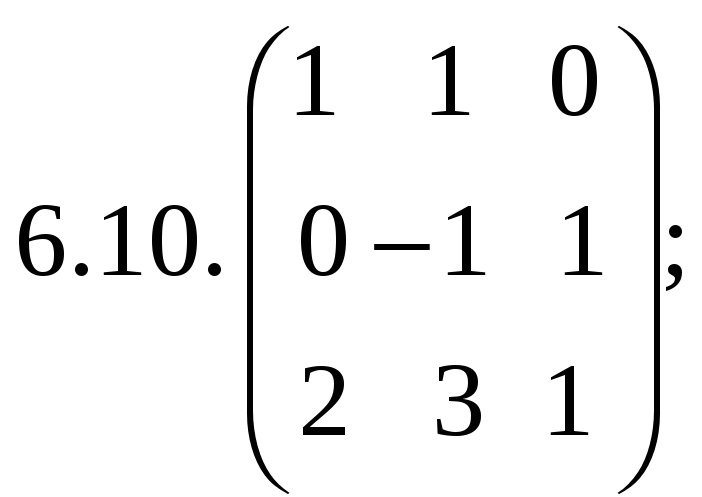
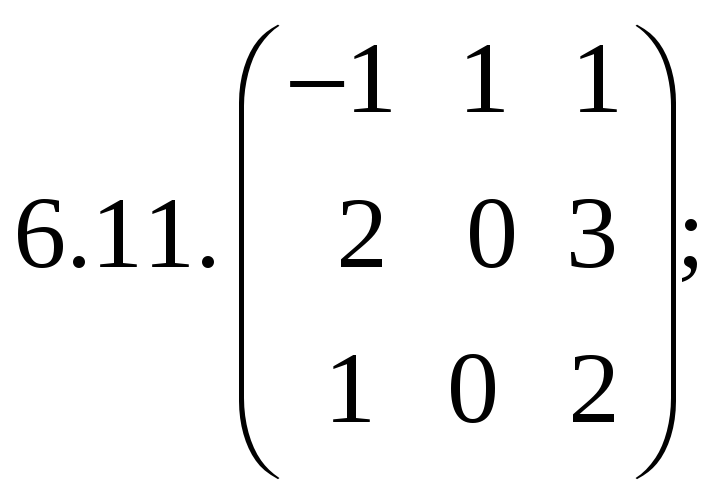
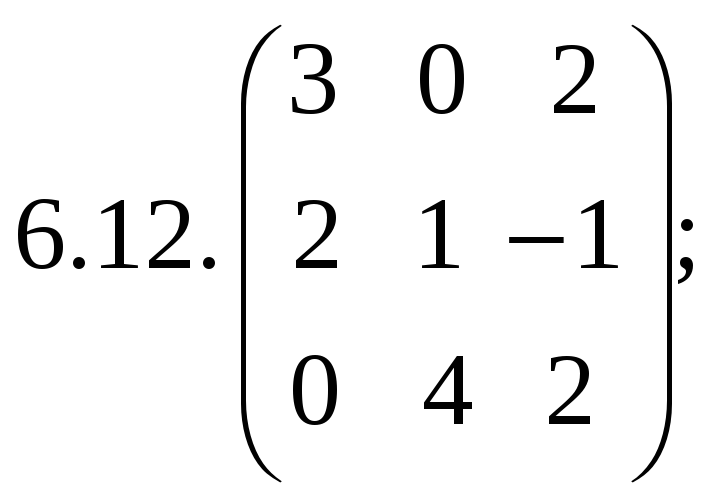
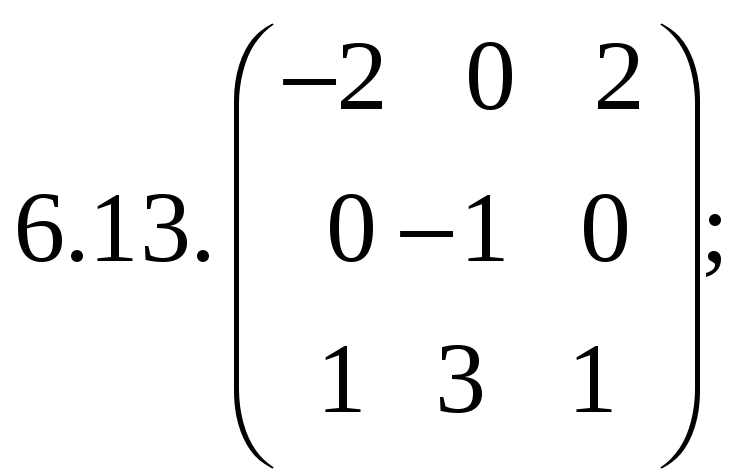
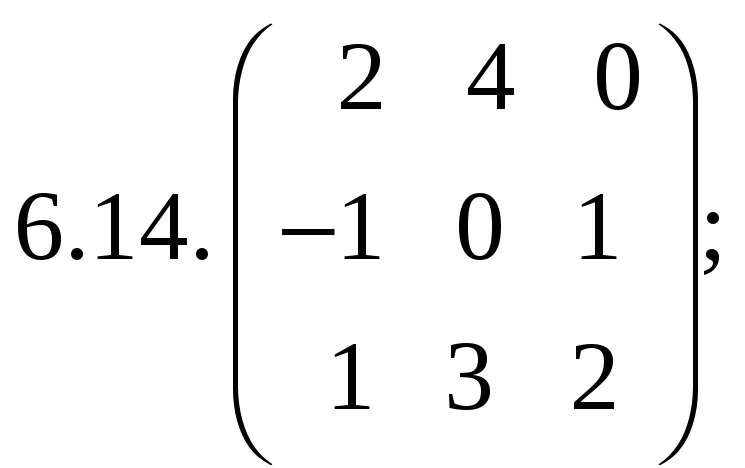
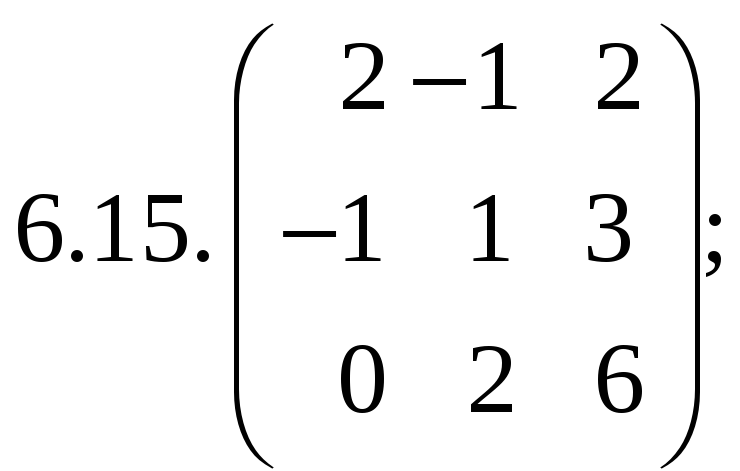
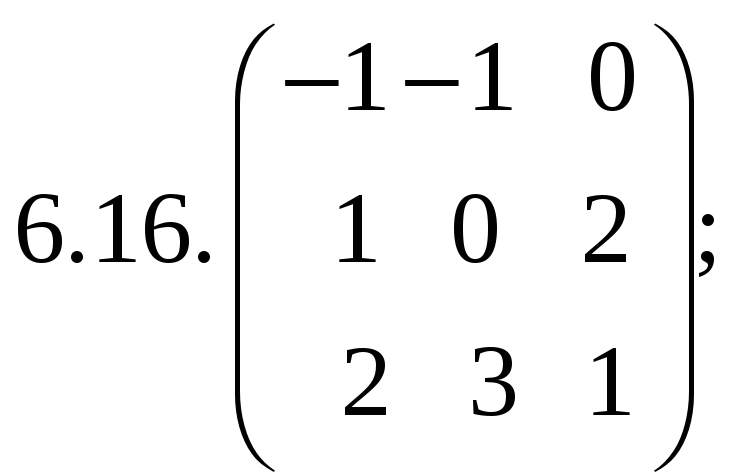
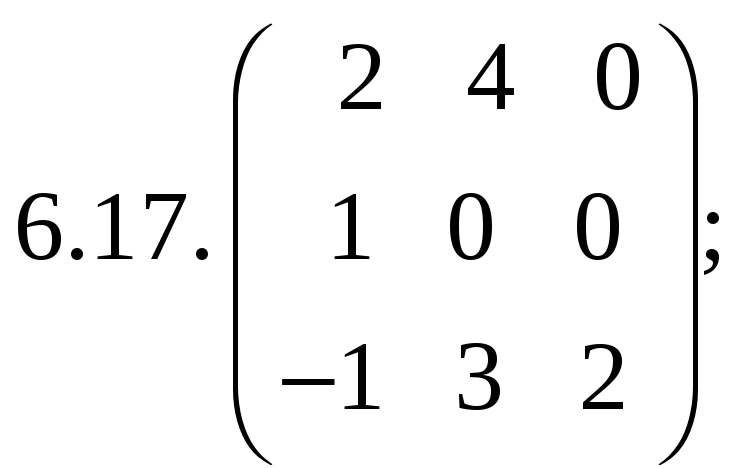
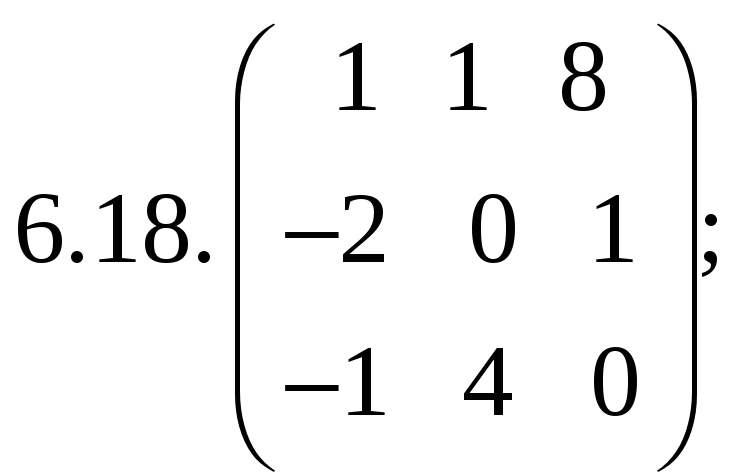
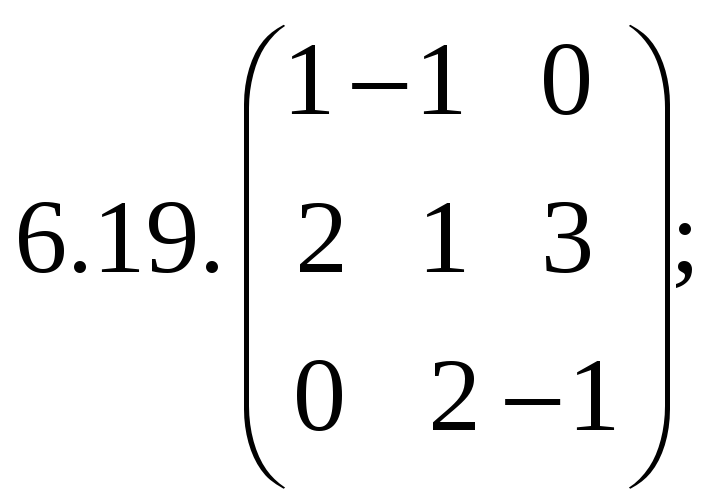
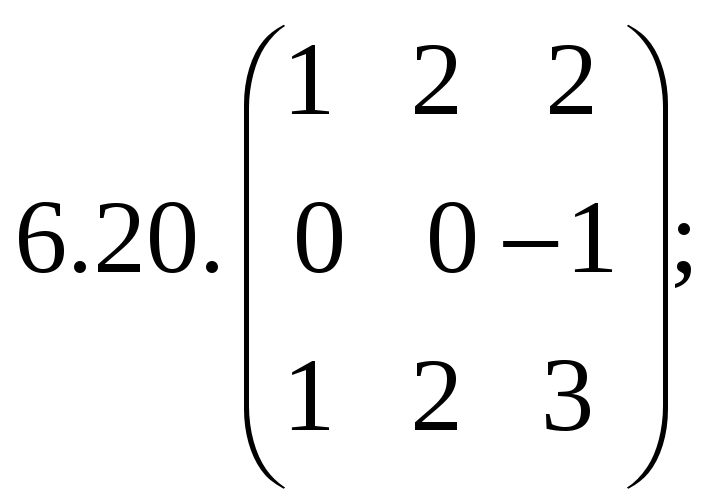
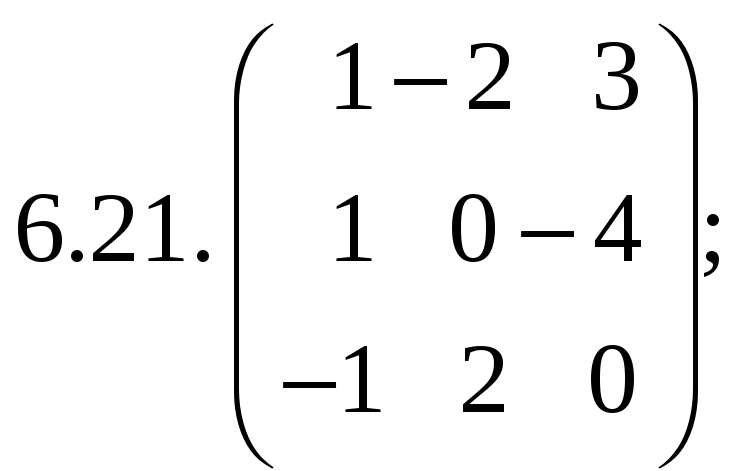
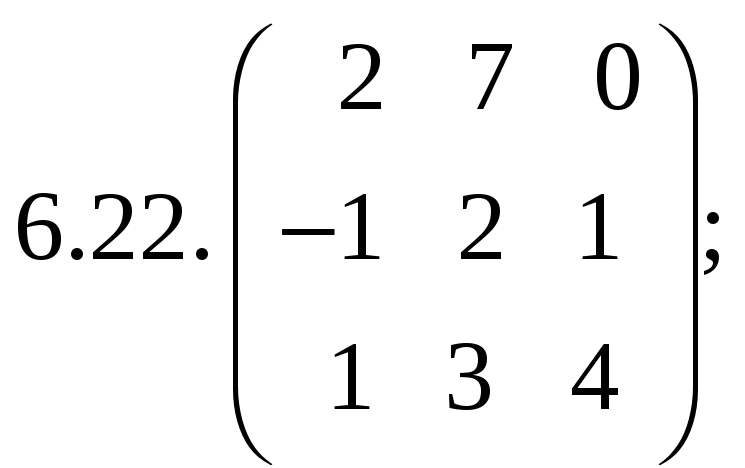

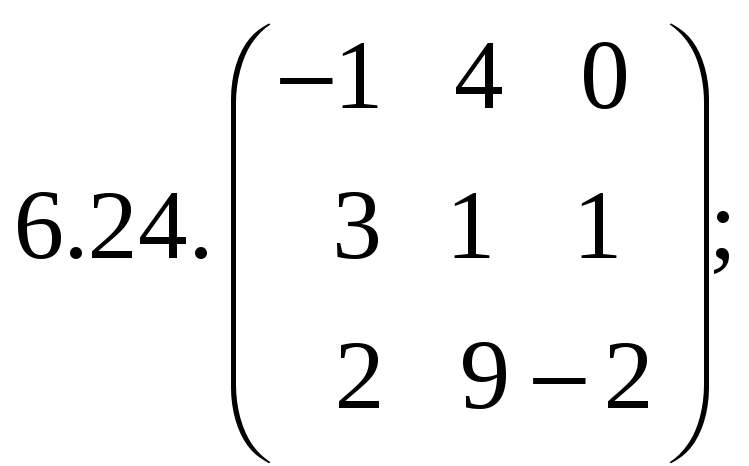
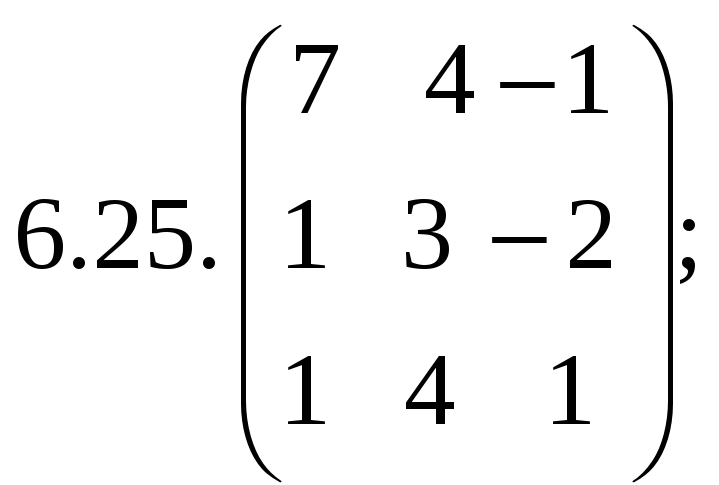
7. Найти матрицу, область значений и ядро линейного оператора А. Определить ранг и дефект:
-
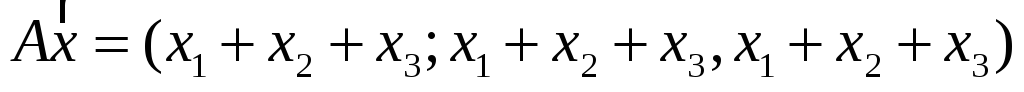 .
. -
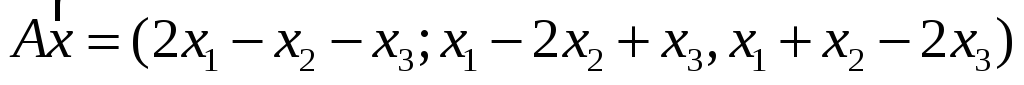
-
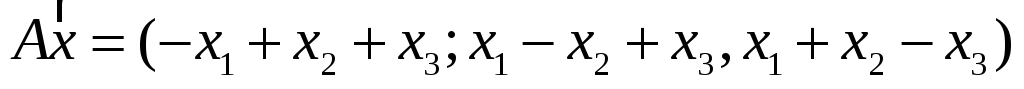
-
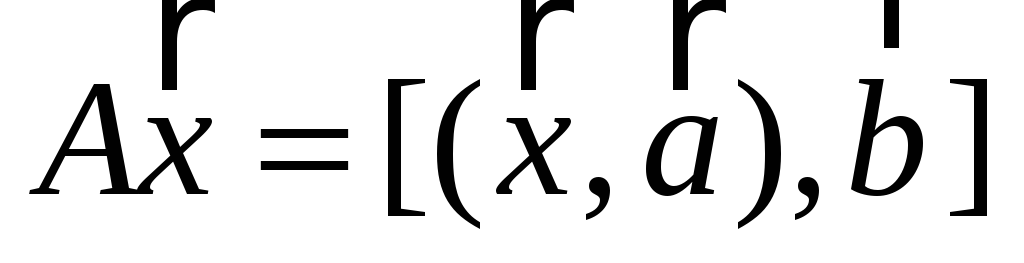 ,
где
,
где
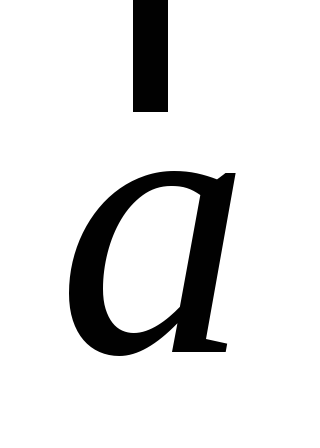 и
и
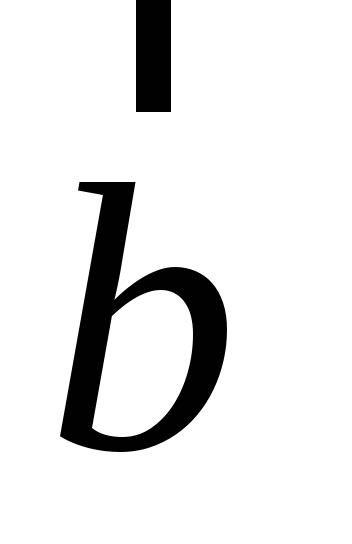 - заданные векторы в
- заданные векторы в
 .
. -
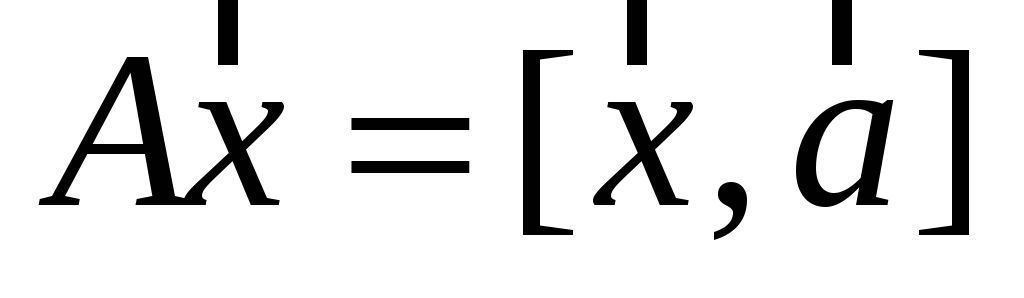 ,
где
,
где
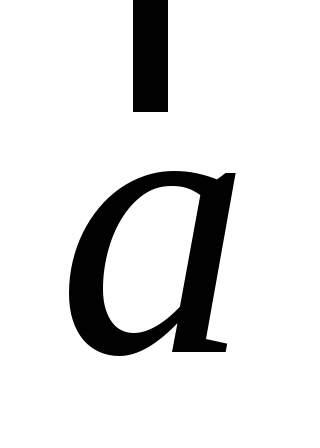 - заданный вектор в
- заданный вектор в
 .
. -
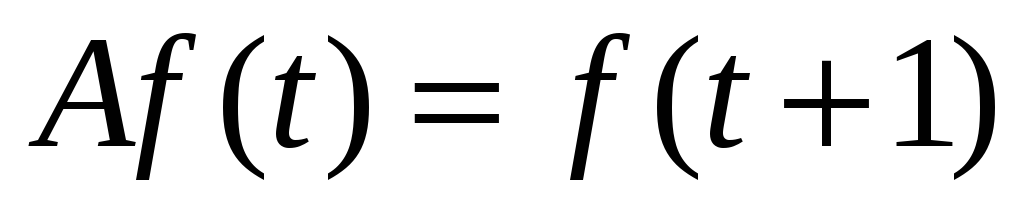 -
многочлены степени
-
многочлены степени
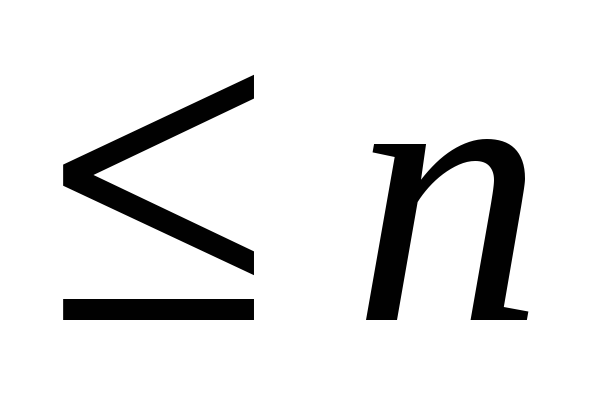 .
. -
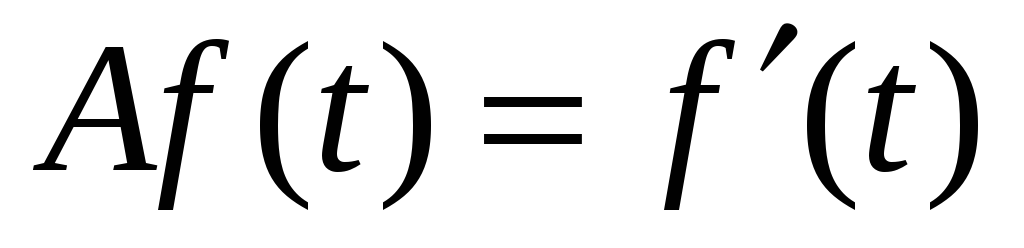 -
многочлены степени
-
многочлены степени
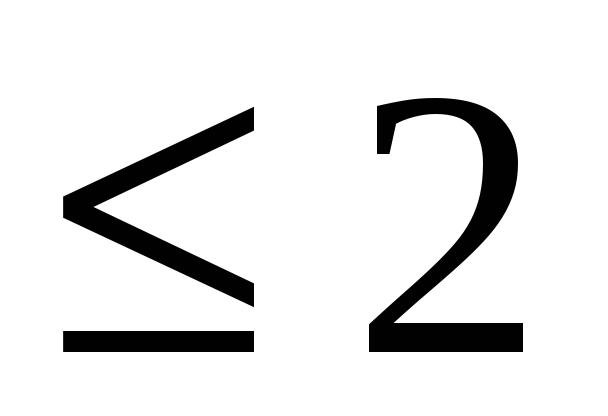 ,
А
- оператор дифференцирования.
,
А
- оператор дифференцирования. -
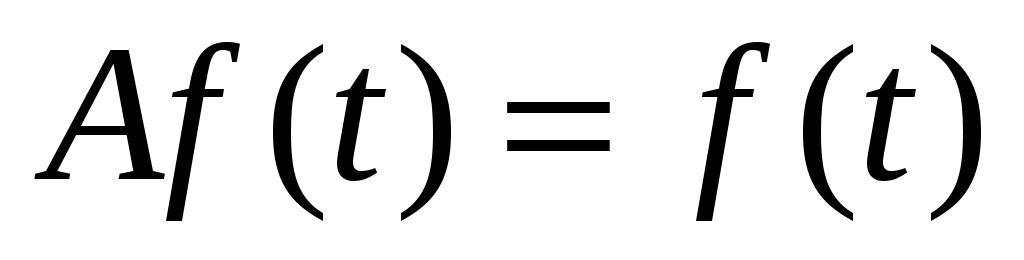 -
многочлены степени
-
многочлены степени
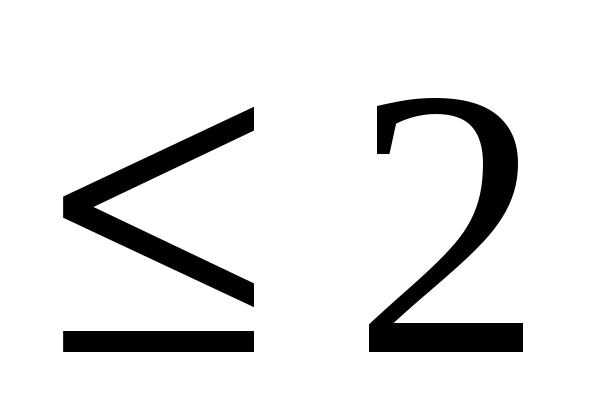 .
.
-
А - зеркальное отражение относительно плоскости
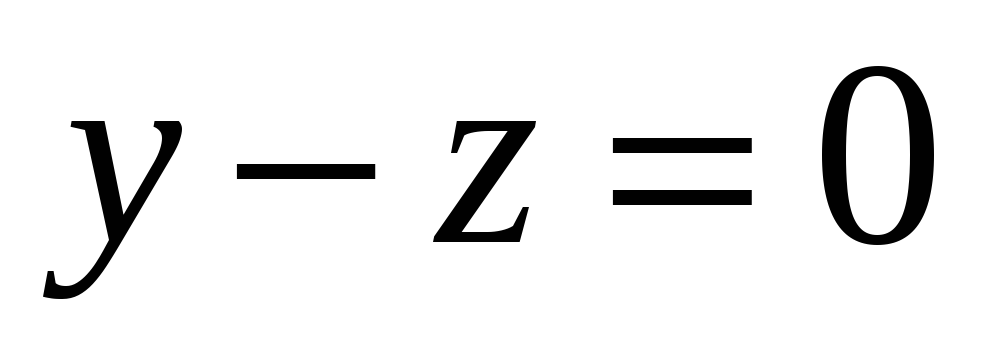 .
. -
А - зеркальное отражение относительно плоскости
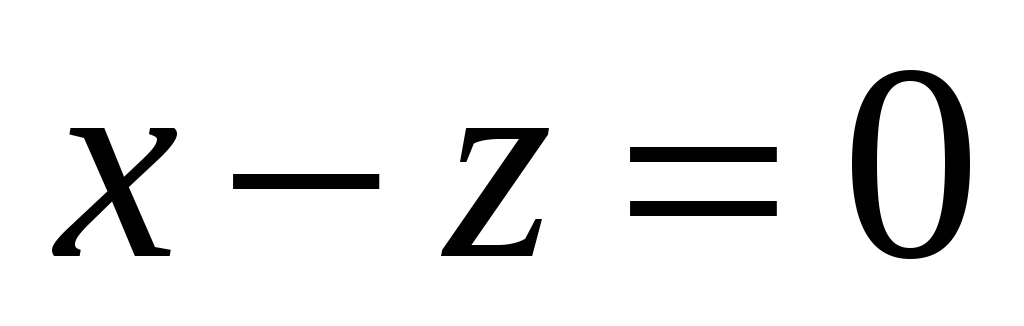 .
. -
А - зеркальное отражение относительно плоскости
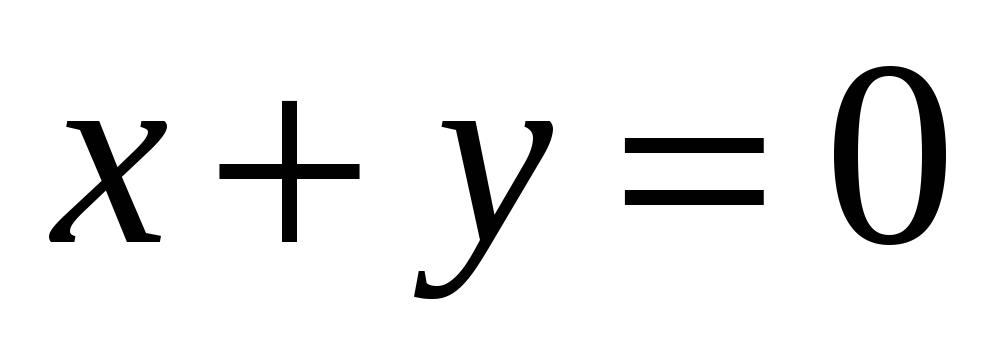 .
. -
А - зеркальное отражение относительно плоскости
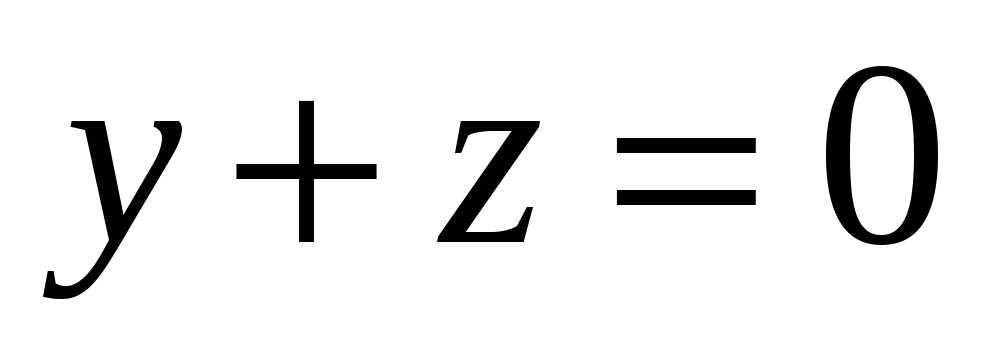 .
. -
А - зеркальное отражение относительно плоскости
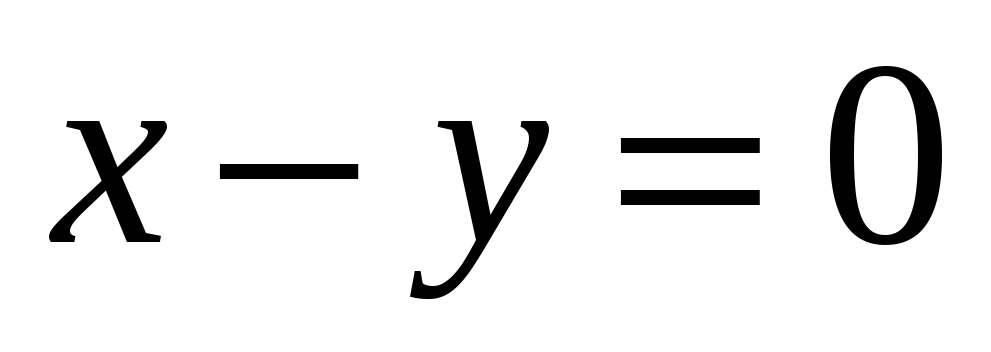
-
А - зеркальное отражение относительно плоскости
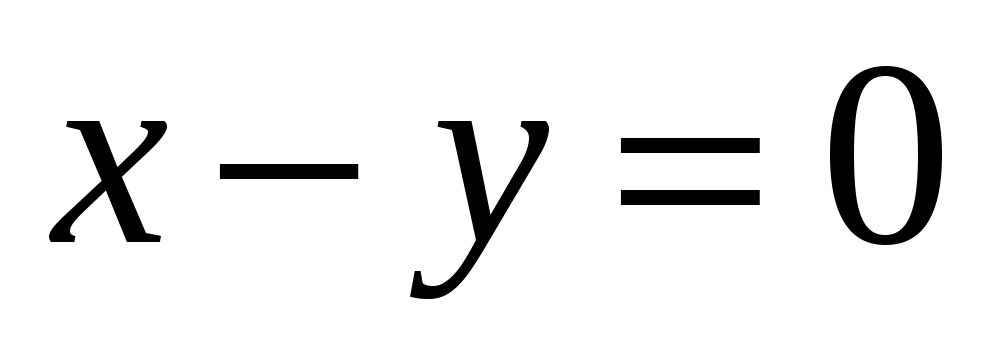 .
. -
А - зеркальное отражение относительно плоскости
 .
. -
А - проектирование на плоскость
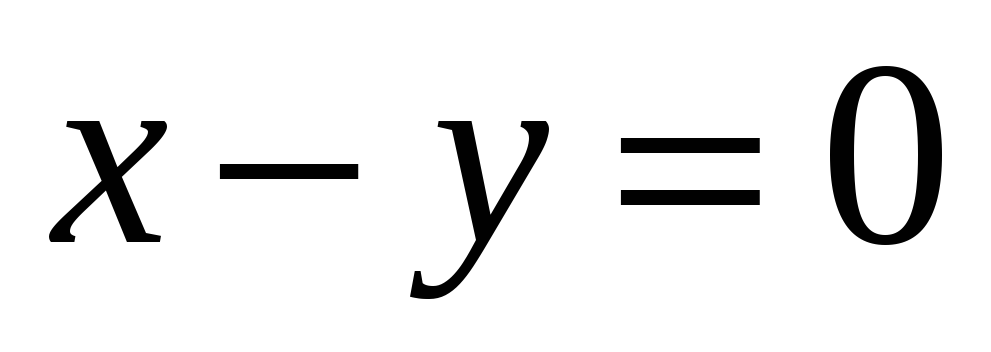 .
. -
А - проектирование на плоскость
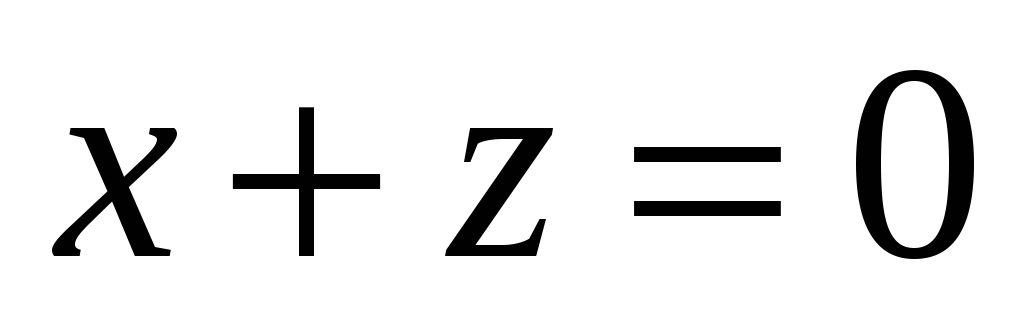 .
. -
А - проектирование на плоскость
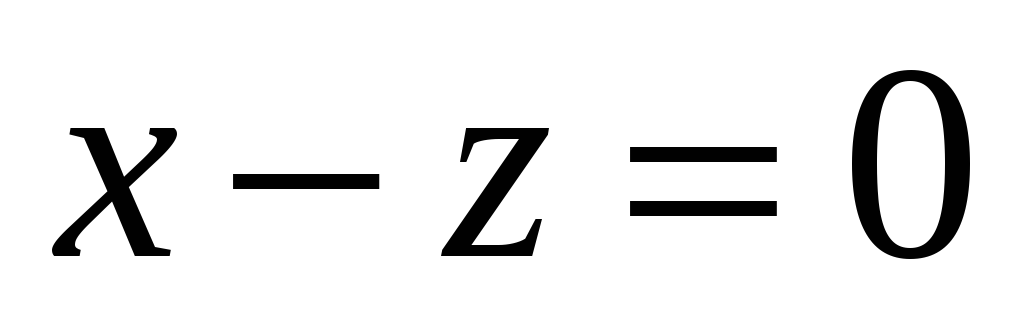 .
.
-
А - проектирование на плоскость
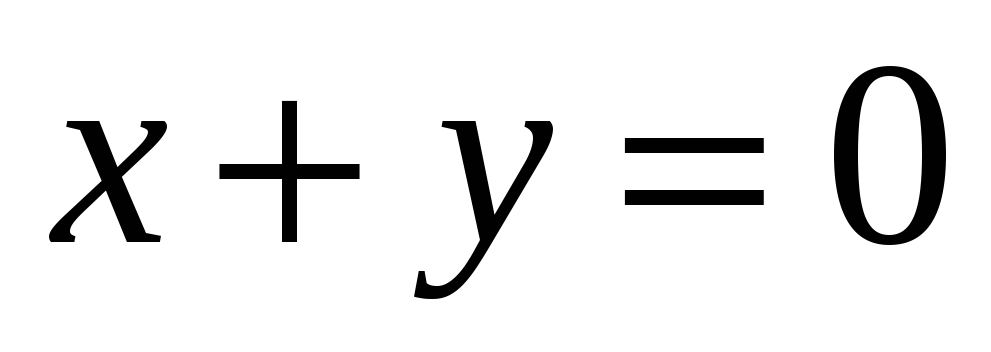 .
. -
А - проектирование на плоскость
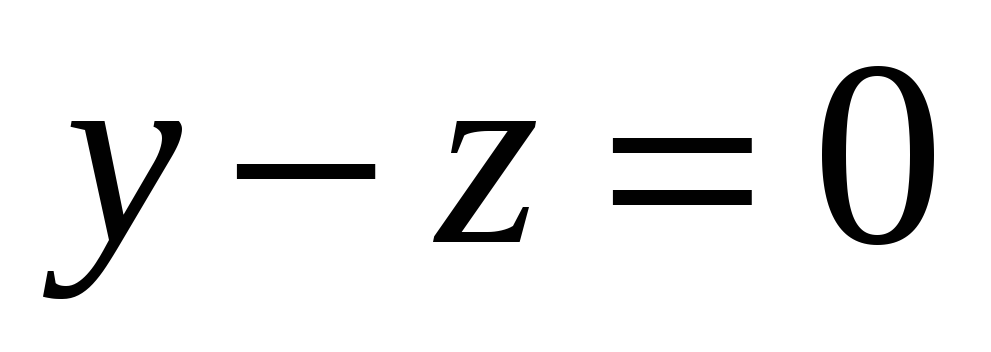 .
. -
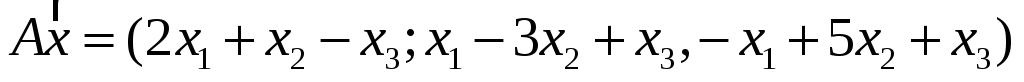
-
А – зеркальное отражение относительно плоскости
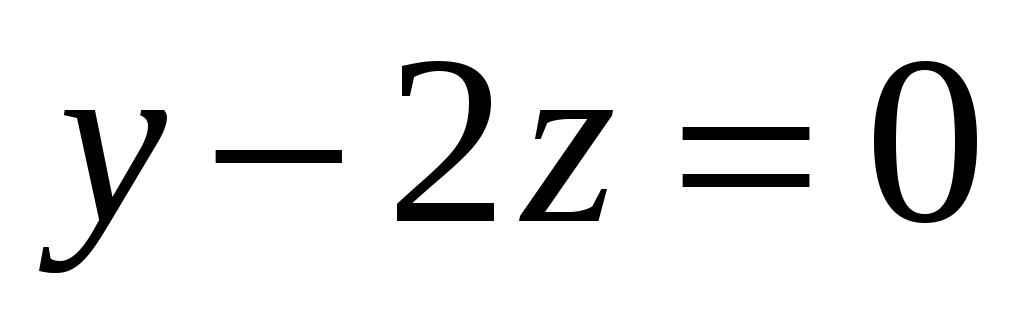
-
А – зеркальное отражение относительно плоскости
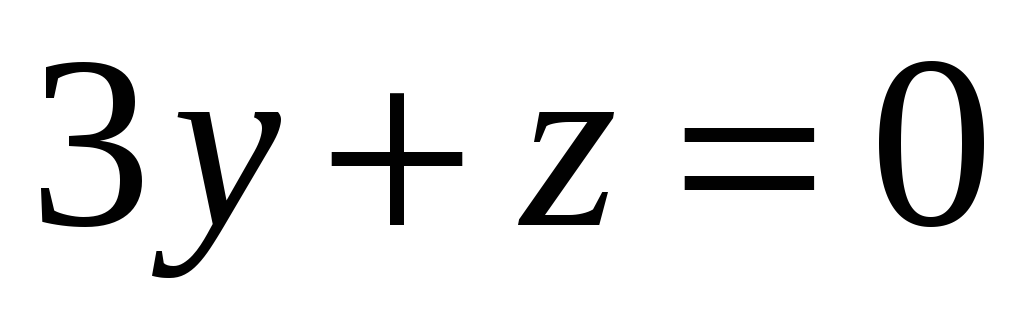
-
А – проектирование на плоскость
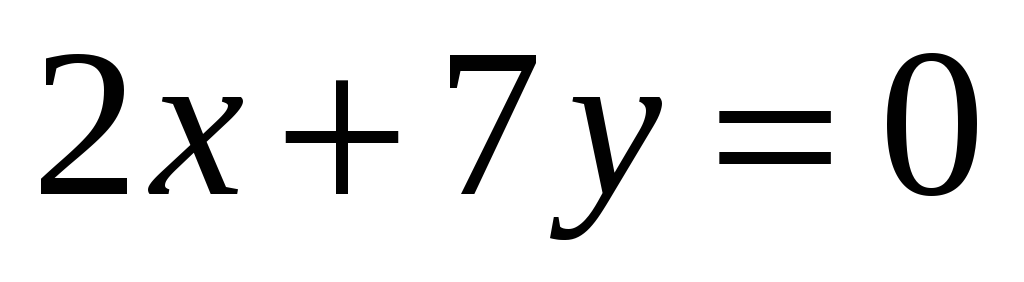
-
А – проектирование на плоскость
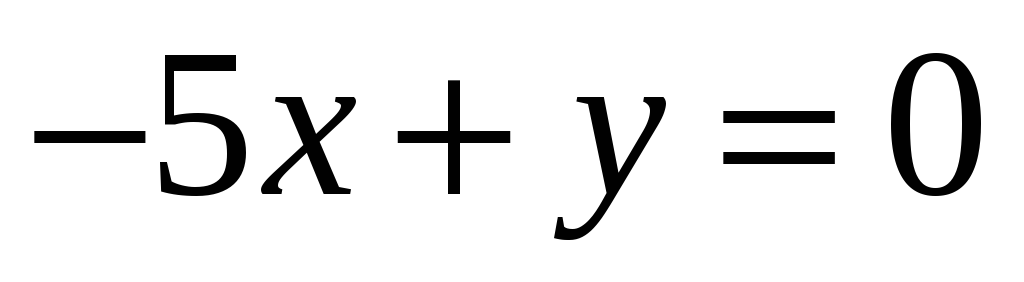
8. Найти собственные векторы линейного оператора. Привести матрицу линейного оператора к нормальному виду (форме Жордана).
8.1.
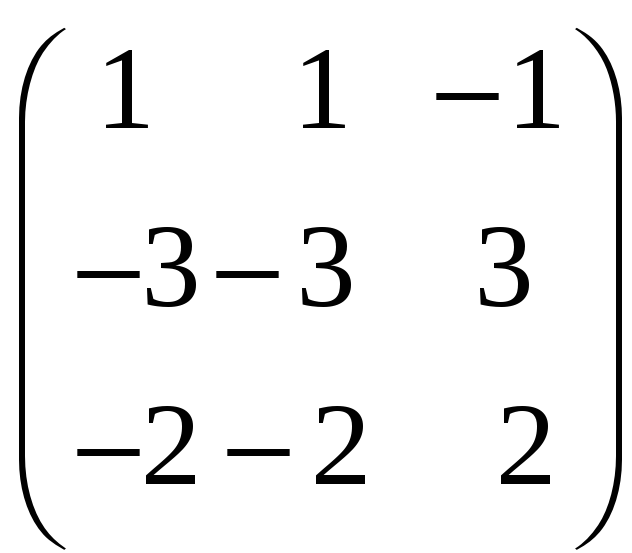 ;
8.2.
;
8.2.
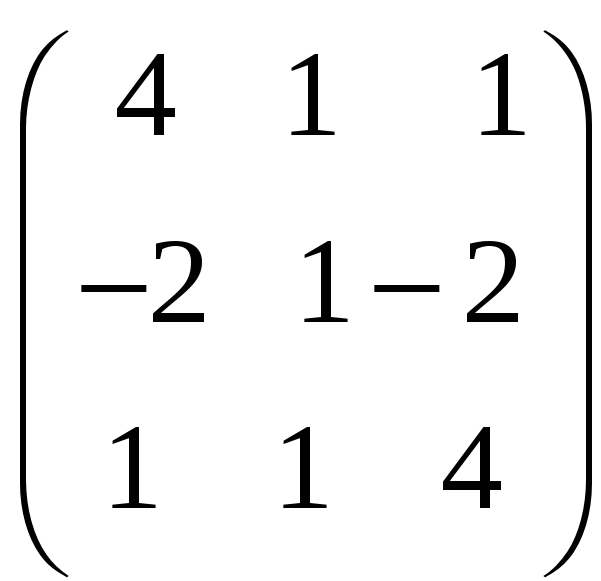 ;
8.3.
;
8.3.
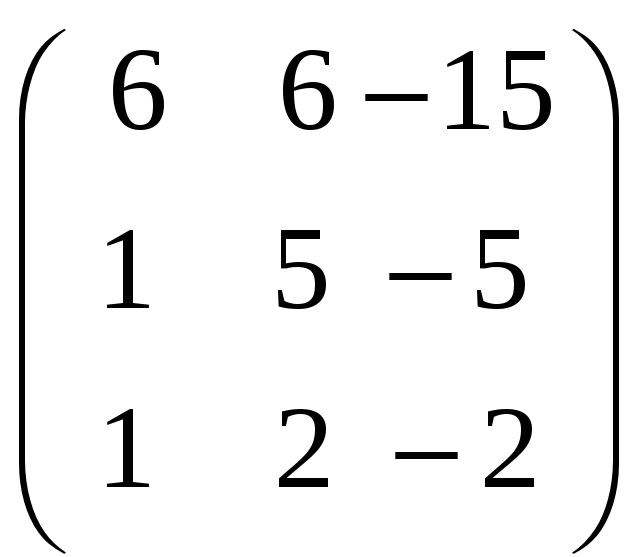 ;
;
8.4.
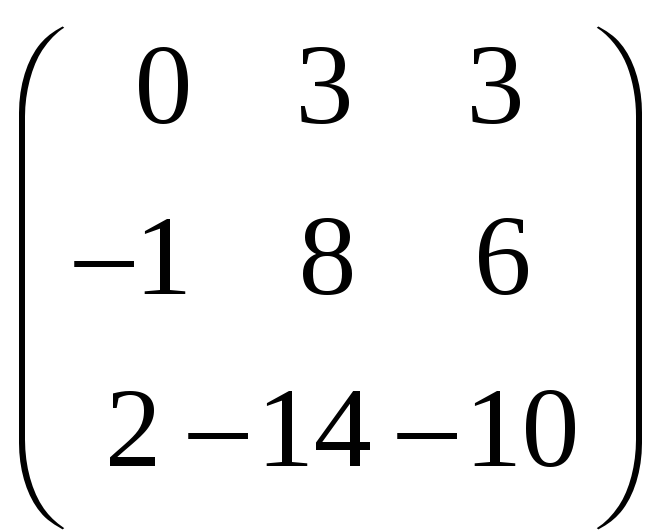 ;
8.5.
;
8.5.
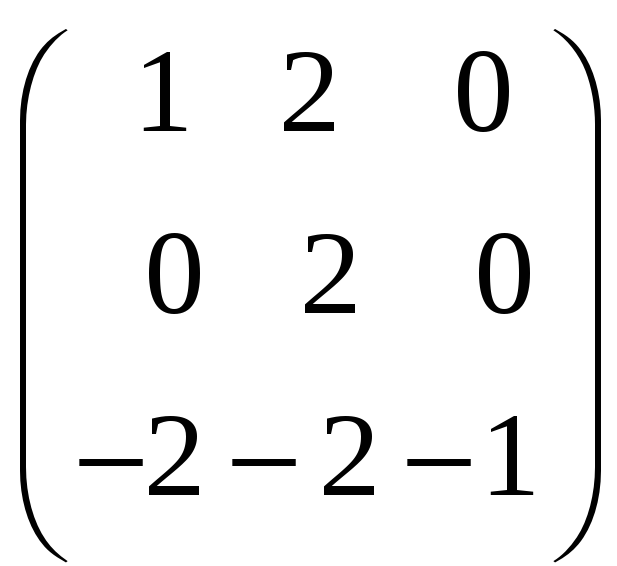 ;
8.6.
;
8.6.
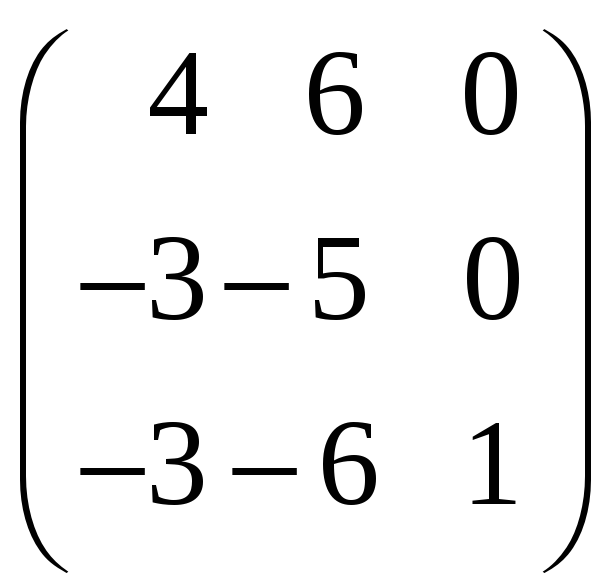 ;
;
8.7.
 ;
8.8.
;
8.8.
 ;
8.9.
;
8.9.
 ;
;
8.10.
 ;
8.11.
;
8.11.
 ;
8.12.
;
8.12.
 ;
;
8.13.
 ;
8.14.
;
8.14.
 ;
8.15.
;
8.15.
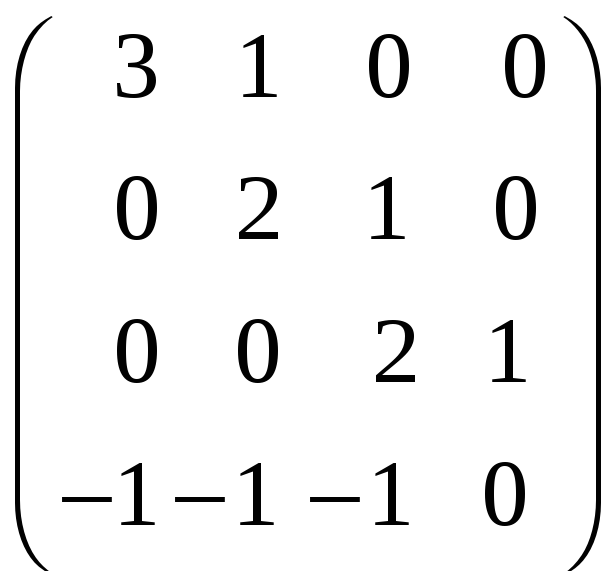 ;
;
8.16.
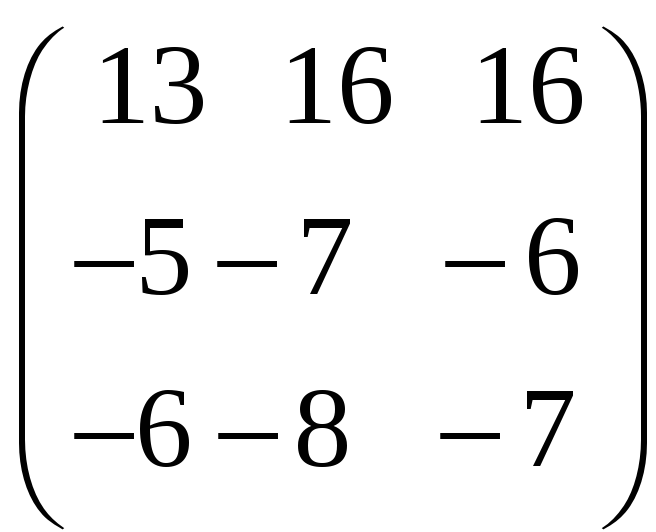 ;
8.17.
;
8.17.
 ;
8.18.
;
8.18.
 ;
;
8.19.
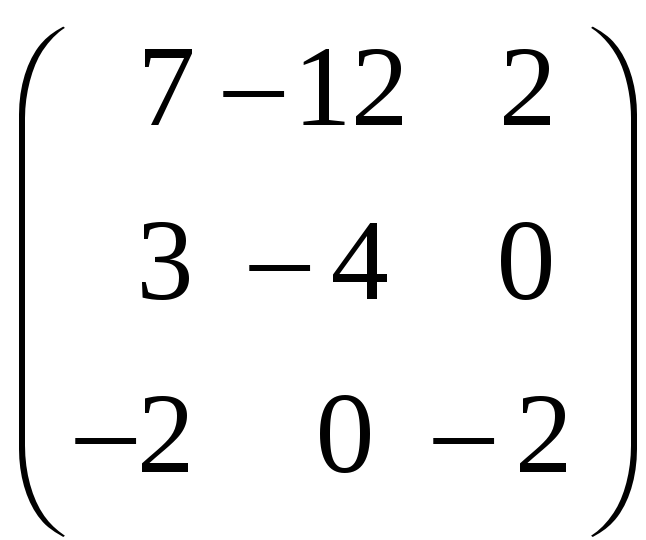 ;
8.20.
;
8.20.
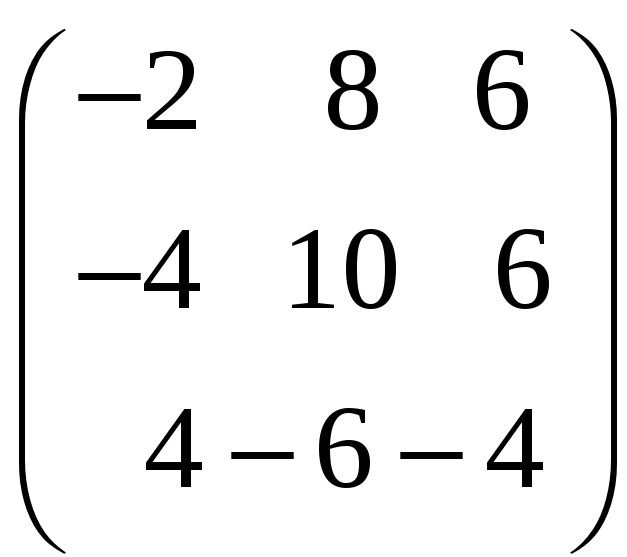 ;
8.21.
;
8.21.
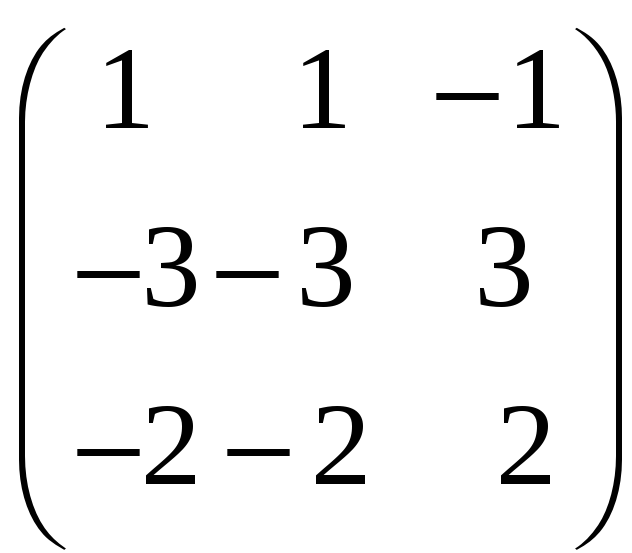 ;
;
8.22.
 ;
8.23.
;
8.23.
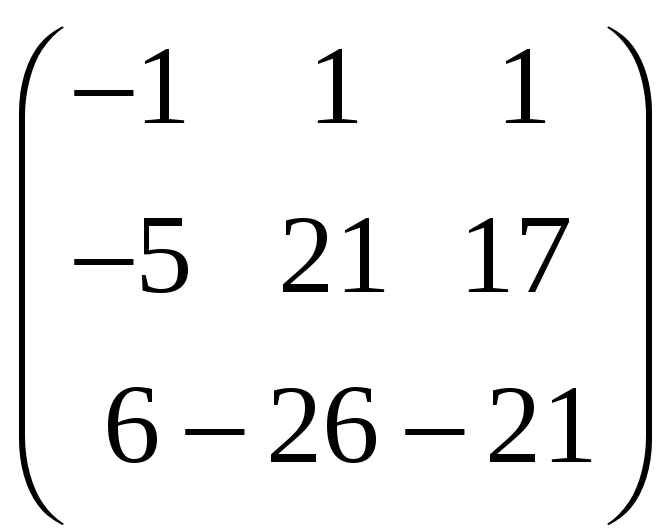 ;
8.24.
;
8.24.
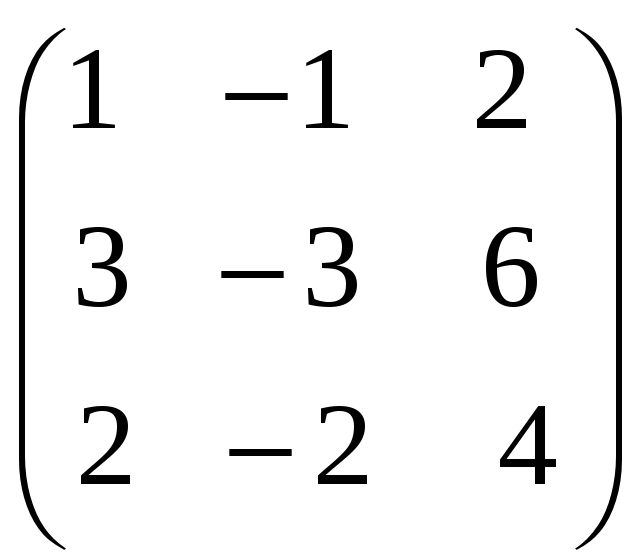 ;
;
8.25.
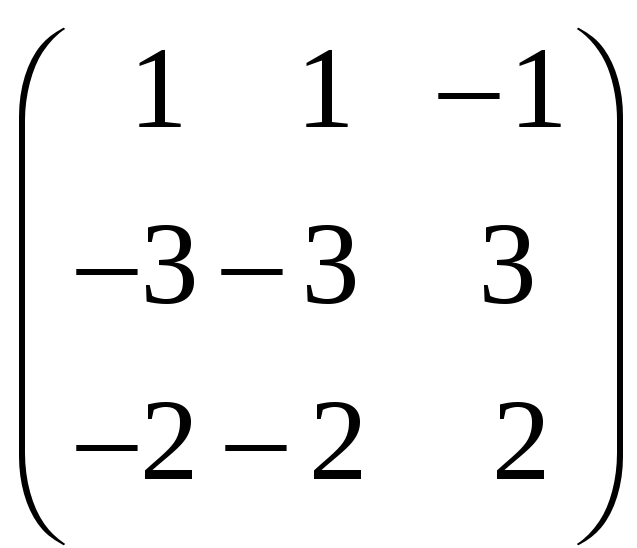 .
.
