5.4 Рекурентні формули для функції Бесселя

Помножимо (5.11) на та продиференціюємо отриманий вираз по , маємо

.

Таким чином

. (5.12)

Аналогічним чином можна одержати

. (5.13)

Продиференціювавши ліві частини рівностей (5.12) та (5.13) отримуємо

, (5.14)

. (5.15)

Звідки

, (5.16)

. (5.17)

Додавши та віднявши рівності (5.16) та (5.17), отримаємо

, (5.18)

. (5.19)

5.5 Інтегральне представлення Пуассона функції Бесселя та його використання

Циліндричні функції допускають прості інтегральні представлення. Одне з найпростіших інтегральних представлень функції Бесселя належить Пуассону.

Розглянемо бета-функцію та її властивість . Зробимо заміну . Тоді

(5.20)

Робимо заміну , тоді

. (5.21)

Звідки

. (5.22)

Підставимо рівність (5.22) у (5.11), маємо

.

Змінимо порядок підсумовування та інтегрування, тоді

. (5.23)

Скористаємося властивістю гамма-функції

,

в якій зробимо заміну . Тоді

або

.

З рівності (5.23) знаходимо

.

Остаточно одержуємо

. (5.24)

Оскільки підінтегральна функція парна, то формулу (5.24) можна переписати так

(5.25)

Застосовуючи у формулі (5.25) заміну , отримуємо

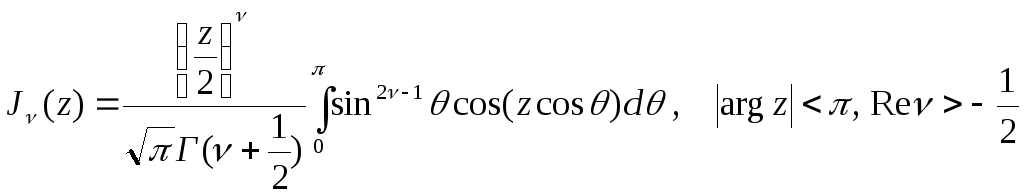(5.26)

Формули (5.25) та (5.26) – інтегральне представлення Пуассона.

Приймемо у (5.24) , тоді

. (5.27)

Із (5.27) випливає, що

Таким чином, для дійсних х .

Тепер зробимо заміну Тоді

. (5.28)

З рівності (5.28) випливає, що функцію Бесселя з додатним половинним індексом можна виразити за допомогою елементарних функцій. За допомогою рекурентних формул можна одержати подібний результат і для функцій з від’ємним половинним індексом. Наприклад,

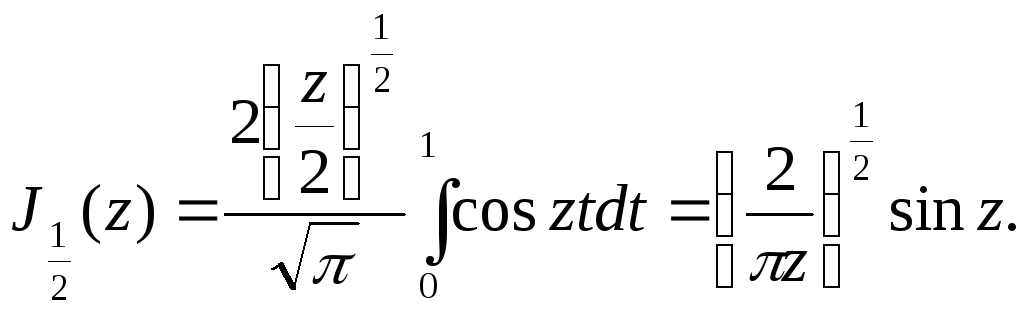
5.6 Сферичні функції. Поліноми Лежандра

Сферичними функціями називаються розв’язки лінійного диференціального рівняння

, (5.29)

де – комплексна змінна, та – параметри, що можуть приймати довільні цілі додатні дійсні чи комплексні значення.

Рівняння (5.29) зустрічається у математичній фізиці при інтегруванні рівняння Лапласа у криволінійних координатах.

Найпростіший клас сферичних функцій складають поліноми Лежандра, які є розв’язками рівняння (5.29) при . Наступний за ступенем складності клас сферичних функцій утворюють сферичні функції Лежандра, які є розв’язком рівняння (5.29) при і довільному дійсному чи комплексному .

Припустимо, що у рівнянні (5.29) , тобто

. (5.30)

Покажемо, що одним із інтегралів рівняння (5.30) є функція

(5.31)

Функції (5.31) називаються поліномами Лежандра.

Позначимо

.

Тоді

,

або

. (5.32)

Продиференціюємо рівність (5.32) (n+1) раз. Отримуємо

. (5.33)

Диференціювання можна виконати за формулою Лейбніца

. (5.34)

Позначимо для першого доданка (5.33) , а для другого доданка . Зрозуміло, що в обох випадках . Маємо

,

або

. (5.35)

Помножимо рівність (6.35) на , маємо

,

або

. (5.36)

Рівність (5.36) означає, що поліноми Лежандра є розв’язками рівняння (5.30).

Знайдемо інший розв’язок рівняння (5.30), який був би лінійно незалежним з розв’язком .

Нехай та – розв’язки рівняння (5.30), тоді

,

.

Помножимо перше рівняння на , а друге – на та віднімемо отримані рівняння, маємо

. (5.37)

Проінтегруємо тотожність (5.37)

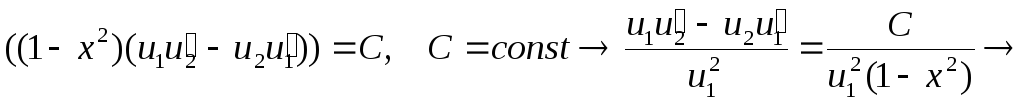
. (5.38)

Таким чином, якщо та – розв’язки рівняння (5.30), то вони пов’язані співвідношенням (5.38), у якому та можуть бути довільними. Якщо , то та лінійно незалежні. Візьмемо в якості поліноми Лежандра: . Тоді, згідно з (5.38), маємо

. (5.39)

У рівності (5.39) – лінійно незалежна функція з . Функція називається функцією Лежандра другого роду ().

Нехай , тоді

(5.40)

Візьмемо , тоді

. (5.41)

Нехай , тоді

. (5.42)

Загалом

, (5.43)

де – поліном степеня .

Оскільки функції та лінійно незалежні, то загальний розв’язок рівняння (5.30) може бути записаний у вигляді

(5.44)

де та – довільні константи.