2.1.3. Расчет ускорений

Расчет ускорений проводится для двух положений рабочего хода механизма, в которых сила полезного сопротивления не равна нулю. Ускорения определяются подобно скоростям, расчет которых был проделан выше (п. 2.1.2). В данном курсовом проекте рассчитываются линейные и угловые ускорения в положениях механизма №2 и №4.

Первоначально определим ускорение точки А кривошипа. Оно является постоянным и равно произведению квадрата угловой скорости кривошипа на его длину:

. (2.4)

м/с².

Нахождение ускорений будем производить методом планов, для этого запишем векторное уравнение ускорения точки В:

(2.5)

где и - нормальная и тангенциальная составляющие ускорения звена АВ соответственно.

Решим уравнение (2.10) графически. Для этого примем масштабный коэффициент плана ускорений , равный:

,

где мм.

.

.

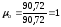
Строим план ускорений согласно направлению векторов:

- направлено из точки А в точку О₁;

- направлено из точки В в точку А;

- направлено перпендикулярно звену АВ;

- направление задается направляющей t – t.

Определим нормальную составляющую ускорения звена АВ:

, (2.6)

м/с².

Для построения плана ускорений:

• выбираем полюс р_а ;

• строим вектор ускорения точки А;

• из конца вектора строим луч параллельный звену АВ, и на этом луче откладываем отрезок an равный: ;

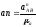• через точку n проводим прямую перпендикулярную АВ, отмечаем точку пересечения ее с направляющей t-t – точка b;

• отрезок р_аb – ускорение точки В на плане ускорений.

Ускорения центров масс определяем по принципу подобия:

,

,

.

План ускорений для положения №2 представлен на рис. 2.1.4

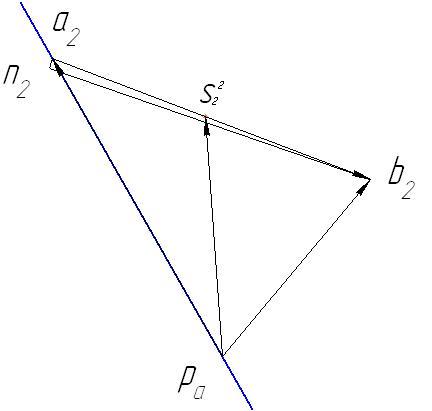
Рис. 2.1.4 План ускорений для положения №2

Численные значения ускорений вычислим по формулам:

м/с²,

м/с²,

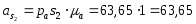м/с²,

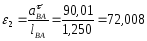м/с²,

1/с².

Полученные значения всех ускорений для положений механизма №8 и №10 приведены в таблице 3.

Таблица 3

	aa	ab	aAB	as2	ε2
№8	90.72	61.16	90.05	63.65	72.008
№10		41.04	72.8	61.4	57.82

2.2 Кинематический анализ методом диаграмм

Метод кинематических диаграмм позволяет наглядно просмотреть, как изменяются перемещение, скорость и ускорение за цикл работы механизма.

Примем масштабный коэффициент равный .

Для построения диаграмм нам потребуется масштабный коэффициент времени и масштабный коэффициент угла поворота . Эти коэффициенты рассчитаем по формулам:

,

где t_ц – время цикла, , ; L=180 мм.

сек/мм.

град/мм.

Диаграмма перемещений представлена на рис. 2.2.1

Рис 2.2.1. Диаграмма перемещения

Переносим скорости выходного звене на диаграмму скоростей с учетом полученных масштабных коэффициентов. Полученные значения скоростей соединяем линией, и в результате имеем диаграмму для скорости выходного звена в двенадцати положениях механизма (рис. 2.2.2).

Диаграмма скорости строится на первом листе графической части.

Рис. 2.2.2. Диаграмма скорости

Диаграмма ускорений строится методом графического дифференцирования. Для этого:

• диаграмму скоростей аппроксимируем ломаной линией;

• с диаграммы скоростей ось абсцисс переносим на диаграмму ускорений и продолжаем её за начало координат (влево);

• откладываем отрезок Н = 20 мм;

• на диаграмме скоростей определяем точку 1 ^/, затем соединяем её с точкой О прямой линией:

• из точки Р проводим луч, параллельный хорде О1^/. Получаем точку 1^//;

• отрезок О1^// изображает среднее ускорение на временном интервале (0;1);

• чтобы найти точку диаграммы ускорений необходимо из середины временного интервала (0;1) восстановить перпендикуляр и на этот перпендикуляр спроецировать точку 1­^//;

• эти построения повторяем для всего временного интервала.

Определим масштабный коэффициент диаграммы ускорений:

;

.

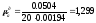
Рис. 2.2.3. Диаграмма ускорений