1.4.4. Уравнение поверхности и уравнение линии в пространстве.

 

Пусть нам заданы декартова прямоугольная система координат Oxyz и некоторая поверхность S.

Определение 1. Уравнение

 

называется уравнением поверхности S (относительно заданной системы координат), если этому уравнению удовлетворяют координаты x, y, z любой точки, лежащей на поверхности S, и не удовлетворяют координаты x, y, z ни одной точки, не лежащей на поверхности S.

 

Пример. Уравнение сферы радиуса R>0 с центром в точке в декартовой прямоугольной системе координат Oxyz имеет вид

 

.

Действительно, точка лежит на указанной сфере тогда и только тогда, когда квадрат расстояния между точками

.

 

Определение 2. Линия в пространстве есть геометрическое место точек, лежащих одновременно на двух поверхностях.

Таким образом, линия в пространстве рассматривается как линия пересечения двух поверхностей.

 

Если - уравнения двух поверхностей, пересечением которых является данная линия L, то два уравнения

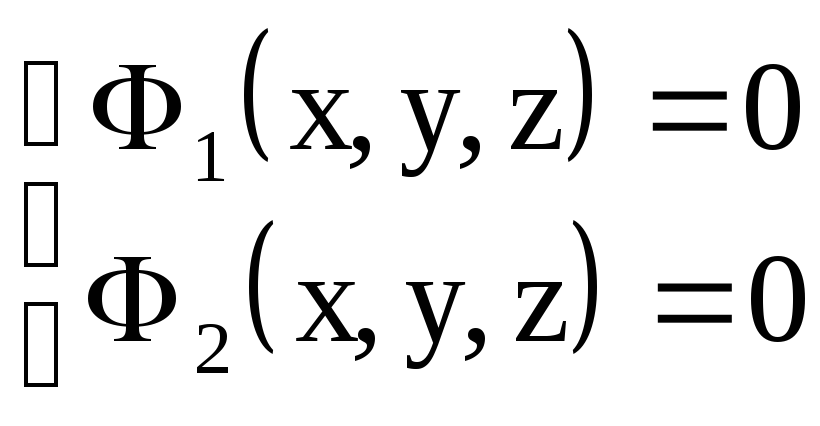
совместно определяют линию L.

 

Как и в случае плоской линии (п.2) можно линию в пространстве представить параметрически, задав координаты x, y, z любой точки данной линии как непрерывные функции некоторого параметра t :

 

,

 

определенные в некотором промежутке изменения параметра .

 

Для отыскания точек пересечения поверхностей и линий следует решить совместно уравнения, определяющие указанные линии и поверхности.

 

1.5. Различные виды уравнений прямой на плоскости.

 

1.5.1. Общее уравнение прямой.

 

Уравнение

Ax+By+C=0 (6.1)

 

с произвольными коэффициентами A, B и C такими, что A и B не равны одновременно нулю, называется общим уравнением прямой L.

 

Уравнение (6.1) имеет хотя бы одно решение , т.е. существует точка , координаты которой удовлетворяют уравнению (6.1):

 

. (6.2)

 

Вычитая из уравнения (6.1) тождество (6.2), получаем уравнение

 

, (6.3)

 

эквивалентное уравнению (6.1).

 

Если точка лежит на прямой L, то ее координаты удовлетворяют уравнению (6.3), векторы , перпендикулярный к прямой L, и перпендикулярны и их скалярное произведение

 

равно нулю. Если же точка не лежит на прямой L , то ее координаты не удовлетворяют уравнению (6.3).

 

Итак, уравнение (6.3) определяет прямую L, проходящую через точку и перпендикулярную вектору . Этот вектор будем называть нормальным вектором прямой (6.1).

 

Замечание. Если два уравнения определяют одну и ту же прямую, то существует такое вещественное число t, что справедливы равенства .

 

1.5.2. Уравнение прямой с угловым коэффициентом.

 

Пусть прямая не параллельна оси Ox, тогда в уравнении (6.1) коэффициент . Углом наклона этой прямой к оси Ox назовем угол , образованный прямой с положительным направлением оси Ox.

 

Если прямая параллельна оси Ox, то угол наклона  будем считать равным нулю.

 

Угловым коэффициентом прямой назовем тангенс угла наклона этой прямой к оси Ox, .

Для прямой, параллельной оси Ox, угловой коэффициент равен 0, а для прямой, перпендикулярной оси Ox, угловой коэффициент не существует .

 

Из уравнения (6.3) и того, что - нормальный вектор прямой, следует, что .

 

Отсюда получим уравнение прямой с угловым коэффициентом в виде . Если обозначить , то последнее уравнение примет вид

 

. (6.4)

 

Это уравнение и называется уравнением прямой с угловым коэффициентом. Здесь k- угловой коэффициент данной прямой, а b - отрезок, отсекаемый данной прямой на оси Oy, начиная от начала координат (при ).