4.3. Понятие функции. Предел функции. Непрерывность.

 

4.3.1. Определение функции. Определение 1.

 

 

 

Пусть даны два непустых подмножества {x}и {y}множества R.

 

Если каждому элементу x из {x} ставится в соответствие один элемент y из {y}, то y называется функцией f (отображением) аргумента x. Это записывается в виде:

 

.

 

Другими словами, с помощью функции y=f(x) подмножество {x} отображается в подмножестве {y}, поэтому допустима запись

 

Подмножество {x} или D(f) называется областью определения функции y, подмножество {y} или E(f) - множеством ее значений. Аргумент x часто называют независимой переменной, функцию y -зависимой переменной, а соответствие между ними- функциональной зависимостью.

 

Частным значением функции y=f(x) при x=a, a{x} называется то значение y , которое соответствует заданному значению x. Оно обозначается через f(a), или y_x=a .

 

Функции могут быть заданы аналитически, графически и с помощью таблиц.

 

 

4.3.2. Способы задания функций.

 

Функция задана аналитически , если функциональная зависимость выражена в виде формулы, которая указывает совокупность тех математических операций, которые должны быть выполнены, чтобы по данному значению аргумента найти соответствующее значение функции.

 

Пример 1. Функция Дирихле

 

.

 

Пример 2. (рис.1)

Рис.1

 

Определение 2. Графиком функции y=f(x), xx называется геометрическое место точек на плоскости с координатами (x,f(x)), где xx.

 

Графический способ задания функции, помимо геометрического изображения функции, заданной уравнением, удобен тогда, когда функцию трудно задать аналитически. Задать функцию графически - это значит задать ее график.

 

При табличном способе задания функции рядом с числовым значением аргумента выписывается соответствующее значение функции. Недостатком табличного способа задания функции является то, что в таблице могут быть указаны не все, а лишь отдельные значения аргумента и функции. Особенности изменения функции при этом могут быть искажены.

 

 

4.3.3. Монотонные функции.

Пусть функция y=f(x) определена на множестве {x} и точки

x₁ ,x₂{x}любые точки, связанные соотношением x₁< x₂ .

 

Тогда

 

 

 

4.3.4. Сложная функция.

Функции, полученные в результате суперпозиции (или наложения) двух или нескольких функций, называются сложными.

 

Если функция y зависит от переменной x, т.е. y=f(x), xx; a x, в свою очередь, является какой-либо функцией от независимой переменной t, т.е. x=(t), t{t}, то переменная y называется функцией от функции (или сложной функцией от t) и записывается в виде

y=f(x), x=(t); или y=f((t)).

 

Область определения сложной функции - это множество тех значений t из {t}, для которых соответствующие значения x принадлежат области определения {x} функции y=f(x).

 

 

4.3.5. Обратная функция.

Пусть задана некоторая функция y=f(x), т.е. некоторое соответствие между множествами D(f) и E(f). Предположим, для определенности, что D(f)=[a,b], a E(f)=[]. Пусть далее каждому y[] соответствует одно и только одно значение x[a,b], для которого f(x)=y (рис.2). Тогда на сегменте [] можно определить функцию x=f^-1 (y), ставя в соответствие каждому y из [] то значение x из [a,b], для которого f(x)=y. Функция x=f^-1 (y) называется обратной для функции y=f(x).

 

 

 

Рис.2.

 

Замечание 1. Вместо сегментов [a,b] и [] можно рассматривать интервалы (a,b) и (). Можно допускать, что один или оба интервала (a,b) и () превращаются в бесконечную прямую или в открытую полупрямую.

 

Замечание 2. Если x=f^-1 (y) - обратная функция для y=f(x), то очевидно, функция y=f(x) является обратной для функции x=f^-1 (y). Поэтому функции y=f(x) и x=f^-1 (y) называются взаимно обратными.

 

Одна и та же кривая y=f(x) представляет собой график функции y=f(x) и график обратной функции x=f^-1 (y) (если она существует), но в последнем случае значения аргумента рассматриваются на оси Oy, а значения функции - на оси Ox.

 

Если придерживаться стандартных обозначений и независимую переменную обозначать через x, а функцию через y, то функция, обратная по отношению к y=f(x), запишется в виде y=f^-1 (x). В этом случае график функции y=f^-1 (x) окажется симметричным графику функции y=f(x) относительно прямой x=y - биссектрисы Iи III координатных углов.

 

Для взаимно обратных функций имеют место следующие соотношения: D(f)=E(f^-1), E(f)=D(f^-1), т.е. область определения данной функции совпадает с множеством значений обратной функции и наоборот.

 

 

4.3.6. Допустимые области определения функций.

 

Рассмотрим бесконечное множество {x}R и точку аR.

 

Определение. Точка а называется предельной для множества {x}, если в любой -окрестности т. а имеются точки множества {x}, отличные от а.

 

Замечание 1. Сама точка может принадлежать множеству {x}, а может и не принадлежать этому множеству.

 

Пример 1.

 

 {x}=[0,1], a=0

Пример 2.

 

{x}=(-1,1)\{0}, a=0

рис.3

 

Замечание 2. Множество (а-, а+)\{a}, где >0, называют проколотой -окрестностью т. а. (Обозначение ).

Мы будем рассматривать функции y=f(x), определенные на множестве {x}, для которого точка а является предельной.

 

 

4.3.7. Определение предела функции в точке.

Определение 1. Последовательность {x} называется последовательностью Гейне (для точки а и множества {x}), если x_n x, xa, x_na.

 

Определение 2. (определение предела по Гейне) Число b называется пределом функции y=f(x) в точке , если для любой последовательности Гейне {x_n}соответствующая последовательность значений функций {f(x_n)}сходится к числу b.

 

Таким образом, для доказательства того, что функция y=f(x) не имеет предела в т. а (в смысле определения по Гейне), достаточно указать две последовательности Гейне {x¹_n}и {x¹¹_n}, для которых

 

 

Пример 1. Функция Дирихле y=D(x) не имеет предела в т. =0.

 

Действительно,

 

 

.

 

Пример 2. Функция y=sgnx не имеет предела в т. а=0.

 

 

 

Определение 2. * (определение предела по Коши). Число b называется пределом функции y=f(x) в точке а, или при xa (), если для любого положительного числа  найдется положительное число  такое, что для всех значений аргумента x, удовлетворяющих условию 0<x-a, будет выполняться неравенство f(x)-b .

 

 .

 

Замечание 1. Условия x_n a и 0<x-a в определениях 2 и 2* исключают из рассмотрения т. а. В этой точке функция y=f(x) может быть не определена, либо ее значение может быть отличным от b. Таким образом, предел функции в т. а не зависит от значения функции в этой точке.

 

Замечание 2. Условие 0<x-a< (a- < x < a+)(xa)  x принадлежит проколотой  - окрестности т. а. Условие f(x)-b  b-< f(x)<b+  f(x) принадлежит  - окрестности т. b. Это условие означает, что точки графика функции y=f(x) с координатами (x, f(x)) попадают в  полоску {b-<y<b+} прямой y=b.

 

Рис. 4

 

Замечание 3. В определении 2* достаточно найти = () только для малых >0. Так как из неравенства ₁ < ₂ и f(x)-b₁ , очевидно, следует неравенство f(x)-b₂ для тех же значений x (и, следовательно, для (₂)= (₁)).

 

С другой стороны, если () найдено лишь для достаточно больших , то этого может быть недостаточно для существования предела функции (см. рис.5)

 

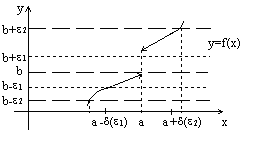
Рис. 5

 

Очевидно, для ₁>0 нельзя найти (₁), для которого при всех x из проколотой (₁) - окрестности т. а график попадал бы в ₁ - полоску y=b. (Для ₂>0 такое (₂) существует).

 

Замечание 4. Если в определении 2* по данному > 0 найдено = ()>0,

то любое ₁ : 0<₁ <() такое можно взять в качестве . Действительно, 0<x-a<₁  0<x-a<() f(x)-b . Отсюда следует, что в определении 2* не нужно искать наибольшее возможное значение  по данному значению > 0.

Замечание 5. Определение 2* можно сформулировать следующим образом:, если для любой  - окрестности точки b , существует такая - окрестность т. а, что для всех значений аргумента x, принадлежащих этой - окрестности и отличных от а, значение функции f(x) попадает в  - окрестность т. b.

 

Замечание 6. В определении предела требуется существование симметричной окрестности (- окрестности) точки а, но для  - окрестности т. b, может существовать несимметричная большая окрестность. (см. рис. 2).

 

Теорема. Определения 2 и 2*предела функции по Гейне и Коши эквивалентны.

Пример 3. Доказать по определению, что .

 

Запишем определение предела по Коши для данной функции.

 

 

Задача состоит в том, чтобы по  найти , при котором справедлива эта импликация.

 

Рассмотрим неравенство x³ +x-10<  и будем искать часть множества его решений вида x-2< h(), тогда h() можно будет взять в качестве .

 

x³ + x-10= x³ - 8+ x-2=(x-2)(x² +2x+4+1)

x³ + x-10< E x-2x² +2x +5.

 

Рассмотрим сегмент [1, 3] , на котором функция x²+2x+5 является ограниченной: x² +2x+5 9+6+5=20, тогда

 

 

Отсюда, в качестве  можно взять Число 1, т.к. x1,3. Таким образом, условие ограниченности x² +2x +5, а следовательно, возможность сведения неравенства x³ +x-10<  к более простому повлекло за собой ограничение области изменения x , т.е. ограничение на величину  сверху. Если  мало (например, <1), то , т.е. ограничение 1 не является существенным. Далее заметим, что даже при малых >0 число не является наибольшим возможным . Однако, как мы уже отмечали, наибольшее  в определении предела и не нужно.