3.5. Уравнение прямой в пространстве.

 

Рассмотрим произвольную прямую, обозначим ее буквой а. Обозначим через П₁ и П₂ какие-нибудь две различные плоскости, пересекающиеся по прямой а и предположим, что уравнения этих плоскостей будут: А₁x+В₁y+С₁z+D₁=0 и А₂x+В₂y+С₂z+D₂=0. Так как прямая а представляет собой пересечение плоскостей П₁ и П₂, то она определяется совместным заданием двух уравнений:

 

(1)

 

Поставим задачу: всегда ли два уравнения первой степени совместно определяют некоторую прямую? Очевидно, это будет только в том случае, когда соответствующие им плоскости не параллельны и не совпадают друг с другом, т.е. когда нормальные векторы этих плоскостей ={А₁, В₁, С₁} и ={А₂, В₂, С₂}не коллинеарны. Два уравнения вида (1) совместно определяют прямую в томи только в том случае, когда коэффициенты А₁, В₁, С₁ одного из них не пропорциональны коэффициентам А₂, В₂, С₂ другого.

 

 

3.6. Направляющий вектор прямой. Канонические уравнения прямой. Параметрические уравнения прямой.

 

Рассмотрим произвольную прямую. Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором этой прямой. Указанные векторы называются направляющими именно потому, что любой из них, будучи задан, определяет направление прямой.

 

 

Направляющий вектор прямой будем обозначать буквой , его координаты - m, n, p:

 

={m; n; p}.

 

Выведем уравнение прямой, проходящей через заданную точку М₀(x₀;y₀; z₀) и имеющей данный направляющий вектор ={m; n; p}.

 

Пусть М(x;y; z) - произвольная ("текущая") точка прямой (рис.2). Вектор ={x- x₀; y- y₀; z- z₀} коллинеарен направляющему вектору ={m; n; p}. Следовательно, координаты вектора пропорциональны координатам вектора :

 

. (1)

 

Этим соотношениям удовлетворяют координаты каждой точки М(x;y; z), лежащей на рассматриваемой прямой, напротив, если точка М(x;y; z) не лежит на прямой, то ее координаты не удовлетворяют соотношениям (1), так как в этом случае векторы и не коллинеарны и координаты их не пропорциональны. Таким образом, уравнения (1) представляют собой уравнения прямой, проходящей, через точку М₀(x₀;y₀; z₀) в направлении вектора ={m; n; p}.

 

Уравнения (1) прямой мы будем называть каноническими. Пусть некоторая прямая задана двумя общими уравнениями:

 

(2)

 

Покажем, как составить канонические уравнения этой прямой. Обозначим плоскости, определяемые данными уравнениями, через П₁ и П₂, нормальные векторы этих плоскостей через и . Для составления канонических уравнений данной прямой, нужно:

 

1.  найти произвольную ее точку М₀(x₀;y₀; z₀); для этого следует задать численное значение одной из неизвестных координат x₀,y₀, z₀ и подставить его вместо соответствующей переменной в уравнения (2); после этого две остальные координаты определяются из уравнений (2) путем их совместного решения;

2. найти направляющий вектор ={m; n; p}. Так как данная прямая определена пересечением плоскостей П₁ и П₂, то она перпендикулярна к каждому из векторов и . Поэтому в качестве вектора можно взять любой вектор, перпендикулярный к векторам и , например, их векторное произведение: 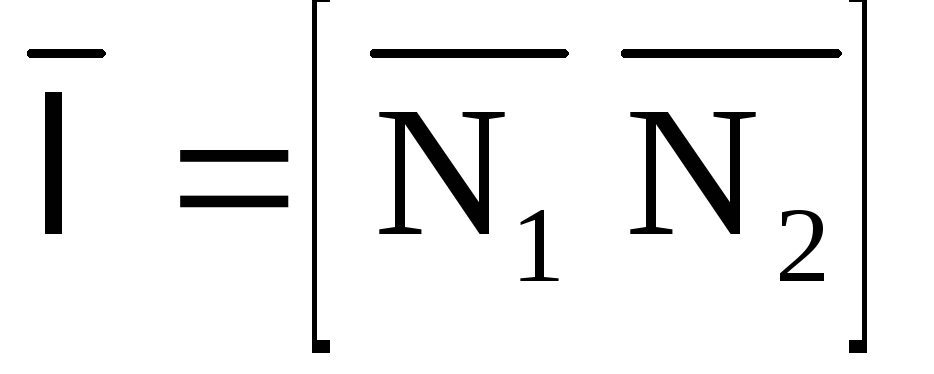. Поскольку координаты векторов и известны: ={А₁; В₁; С₁}, ={А₂; В₂; С₂}, для вычисления координат вектора ={m; n; p} достаточно применить формулу для нахождения координат векторного произведения.

Пример. Найти канонические уравнения прямой

 

Решение. Полагая, например, х₀=1, находим из данной системы: y₀=6, z₀=4; таким образом, мы уже знаем одну точку прямой: М₀(1; 6; 4). Теперь найдем направляющий вектор. Имеем: ={2;1;-1}, ={3;-1;2}; отсюда ={1; -7; -5}, т.е. m=1, n=-7, p=-5. Каноническое уравнение данной прямой мы получим, подставляя найденные значения x₀,y₀, z₀, m, n, p в равенства (1):

 

.

 

Пусть даны канонические уравнения какой-нибудь прямой. Обозначим буквой t каждое из парных отношений, которые участвуют в этих канонических уравнениях; мы получим:

 

.

 

Отсюда

 

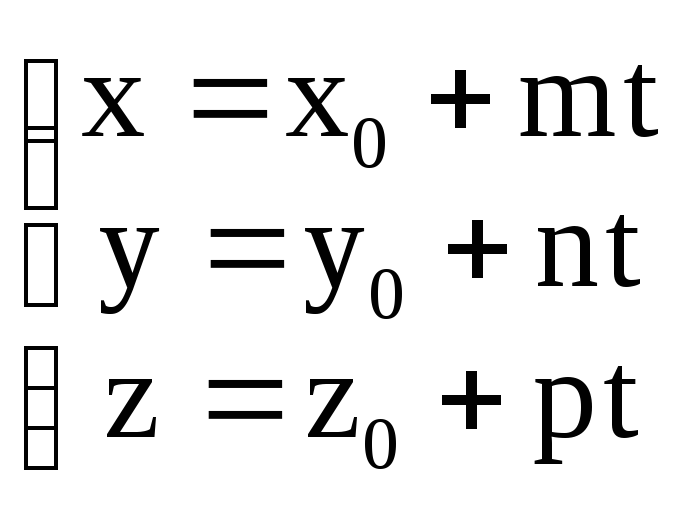(3)

 

Это - параметрические уравнения прямой, проходящей через точку М₀(x₀;y₀; z₀) в направлении вектора ={m; n; p}. В уравнениях (3) t рассматривается как произвольно изменяющийся параметр, x, y, z- как функции от t; при изменении t величины x, y, zменяются так, что точка М(x;y; z) движется по данной прямой. Параметрические уравнения прямой удобно применять в тех случаях, когда требуется найти точку пересечения прямой с плоскостью.

 

Пример. Даны прямая и плоскость x+2y+z-6=0. Найти точку их пересечения.

 

Решение. Задача сводится к определению координат точки x, y, zиз трех данных уравнений (мы имеем два уравнения прямой и одно уравнение плоскости). Полагая , отсюда x=2+t, y=3+2t, z=4+t. Подставляя эти выражения в левую часть уравнения данной плоскости получим (2+t)+2(3+2t)+(4+t)-6=0.

 

Решая это уравнение, находим: t=-1, следовательно, координаты искомой точки будут x=1, y=1, z=3.