Общие сведения

 

Цель изучения – познакомиться с основными понятиями векторной алгебры и применением аппарата векторной алгебры для решения геометрических задач.

Изучив данную тему, студент должен:

Знать: определения основных понятий, свойства всех операций с векторами, выражение всех операций с векторами в координатной форме, условия необходимые и достаточные для: коллинеарности двух векторов перпендикулярности (ортогональности) двух векторов компланарности трех векторов.

Уметь: решать задачи, связанные с линейными и нелинейными операциями с векторами, приобрести навыки применения аппарата векторной алгебры для решения геометрических задач.

Краткое содержание

 

    Данная тема включает в себя :

• понятия свободный вектор, равенство, коллинеарность, компланарность векторов,

• линейные операции с векторами (сумма векторов, произведение вектора на скаляр, разность векторов),

• базис в пространстве, координаты вектора в базисе, ортонормированный базис, декартова прямоугольная система координат, координаты точки),

• нелинейные операции с векторами (скалярное, векторное смешанное произведения).

Практикум

 

             Решить задачи № 372 – 449 из «Сборника задач по Высшей математике» Минорского В.П.

Тема 1. Векторная алгебра.

1.1. Понятие вектора и линейные операции над векторами.

 

1.1.1. Понятие вектора.

 

Геометрическим вектором, или просто вектором, будем называть направленный отрезок.

 

Обозначать вектор будем либо как направленный отрезок символом , где точки A и B обозначают соответственно начало и конец данного вектора, либо символом .

 

 

Начало вектора называют точкой его приложения. Длину вектора будем обозначать символом модуля: или .

 

Вектор называется нулевым, если совпадают его начало и конец. Нулевой вектор имеет длину, равную нулю.

 

Векторы называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.

 

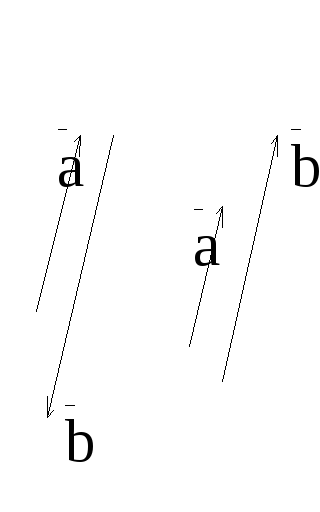
Два вектора называются равными, если они коллинарны, имеют одинаковую длину и одинаковое направление. Все нулевые векторы считаются равными.

 

Точка приложения вектора может быть выбрана произвольно, поэтому изучаемые векторы называют свободными.

 

 

1.1.2. Линейные операции над векторами.

 

Линейными операциями называют операцию сложения векторов и операцию умножения векторов на вещественные числа.

 

Определение 1. Суммой двух векторов и называется вектор, идущий из начала вектора в конец вектора при условии, что вектор приложен к концу вектора .

 

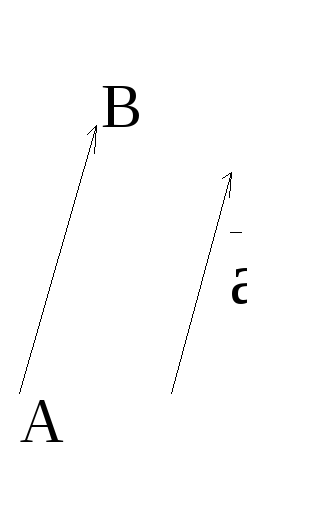
Это правило называют “правилом треугольника”.

 

Свойства сложения векторов:

 

1. 

 

Доказательство. Приложим два произвольных вектора и к общему

 

началу 0. Обозначим через A и B концы векторов и соответственно и рассмотрим параллелограмм OBCA. , .

 

Из определения 1 и OAC следует, что , а из OBC видим, что , ч.т.д.

 

Замечание. При доказательстве свойства 1 нами получено правило сложения векторов, называемое “правилом параллелограмма”: если векторы и приложены к общему началу и на них построен параллелограмм, то сумма () этих векторов представляет собой диагональ этого параллелограмма, идущую из общего начала векторов и .

 

1. 

Доказательство. Приложим вектор к произвольной точке 0, вектор к концу вектора и вектор к концу вектора .

 

Обозначим буквами A, B, C концы векторов , и , тогда

 

, ч.т.д.

 

3. Существует нулевой вектор такой, что для любого вектора . Это свойство вытекает из определения 1.

4. Для любого вектора существует противоположный ему вектор -такой, что .

 

Для доказательства этого свойства определим вектор -, противоположный вектору , как вектор, коллинеарный вектору , имеющий с ним одинаковую длину и противоположное направление.

 

Взятая по определению 1 сумма вектора с таким вектором -дает нулевой вектор.

 

Определение 2. Разностью вектора и вектора называется такой вектор , который в сумме с вектором дает вектор .

 

Из определения 2 и из правила треугольника (определение 1) сложения векторов вытекает правило построения разности : разность приведенных к общему началу векторов и представляет собой вектор, идущий из конца вычитаемого вектора в конец уменьшаемого вектора .

 

 

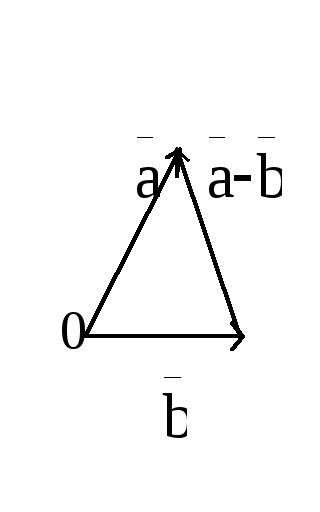
Определение 3. Произведением () вектора на вещественное число  называется вектор , коллинеарный вектору , имеющий длину , и имеющий направление, совпадающее с направлением вектора в случае >0 и противоположное направлению вектора в случае <0.

 

Свойства операции умножения вектора на число:

 

1. .

 

При “растяжении” сторон параллелограмма в  раз в силу свойств подобия диагональ также “растягивается” в  раз, т.е.

 

 .

6. .

7. .

Последние два свойства очевидны из геометрических соображений.