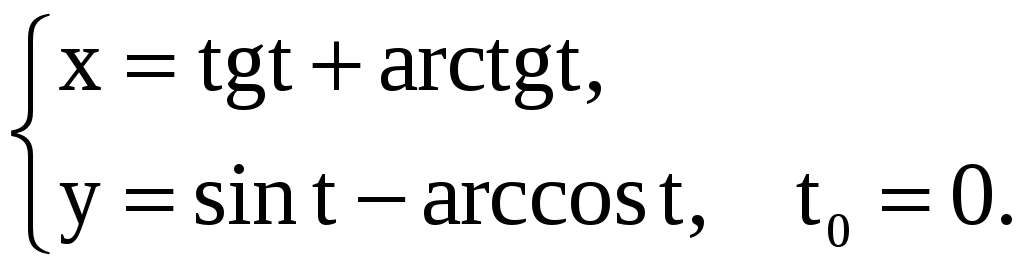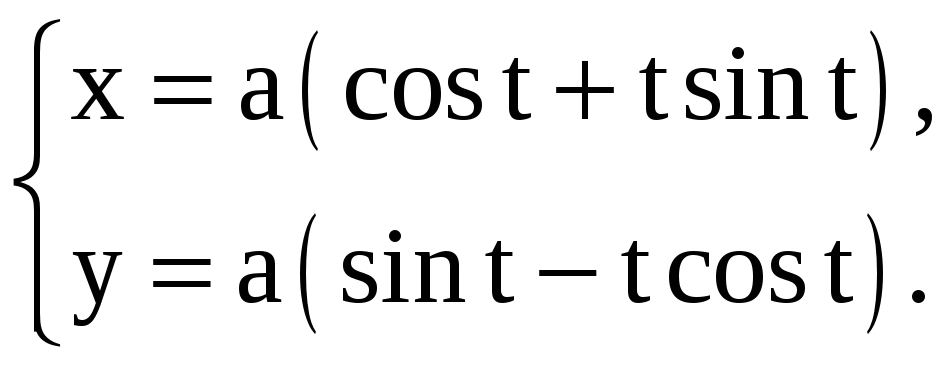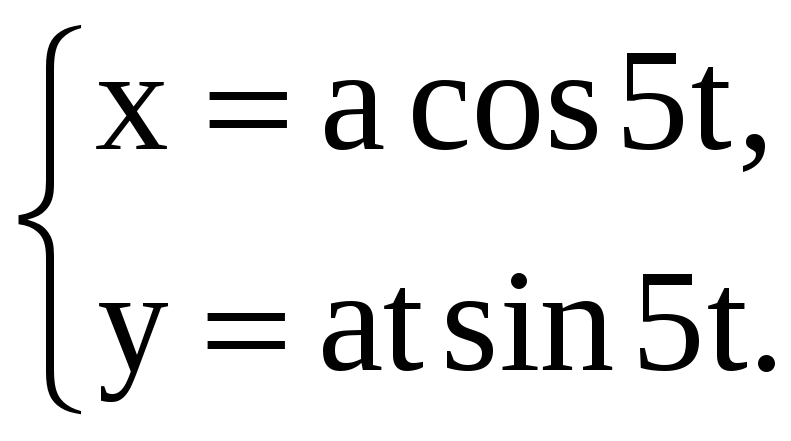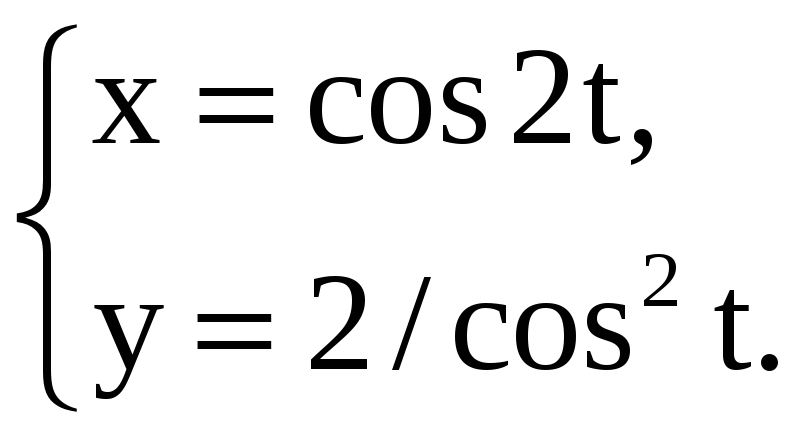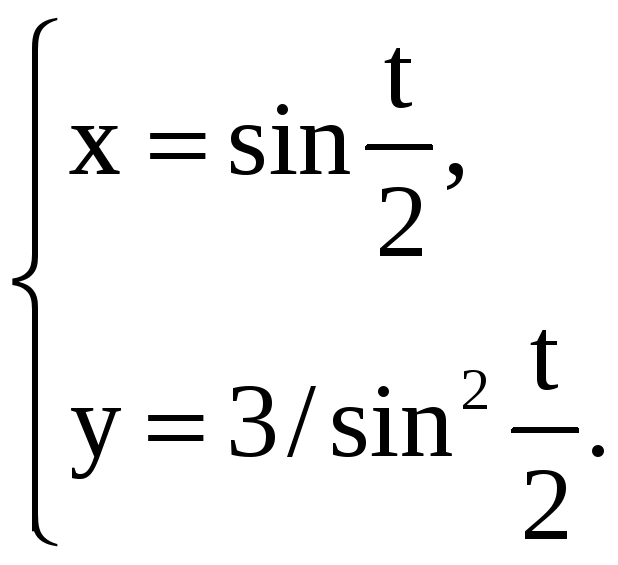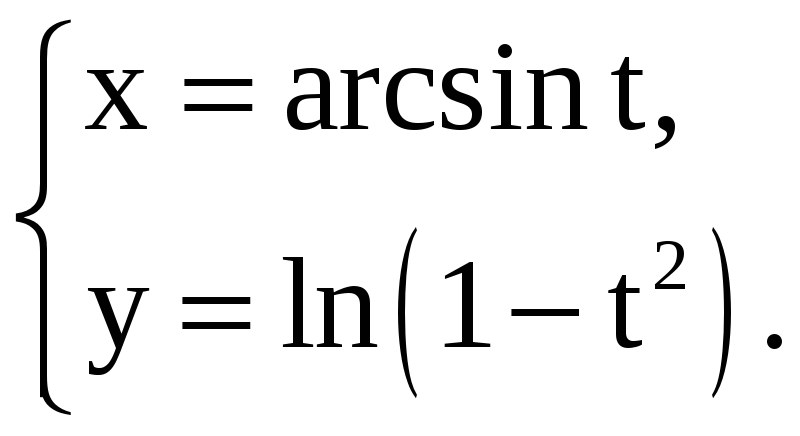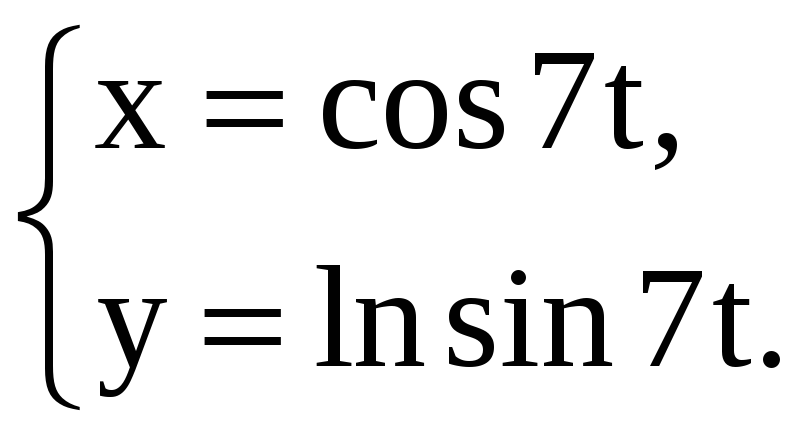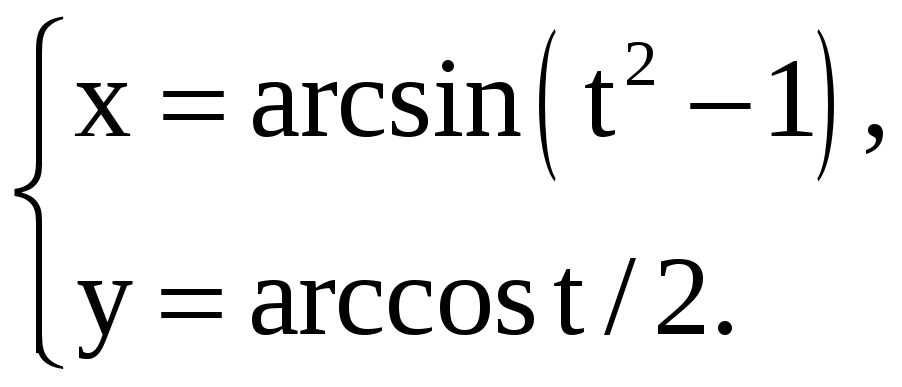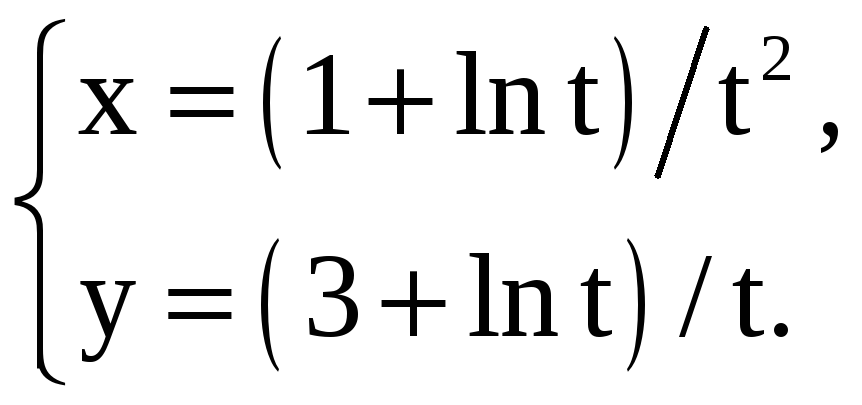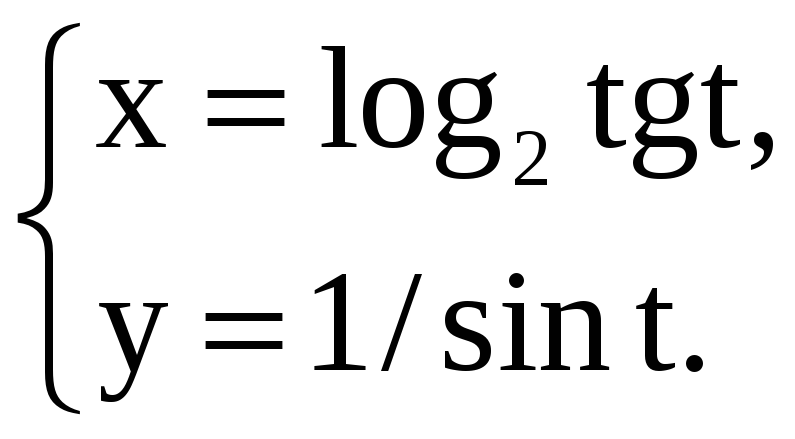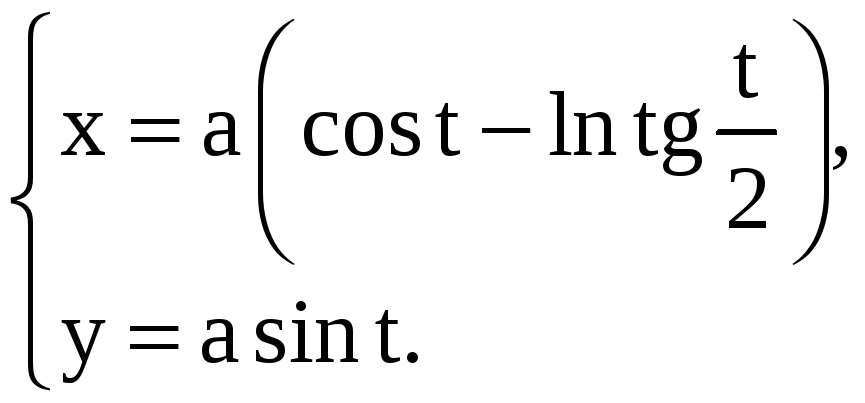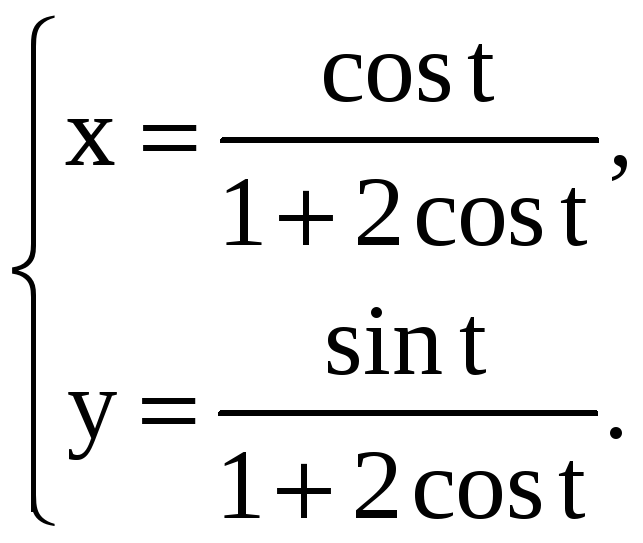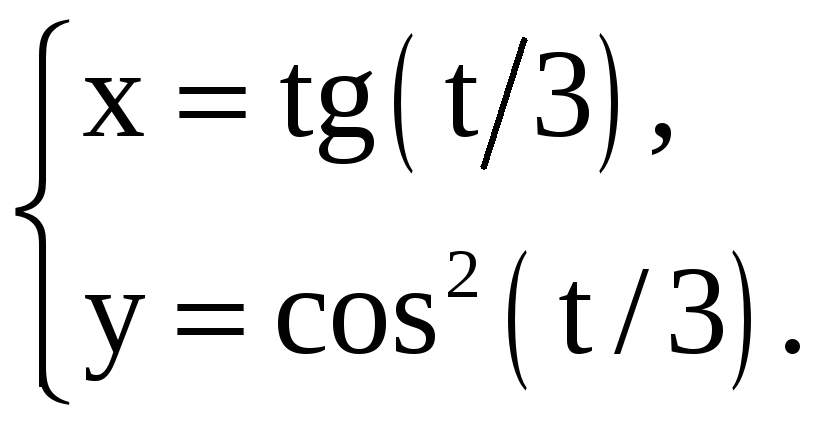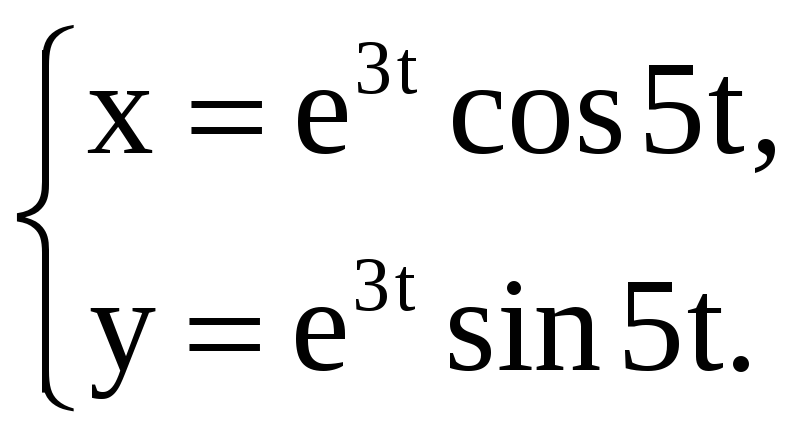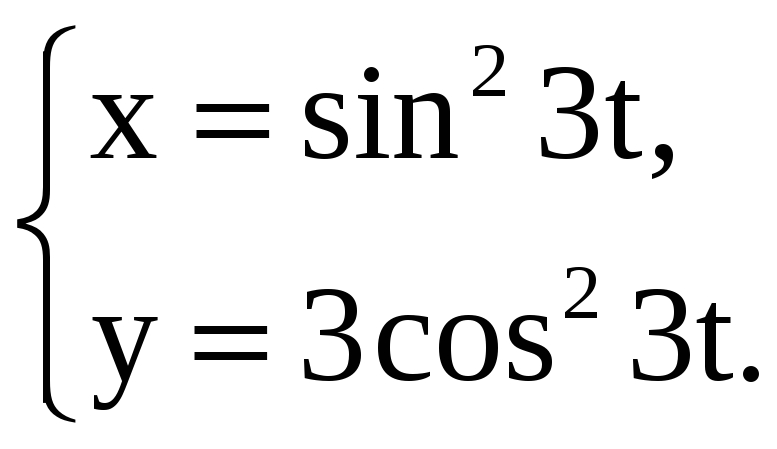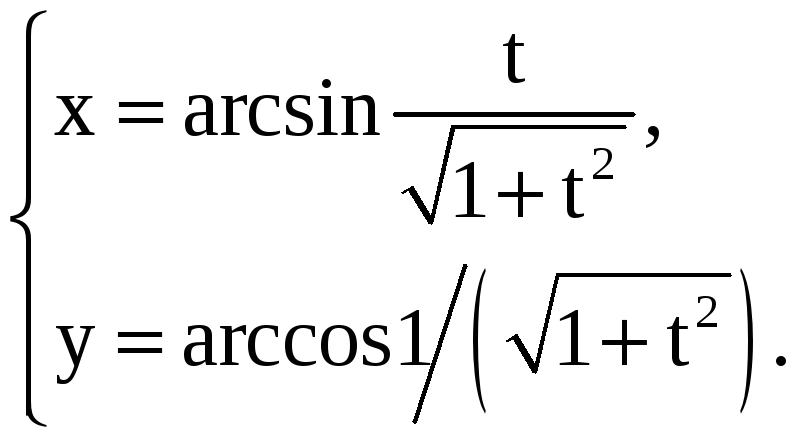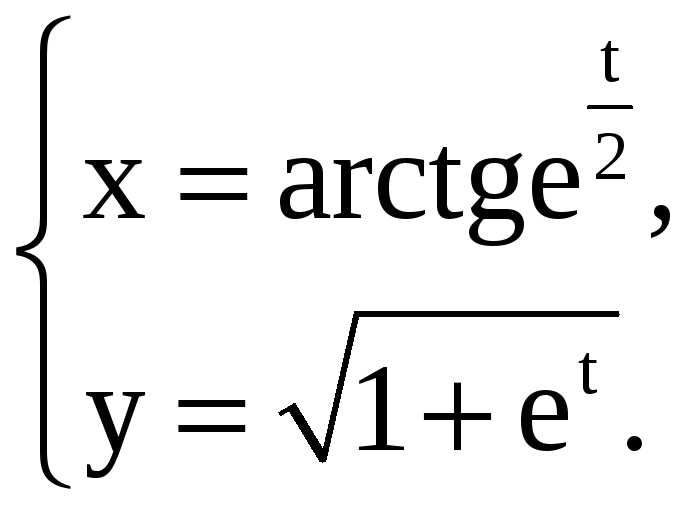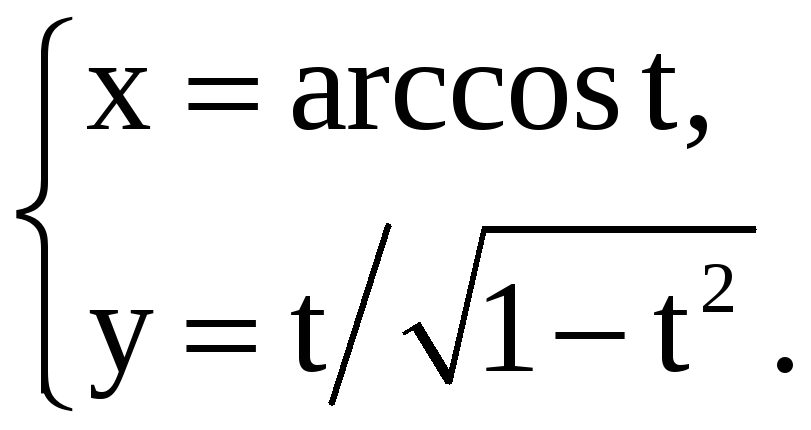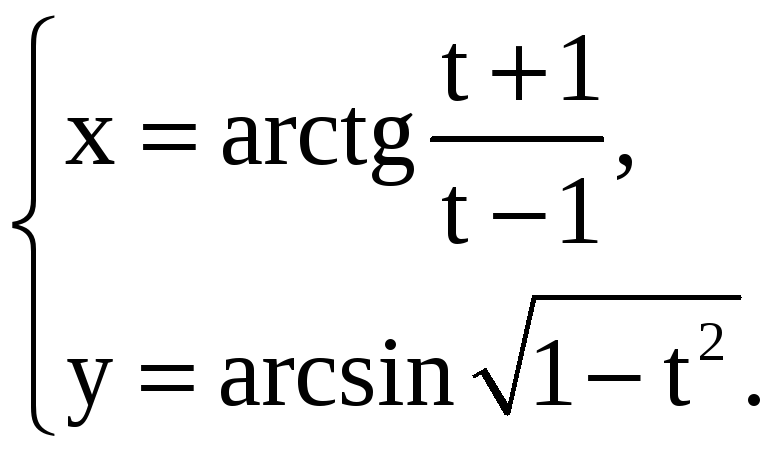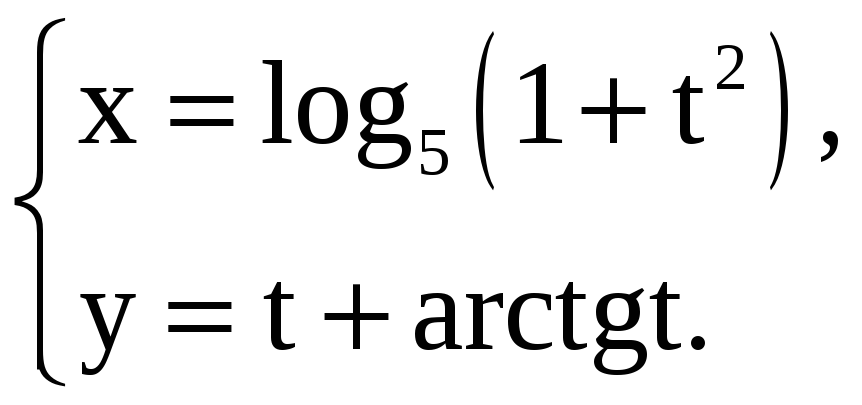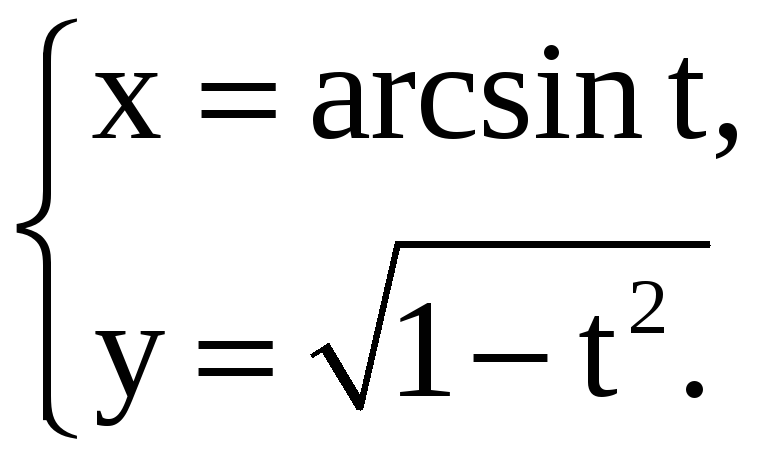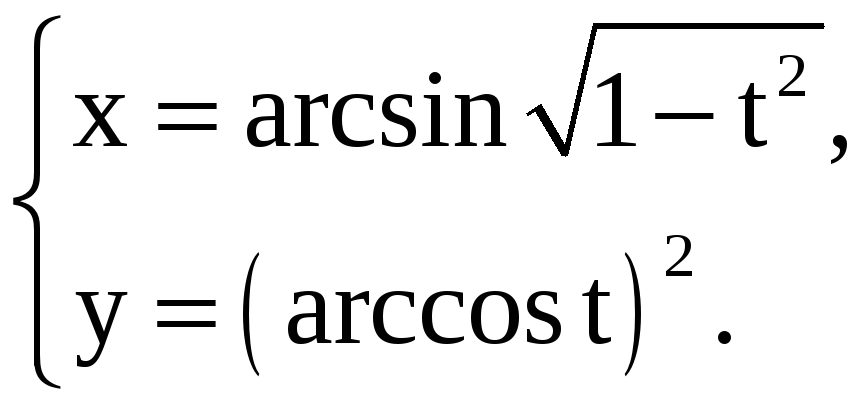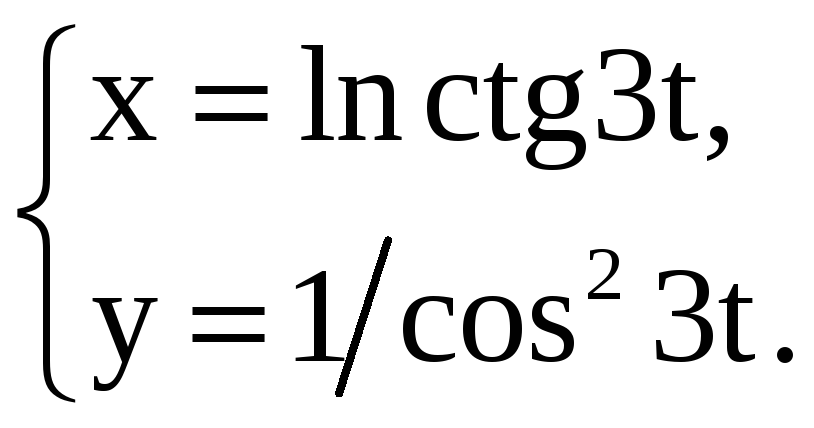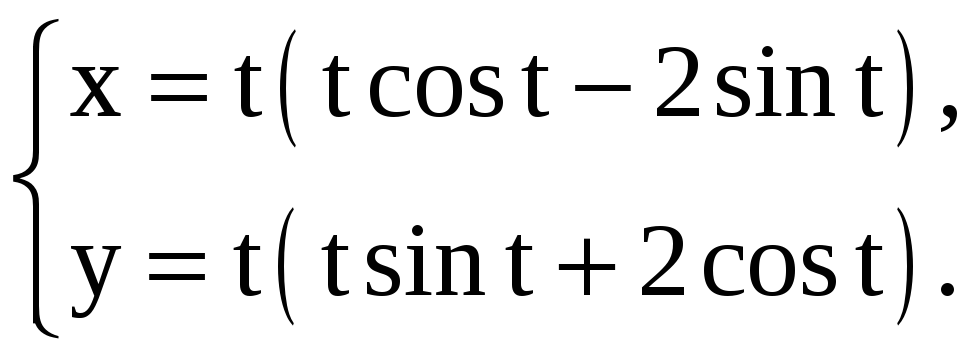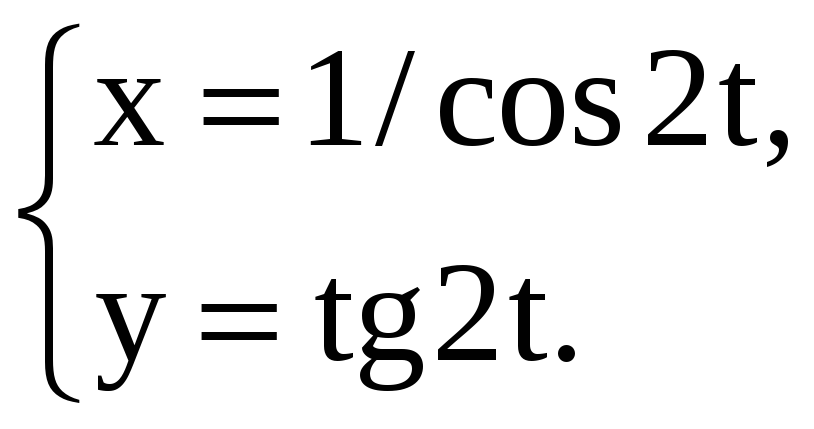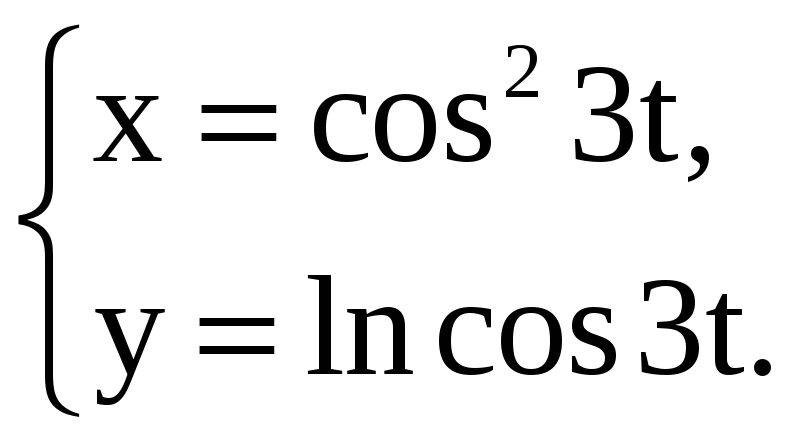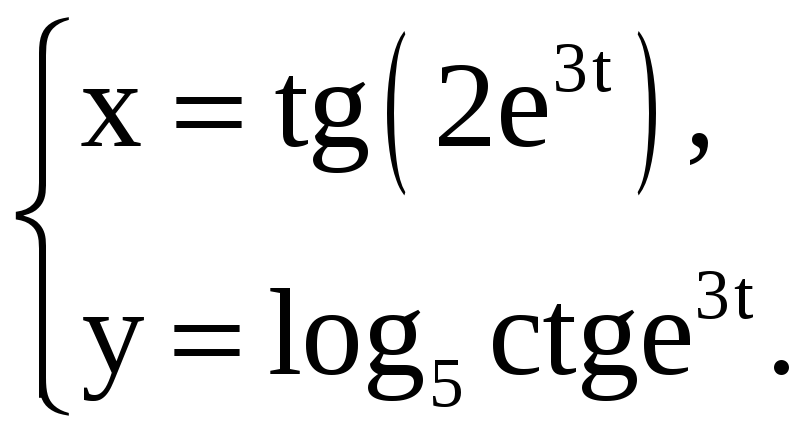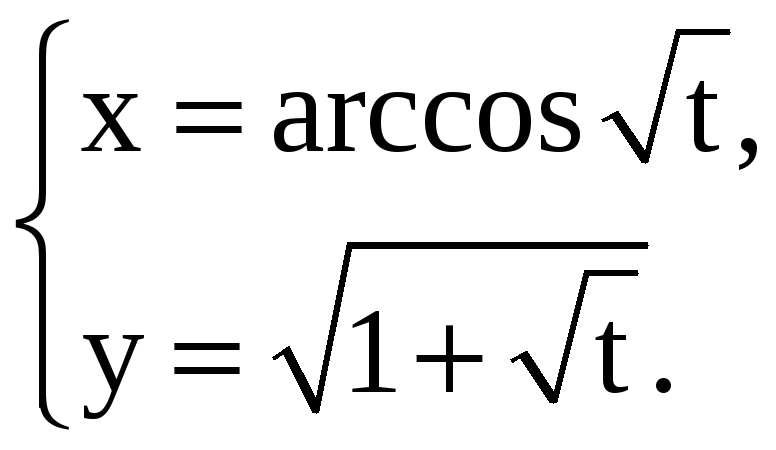- •V. Дифференциальное исчисление функции одного переменного
- •1. Производная. Правила дифференцирования
- •2. Таблица производных
- •3. Правила дифференцирования
- •4. Производные высших порядков
- •5. Дифференцирование функций, заданных неявно или параметрически Говорят, что уравнение
- •6. Уравнения касательной и нормали
- •7. Дифференциал первого порядка
- •8. Дифференциалы высших порядков. Формула Тейлора
- •9. Раскрытие неопределённостей по правилу Лопиталя
- •Задание 5.2
- •Задание 5.3
- •Задание 5.4
- •Задание 5.5
- •Задание 5.6
- •Задание 5.7
- •Задание 5.8
- •Задание 5.14
- •Задание 5.15
- •Задание 5.16
Задание 5.8
Применяя метод логарифмического дифференцирования, найдите производные функций.
1.
a)
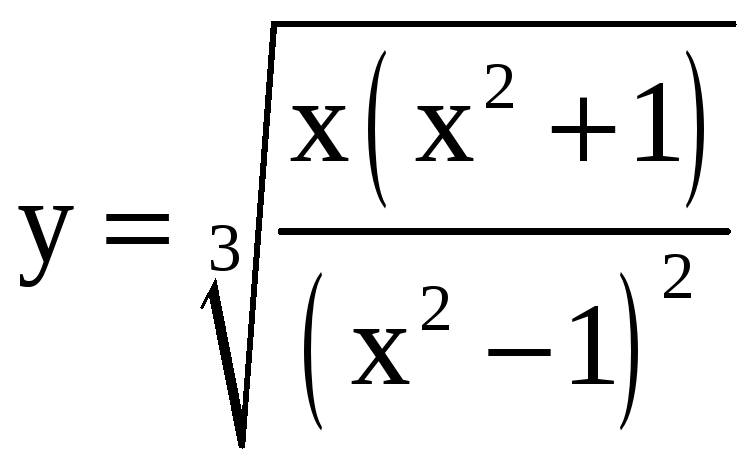 ; б)
; б)
![]() ;
;
2.
a)
![]() ; б)
; б)
![]() ;
;
3.
a)
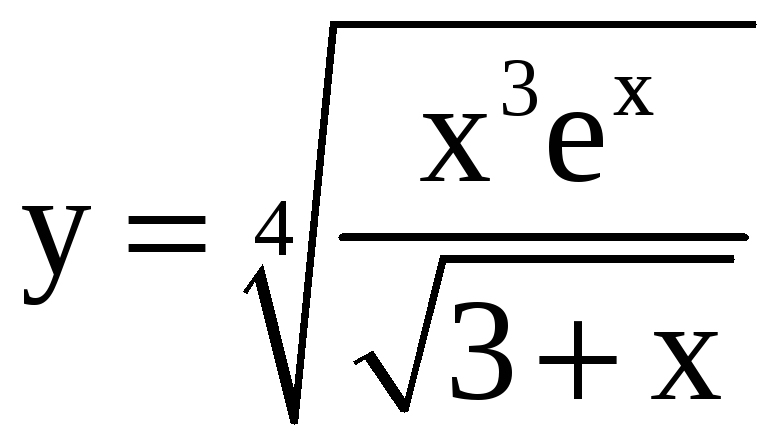 ; б)
; б)
![]() ;
;
4.
a)
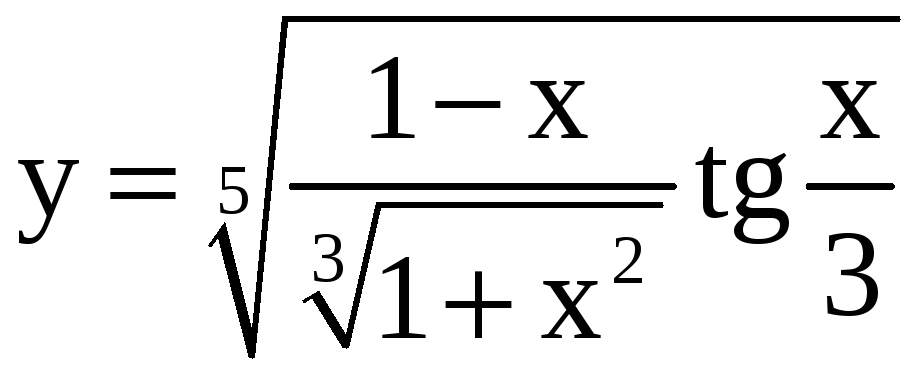 ; б)
; б)
![]() ;
;
5.
a)
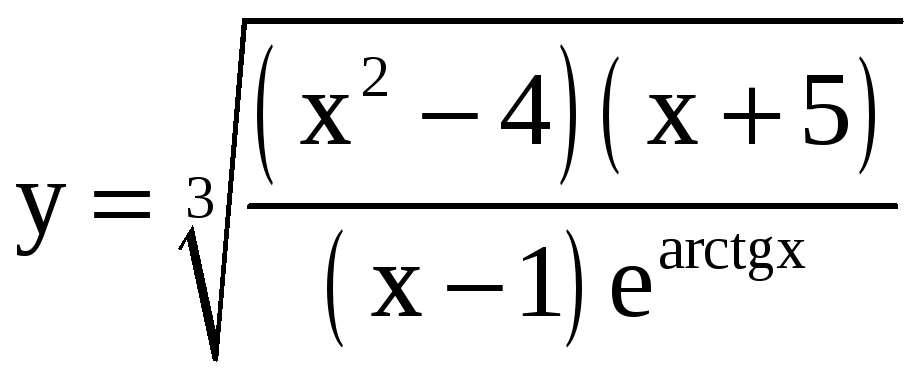 ; б)
; б)
![]() ;
;
6.
a)
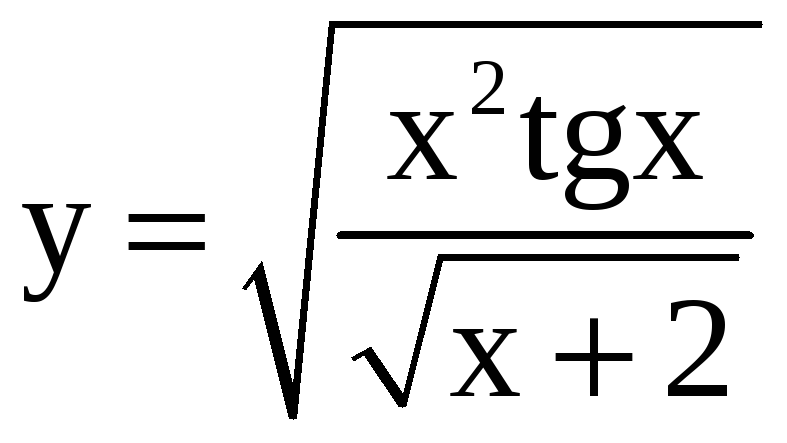 ; б)
; б)
![]() ;
;
7.
a)
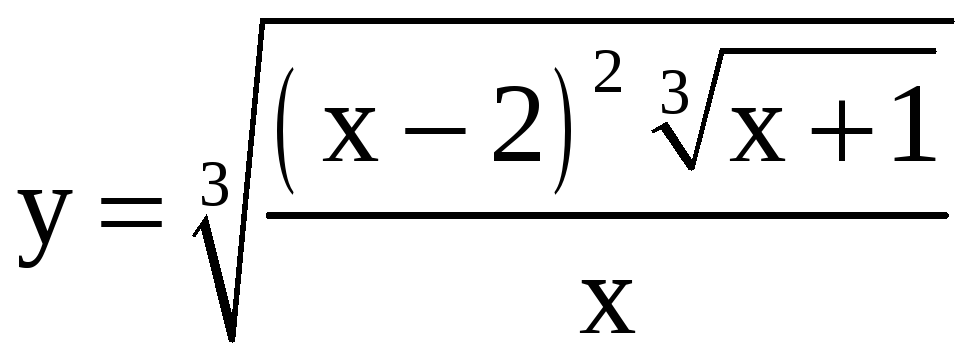 ; б)
; б)
![]() ;
;
8.
a)
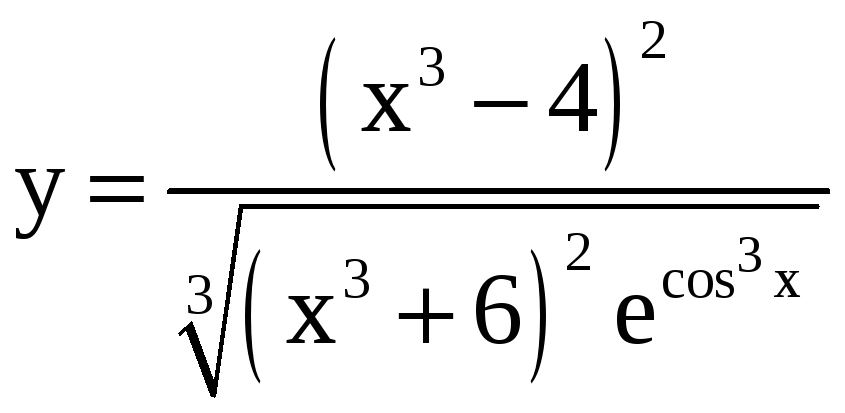 ; б)
; б)
![]() ;
;
9.
a)
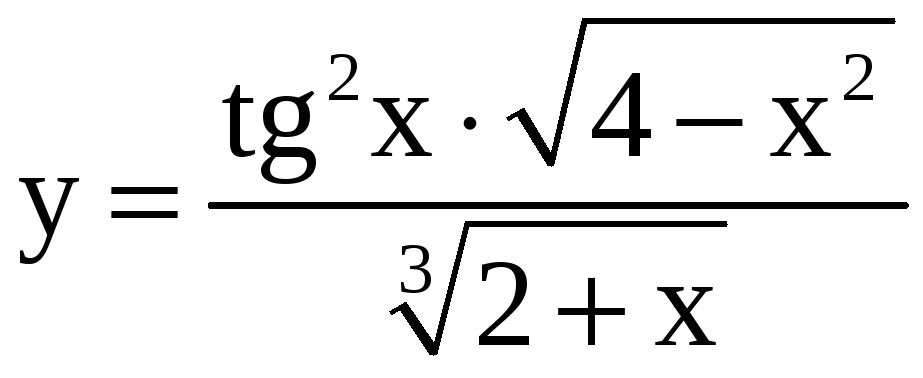 ; б)
; б)
![]() ;
;
10.
a)
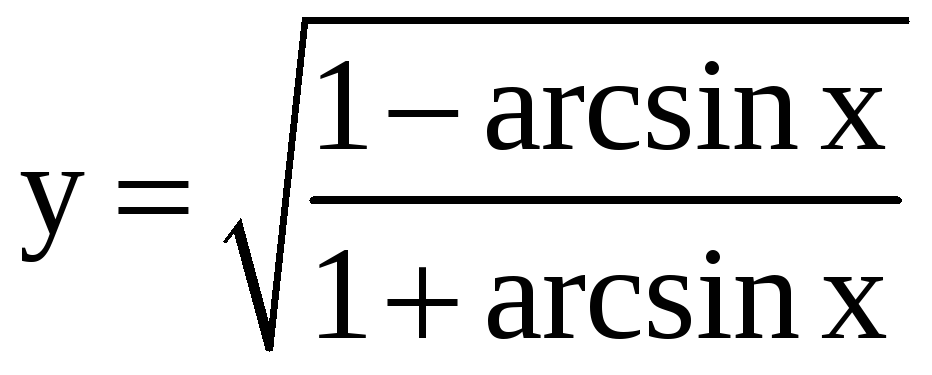 ; б)
; б)
![]() ;
;
11.
a)
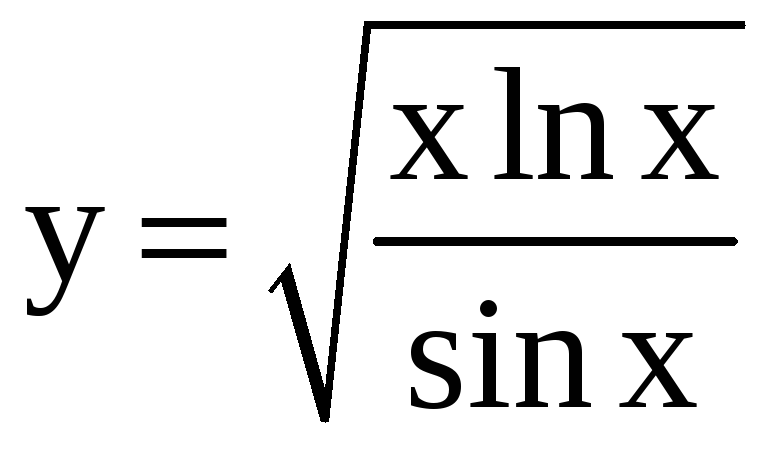 ; б)
; б)
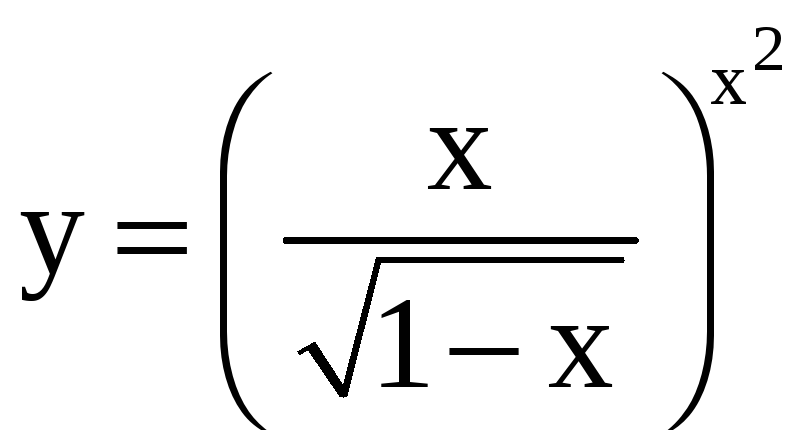 ;
;
12.
a)
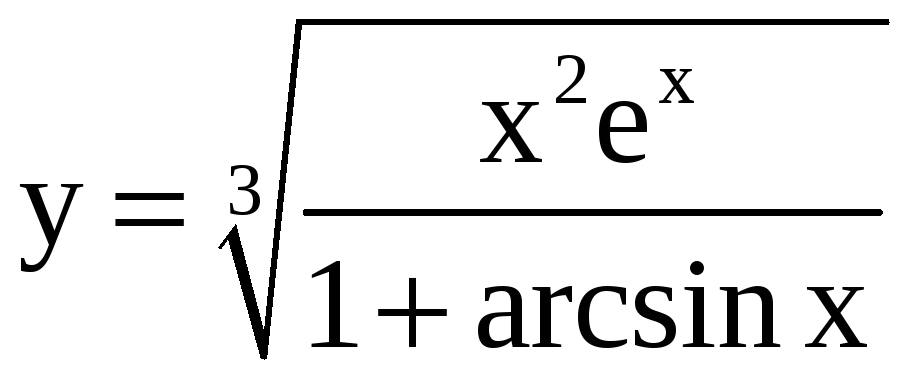 ; б)
; б)
![]() ;
;
13.
a)
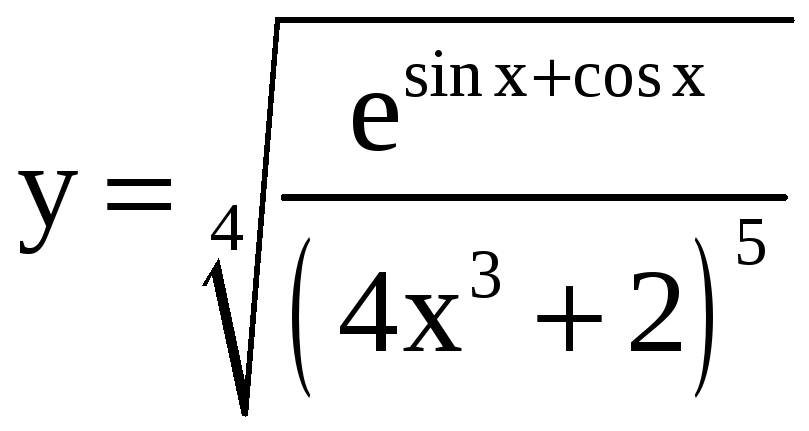 ; б)
; б)
![]() ;
;
14.
a)
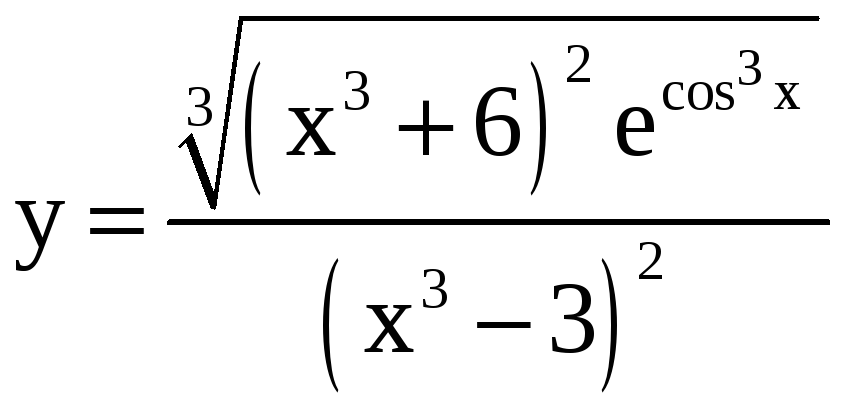 ; б)
; б)
![]() ;
;
15.
a)
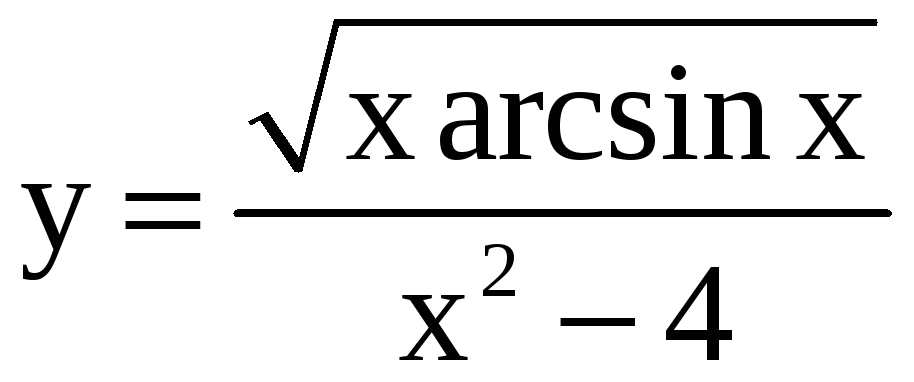 ; б)
; б)
![]() ;
;
16.
a)
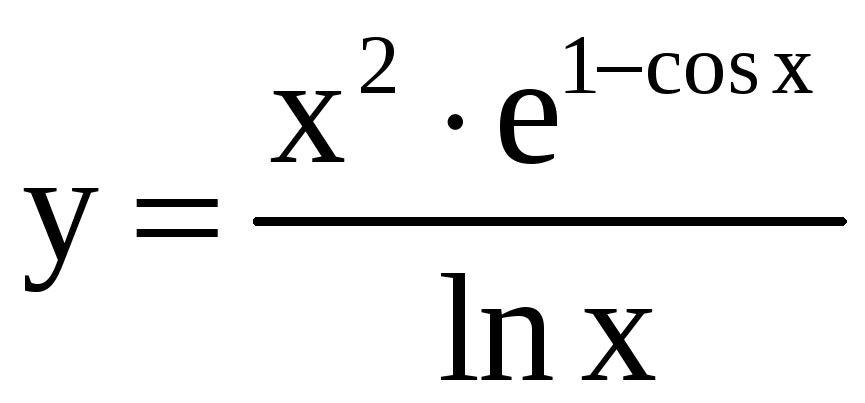 ; б)
; б)
![]() ;
;
17.
a)
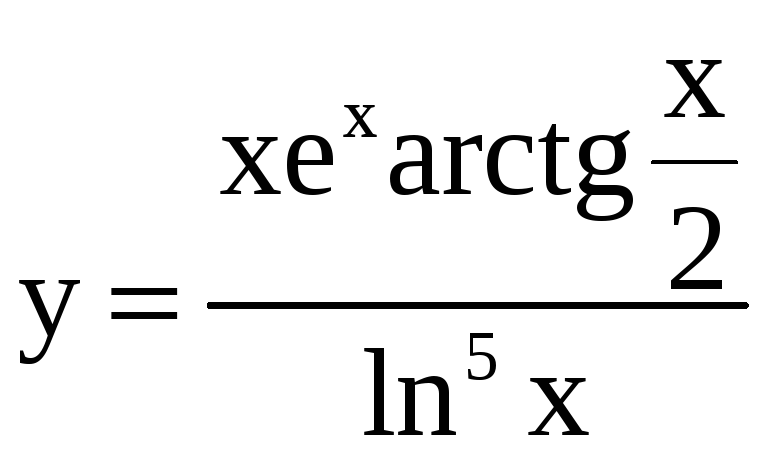 ; б)
; б)
![]() ;
;
18.
a)
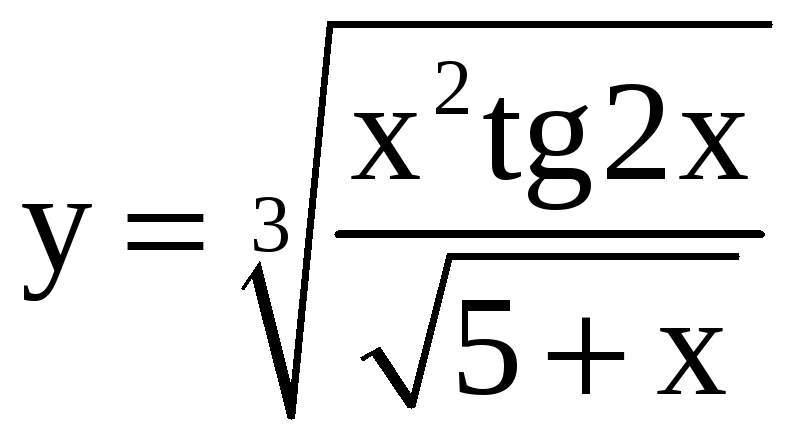 ; б)
; б)
![]() ;
;
19.
a)
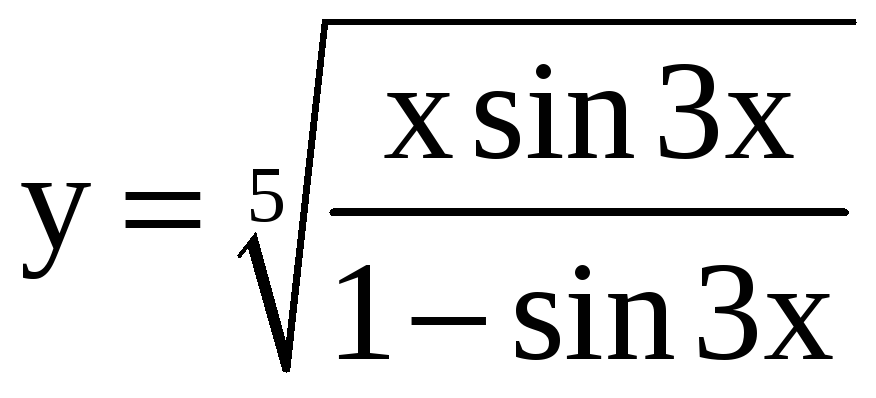 ; б)
; б)
![]() ;
;
20.
a)
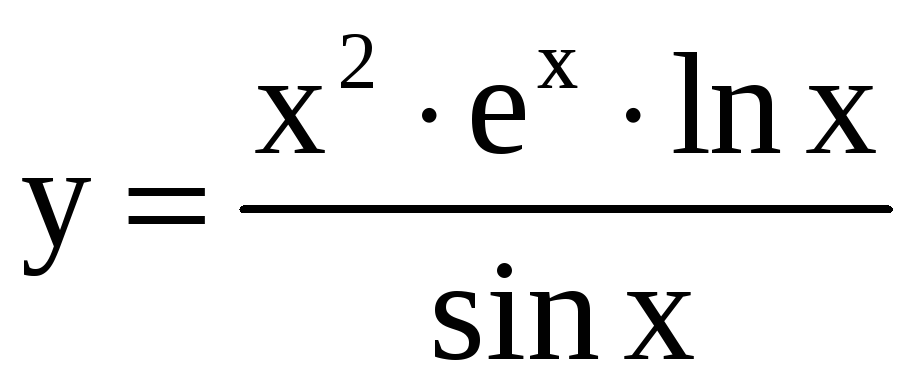 ; б)
; б)
![]() ;
;
21.
a)
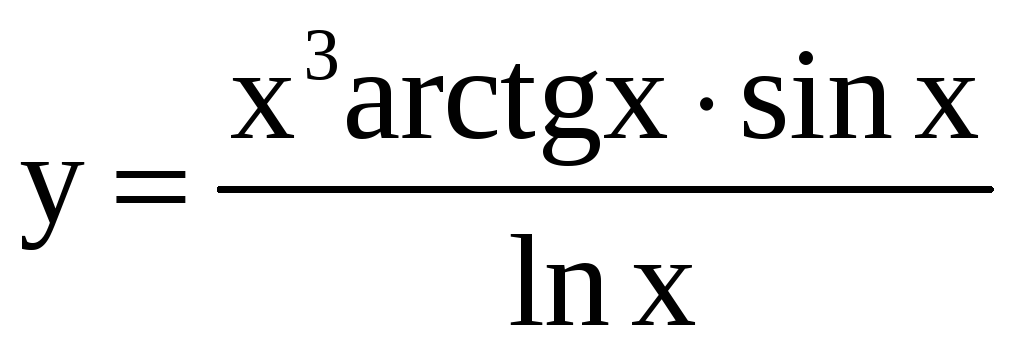 ; б)
; б)
![]() ;
;
22.
a)
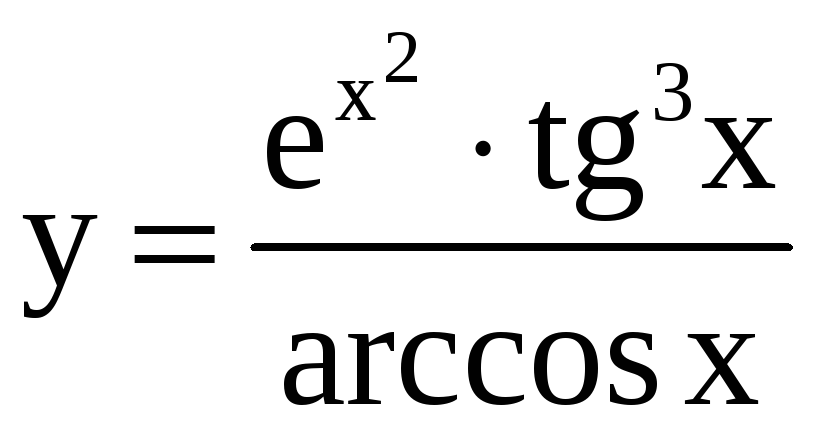 ; б)
; б)
![]() ;
;
23.
a)
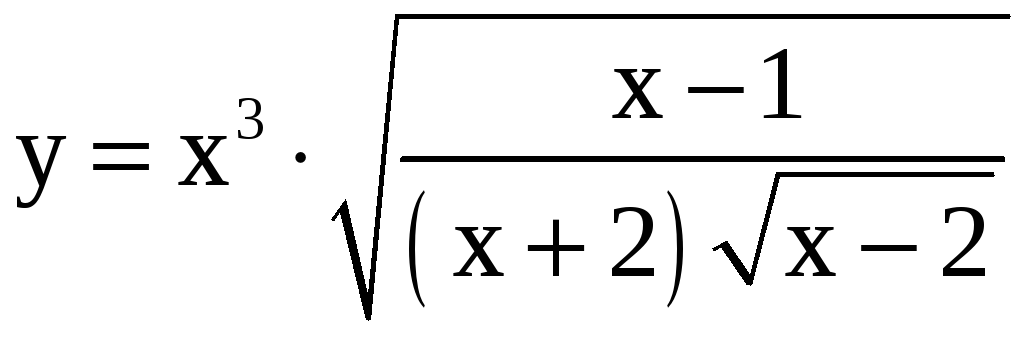 ; б)
; б)
![]() ;
;
24.
a)
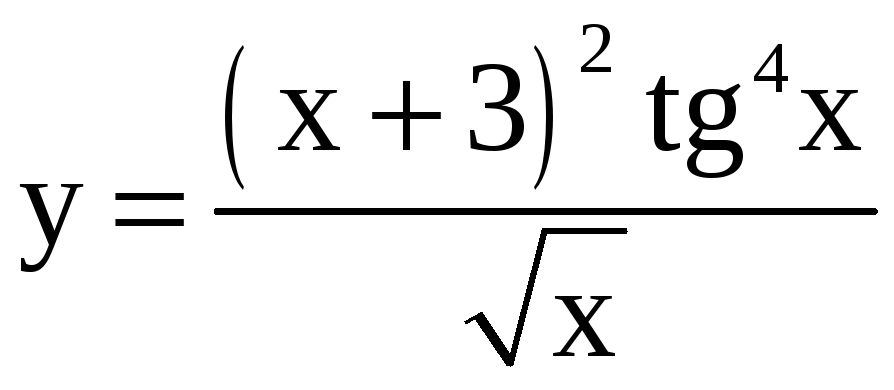 ; б)
; б)
![]() ;
;
25.
a)
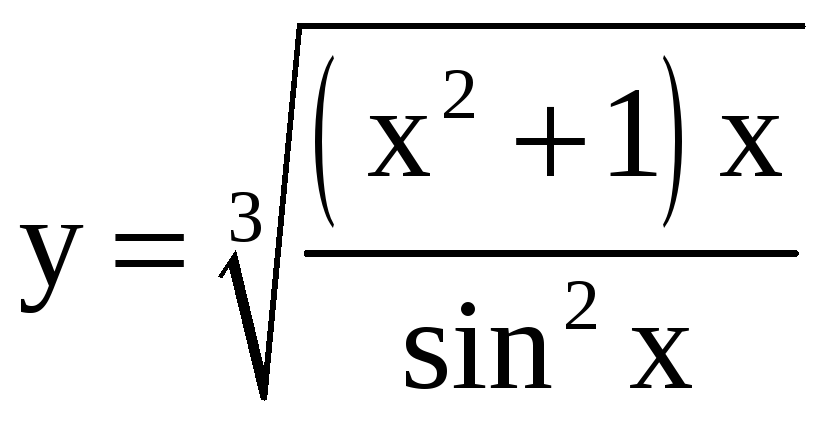 ; б)
; б)
![]() ;
;
26.
a)
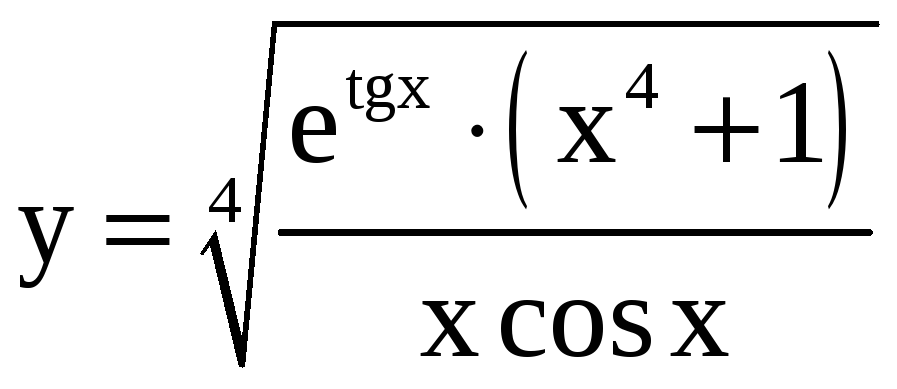 ; б)
; б)
![]() ;
;
27.
a)
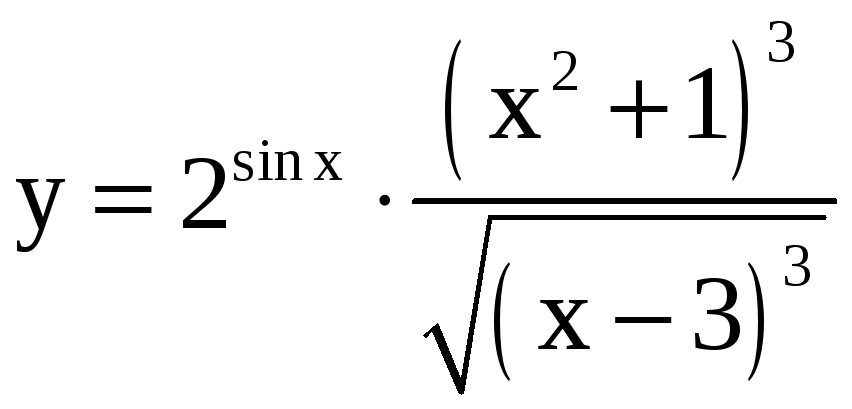 ; б)
; б)
![]() ;
;
28.
a)
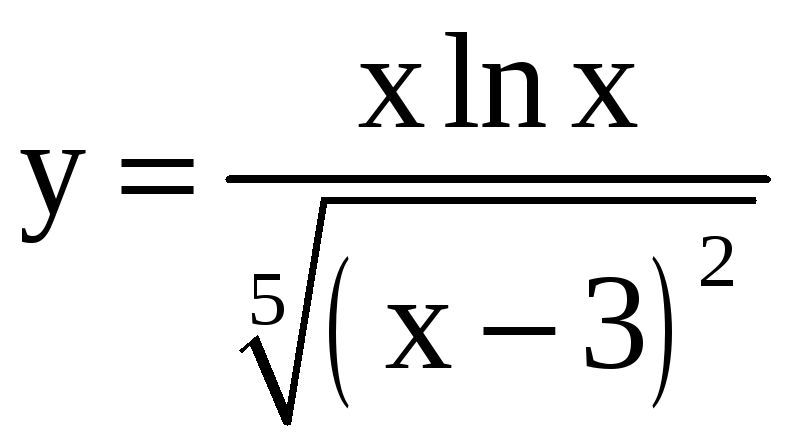 ; б)
; б)
![]() ;
;
29.
a)
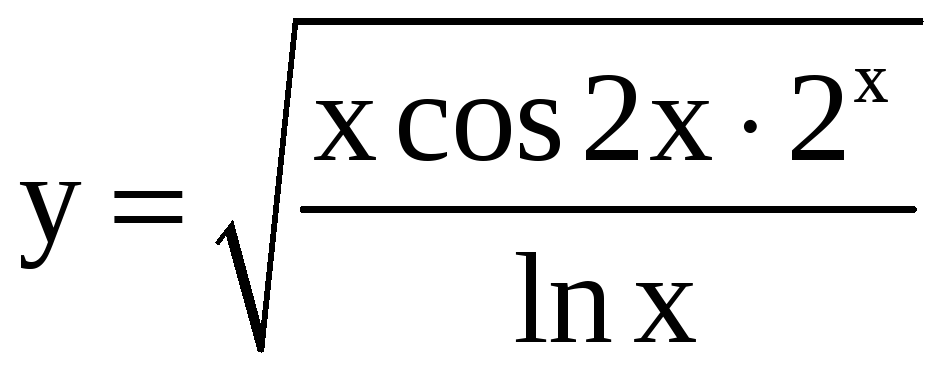 ; б)
; б)
![]() ;
;
30.
a)
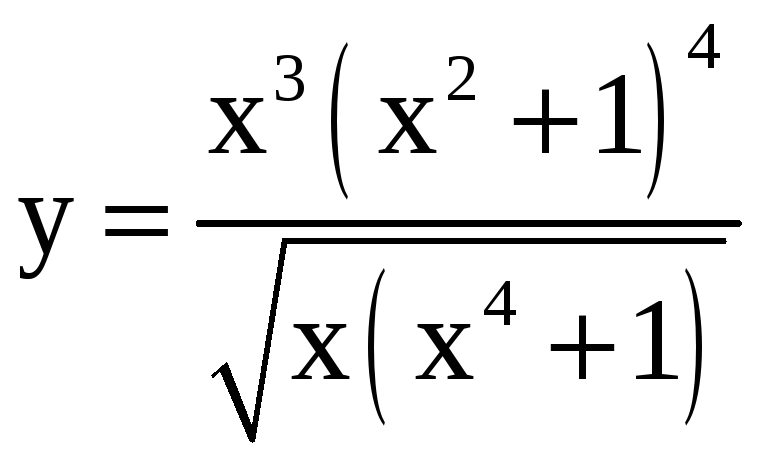 ; б)
; б)
![]() .
.
Задание 5.9
Проверьте, что данная функция удовлетворяет дифференциальному уравнению.
1)
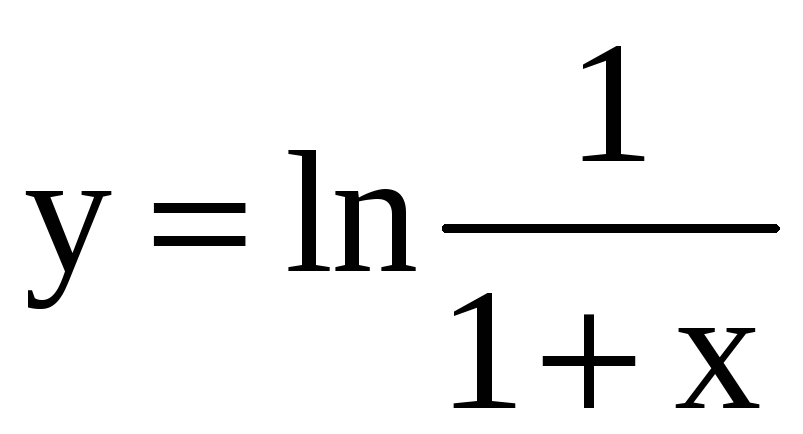 ,
, ![]() ;
;
2)
![]() ,
, ![]() ;
;
3)
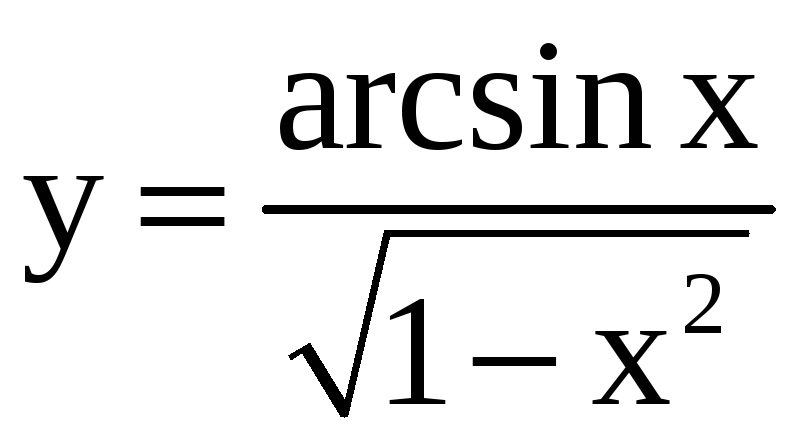 ,
, ![]() ;
;
4)
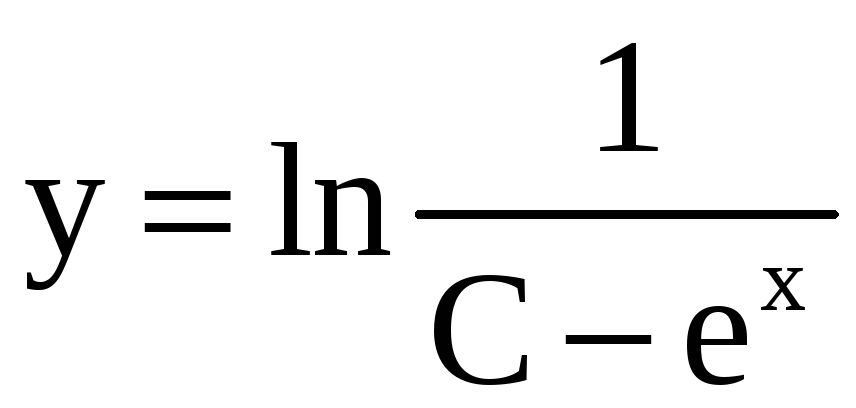 ,
, ![]() ;
;
5)
![]() ,
, ![]() ;
;
6)
![]() ,
, ![]() ;
;
7)
![]() ,
, ![]() ;
;
8)
![]() ,
, ![]() ;
;
9)
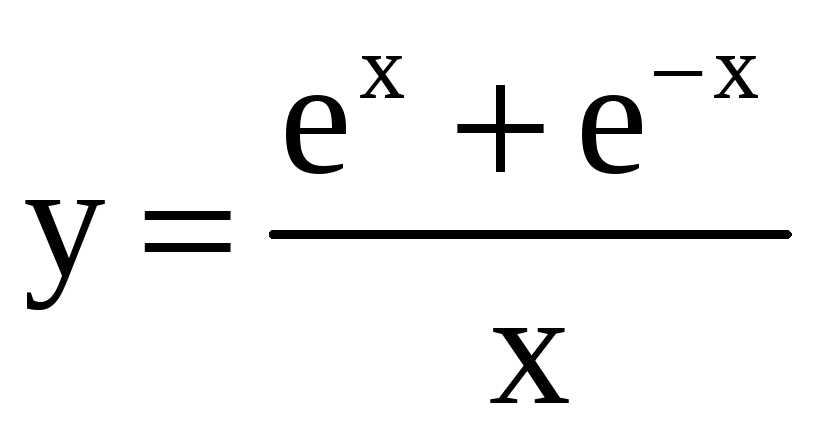 ,
, ![]() ;
;
10)
![]() ,
, ![]() ;
;
11)
![]() ,
, ![]() ;
;
12)
![]() ,
, ![]() ;
;
13)
![]() ,
, ![]() ;
;
14)
![]() ,
, ![]() ;
;
15)
![]() ,
, ![]() ;
;
16)
![]() ,
, ![]() ;
;
17)
![]() ,
, 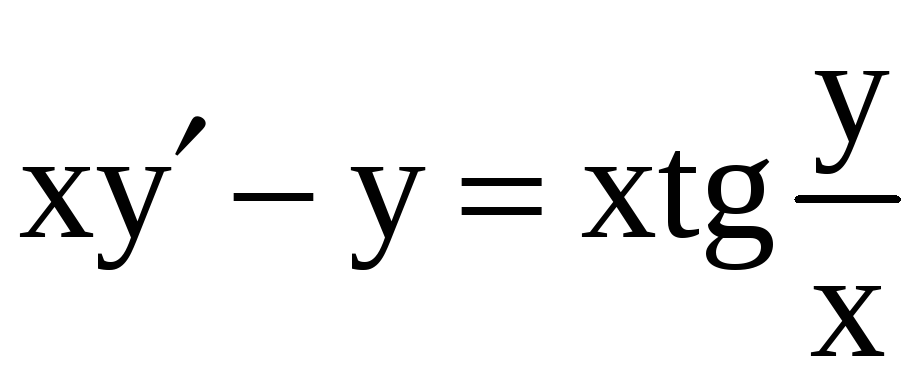 ;
;
18)
![]() ,
, ![]() ;
;
19)
![]() ,
, ![]() ;
;
20)
![]() ,
, ![]() ;
;
21)
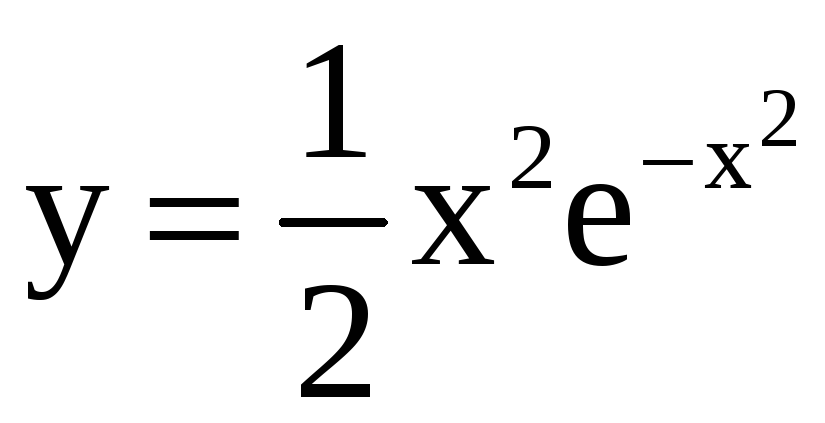 ,
, ![]() ;
;
22)
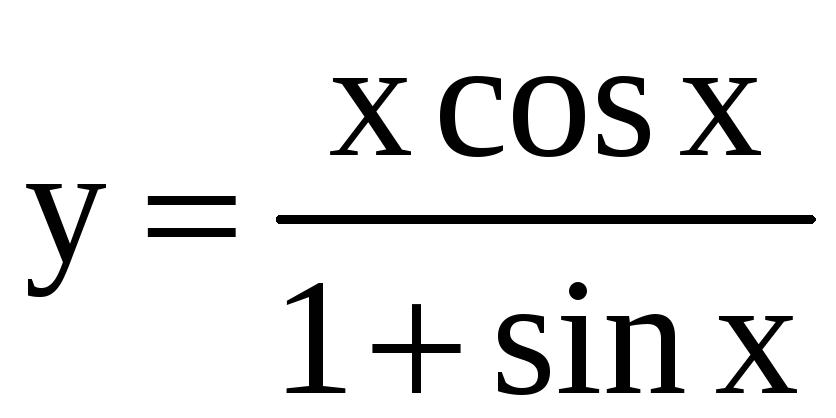 ,
, ![]() ;
;
23)
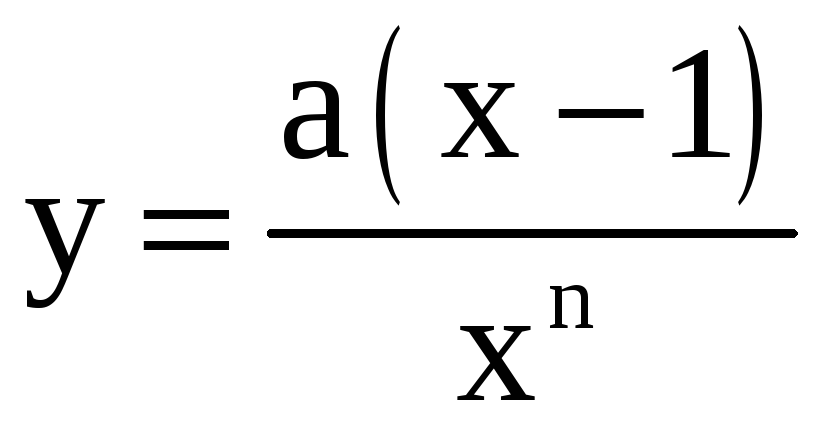 ,
, 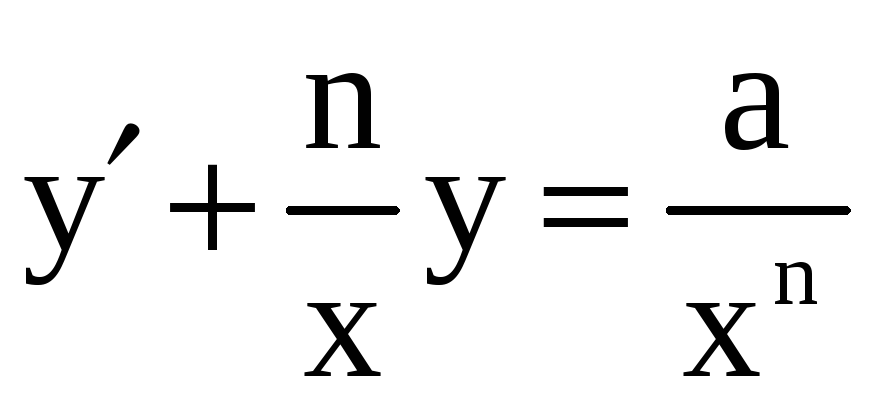 ;
;
24)
![]() ,
, ![]() ;
;
25)
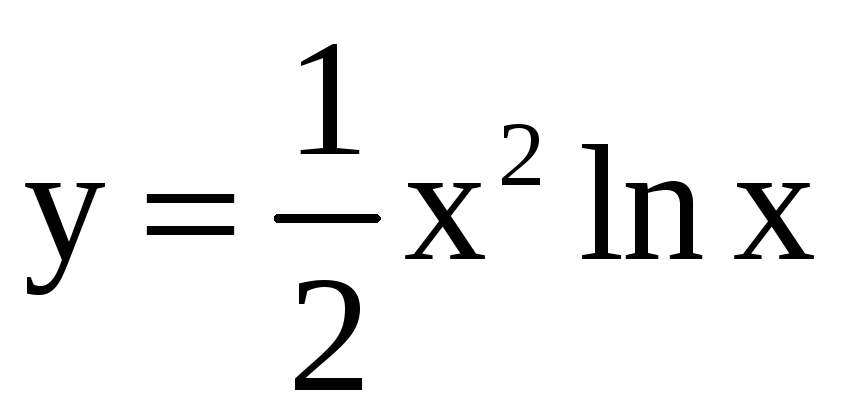 ,
, 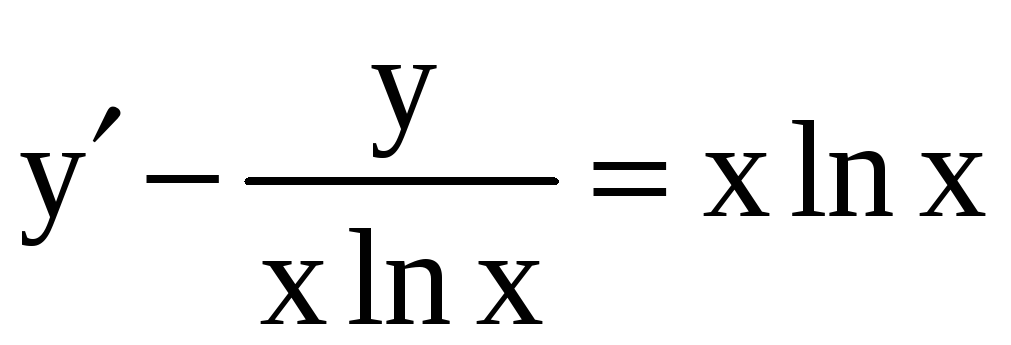 ;
;
26)
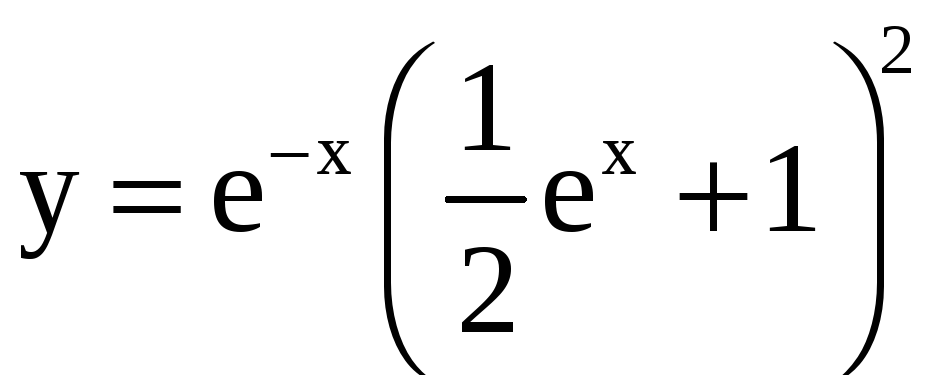 ,
, ![]() ;
;
27)
![]() ,
, ![]() ;
;
28)
![]() ,
, ![]() ;
;
29)
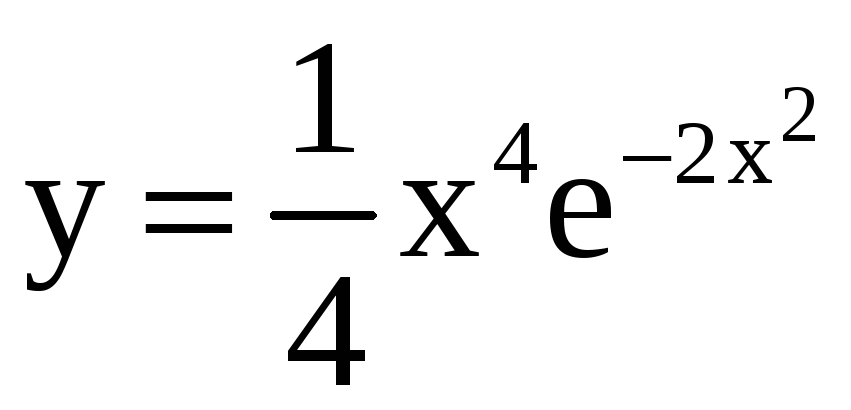 ,
, ![]() ;
;
30)
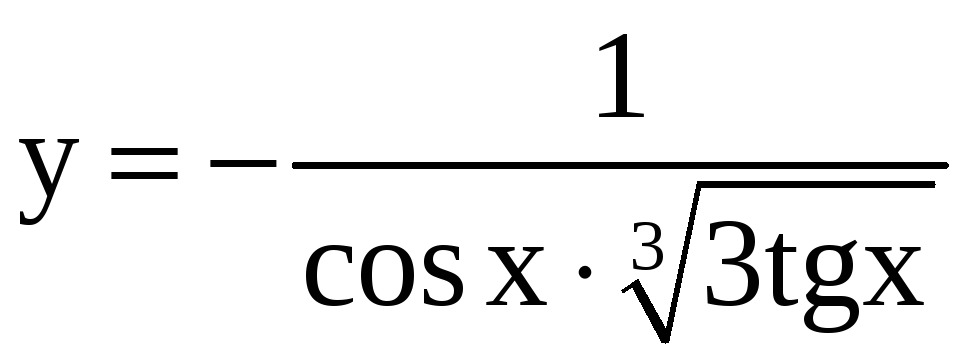 ,
, ![]() .
.
Задание 5.10
Найдите
![]() ,
,
![]() .
.
1)
![]() ; 11)
; 11)
![]() ; 21)
; 21)
![]() ;
;
2)
![]() ; 12)
; 12)
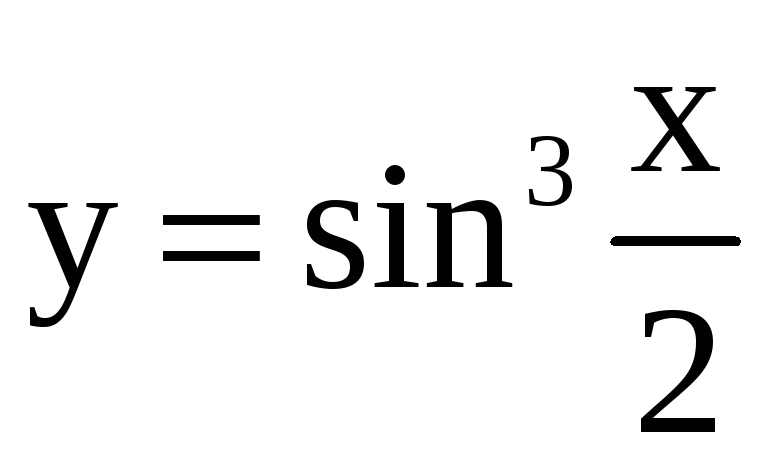 ; 22)
; 22)
![]() ;
;
3)
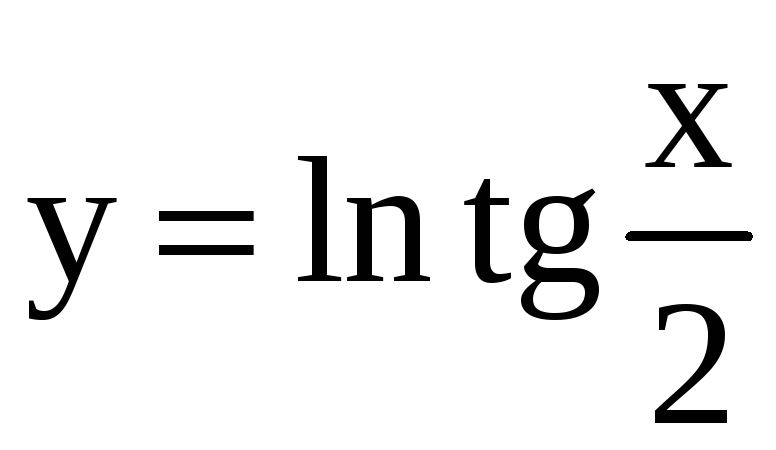 ; 13)
; 13)
![]() ; 23)
; 23)
![]() ;
;
4)
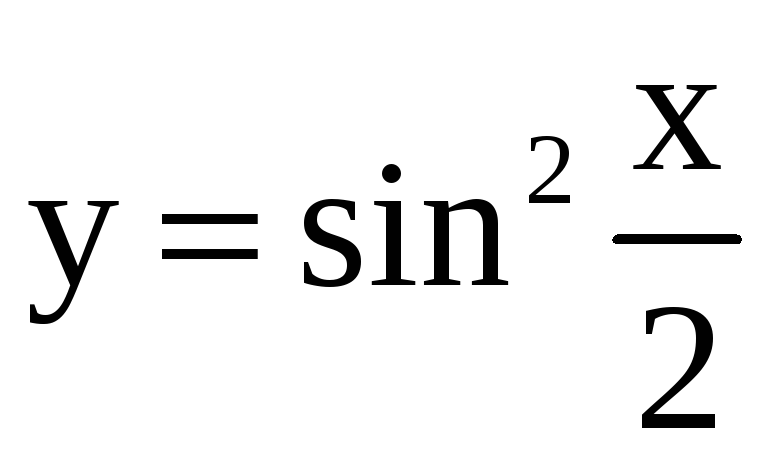 ; 14)
; 14)
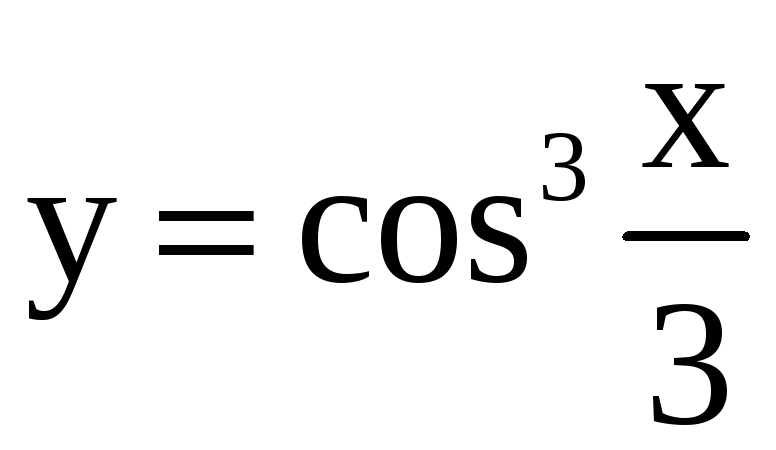 ; 24)
; 24)
![]() ;
;
5)
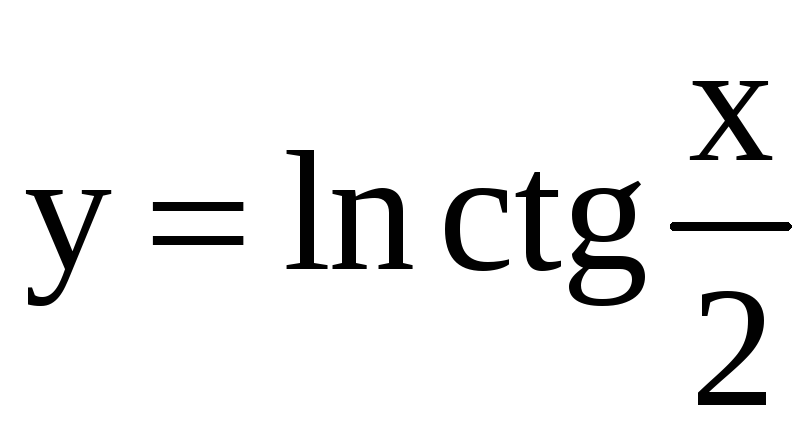 ; 15)
; 15)
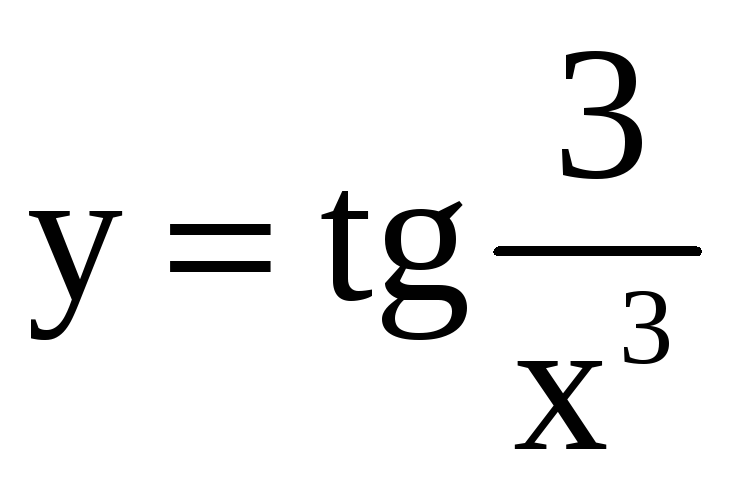 ; 25)
; 25)
![]() ;
;
6)
![]() ; 16)
; 16)
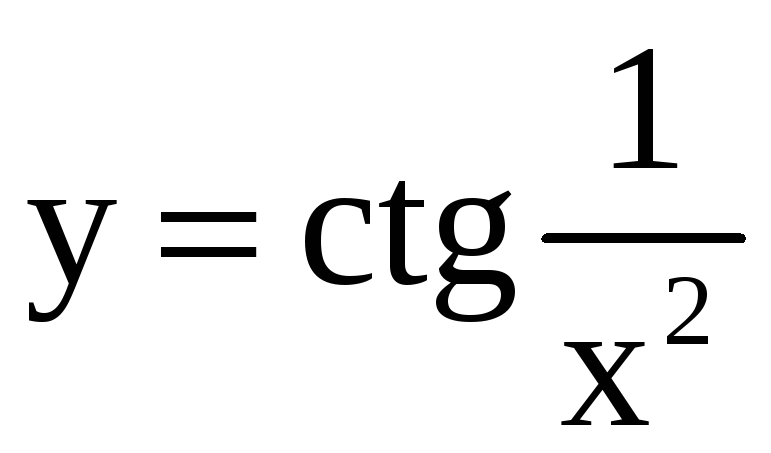 ; 26)
; 26)
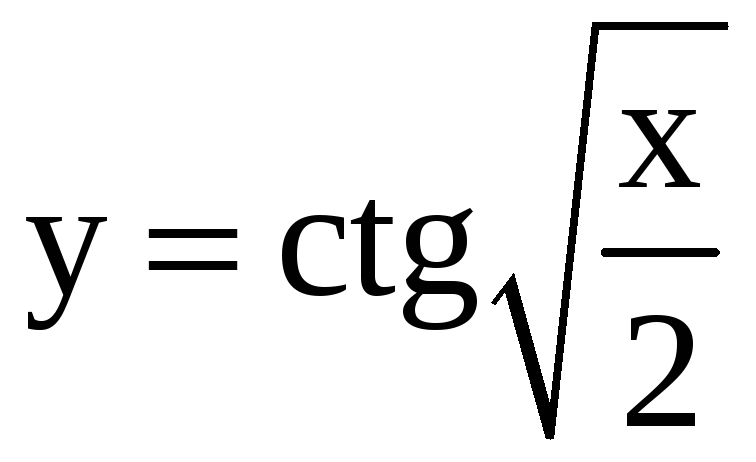 ;
;
7)
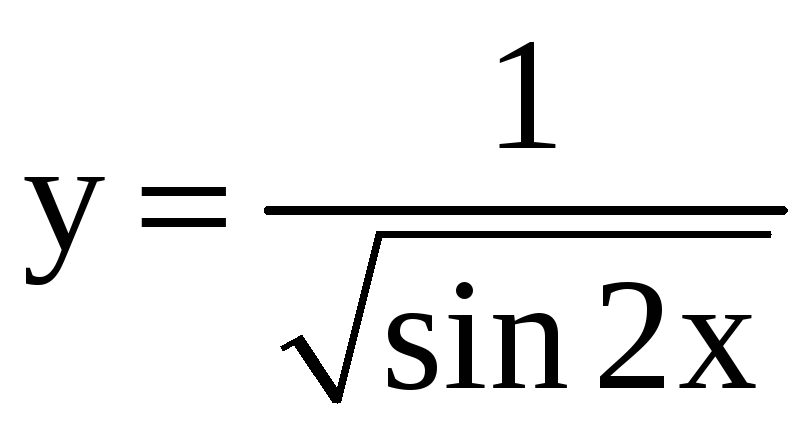 ; 17)
; 17)
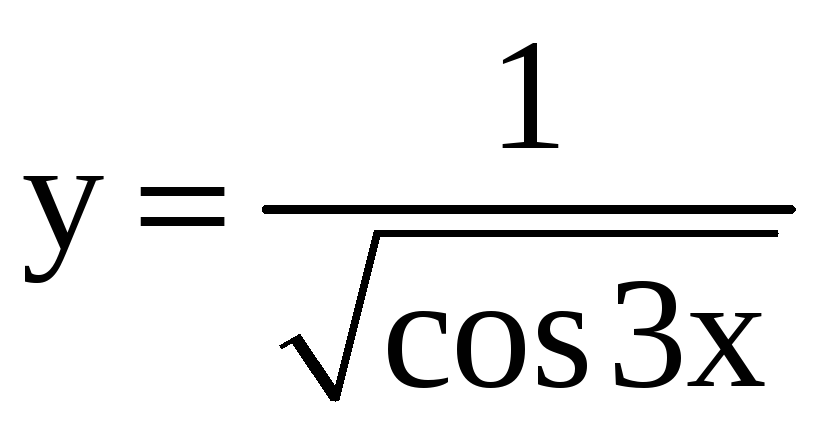 ; 27)
; 27)
![]() ;
;
8)
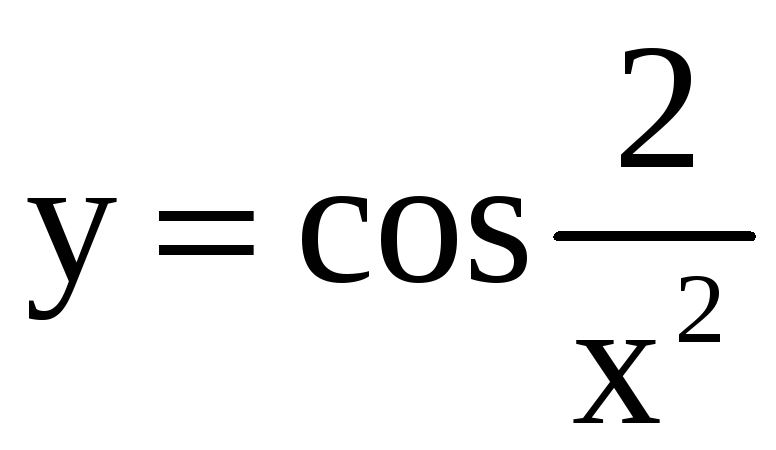 ; 18)
; 18)
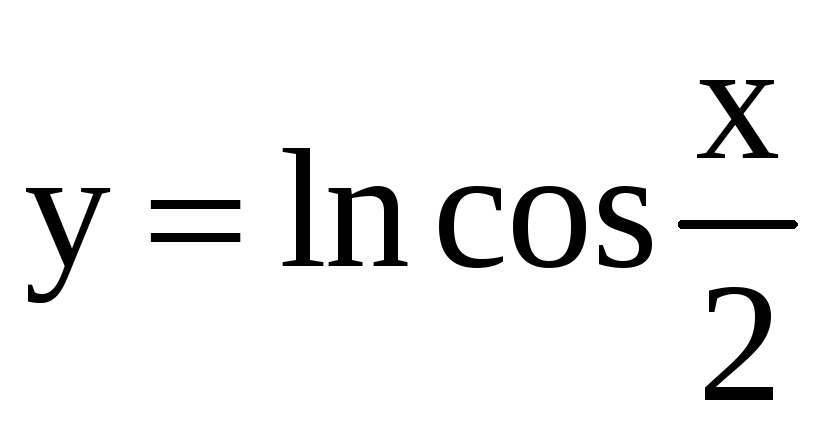 ; 28)
; 28)
![]() ;
;
9)
![]() ; 19)
; 19)
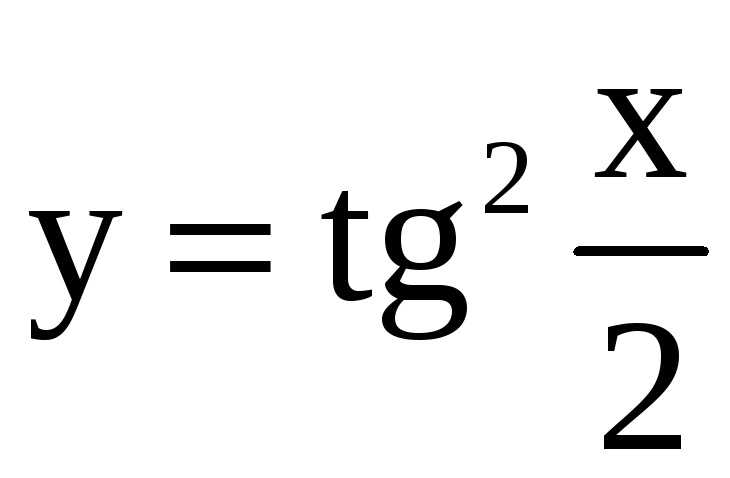 ; 29)
; 29)
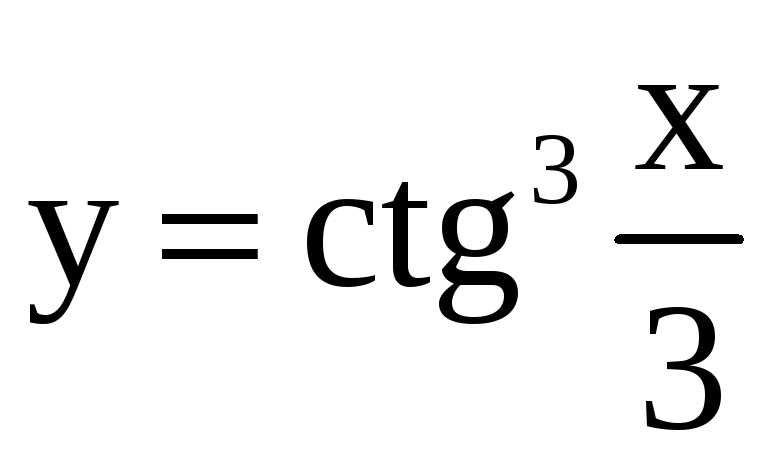 ;
;
10)
![]() ; 20)
; 20)
![]() ; 30)
; 30)
![]() .
.
Задание 5.11
Найдите производную n-го порядка.
1)
![]() ; 16)
; 16)
![]() ;
;
2)
![]() ; 17)
; 17)
![]() ;
;
3)
![]() ; 18)
; 18)
![]() ;
;
4)
![]() ; 19)
; 19)
![]() ;
;
5)
![]() ; 20)
; 20)
![]() ;
;
6)
![]() ; 21)
; 21)
![]() ;
;
7)
![]() ; 22)
; 22)
![]() ;
;
8)
![]() ; 23)
; 23)
![]() ;
;
9)
![]() ; 24)
; 24)
![]() ;
;
10)
![]() ; 25)
; 25)
![]() ;
;
11)
![]() ; 26)
; 26)
![]() ;
;
12)
![]() ; 27)
; 27)
![]() ;
;
13)
![]() ; 28)
; 28)
![]() ;
;
14)
![]() ; 29)
; 29)
![]() ;
;
15)
![]() ; 30)
; 30)
![]() .
.
Задание 5.12
Найдите производную третьего порядка.
1)
![]() ;
3)
;
3)
![]() ;
;
2)
![]() ;
4)
;
4)
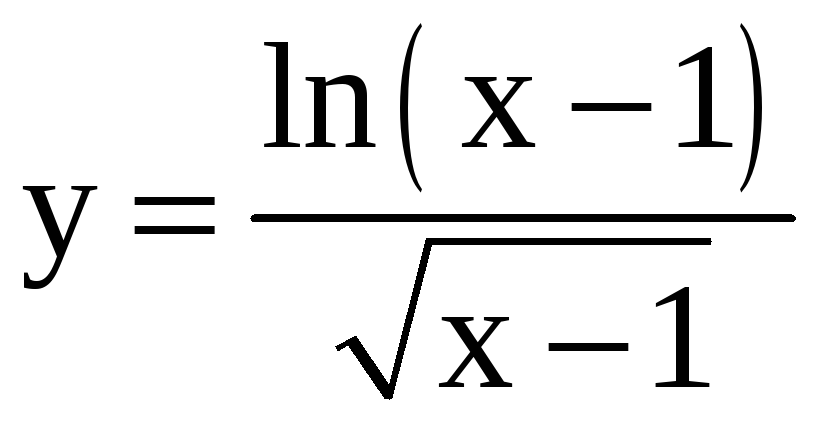 ;
;
5)
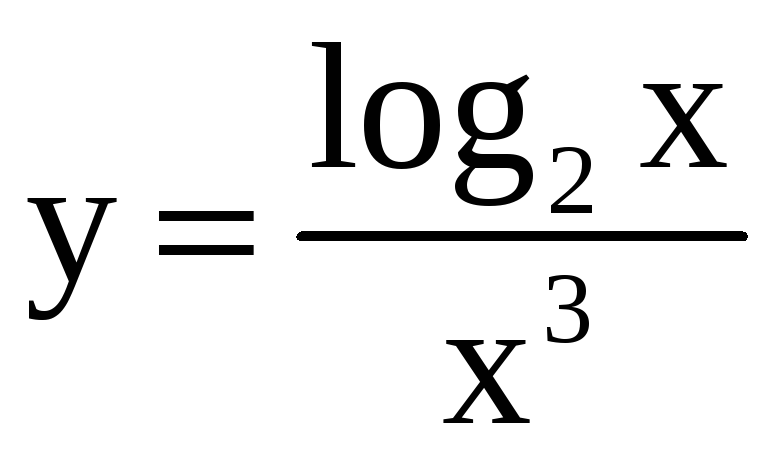 ; 18)
; 18)
![]() ;
;
6)
![]() ; 19)
; 19)
![]() ;
;
7)
![]() ;
20)
;
20)
![]() ;
;
8)
![]() ; 21)
; 21)
![]() ;
;
9)
![]() ; 22)
; 22)
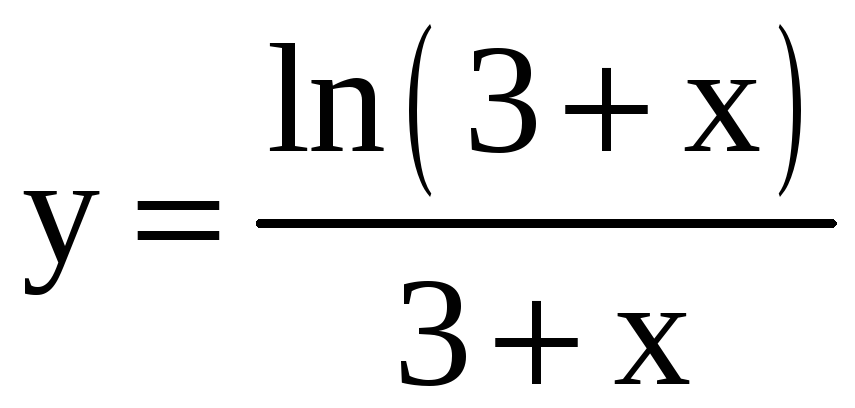 ;
;
10)
![]() ; 23)
; 23)
![]() ;
;
11)
![]() ; 24)
; 24)
![]() ;
;
12)
![]() ; 25)
; 25)
![]() ;
;
13)
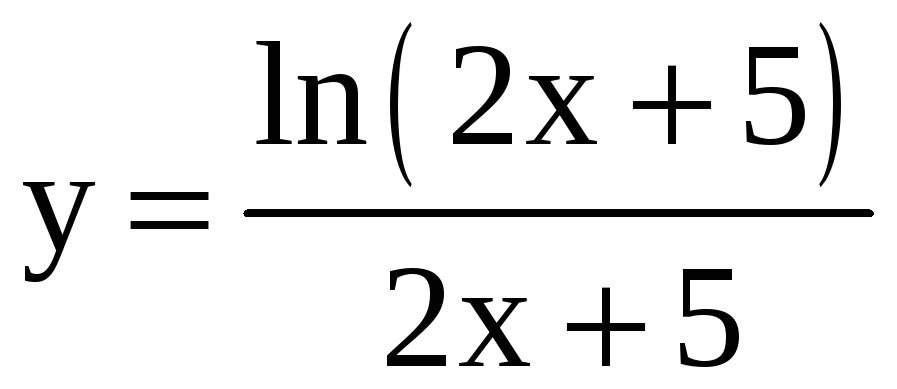 ; 26)
; 26)
![]() ;
;
14)
![]() ; 27)
; 27)
![]() ;
;
15)
![]() ; 28)
; 28)
![]() ;
;
16)
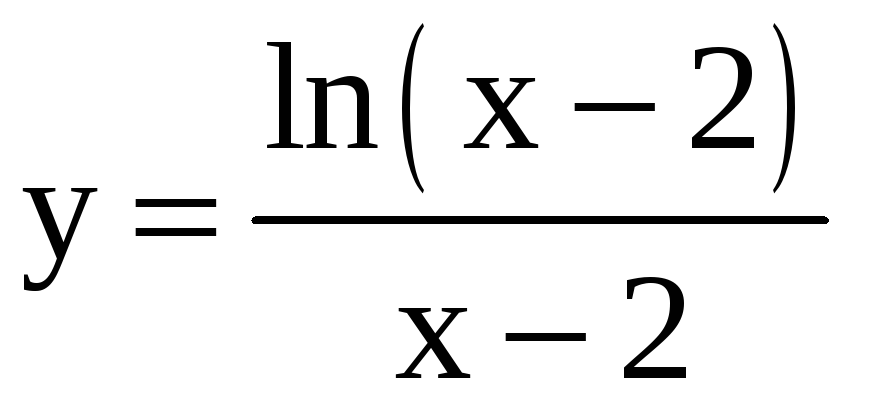 ; 29)
; 29)
![]() ;
;
17)
![]() ; 30)
; 30)
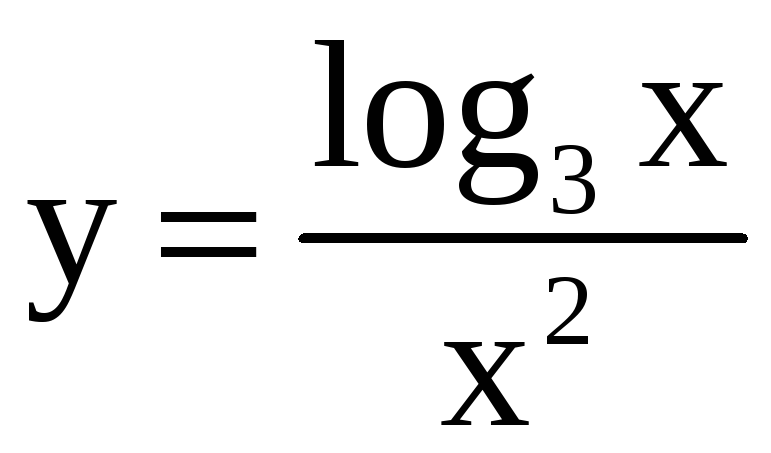 .
.
Задание 5.13
Найдите производные первого и второго порядков в точке
M(x0, y0) от функции, заданной неявно.
1)
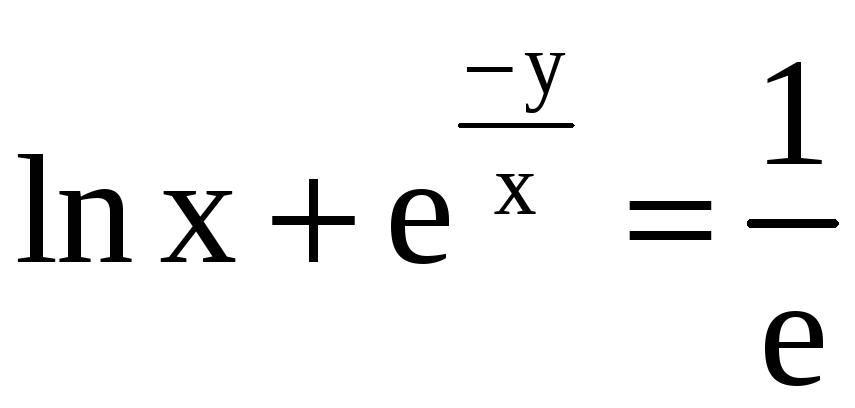 ,
M(1;
1); 5)
,
M(1;
1); 5)
![]() ,
M(1;
/4);
,
M(1;
/4);
2)
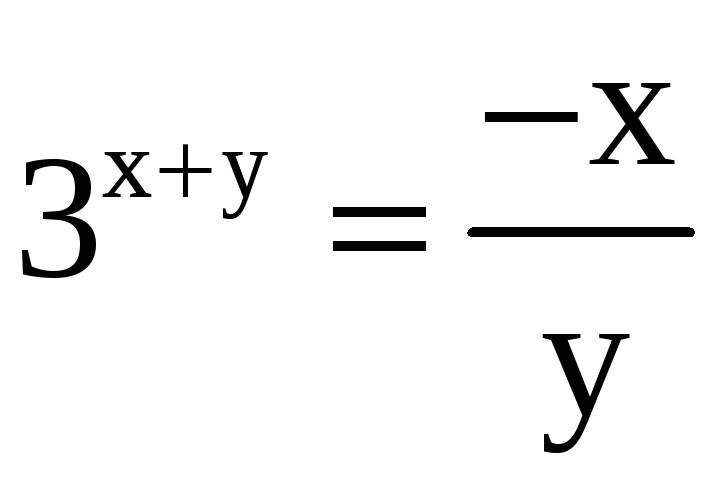 ,
M(1;
–1); 6)
,
M(1;
–1); 6)
![]() ,
M(0;
/4);
,
M(0;
/4);
3)
![]() ,
M(1;
1); 7)
,
M(1;
1); 7)
![]() ,
M(0;
/4);
,
M(0;
/4);
4)
![]() ,
M(0;
1); 8)
,
M(0;
1); 8)
![]() ,
M(1;
0);
,
M(1;
0);
9)
![]() ,
M(0;
1); 20)
,
M(0;
1); 20)
![]() ,
M(1;
1);
,
M(1;
1);
10)
![]() ,
M(2;
–1); 21)
,
M(2;
–1); 21)
![]() ,
M(0;
2);
,
M(0;
2);
11)
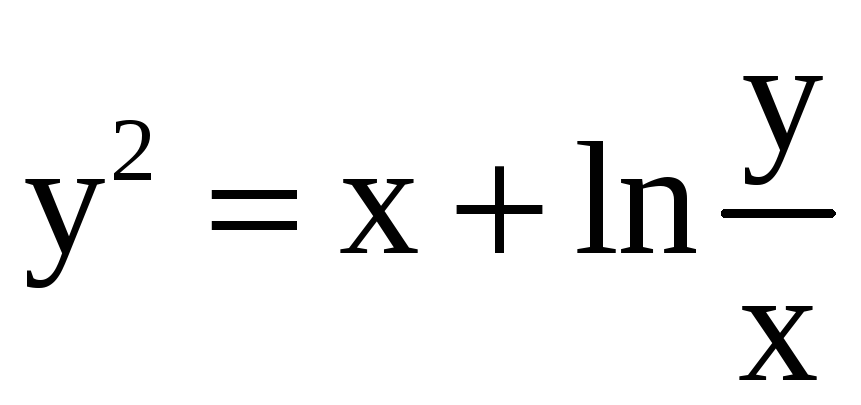 ,
M(1;
1); 22)
,
M(1;
1); 22)
![]() ,
M(2;1);
,
M(2;1);
12)
![]() ,
M(4/;
/4); 23)
,
M(4/;
/4); 23)
![]() ,
M(1;
2);
,
M(1;
2);
13)
![]() ,
M(–1;
0); 24)
,
M(–1;
0); 24)
![]() ,
M(0;
1);
,
M(0;
1);
14)
![]() ,
M(0;
/2); 25)
,
M(0;
/2); 25)
![]() ,
M(0;
/2);
,
M(0;
/2);
15)
![]() ,
M(0;0); 26)
,
M(0;0); 26)
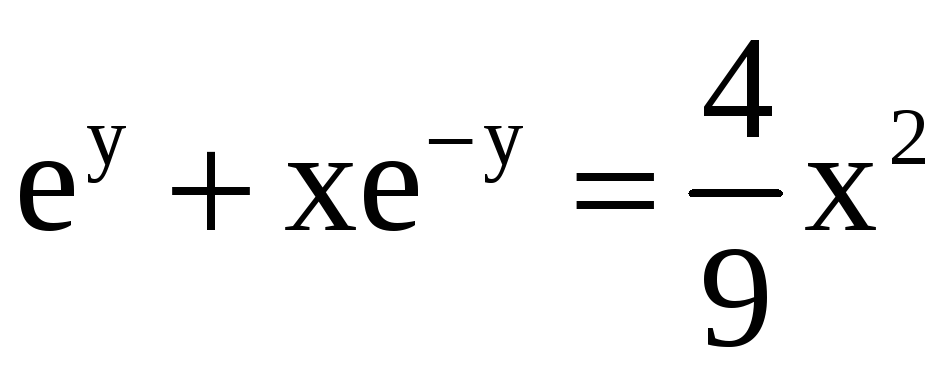 ,
M(3;
0);
,
M(3;
0);
16)
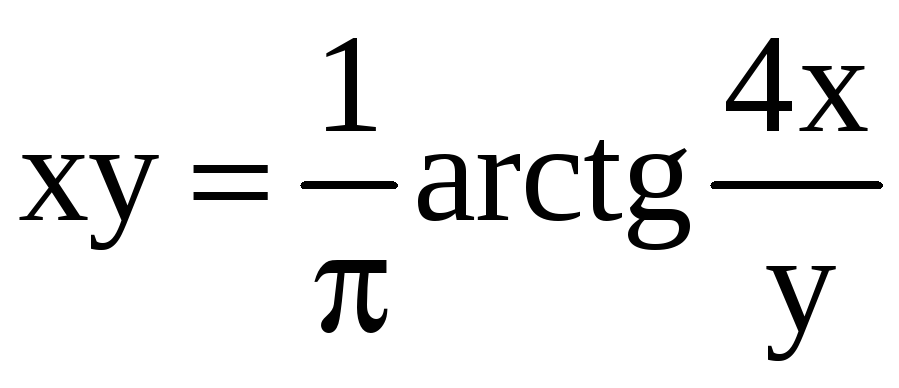 ,
M(1/4;1);
27)
,
M(1/4;1);
27)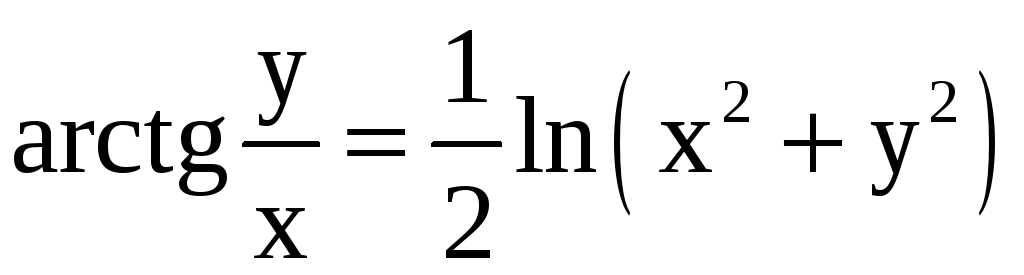 ,M(1;0);
,M(1;0);
17)
![]() ,
M(0;0); 28)
,
M(0;0); 28)
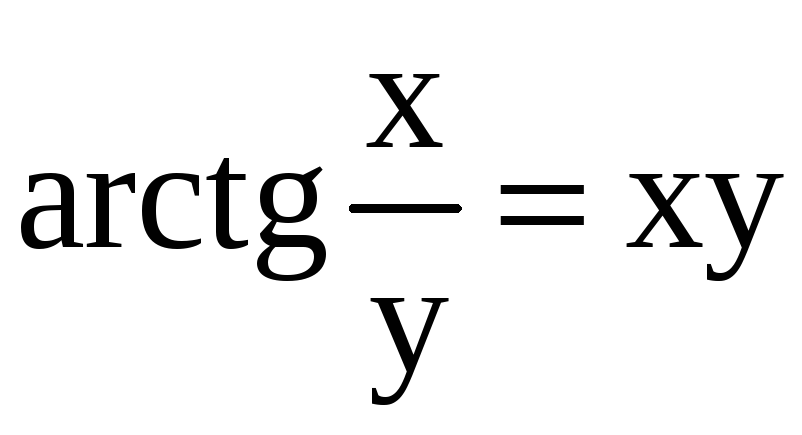 ,
M(0;1);
,
M(0;1);
18)
![]() ,
M(0;0);
29)
,
M(0;0);
29)
![]() ,
M(0;0);
,
M(0;0);
19)
![]() ,
M(0;1); 30)
,
M(0;1); 30)
![]() ,
M(0;1).
,
M(0;1).
Задание 5.14
Найдите производные 1-го и 2-го порядков от функций, заданных параметрически.
|
1) |
5) |
9) |
|
2) |
6) |
10) |
|
3) |
7) |
11) |
|
4) |
8) |
12) |
|
13) |
19) |
25) |
|
14) |
20) |
26) |
|
15) |
21) |
27) |
|
16) |
22) |
28) |
|
17) |
23) |
29) |
|
18) |
24) |
30) |
Задание 5.15
Найдите площадь треугольника, образованного прямой
![]() ,
касательной и нормалью, проведёнными
к графику заданной функции в точке с
заданной абсциссой x0
или в точке, соответствующей значению
параметра t0.
,
касательной и нормалью, проведёнными
к графику заданной функции в точке с
заданной абсциссой x0
или в точке, соответствующей значению
параметра t0.
1)
![]() ; 5)
; 5)
![]() ;
;
2)
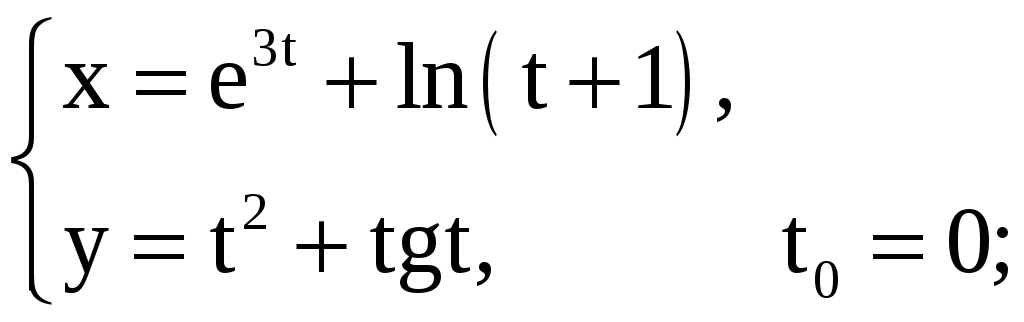 6)
6)
![]() ;
;
3)
![]() ; 7)
; 7)
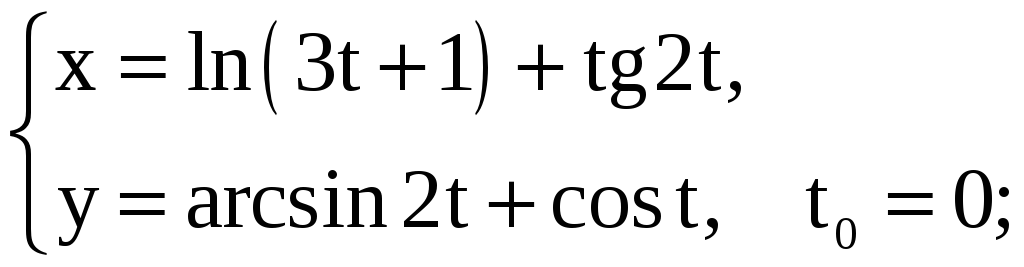
4)
![]() ; 8)
; 8)
![]() ;
;
9)
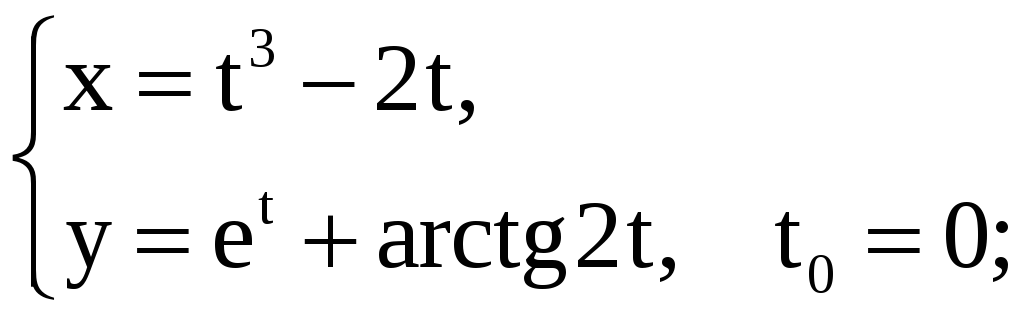 20)
20)
![]() ;
;
10)
![]() ;
21)
;
21)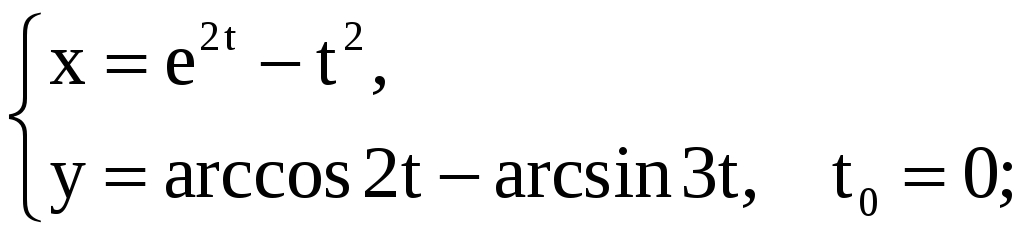
11)
![]() ; 22)
; 22)
![]() ;
;
12)
 23)
23) ![]() ;
;
13)
![]() ; 24)
; 24)
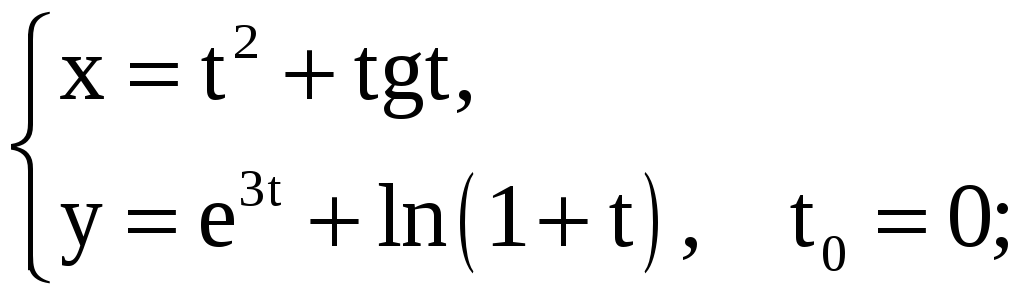
14)
![]() ; 25)
; 25)
![]() ;
;
15)
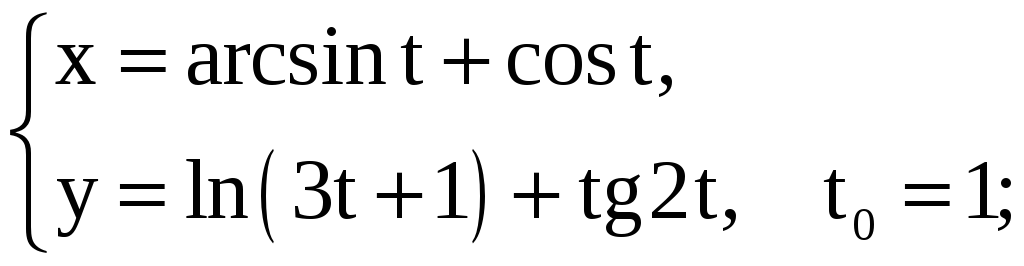 26)
26)
![]() ;
;
16)
![]() ; 27)
; 27)
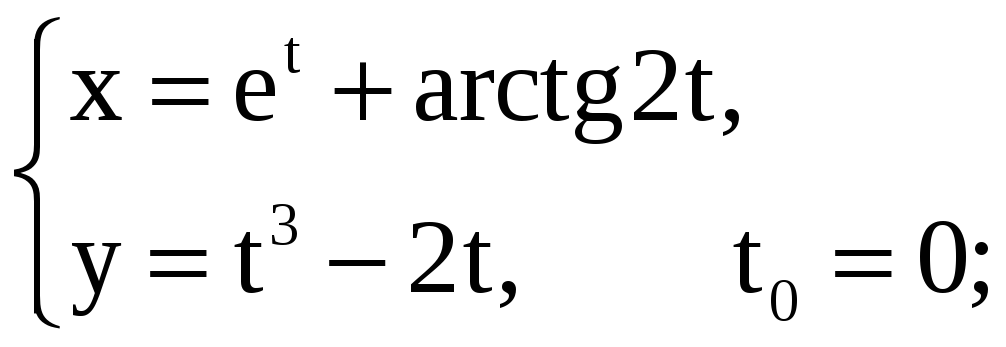
17)
![]() ; 28)
; 28)
![]() ;
;
18)
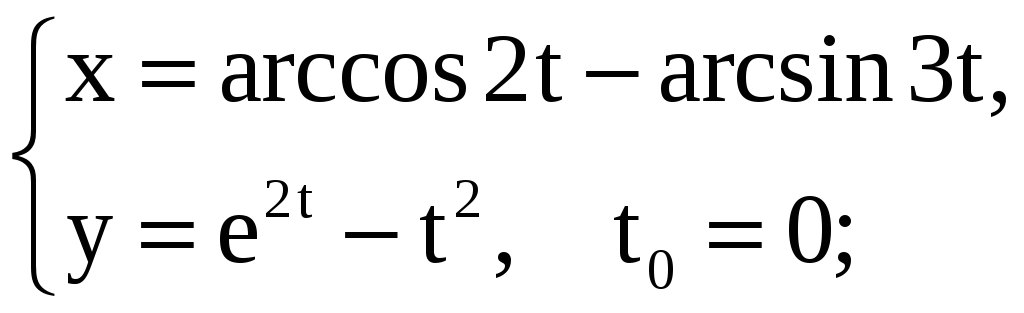 29)
29)
![]() ;
;
19)
![]() ; 30)
; 30)