Глава VII Дифференциальное исчисление функций одного переменного

п. 1 Определение производной

Определение 1. Пусть функция определена в некоторой окрестности точки . Тогда если существует предел отношения приращения функции к приращению аргумента при , то он называется производной функции в точке :

.

Геометрический смысл производной

Заметим, что в – угол наклона хорды , где , а б - угла наклона касательной, проведенной к графику функции . Если , то . Это значит, что . Таким образом, значение производной функции в точке равно тангенсу угла наклона касательной, проведенной к графику функции в точке с абсциссой .

Физический (механический) смысл производной

Пусть точка движется по закону . Вычислим среднюю скорость движения за момент времени : . Устремим , тогда .

Таким образом, значение производной перемещения в момент времени равно мгновенной скорости движения точки в данный момент времени.

Рассмотрим функцию .

Тогда .

Пример. Рассмотрим функцию .

Тогда .

Пример. Рассмотрим функцию .

Тогда

.

Пример. Рассмотрим функцию .

Найдем значение производной данной функции при .

Так как ,

, то производная этой функции в точке не существует. Более того,

функция является производной исходной функции при .

Определение 2. Пусть функция определена в некоторой окрестности точки , тогда называется дифференцируемой в этой точке, если приращение функции в данной точке представимо в виде:

, где и .

Теорема 1. Критерий дифференцируемости функции в точке

Для того, чтобы функция была дифференцируема в точке , необходимо и достаточно, чтобы в этой точке у нее существовала производная.

Доказательство:

Необходимость. Пусть дифференцируема в точке , тогда по определению ее приращение можно представить в виде: .

Найдем отношение приращения функции к приращению аргумента: . Перейдем к пределу: .

С другой стороны, этот предел равен , т.е. .

Достаточность. Пусть существует . Тогда по определению производной: . Это значит, что: . Умножив последнее равенство на x, получим: .

Полагая, , мы получили определение дифференцируемости. ■

Замечание. Процесс нахождения производной функции в точке называют дифференцированием.

Замечание. Производную называют правой производной функции в точке , а производную - левой производной.

Таким образом, , причем .

Теорема 2. Если функция дифференцируема в точке , то она непрерывна в этой точке.

Доказательство:

Пусть функция дифференцируема в точке . Тогда по определению . Найдем . Значит, является бесконечно малой функцией. Следовательно, функция непрерывна в точке . ■

Замечание. Обратное утверждение неверно. Например, функция непрерывна в точке , но не дифференцируема в этой точке.

Определение 3. Говорят, что функция дифференцируема на отрезке , если она дифференцируема в каждой внутренней точке этого отрезка.

п. 2 Правила дифференцирования

Теорема 1. Пусть и - дифференцируемые функции в точке . Тогда:

1. ;

2. ;

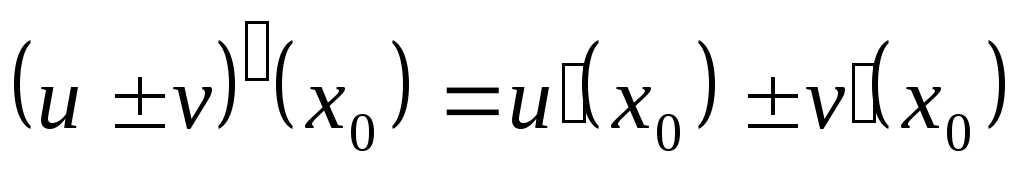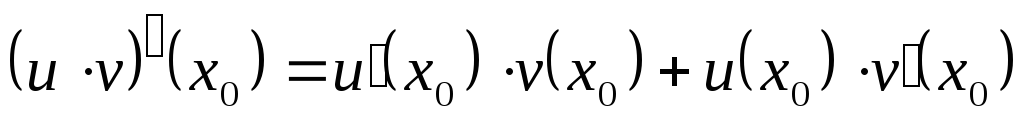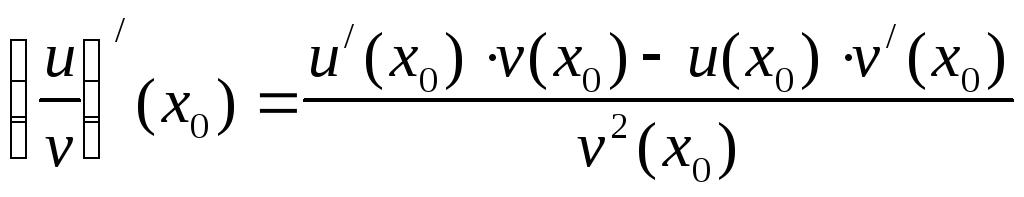3. , причем в некоторой окрестности точки .

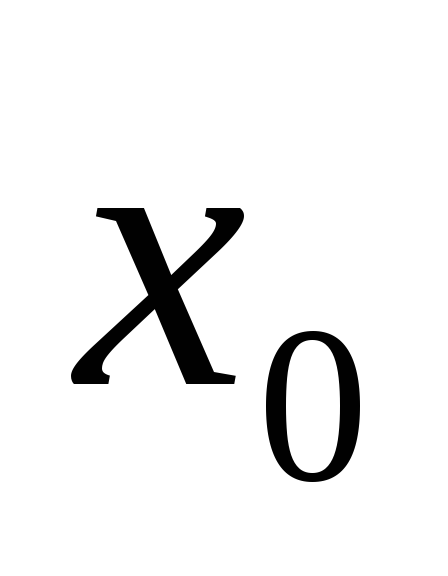Доказательство:

Докажем третье утверждение данной теоремы. Для этого рассмотрим приращение:

_.

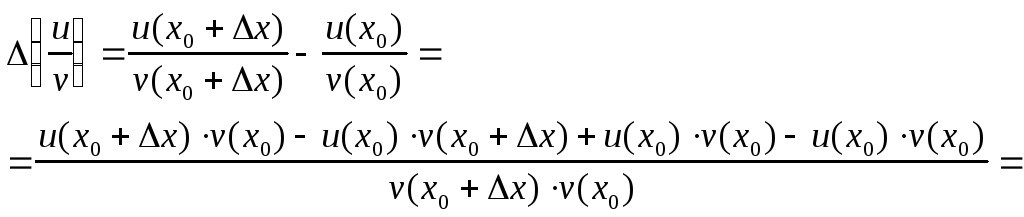
Найдем предел:

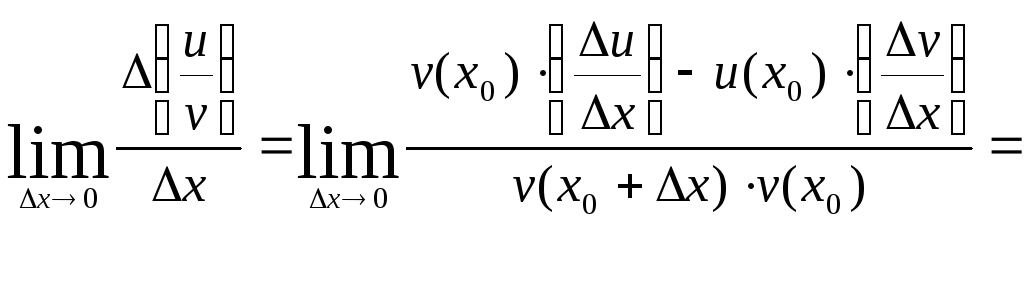
. Таким образом, . ■

Теорема 2.Пусть функция дифференцируема в точке и биективна (т.е. наша функция имеет обратную функцию). Тогда обратная функция дифференцируема в точке , причем .

Доказательство:

Рассмотрим приращение функции , т.е. . Тогда .

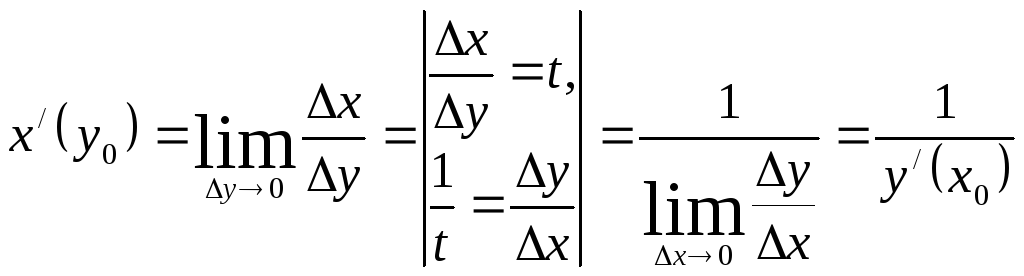Так как функция дифференцируема в точке , то она непрерывна в этой точке, следовательно, малому приращению аргумента соответствует малое приращение функции . ■

Замечание. Геометрический смысл производной обратной функции (рисунок)

Так как , где - угол наклона касательной, проведенной к графику функции в точке с абсциссой , то .

Замечание. Если растет быстрее в раз, то отстает на раз.

Теорема 3. Пусть функция дифференцируема в некоторой точке , а функция дифференцируема в точке , которая является образом точки . Тогда функция дифференцируема в точке , причем .

Доказательство:

По условию функция дифференцируема в точке , т.е. . Тогда, используя дифференцируемость функции в точке , получим . Подставим в : .

Найдем предел . ■

Определение 1. Пусть . Говорят, что линия на плоскости задана параметрически, если ее точки имеют координаты . Таким образом, параметрическое задание данной линии равносильно ее явному заданию .

Теорема 4. Пусть функции дифференцируемы в точке , тогда функция дифференцируема в точке , причем .

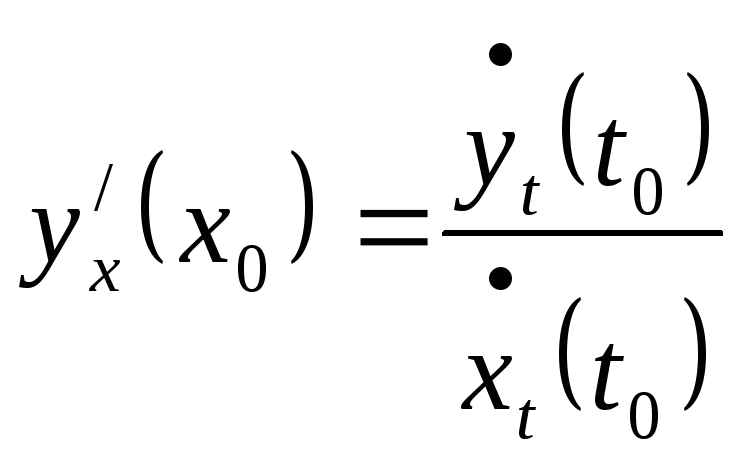Доказательство:

Рассмотрим ,

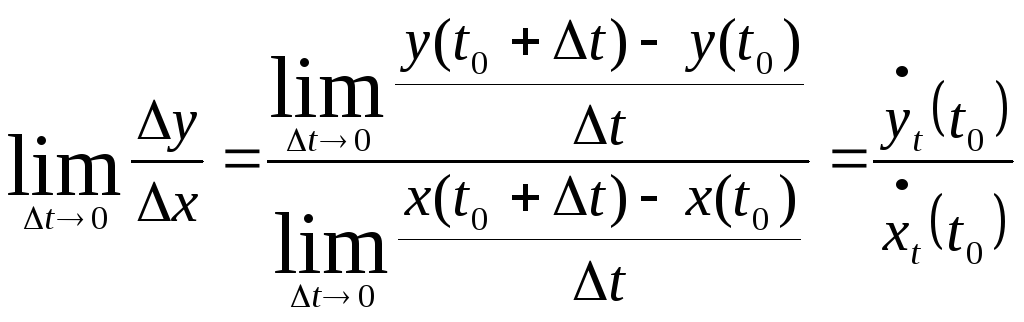. По условию функция дифференцируема в точке , следовательно, непрерывна в этой точке, значит, бесконечно малому соответствует бесконечно малое .

Таким образом, . ■
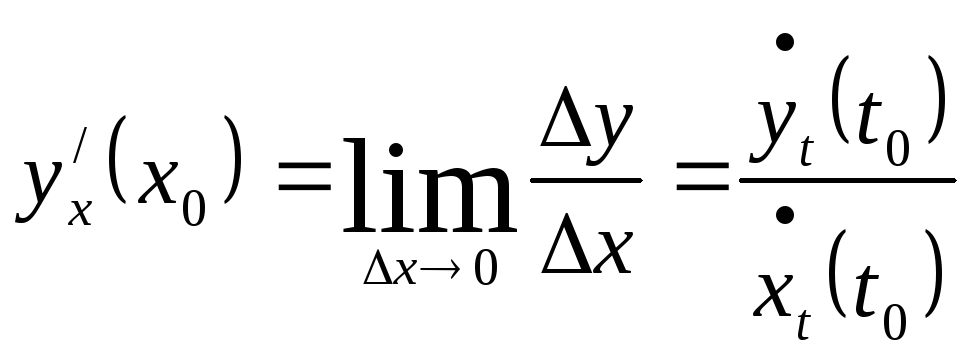