
Геометрический смысл теоремы Ферма
Если
функция
![]() на отрезке
на отрезке
![]() имеет локальный экстремум, то касательная,
проведенная к графику функции в этой
точке, параллельна оси
имеет локальный экстремум, то касательная,
проведенная к графику функции в этой
точке, параллельна оси
![]() .
.
Теорема 2. Теорема Ролля
Пусть
![]() непрерывна на отрезке
непрерывна на отрезке
![]() и дифференцируема на интервале
и дифференцируема на интервале
![]() ,
причем
,
причем
![]() .Тогда
найдется точка
.Тогда
найдется точка
![]() .
.
Доказательство:
Так
как функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() ,
то по теореме Вейерштрасса она достигает
своих наибольшего и наименьшего значений
(ТВГ, ТНГ).
,
то по теореме Вейерштрасса она достигает
своих наибольшего и наименьшего значений
(ТВГ, ТНГ).
Пусть
![]() ,
а
,
а
![]() .
Тогда возможны два случая:
.
Тогда возможны два случая:
1.
Если
![]() ,
то
,
то
![]() .
Тогда
.
Тогда
![]() .
.
2.
Если
![]() ,
то пусть
,
то пусть
![]() .
Это значит, что на интервале
.
Это значит, что на интервале
![]() ,
по крайней мере, в одной точке
,
по крайней мере, в одной точке
![]() функция
функция
![]() будет иметь экстремум, а по теореме
Ферма
будет иметь экстремум, а по теореме
Ферма
![]() .
■
.
■
Замечание. Все условия данной теоремы существенны. (рисунки – 3 шт.).
Теорема 2. Теорема Лагранжа
Пусть
функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() и дифференцируема на интервале
и дифференцируема на интервале
![]() ,
тогда найдется точка
,
тогда найдется точка
![]() .
.
Доказательство:
Введем
вспомогательную функцию
![]() так, чтобы функция
так, чтобы функция
![]() удовлетворяла теореме Ролля, т.е.
удовлетворяла теореме Ролля, т.е.
![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
Тогда
![]() ,
,
![]() ,
,
![]() .
Таким образом,
.
Таким образом,
![]() ■
■
Замечание. Геометрический смысл теоремы:
точка
,
в которой касательная к графику функции
имеет такой же наклон, как и хорда,
соединяющая точки
![]() и
и
![]() .
(Рисунок)
.
(Рисунок)
![]() .
.
Замечание. Теорема Лагранжа является обобщением теоремы Ролля.
Следствие 1. Формула конечного приращения
Если
![]() то
то
![]()
![]() где
где
![]() ,
или
,
или
![]() .
.
Следствие 2. Критерий монотонности
Для
того, чтобы функция
![]() ,
непрерывная на отрезке
,
непрерывная на отрезке
![]() и дифференцируемая на интервале
и дифференцируемая на интервале
![]() ,
была неубывающей (невозрастающей),
необходимо и достаточно, чтобы
,
была неубывающей (невозрастающей),
необходимо и достаточно, чтобы
![]() .
.
Доказательство:
Необходимость.
Пусть функция
![]() не убывает на отрезке
не убывает на отрезке
![]() .
Тогда, по определению, имеем
.
Тогда, по определению, имеем
![]() .
Возьмем любой
.
Возьмем любой
![]() и придадим ему положительное приращение
и придадим ему положительное приращение
![]() .
Получим
.
Получим
![]() .
.
Достаточность.
Пусть
![]() .
Возьмем точки
.
Возьмем точки
![]() такие, что
такие, что
![]() и применим теорему Лагранжа:
и применим теорему Лагранжа:
![]() ,
где
,
где
![]() .
Тогда
.
Тогда
![]() или
или
![]() .
Таким образом, получили определение
неубывающей функции. ■
.
Таким образом, получили определение
неубывающей функции. ■
Теорема 3. Теорема Коши
Пусть
функции
![]() и
и
![]() непрерывны на отрезке
непрерывны на отрезке
![]() и дифференцируемы на интервале
и дифференцируемы на интервале
![]() ,
причем
,
причем
![]() .
Тогда
.
Тогда
![]() такая, что
такая, что
![]() .
.
Доказательство:
Докажем
сначала, что
![]() .
Функция
.
Функция
![]() удовлетворяет условиям теоремы Лагранжа,
значит, что
удовлетворяет условиям теоремы Лагранжа,
значит, что
![]() .
Отсюда
.
Отсюда
![]() .
.
Введем
вспомогательную функцию
![]() так, чтобы она удовлетворяла условиям
теоремы Ролля.
так, чтобы она удовлетворяла условиям
теоремы Ролля.
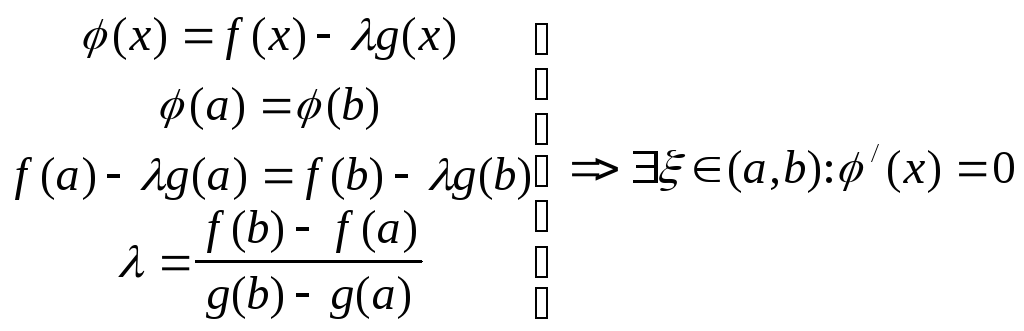 .
.
Тогда
![]() .
Отсюда
.
Отсюда
![]() .
.
Таким образом,
![]() или
или
![]() .
■
.
■
Замечание. Теорема Коши является наиболее общей теоремой, т.е. теорема Ролля и Лагранжа являются следствиями из теоремы Коши.
Теорема 4. Теорема Лопиталя
Пусть
функции
![]() и
и
![]() непрерывны и дифференцируемы в некоторой
проколотой окрестности
непрерывны и дифференцируемы в некоторой
проколотой окрестности
![]() точки
точки
![]() ,
причем
,
причем
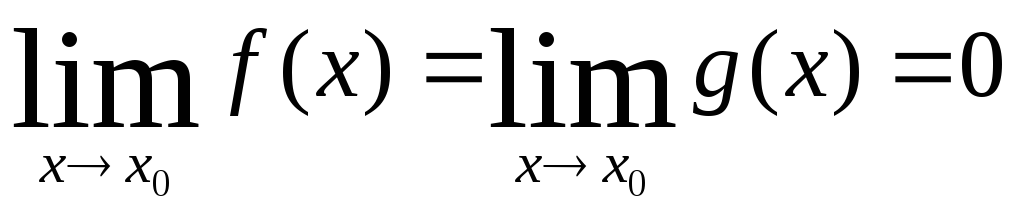 ,
,
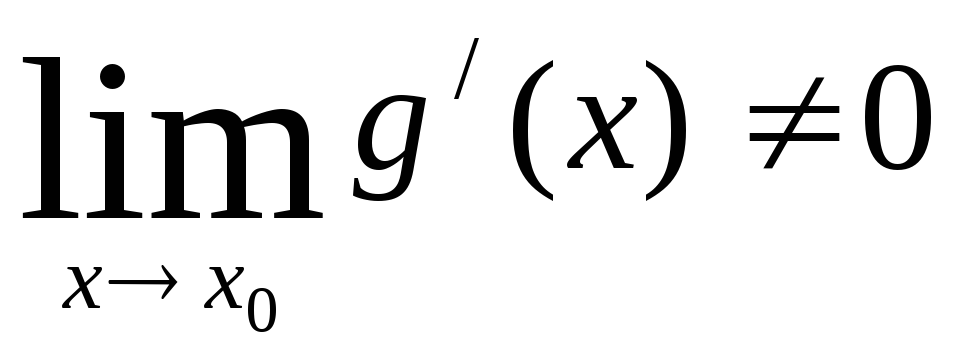 и
и
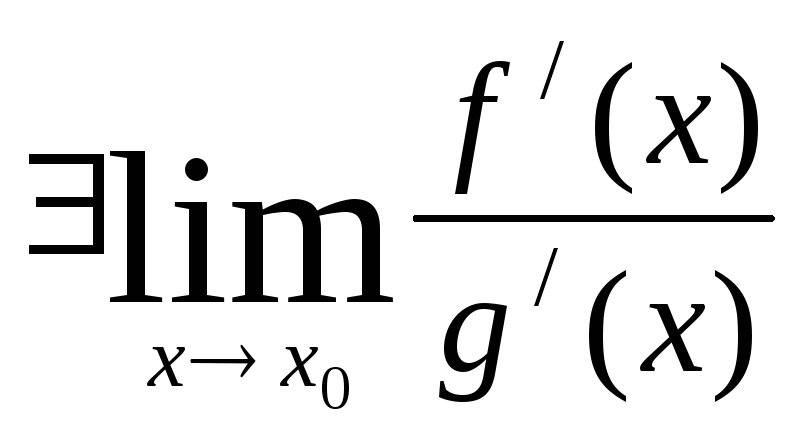 .
Тогда
.
Тогда
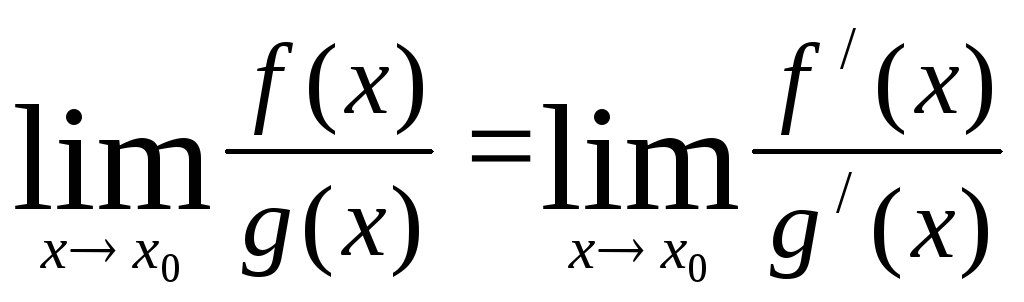 .
.
Доказательство:
Рассмотрим
окрестность
![]() .
(Рисунок) Выберем последовательность
.
(Рисунок) Выберем последовательность
![]() .
Тогда, начиная с некоторого номера N,
члены последовательности попадают в
эту окрестность. Тогда, так как
.
Тогда, начиная с некоторого номера N,
члены последовательности попадают в
эту окрестность. Тогда, так как
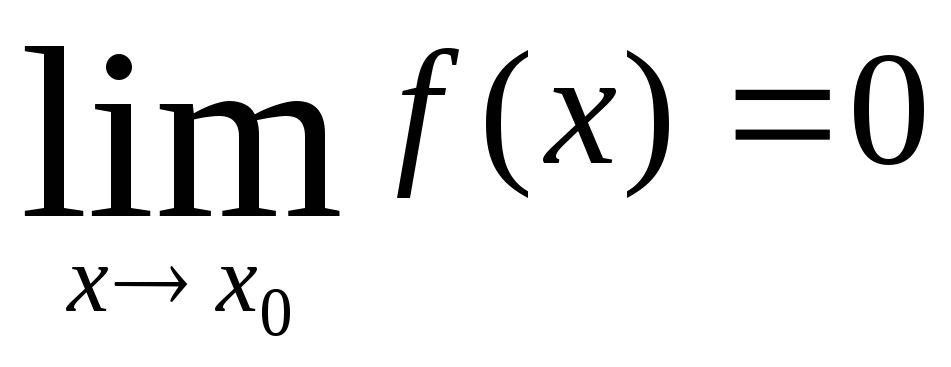 и
и
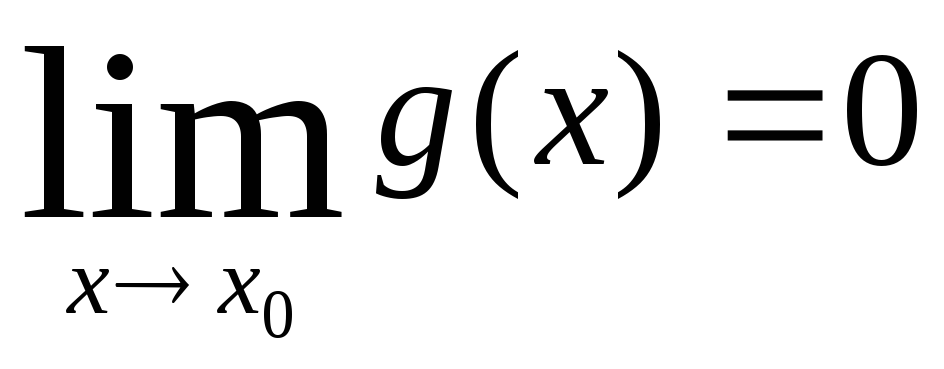 ,
то функции
,
то функции
![]() и
и
![]() в точке
в точке
![]() имеют устранимый разрыв. Доопределим
эти функции до непрерывности:
имеют устранимый разрыв. Доопределим
эти функции до непрерывности:
![]() ,
,
![]() .
Тогда на отрезке
.
Тогда на отрезке
![]() данные функции непрерывны и дифференцируемы
на интервале
данные функции непрерывны и дифференцируемы
на интервале
![]() .
Таким образом, выполняются все условия
теоремы Коши. Это значит, что
.
Таким образом, выполняются все условия
теоремы Коши. Это значит, что
![]() ,
где
,
где
![]() ,
или
,
или
![]() .
.
Перейдем
к пределу при
![]() :
:
![]() ,
,
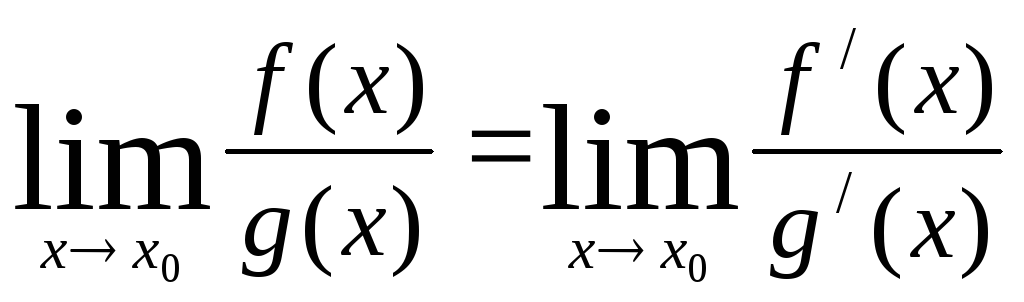 .
■
.
■
Замечание.
Если
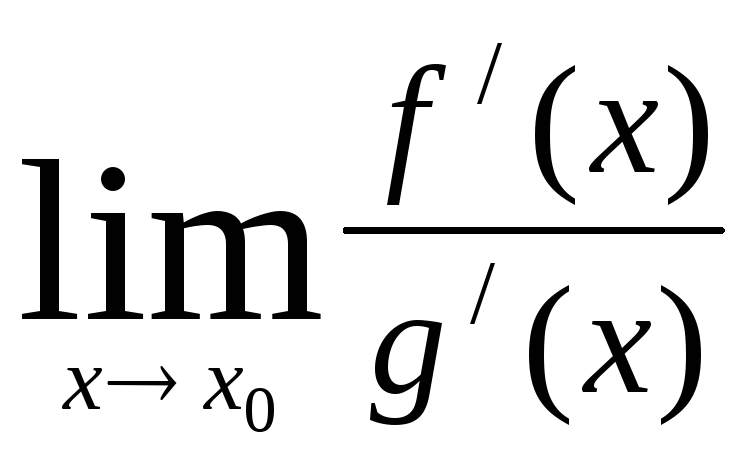 не существует, то из этого не следует,
что не существует
не существует, то из этого не следует,
что не существует
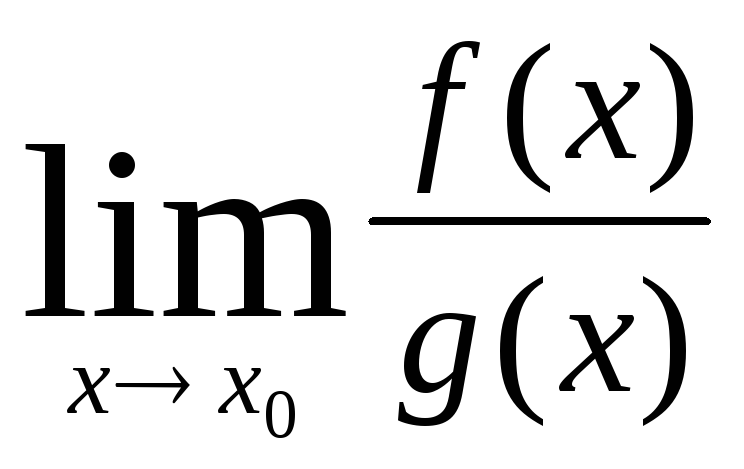 .
.
Пример.
Вычислим
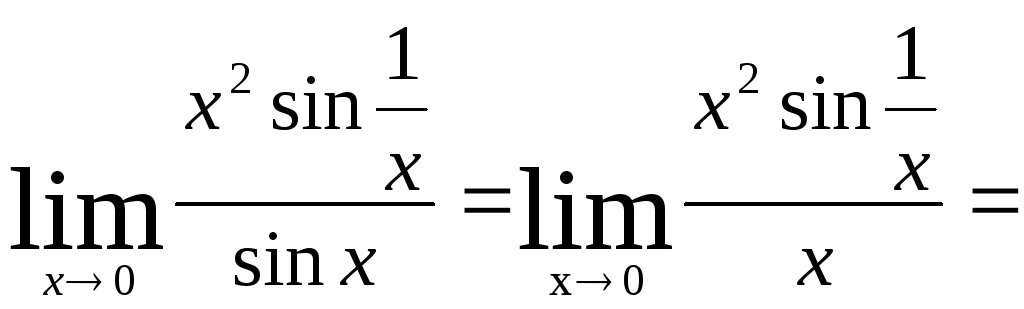
![]() ,
но
,
но
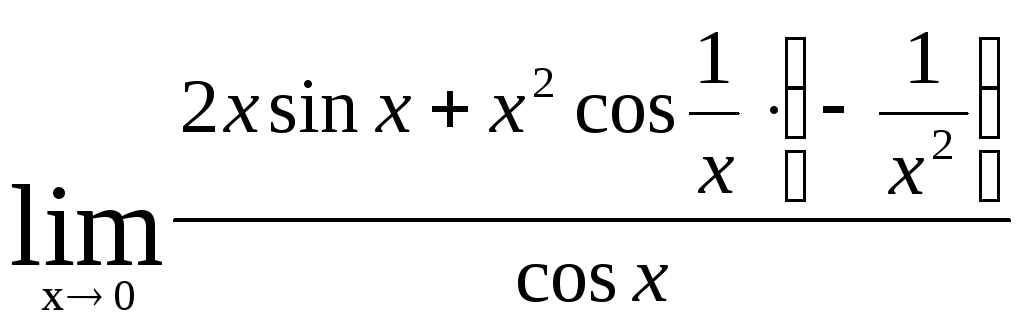 не существует.
не существует.
Пример.
Вычислим
![]() .
Применяя правило Лопиталя, получим
.
Применяя правило Лопиталя, получим
![]()
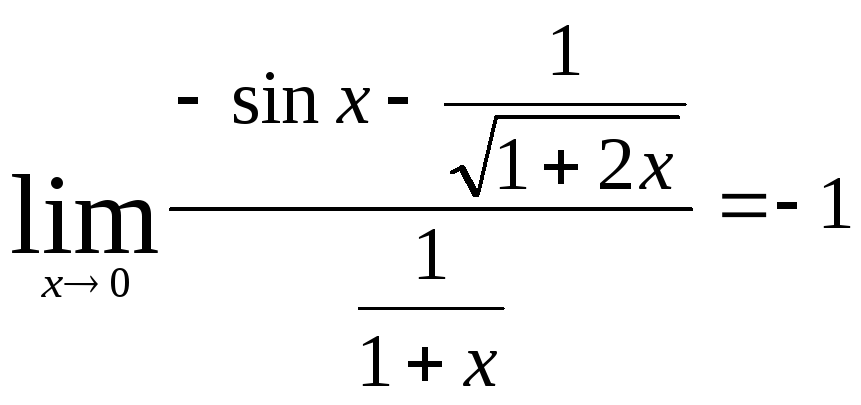 .
.
Замечание.
Теорема Лопиталя сформулирована для
неопределенности типа
![]() и имеет место для неопределенностей
типа
и имеет место для неопределенностей
типа
![]()
Пример.
Вычислим
![]() .
Для этого прологарифмируем функцию
.
Для этого прологарифмируем функцию
![]() .
Тогда
.
Тогда
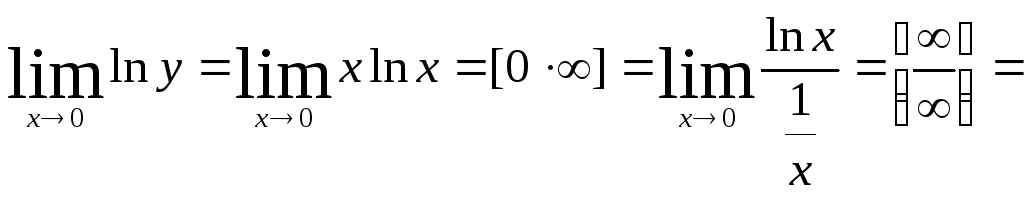
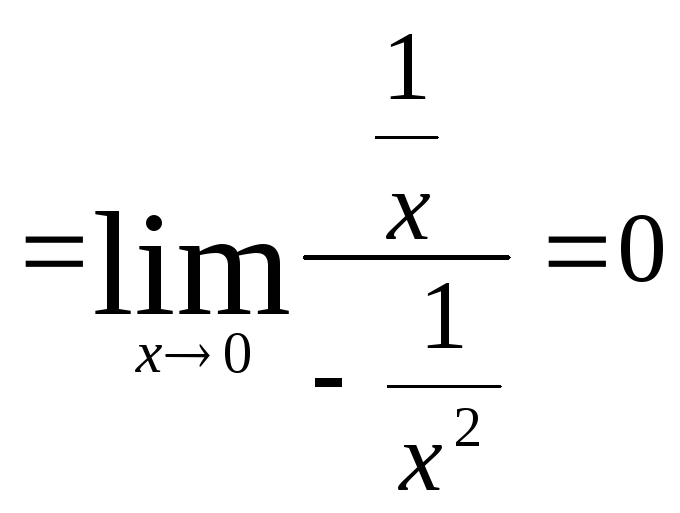 .
Следовательно,
.
Следовательно,
![]() .
.
п. 7 Формула Тейлора
Можно заметить,
что чем больше производных совпадают
у двух функций в некоторой точке, тем
лучше эти функции аппроксимируют
(приближают) друг друга в окрестности
этой точки. Нас будет интересовать
приближение функции в окрестности одной
точки с помощью многочленов. Рассмотрим
многочлен степени
![]() :
:
![]() .
Заметим, что
.
Заметим, что
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
Аналогично получим
.
Аналогично получим
![]() ,
,
![]() .
.
Определение
1. Функция
![]() называется гладкой
порядка
называется гладкой
порядка
![]() в точке
в точке
![]() на интервале
на интервале
![]() ,
если она имеет все производные порядка
,
если она имеет все производные порядка
![]() включительно, причем эти производные
являются непрерывными функциями на
отрезке
включительно, причем эти производные
являются непрерывными функциями на
отрезке
![]() .
Этот факт обозначается
.
Этот факт обозначается
![]() .
.
Определение
2. Выражение
вида
![]()
![]()
![]() называется
формулой
Тейлора для
функции
называется
формулой
Тейлора для
функции
![]() в окрестности точки
в окрестности точки
![]() .
.
Теорема
1. Если функция
![]() является гладкой порядка
является гладкой порядка
![]() в некоторой окрестности точки
в некоторой окрестности точки
![]() ,
то имеет место формула Тейлора для
данной функции
,
то имеет место формула Тейлора для
данной функции
![]() .
.
Доказательство:
Пусть
имеет место формула Тейлора для функции
![]() :
:
![]() ,
причем
,
причем
![]() ,
,
![]() ,
,
![]() .
Обозначим
.
Обозначим
![]() .
.
Используя
правило Лопиталя, покажем, что
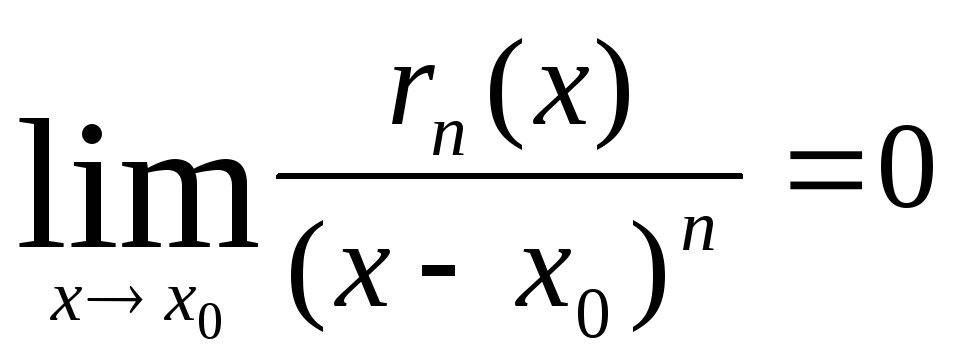 .
Так как
.
Так как
![]()
![]() ,
…,
,
…,
![]() ,
,![]() ,
,
тогда
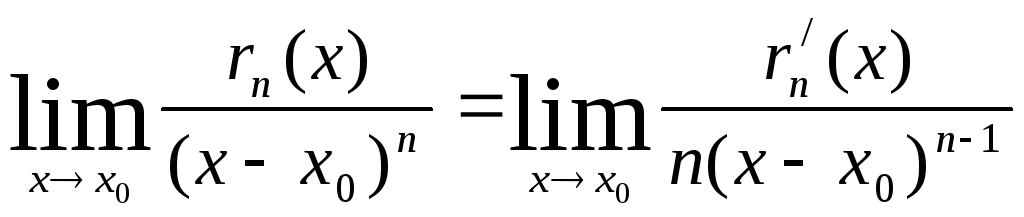 =
=
=…=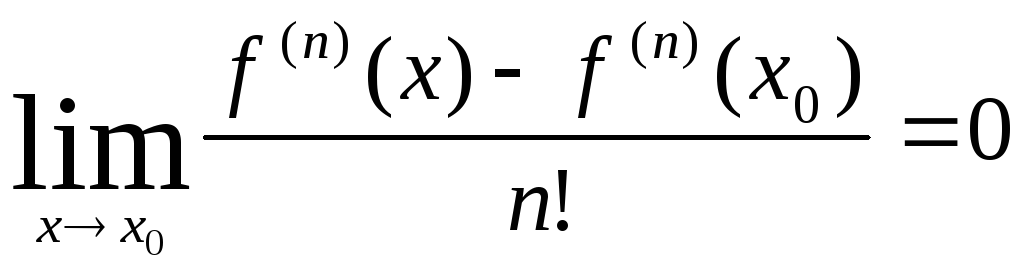 .
■
.
■
Замечание.
В формуле
Тейлора первое слагаемое называют
главной
частью
функции, а второе – остаточный
член функции
![]() .
.
Если
![]() ,
то формулу Тейлора
,
то формулу Тейлора
![]() для функции
для функции
![]() называют формулой
Маклорена.
называют формулой
Маклорена.
Остаточный
член в виде
![]() называют остаточным членом в форме
Пеано.
называют остаточным членом в форме
Пеано.
Формула
Тейлора используется для того, чтобы
приблизить функцию многочленом
![]()
![]() -й
степени в некоторой окрестности точки
-й
степени в некоторой окрестности точки
![]() :
:
![]()
Пример.
Разложим
многочлен
![]() по степеням
по степеням
![]() .
Для этого найдем коэффициенты разложения:
.
Для этого найдем коэффициенты разложения:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Тогда
.
Тогда
![]() .
.
Теорема 2. О единственности разложения функции по формуле Тейлора
Если
функция
![]() в некоторой окрестности точки
в некоторой окрестности точки
![]() имеет разложение по формуле Тейлора,
то это разложение единственно.
имеет разложение по формуле Тейлора,
то это разложение единственно.
Доказательство:
![]() .
Пусть функция
.
Пусть функция
![]() имеет два разложения:
имеет два разложения:
![]() ,
,
![]() .
.
Вычтем одно из другого и получим:
![]() .
.
Пусть
![]() ,
тогда
,
тогда
![]() .
Разделим полученное равенство
.
Разделим полученное равенство
![]() на
на
![]() .
Получим
.
Получим
![]()
![]() .
Тогда при
.
Тогда при
![]() получим
получим
![]() .
Рассуждая аналогично, получим
.
Рассуждая аналогично, получим
![]() .
Следовательно,
.
Следовательно,
![]() .
Таким образом, разложения совпадают.
■
.
Таким образом, разложения совпадают.
■
Замечание.
Обратное
утверждение, вообще говоря, неверно,
т.е. можно найти такие две функции,
которые будут иметь одинаковые разложения
по формуле Тейлора в некоторой окрестности
точки
![]() .
.
Разложение основных элементарных функций по формуле Маклорена
-
Функция
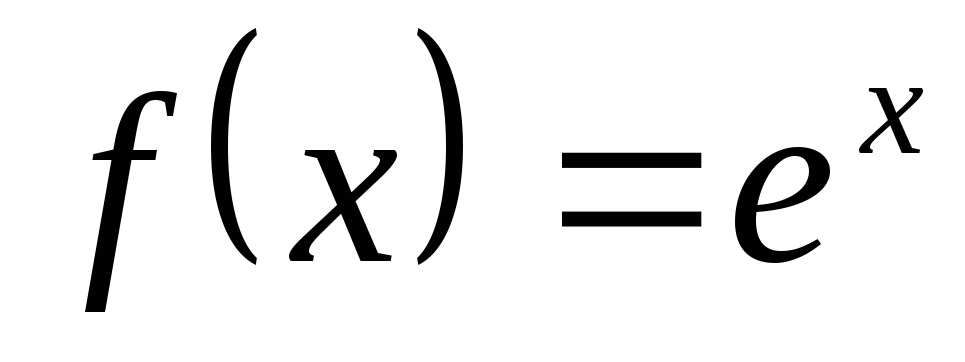 в окрестности точки
в окрестности точки
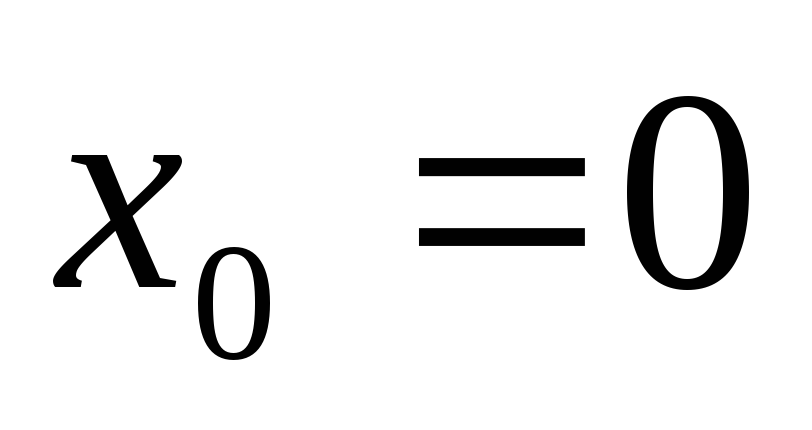 имеет разложение
имеет разложение
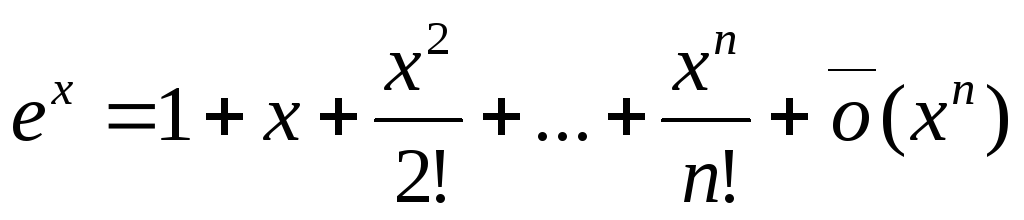 ,
так как
,
так как
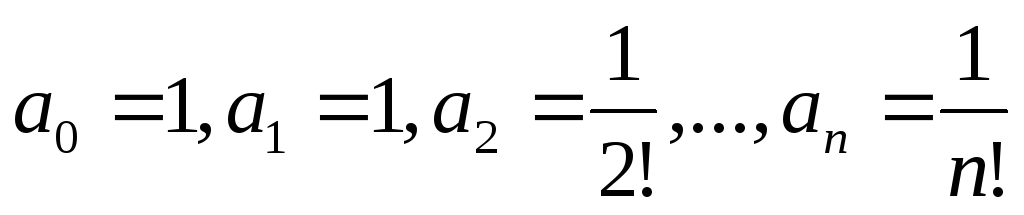 .
Данное разложение позволяет вычислить
.
Данное разложение позволяет вычислить
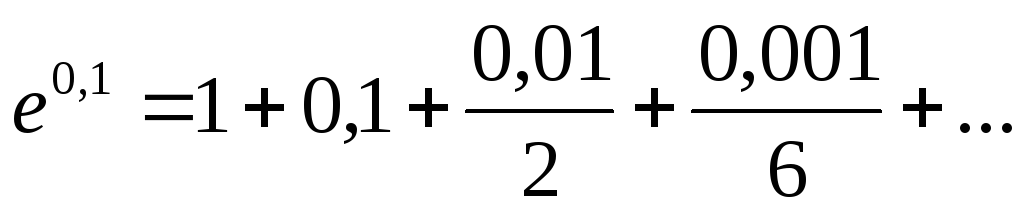 .
. -
Функция
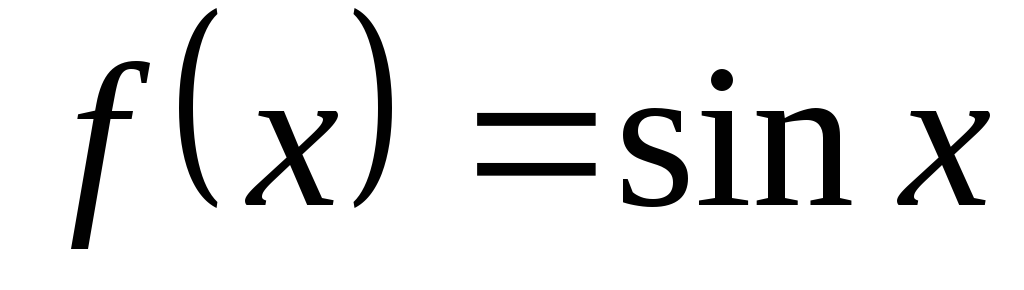 в окрестности точки
в окрестности точки
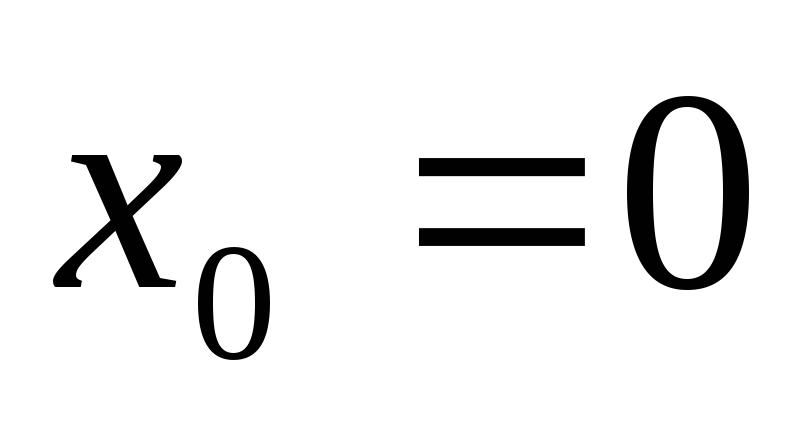 имеет разложение
имеет разложение
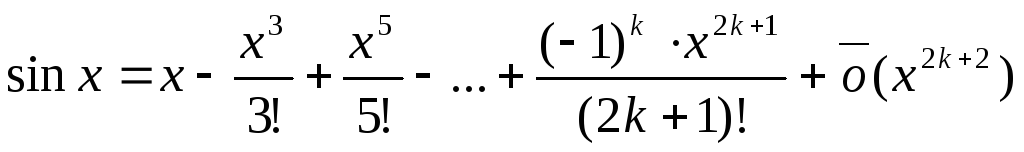 ,
так как
,
так как
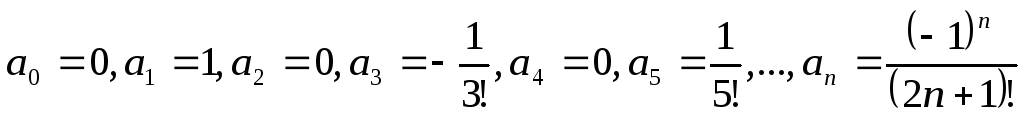 .
.
Аналогично имеют место следующие разложения:
-
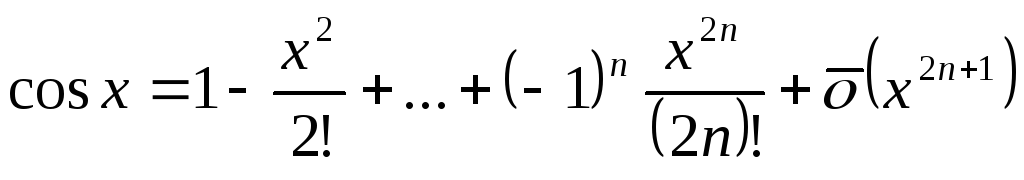 ;
; -
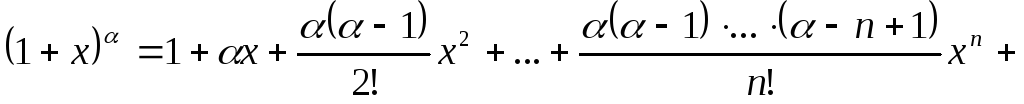
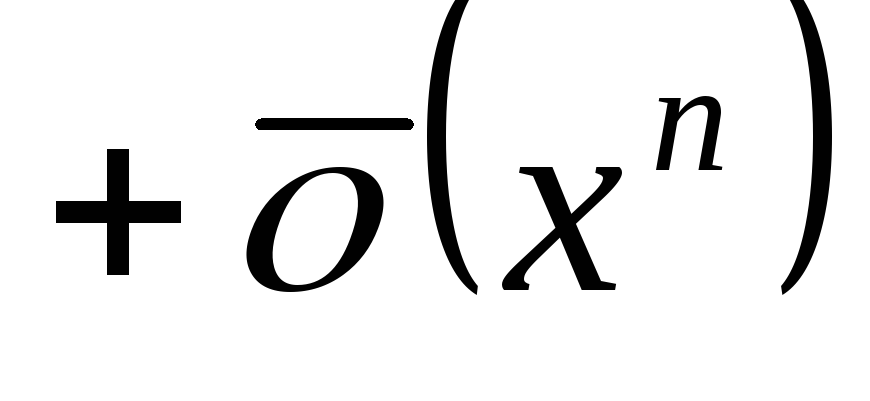 ;
; -
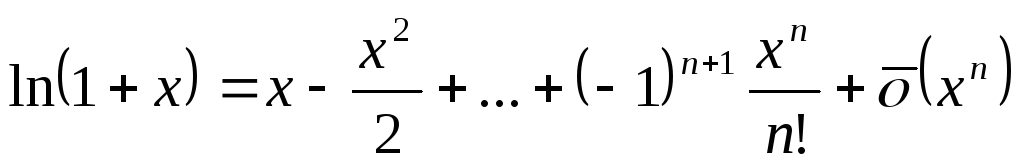 .
.
п. 8 Исследование функции и построение графиков
Определение
1. Точка
![]() ,
в которой производная
,
в которой производная
![]() равна нулю или не существует, называется
критической
точкой функции
равна нулю или не существует, называется
критической
точкой функции
![]() .
.
Пример.
Рассмотрим
функцию
![]() .
Произ-
.
Произ-
водная
![]() функции не существует в точке
функции не существует в точке
![]() .
Следовательно,
.
Следовательно,
![]() является критической точкой данной
функции. (рисунок)
является критической точкой данной
функции. (рисунок)
Пусть
![]() является критической точкой функции
является критической точкой функции
![]() ,
дифференцируемой в некоторой окрестности
этой точки (кроме, может быть, самой
точки
,
дифференцируемой в некоторой окрестности
этой точки (кроме, может быть, самой
точки
![]() )
и непрерывной в ней. Тогда, если производная
меняет знак при переходе через точку
)
и непрерывной в ней. Тогда, если производная
меняет знак при переходе через точку
![]() ,
то в этой точке функция
,
то в этой точке функция
![]() имеет экстремум, а именно, если
имеет экстремум, а именно, если
![]() меняет знак с “+” на “-”, то
меняет знак с “+” на “-”, то
![]() - точка максимума; если с “-” на “+”,
то
- точка максимума; если с “-” на “+”,
то
![]() - точка минимума. Если производная знак
не меняет, то экстремума в точке
- точка минимума. Если производная знак
не меняет, то экстремума в точке
![]() нет. Таким образом, например, если
нет. Таким образом, например, если
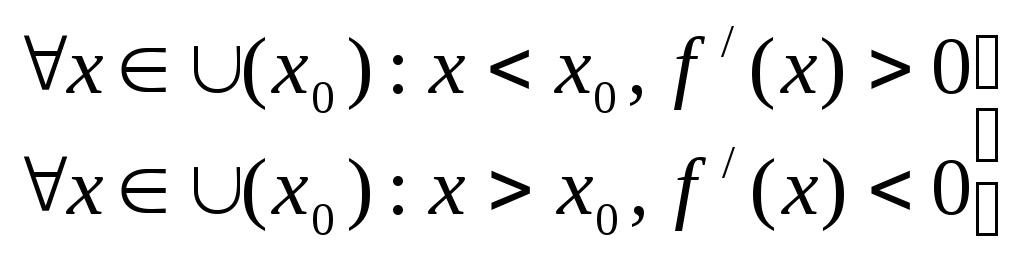 ,
то
,
то
![]() - точка максимума функции
- точка максимума функции
![]() .
Применим теорему Лагранжа. Так как
.
Применим теорему Лагранжа. Так как
![]() ,
то неравенство
,
то неравенство
![]() имеет место для всех
имеет место для всех
![]() из левой полуокрестности точки
из левой полуокрестности точки
![]() .
Так как
.
Так как
![]() ,
то неравенство
,
то неравенство
![]() имеет место для всех
имеет место для всех
![]() из правой полуокрестности точки
из правой полуокрестности точки
![]() .
Таким образом, получили определение
точки максимума функции
.
Таким образом, получили определение
точки максимума функции
![]() :
:
![]()
Аналогично
рассуждая, получим, что если
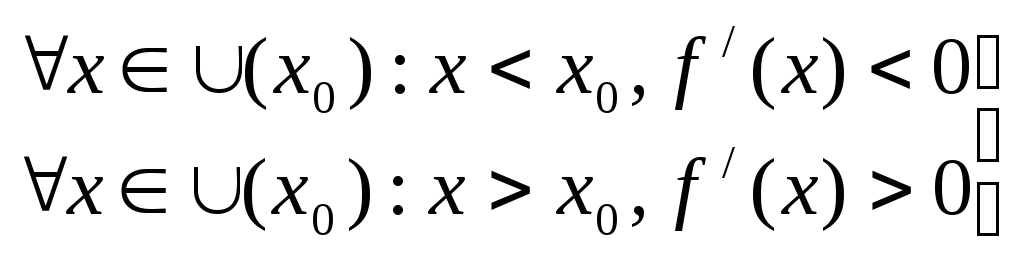 ,
то
,
то
![]() - точка минимума функции
- точка минимума функции
![]() .
.
Теорема
1. Если
![]() является критической точкой функции
является критической точкой функции
![]() и
и
![]() то:
то:
-
если
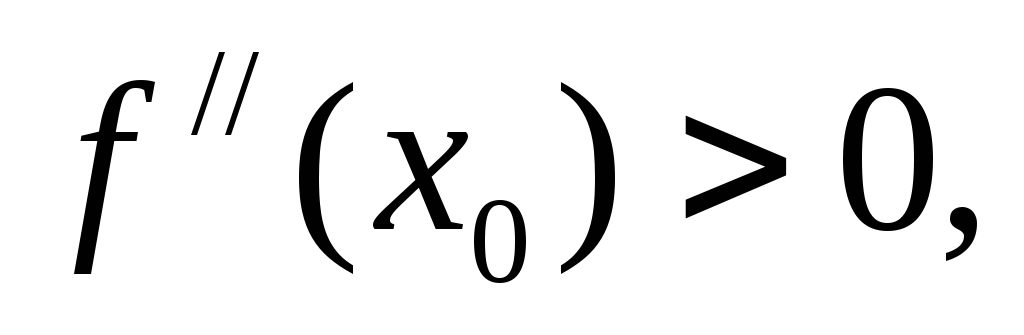 то
то
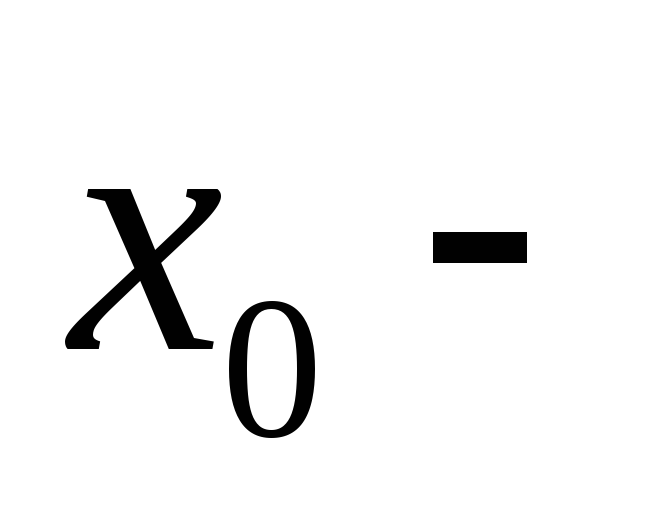 точка
минимума;
точка
минимума; -
если
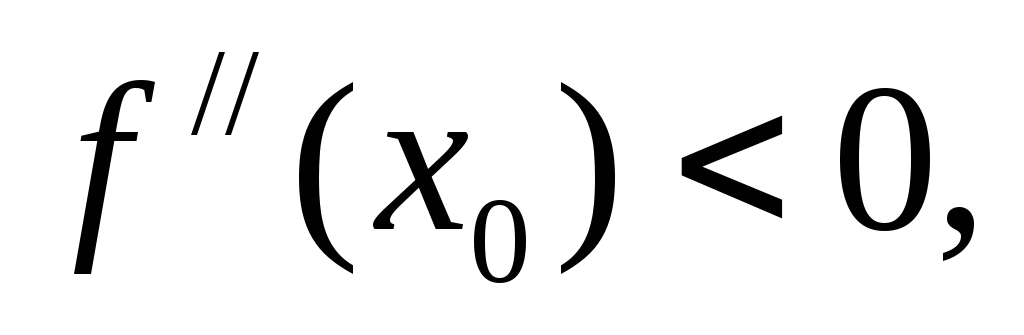 то
то
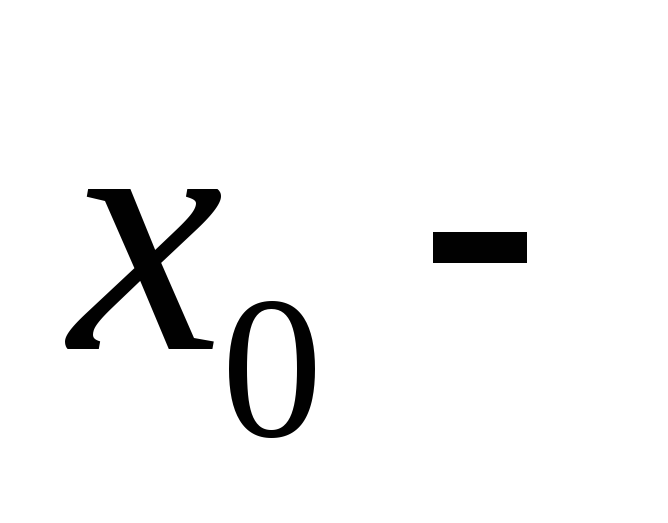 точка
максимума;
точка
максимума; -
если
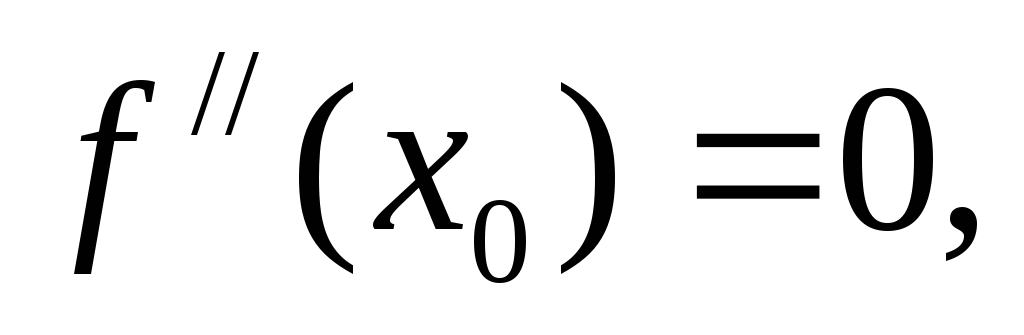 то требуется дополнительное исследование.
то требуется дополнительное исследование.
Доказательство:
Пусть
![]() - критическая точка функции
- критическая точка функции
![]() и существует
и существует
![]() .
Тогда существует производная
.
Тогда существует производная
![]() .
.
Пусть
![]() .
Тогда
.
Тогда
![]() возрастает в окрестности
возрастает в окрестности
![]() .
Следовательно,
.
Следовательно,
![]() меняет знак в окрестности
меняет знак в окрестности
![]() с “-” на “+”, т.е.
с “-” на “+”, т.е.
![]() - точка минимума функции
- точка минимума функции
![]() .
■
.
■
Пример.
Исследуем
функцию
![]() на экстремум. Найдем производную функции:
на экстремум. Найдем производную функции:
![]()
![]() .
Таким образом,
.
Таким образом,
![]() - критические точки данной функции. Так
как
- критические точки данной функции. Так
как
![]() ,
то
,
то
![]() ,
,
![]() .
По теореме точка
.
По теореме точка
![]() требует исследования знака первой
производной:
требует исследования знака первой
производной:
![]() при всех
при всех
![]() из некоторой окрестности этой точки,
поэтому точка
из некоторой окрестности этой точки,
поэтому точка
![]() не является точкой экстремума данной
функции. Так как
не является точкой экстремума данной
функции. Так как
![]() ,
то по теореме
,
то по теореме
![]() - точка минимума.
- точка минимума.
Понятие выпуклости и вогнутости функции
Определение
2. Функция
![]() называется выпуклой
на отрезке
называется выпуклой
на отрезке
![]() ,
если
,
если
![]() выполняется неравенство Йенсена
выполняется неравенство Йенсена
![]()
![]() .
.
Пример.
Покажем, что
функция
![]() является выпуклой на всей числовой оси.
Пусть
является выпуклой на всей числовой оси.
Пусть
![]() .
.
Рассмотрим
![]()
![]()
![]()
![]() .
.
Таким
образом,
![]() .
.
Определение
3. Функция
![]() называется выпуклой
на отрезке
называется выпуклой
на отрезке
![]() ,
если
,
если
![]() касательная, проведенная к графику
функции
касательная, проведенная к графику
функции
![]() в точке с абсциссой
в точке с абсциссой
![]() ,
проходит не выше хорды, стягивающей
точки с координатами
,
проходит не выше хорды, стягивающей
точки с координатами
![]() и
и
![]() .
(Рисунок)
.
(Рисунок)
Определение
4. Функция
![]() называется вогнутой
на отрезке
называется вогнутой
на отрезке
![]() ,
если
,
если
![]() выполняется неравенство
выполняется неравенство
![]() .
.
Замечание. Выпуклость функции называют выпуклостью вниз, а вогнутость – выпуклостью вверх.
Теорема 2. Критерий выпуклости
Для
того, чтобы функция
![]() ,
дифференцируемая на интервале
,
дифференцируемая на интервале
![]() была выпуклой на нем, необходимо и
достаточно, чтобы
была выпуклой на нем, необходимо и
достаточно, чтобы
![]() монотонно возрастала на этом интервале.
При этом строгому возрастанию
монотонно возрастала на этом интервале.
При этом строгому возрастанию
![]() соответствует строгая выпуклость
соответствует строгая выпуклость
![]() .
.
Доказательство:
Необходимость.
Пусть
![]() дифференцируема и выпукла на интервале
дифференцируема и выпукла на интервале
![]() .
Тогда из определения выпуклости имеем,
что
.
Тогда из определения выпуклости имеем,
что
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
Так как
.
Так как
![]() то
то
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
По теореме Лагранжа
.
По теореме Лагранжа
![]() ,
где
,
где
![]() .
.
Таким
образом,
![]() монотонно возрастает.
монотонно возрастает.
Достаточность.
Пусть
![]() монотонно возрастает на интервале
монотонно возрастает на интервале
![]() .
Тогда по теореме Лагранжа
.
Тогда по теореме Лагранжа
![]() ,
,
![]() ,
так как
,
так как
![]() ,
,
![]() ■
■
Теорема 3. Достаточное условие выпуклости
Функция
![]() выпукла на интервале
выпукла на интервале
![]() ,
если
,
если
![]() .
.
Доказательство:
Запишем
формулу Тейлора для функции
![]() :
:
![]() .
Так как
.
Так как
![]()
![]() ,
то
,
то
![]() .
■
.
■
Определение
5. Точку
![]() называют точкой
перегиба
функции
называют точкой
перегиба
функции
![]() ,
если
,
если
![]() функция выпукла (вогнута) и
функция выпукла (вогнута) и
![]() функция вогнута (выпукла).
функция вогнута (выпукла).
Теорема 4. Необходимое условие перегиба
Пусть
функция
![]() имеет вторую производную в точке
имеет вторую производную в точке
![]() .
Тогда, если
.
Тогда, если
![]() является точкой перегиба, то
является точкой перегиба, то
![]() .
.
Теорема 5. Достаточное условие перегиба
Пусть
![]() и
и
![]() .
Тогда, если вторая производная меняет
свой знак при прохождении через точку
.
Тогда, если вторая производная меняет
свой знак при прохождении через точку
![]() ,
то
,
то
![]() является точкой перегиба.
является точкой перегиба.
