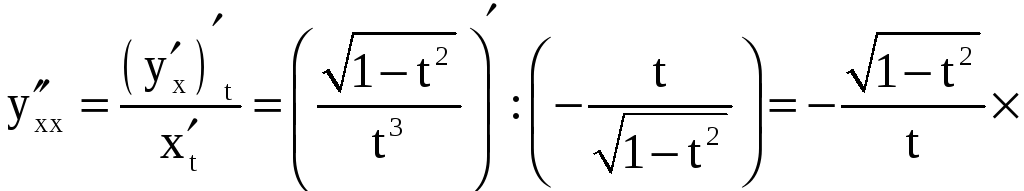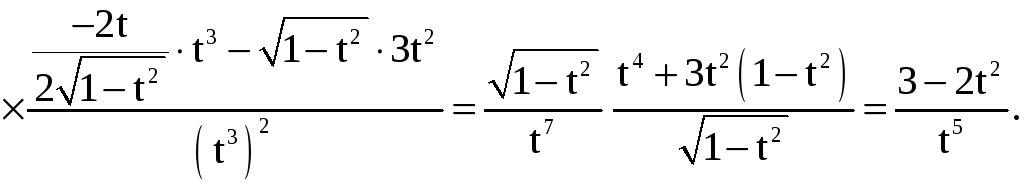- •V. Дифференциальное исчисление функции одного переменного
- •1. Производная. Правила дифференцирования
- •2. Таблица производных
- •3. Правила дифференцирования
- •4. Производные высших порядков
- •5. Дифференцирование функций, заданных неявно или параметрически Говорят, что уравнение
- •6. Уравнения касательной и нормали
- •7. Дифференциал первого порядка
- •8. Дифференциалы высших порядков. Формула Тейлора
- •9. Раскрытие неопределённостей по правилу Лопиталя
- •Задание 5.2
- •Задание 5.3
- •Задание 5.4
- •Задание 5.5
- •Задание 5.6
- •Задание 5.7
- •Задание 5.8
- •Задание 5.14
- •Задание 5.15
- •Задание 5.16
V. Дифференциальное исчисление функции одного переменного
1. Производная. Правила дифференцирования
Пусть функция
![]() определена в некоторой окрестности
точки
определена в некоторой окрестности
точки
![]() .
Придадим значению переменной
.
Придадим значению переменной
![]() в точке
в точке
![]() приращение
приращение
![]() ,
при этом
,
при этом
![]() получит приращение
получит приращение
![]() .
Если существует конечный предел
.
Если существует конечный предел
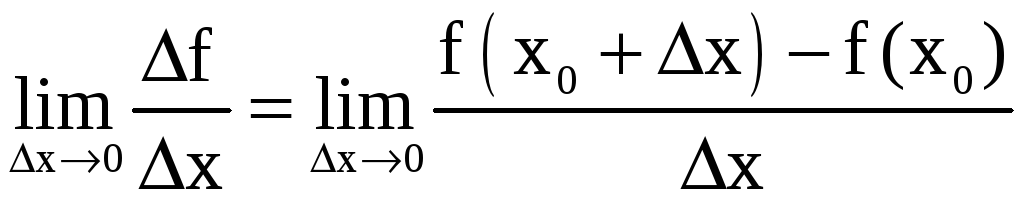 ,
,
то
он называется производной функции f(x)
в точке x0
и обозначается
![]() .
Общеприняты и другие обозначения
производной функции
.
Общеприняты и другие обозначения
производной функции
![]() :
:
![]() ,
,
![]() ;
если же
;
если же
![]() зависит от значения переменной
зависит от значения переменной
![]() (времени), то часто вместо
(времени), то часто вместо
![]() пишут
пишут
![]() .
Если вышеуказанный предел существует
в каждой точке интервала
.
Если вышеуказанный предел существует
в каждой точке интервала
![]() ,
то
,
то
![]() становится функцией, определённой на
(a,
b).
становится функцией, определённой на
(a,
b).
Пример 1.
Используя определение производной,
найти производную функции
![]() .
.
Решение.
Придадим значению переменной x приращение
x,
тогда функция
![]() получит приращение
получит приращение
y = f(x + x) – f(x) = sin (2(x + x) + 1) – sin (2x + 1) =
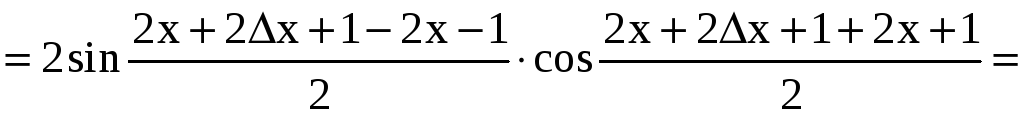
= 2 sin x cos (2x + x + 1).
Отсюда находим
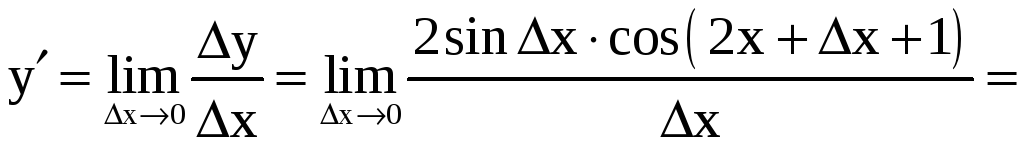
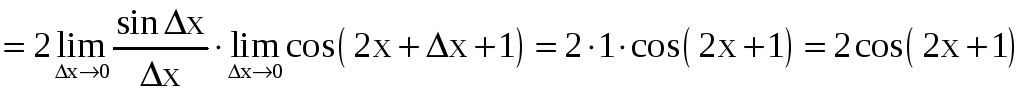 .
.
Таким образом,
![]() .
.
Процесс нахождения производной часто называют дифференцированием.
2. Таблица производных
(Здесь и ниже C – постоянная величина.)
![]() ;
; ![]() ;
; ![]() ;
;
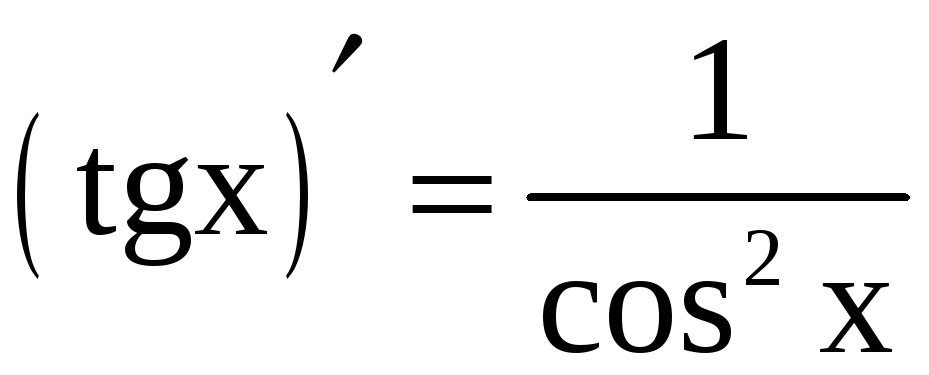 ;
;
![]() ;
; 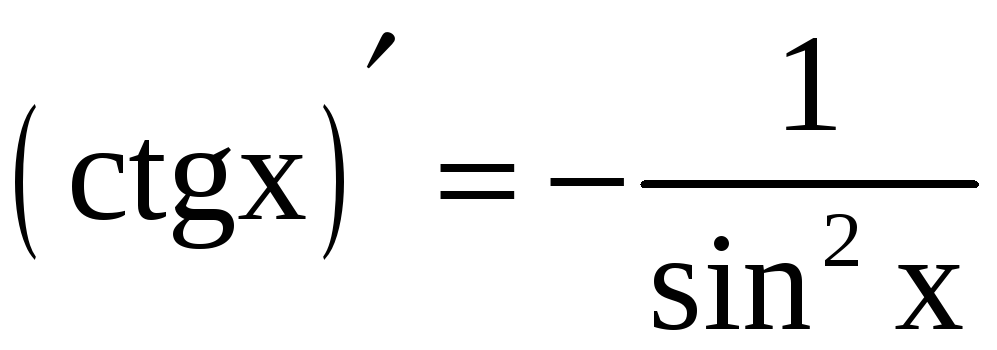 ;
;
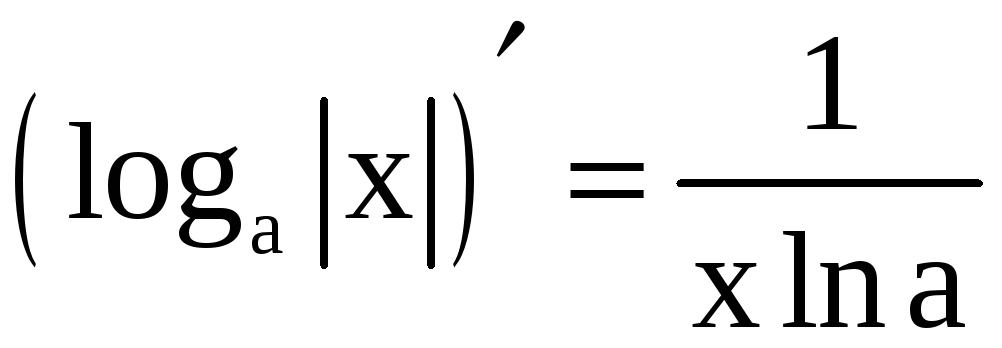 ;
; 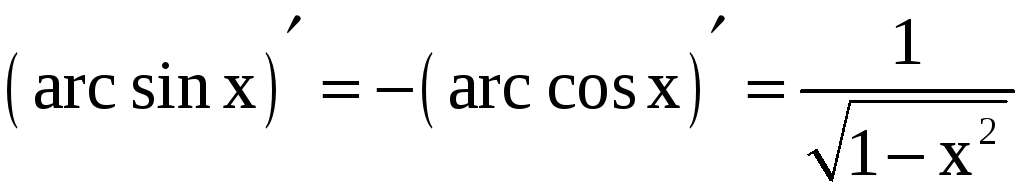 ;
;
![]() ;
; 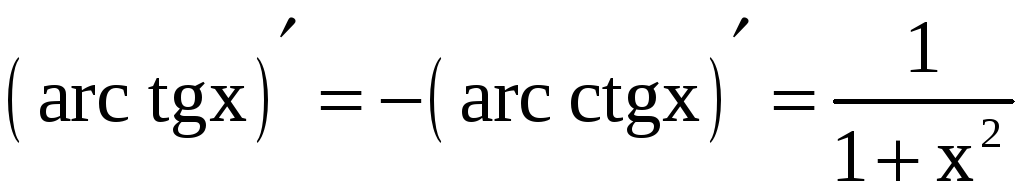 .
.
3. Правила дифференцирования
Если
функции f(x)
и g(x)
имеют производные
![]() и
и
![]() ,
то функции
,
то функции
![]() ,
,
![]() ,
,
![]() ,
,
![]() также имеют производные (последняя –
при условии
также имеют производные (последняя –
при условии
![]() ),
и при этом
),
и при этом
![]() ;
; ![]() ;
;
![]() ;
; 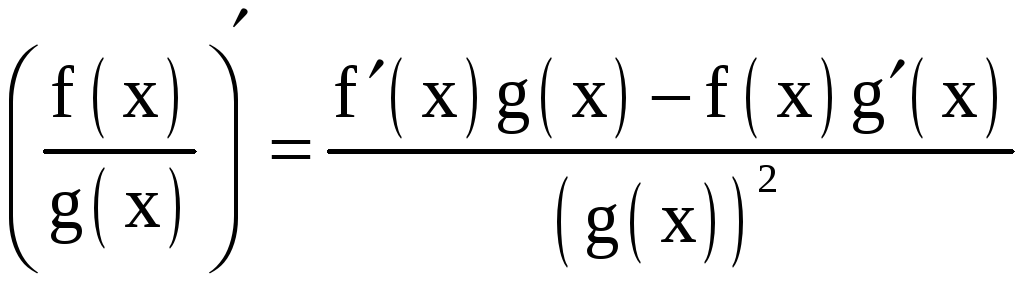 .
.
Теорема 1
(о производной
сложной функции).
Пусть функции
![]() ,
определённая в окрестности точки x0,
и z = g (y), определённая в окрестности
точки
,
определённая в окрестности точки x0,
и z = g (y), определённая в окрестности
точки
![]() ,
обладают тем свойством, что существуют
производные
,
обладают тем свойством, что существуют
производные
![]() и
и
![]() .
Тогда функция
.
Тогда функция
![]() имеет производную в точке x0
и при этом
имеет производную в точке x0
и при этом
![]() .
.
Пример 2. Найти производные функций:
а)
![]() ; б)
; б)
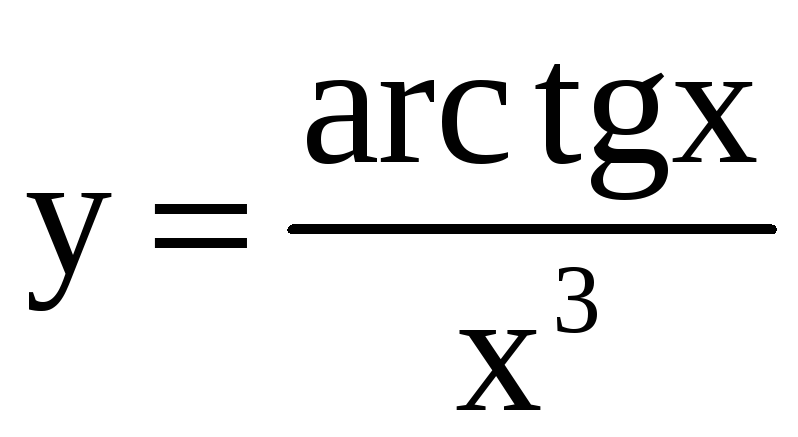 ;
;
в)
![]() ; г)
; г)
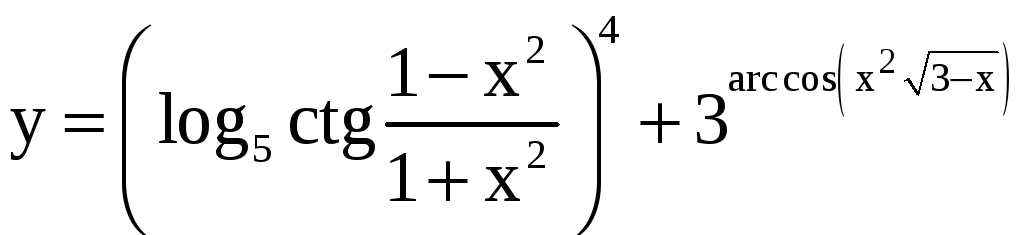 .
.
Решение. а), б) Применяя правила дифференцирования, находим
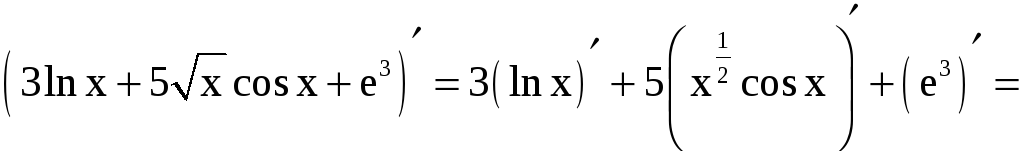
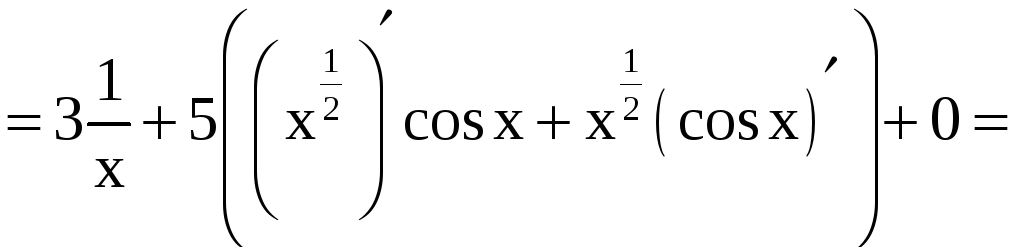
=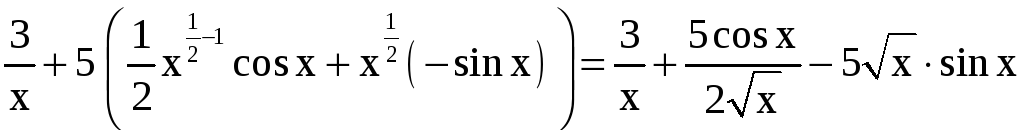 ;
;
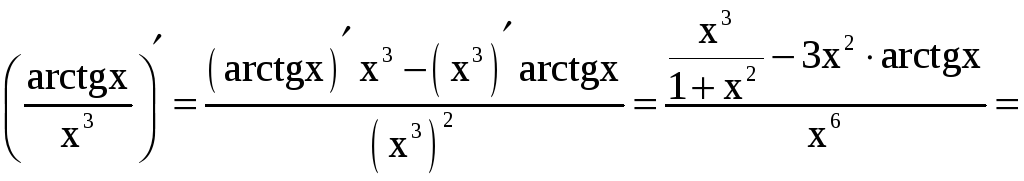

в), г) Применяя теорему о дифференцировании сложной функции, находим

=![]() ;
;
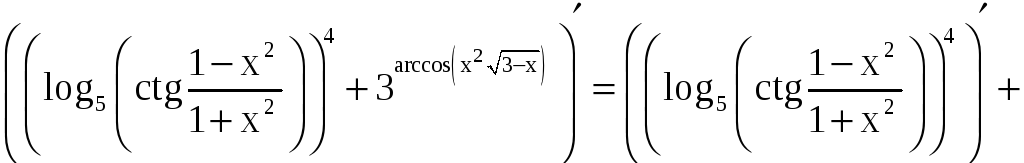
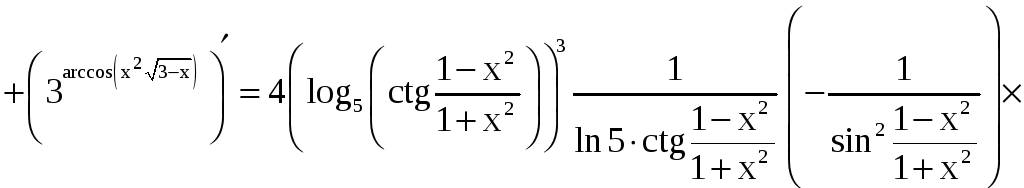
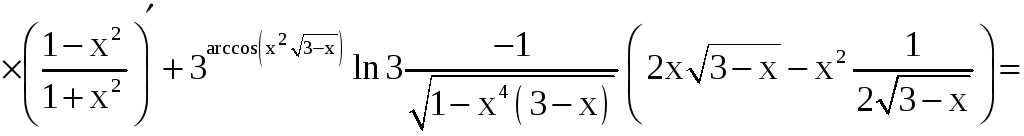
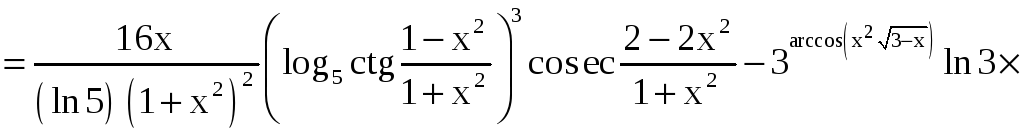
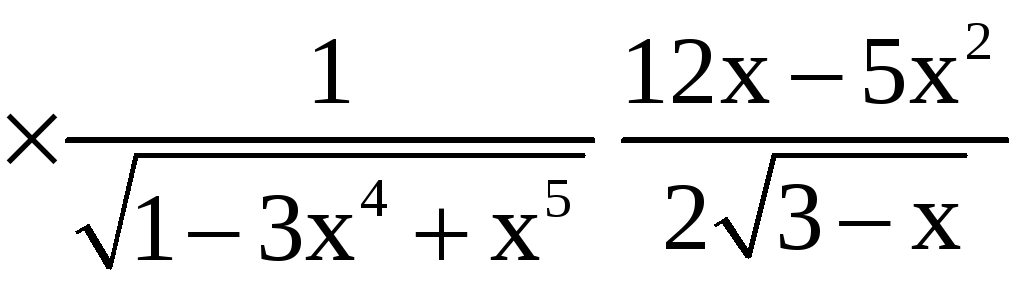 .
.
Пример 3.
Показать,
что функция
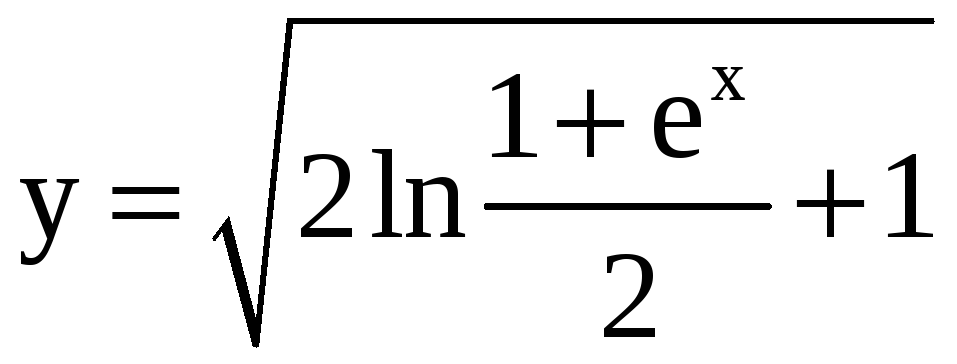 удовлетворяет уравнению
удовлетворяет уравнению
![]() . (1)
. (1)
Решение. Найдём производную функции
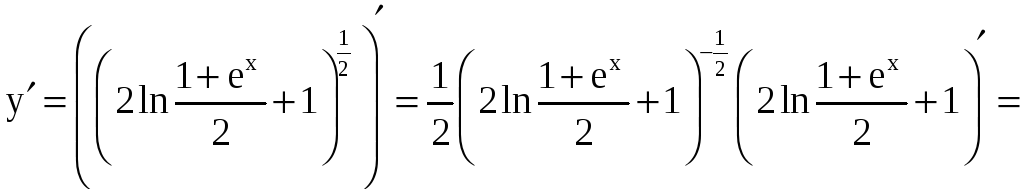
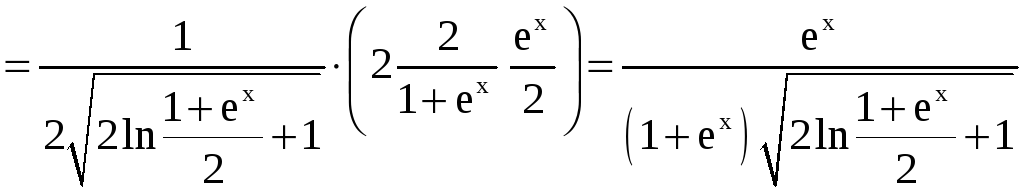 .
.
Подставив это выражение в (1), получим
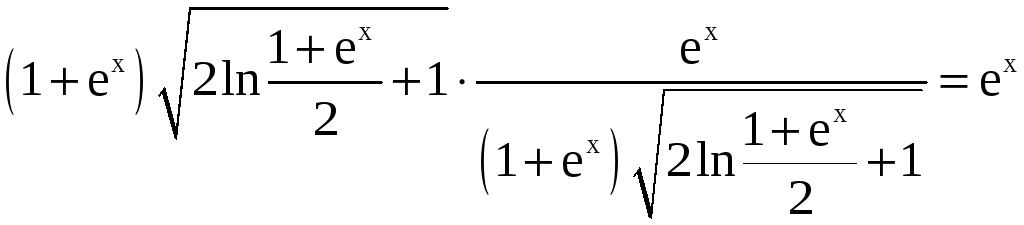 ,
,
или
![]() .
.
Это и доказывает, что наша функция удовлетворяет уравнению (1).
Для дифференцирования
степенно-показательной (вида
![]() )
и некоторых других функций удобно
пользоваться так называемым логарифмическим
дифференцированием.
)
и некоторых других функций удобно
пользоваться так называемым логарифмическим
дифференцированием.
Пример 4. Найти производные функций:
а)
![]() ; б)
; б)
 .
.
Решение. а) Предварительно
прологарифмируем обе части равенства
![]() ,
имеем
,
имеем
![]() .
.
Продифференцируем
обе части последнего равенства, считая
![]() сложной функцией от
сложной функцией от
![]() :
:
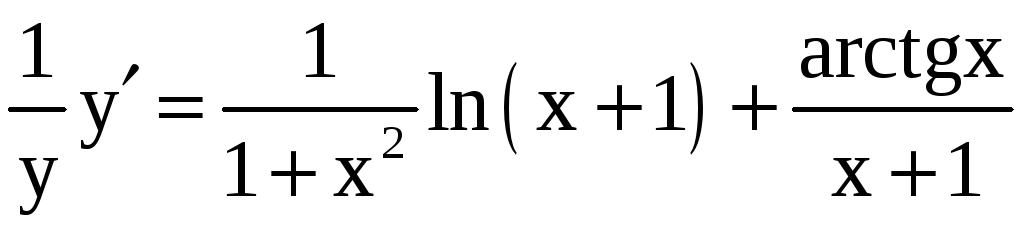 ;
;
отсюда находим
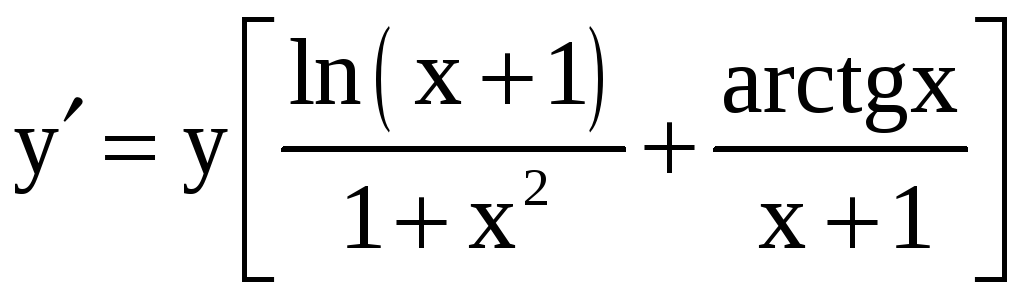 .
.
Подставив
![]() ,
получим
,
получим
 .
.
б) действуя так же, находим
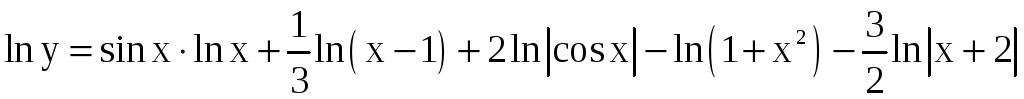 ;
;
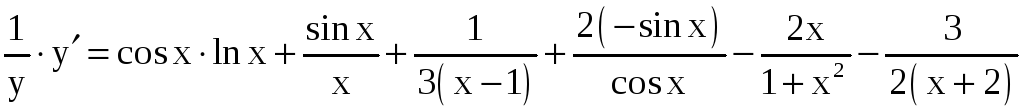 ;
;
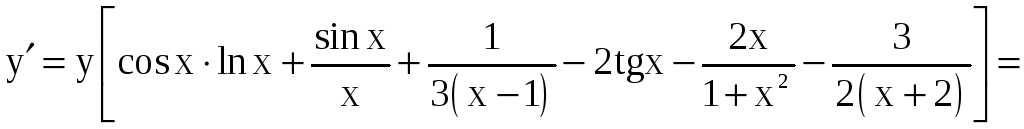
4. Производные высших порядков
Производную
от производной
![]() называют второй производной от функции
f(x)
и обозначают
называют второй производной от функции
f(x)
и обозначают
![]()
![]() .
Производную от
.
Производную от
![]() называют третьей производной функции
f(x)
и обозначают
называют третьей производной функции
f(x)
и обозначают
![]() .
Таким образом,
.
Таким образом,
![]() ,
,
![]() ,
. . . ,
,
. . . ,
![]() ,
. . .
,
. . .
Общепринятыми
являются и другие обозначения производной
n-го порядка функции y = f(x):
![]() или
или
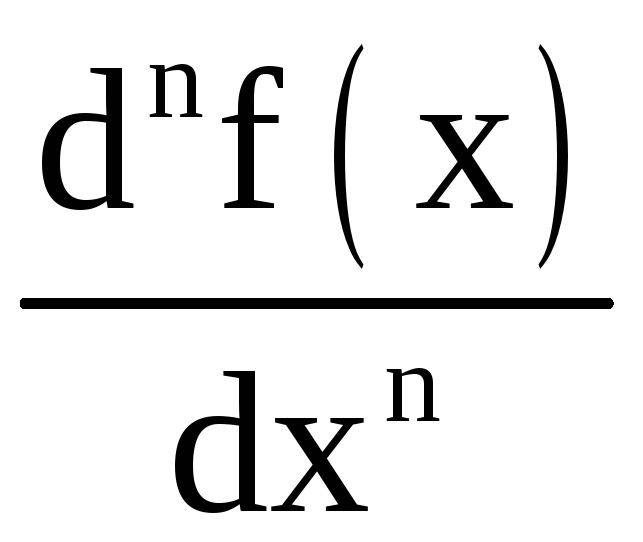 .
.
Пример 5.
Найти
![]() ,
если y = ln(sinx) .
,
если y = ln(sinx) .
Решение.
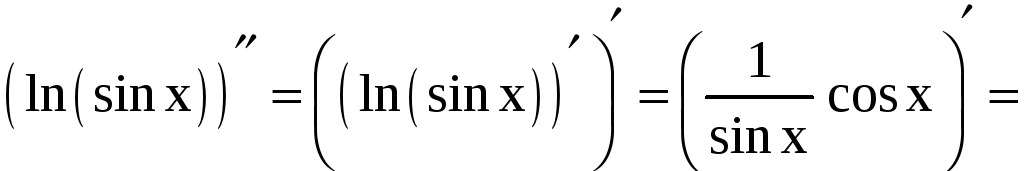
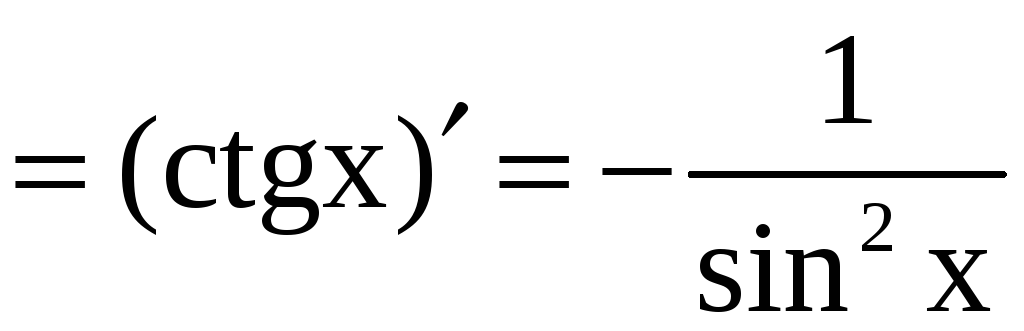 ;
;
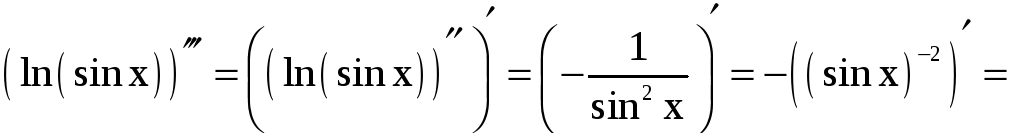
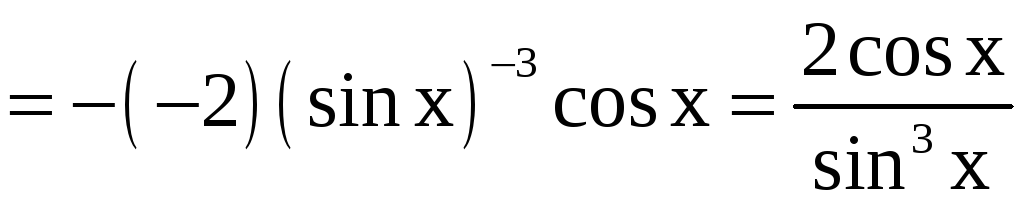 .
.
5. Дифференцирование функций, заданных неявно или параметрически Говорят, что уравнение
F(x, y) = 0 (2)
неявно задаёт
функцию y = f(x) в интервале (a, b), если для
любого
![]() уравнение F(x0;
y)=0 имеет единственное решение y0
= f(x0).
уравнение F(x0;
y)=0 имеет единственное решение y0
= f(x0).
Для нахождения
производной функции
![]() ,
заданной неявно уравнением (2), следует
продифференцировать обе части равенства
(2), считая
,
заданной неявно уравнением (2), следует
продифференцировать обе части равенства
(2), считая
![]() функцией от
функцией от
![]() ;
затем полученное уравнение, в которое
будут входить x, y и
;
затем полученное уравнение, в которое
будут входить x, y и
![]() ,
следует разрешить относительно
,
следует разрешить относительно
![]() .
.
Для нахождения
![]() равенство (2) дифференцируется дважды,
в результате чего получается уравнение,
содержащее x, y,
равенство (2) дифференцируется дважды,
в результате чего получается уравнение,
содержащее x, y,
![]() ,
,
![]() ,
которое следует разрешить относительно
,
которое следует разрешить относительно
![]() ,
затем вместо
,
затем вместо
![]() подставить функцию от x и y, найденную
указанным выше способом.
подставить функцию от x и y, найденную
указанным выше способом.
Пример 6. Найти
значения
![]() ,
,
![]() ,
если функция y задана неявно уравнением
,
если функция y задана неявно уравнением
![]() . (3)
. (3)
Решение.
Считая y функцией от x, продифференцируем
обе части равенства (3):
![]() ;
;
![]() ;
; ![]() . (4)
. (4)
Отсюда находим
 ; (5)
; (5)
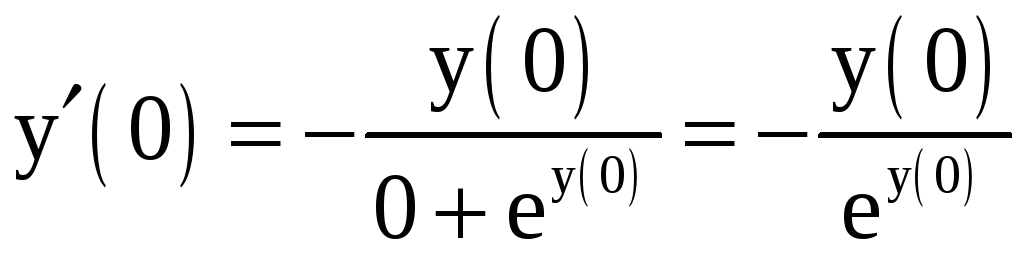 .
.
Для нахождения y(0) в равенстве (3) положим x = 0:
![]() ;
; ![]() ; y(0)
= 1.
; y(0)
= 1.
Таким образом,
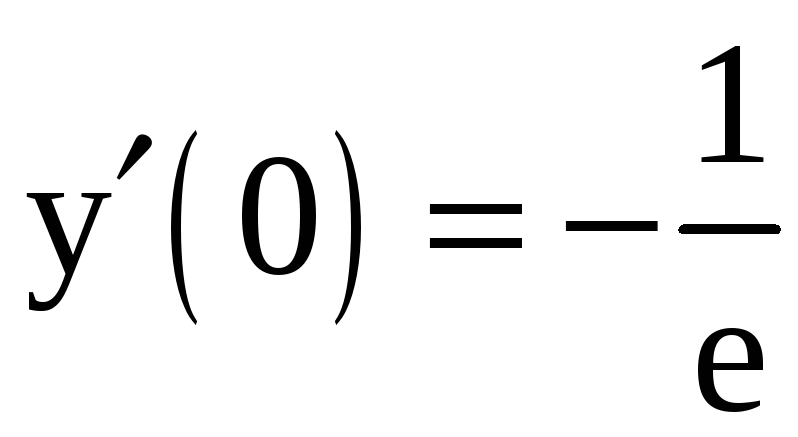 .
.
Найдём
![]() ,
для чего продифференцируем равенство
(4):
,
для чего продифференцируем равенство
(4):
![]() ;
;
![]() ;
;
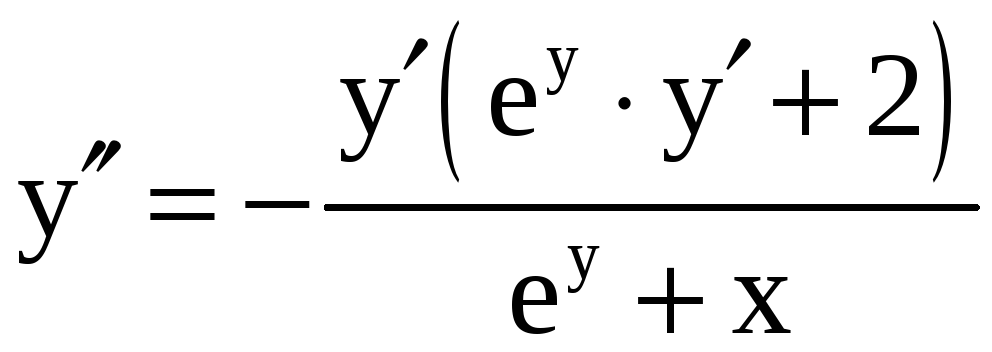 .
.
Подставив в
последнем равенстве вместо
![]() выражение (5), получим
выражение (5), получим
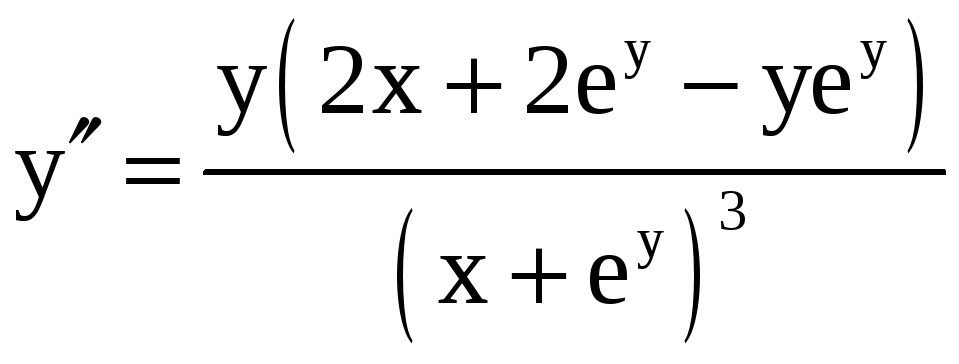 ,
,
откуда находим
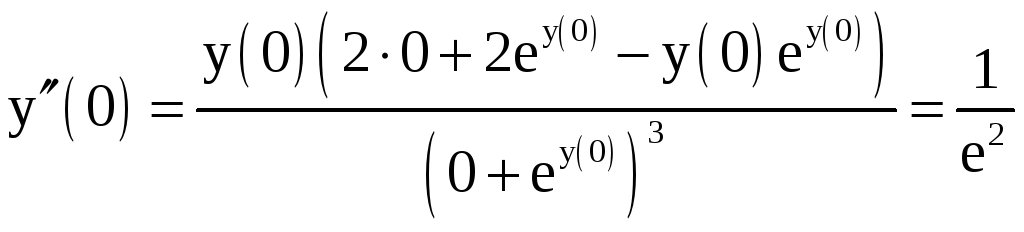 .
.
Если функция y = y(x) задана параметрическими уравнениями

то при условии
существования производных
![]() ,
,
![]() и
и
![]() существует производная
существует производная
![]() и при этом
и при этом
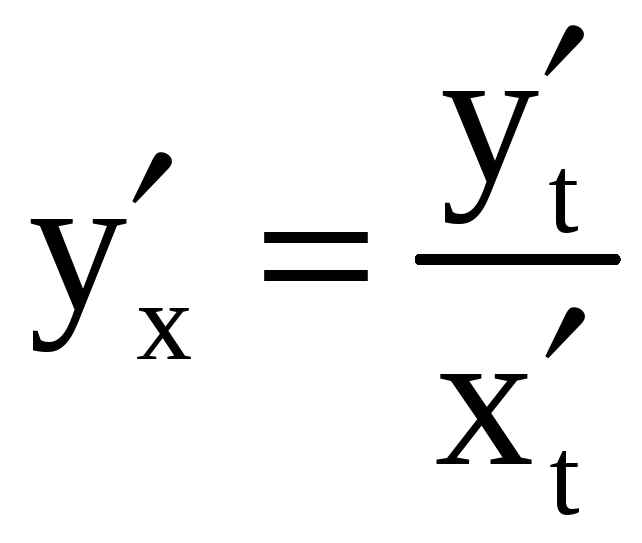 .
.
Вторая производная
![]() находится по формуле
находится по формуле
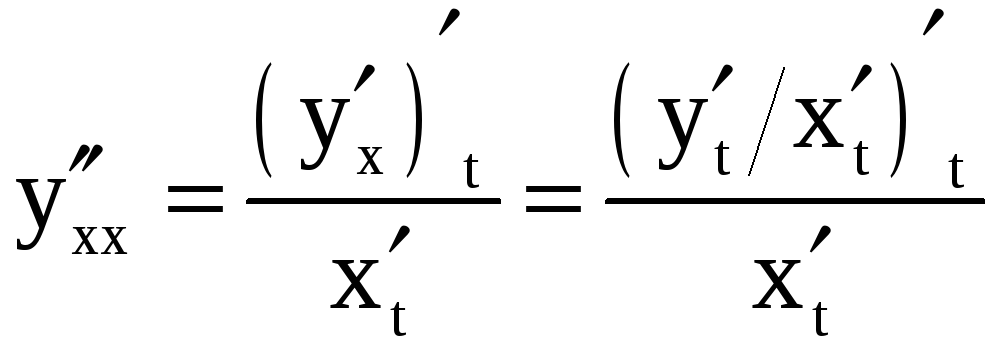 ,
,
или (что то же самое)
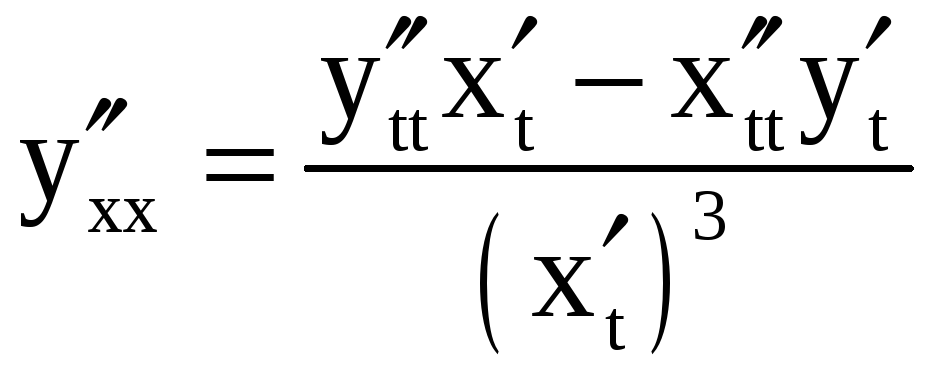 .
.
Пример 7.
Найти
![]() ,
,
![]() ,
если
,
если

Решение. Имеем:
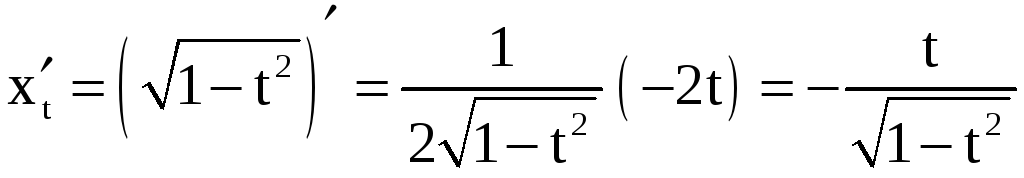 ;
;
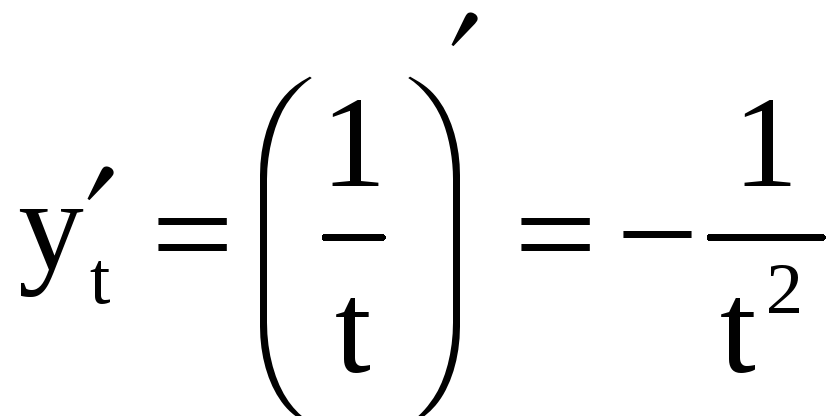 ;
;
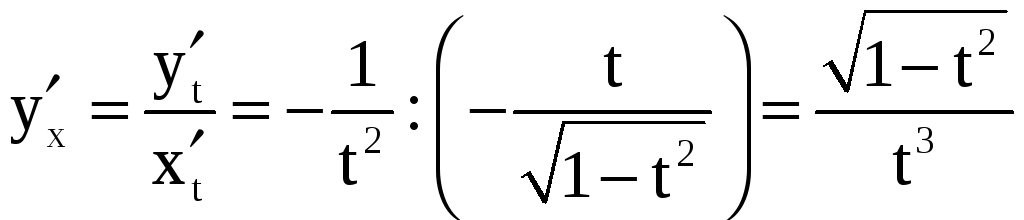 ;
;