
- •I. Комплексные числа. Многочлены
- •1. Комплексные числa
- •Решение. А) Перепишем первое уравнение в виде . Из геометрического смысла модуля разности двух комплексных чисел следует, что множество решений
- •2. Многочлены
- •Задание 1.1
- •Задание 1.2
- •Задание 1.3
- •Задание 1.4
- •Задание 1.5
- •Задание 1.6
- •Задание 1.7
I. Комплексные числа. Многочлены
1. Комплексные числa
Комплексными
числами называются упорядоченные пары
![]() действительных чисел
действительных чисел
![]() и
и
![]() ,
для которых введены понятия равенства
и операции сложения и умножения:
,
для которых введены понятия равенства
и операции сложения и умножения:
![]() если
если
![]() , (1)
, (1)
![]() (2)
(2)
![]() . (3)
. (3)
Из формул (2) и (3) вытекают, в частности, соотношения
![]()
![]() ,
,
которые
показывают, что операции над комплексными
числами вида
![]() совпадают с операциями над действительными
числами
совпадают с операциями над действительными
числами
![]() .
Поэтому
комплексные
числа
вида
.
Поэтому
комплексные
числа
вида
![]() отождествляются
с действительными
числами
отождествляются
с действительными
числами
![]() .
Особую роль играет число
.
Особую роль играет число
![]() ,
которое называется мнимой единицей.
,
которое называется мнимой единицей.
Из формул (2), (3) вытекают также равенства:
![]() ,
,
![]() ,
,
![]() .
.
Итак,
каждое комплексное число
![]() можно представить в виде
можно представить в виде
![]() .
Такая запись комплексного числа
называется алгебраической формой
комплексного числа. Число
.
Такая запись комплексного числа
называется алгебраической формой
комплексного числа. Число
![]() называется действительной частью, а
называется действительной частью, а
![]() – мнимой частью комплексного числа
– мнимой частью комплексного числа
![]() .
Для них приняты следующие обозначения:
.
Для них приняты следующие обозначения:
![]() .
.
Комплексное
число
![]() называется сопряженным с комплексным
числом
называется сопряженным с комплексным
числом
![]() .
.
Число
![]() называется модулем комплексного числа
называется модулем комплексного числа
![]() .
Очевидно,
.
Очевидно,
![]() ,
причем,
,
причем,
![]() ,
тогда и только тогда, когда
,
тогда и только тогда, когда
![]() .
Модуль действительного числа совпадает
с абсолютной величиной этого числа.
.
Модуль действительного числа совпадает
с абсолютной величиной этого числа.
Отметим
две формулы:
![]() ,
,
![]() ,
которые вытекают из определений
,
которые вытекают из определений
![]() и равенства
и равенства
![]() .
.
Вычитание и деление комплексных чисел являются действиями, обратными соответственно сложению и умножению.
Если ![]() ,
,
![]() ,
,
то ![]()
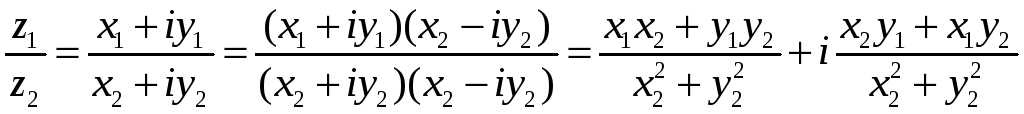 .
.
Комплексное
число как упорядоченная пара вещественных
чисел определяет точку
![]() на плоскости или вектор
на плоскости или вектор
![]() (рис. 1).
(рис. 1).
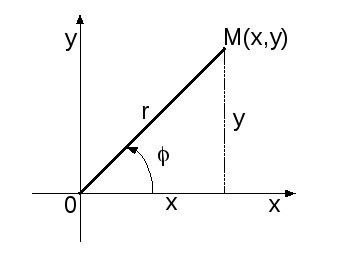
Рис. 1
Плоскость,
на которой изображаются комплексные
числа, называется комплексной плоскостью.
Положение точки
![]() на комплексной плоскости однозначно
определяется не только декартовыми
координатами
на комплексной плоскости однозначно
определяется не только декартовыми
координатами
![]() ,
но и полярными координатами
,
но и полярными координатами
![]() ,
где
,
где
![]() – длина вектора
– длина вектора
![]() ,
а
,
а
![]() – угол между действительной осью и
вектором
– угол между действительной осью и
вектором
![]() ,
отсчитываемый от положительного
направления действительной оси. При
этом, если отсчет ведется против часовой
стрелки, то величина угла считается
положительной, а если по часовой стрелке
– отрицательной. Этот угол называется
аргументом комплексного числа
,
отсчитываемый от положительного
направления действительной оси. При
этом, если отсчет ведется против часовой
стрелки, то величина угла считается
положительной, а если по часовой стрелке
– отрицательной. Этот угол называется
аргументом комплексного числа
![]() и обозначается так:
и обозначается так:
![]() .
Для числа
.
Для числа
![]() аргумент не определяется, поэтому во
всех дальнейших рассуждениях, связанных
с понятием аргумента, предполагается,
что
аргумент не определяется, поэтому во
всех дальнейших рассуждениях, связанных
с понятием аргумента, предполагается,
что
![]() .
.
Угол
![]() определяется с точностью до
определяется с точностью до
![]() ,
где
,
где
![]() – целое число. Значение аргумента,
заключенное между
– целое число. Значение аргумента,
заключенное между
![]() и
и
![]() ,
называется его главным значением и
обозначается
,
называется его главным значением и
обозначается
![]() .
Таким образом,
.
Таким образом,
![]() .
.
При этом
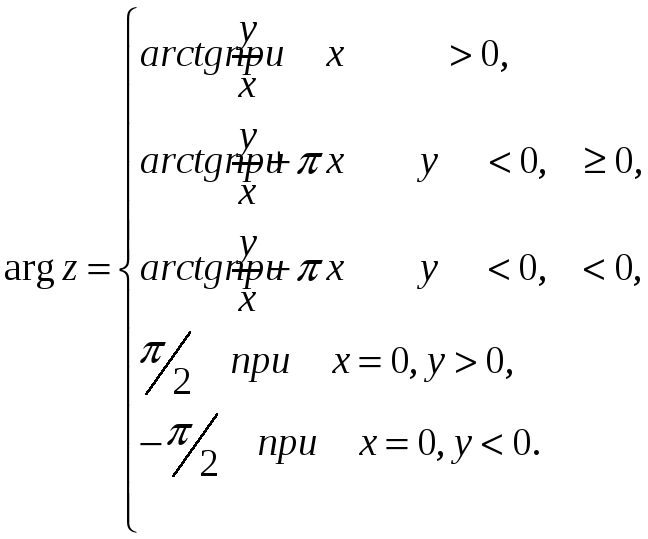
Из рис.1 видно, что
![]()
![]()
Следовательно,
любое комплексное число
![]() можно представить в виде
можно представить в виде
![]() (4)
(4)
Запись комплексного числа в виде (4) называется тригонометрической формой комплексного числа.
Если
![]() ,
то по формуле (4) имеем
,
то по формуле (4) имеем
![]() .
.
Комплексное
число
![]() обозначается символом
обозначается символом
![]() ,
то есть функция
,
то есть функция
![]() для любого вещественного числа
для любого вещественного числа
![]() определяется формулой Эйлера:
определяется формулой Эйлера:
![]() . (5)
. (5)
Подставляя (5) в (4), получаем показательную форму комплексного числа:
![]() .
.
Заменим
![]() на
на
![]() в равенстве (5):
в равенстве (5):
![]() . (6)
. (6)
Складывая и вычитая равенства (5) и (6), получаем формулы Эйлера:
![]()
![]()
Функция
![]() обладает обычными свойствами показательной
функции, как если бы число
обладает обычными свойствами показательной
функции, как если бы число
![]() было действительным.
было действительным.
Отметим основные из них:
![]() (7)
(7)
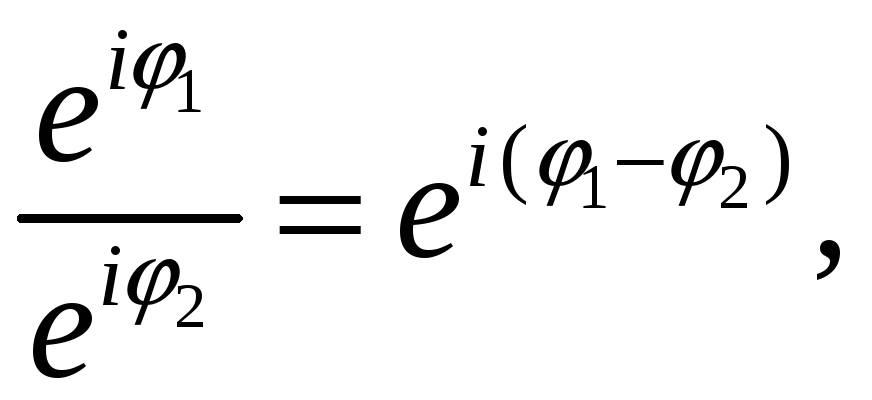 (8)
(8)
![]()
![]() . (9)
. (9)
Из (9) и (5) вытекает формула Муавра:
![]()
![]() .
.
С помощью (7), (8) легко получаются формулы умножения и деления комплексных чисел, записанных в показательной форме:
![]() ,
,
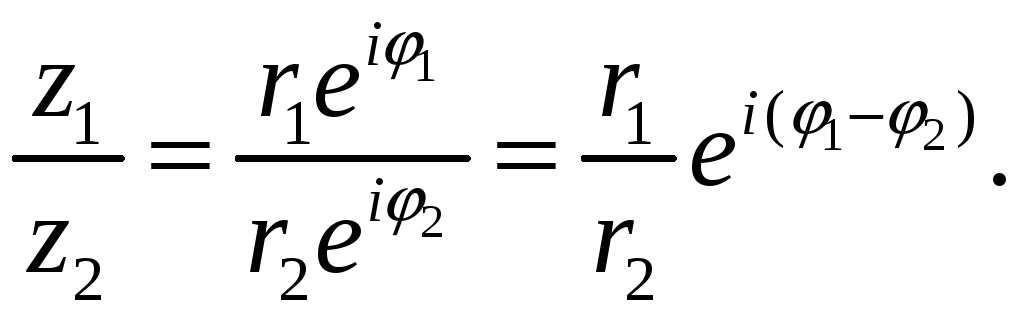
Корень
из комплексного числа
![]() имеет
имеет
![]() различных значений и находится по
формуле
различных значений и находится по
формуле
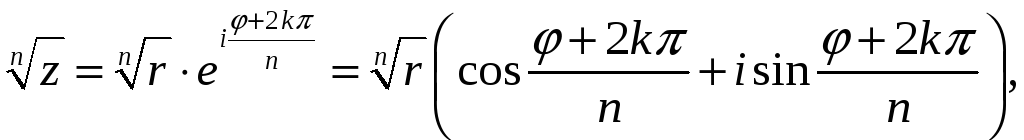
где
![]()
Модуль
разности
![]() чисел равен расстоянию между точками
z1
и z2
комплексной плоскости.
чисел равен расстоянию между точками
z1
и z2
комплексной плоскости.
Пример 1. Найти сумму, произведение и частное чисел
z1 = –1+2i и z2 = 2 – 3i .
Решение.
![]() ;
;
![]()
![]() ;
;
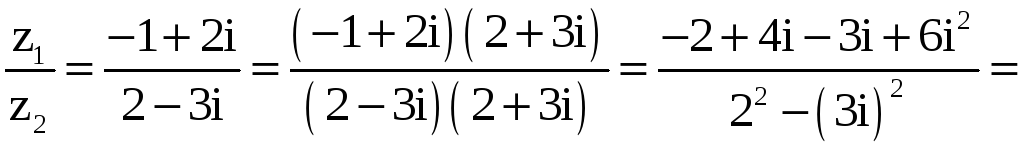
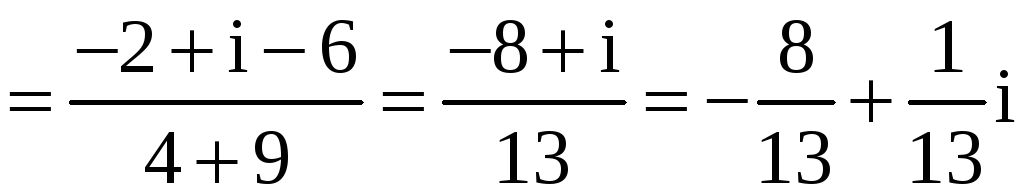 .
.
Пример 2.
Решить уравнение
![]() .
.
Решение. Воспользуемся формулой корней квадратного уравнения
 .
.
Таким образом,
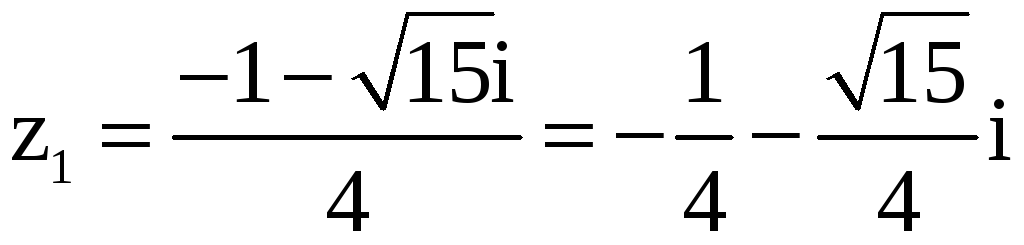 ,
, 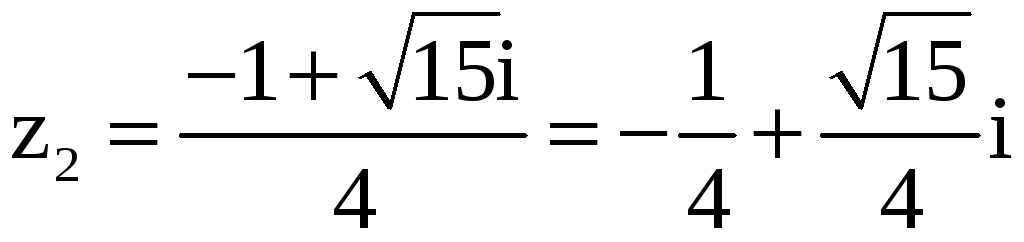 .
.
Пример 3. Выполнить
действия. Ответ записать в алгебраической
форме
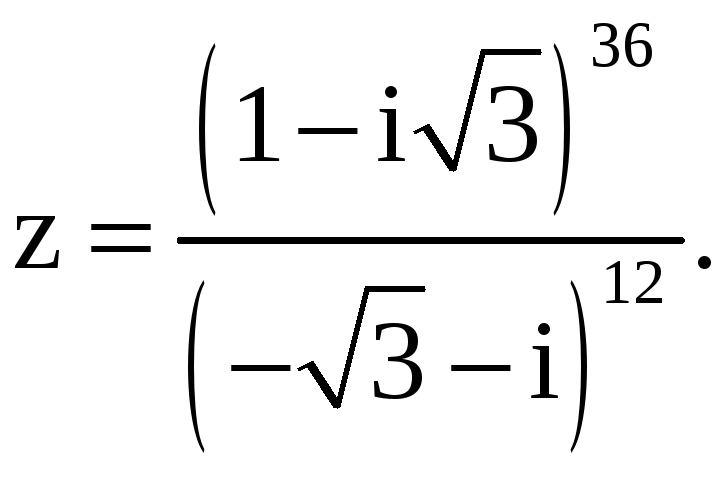
Решение.
 ,
,
где
![]() модуль
комплексного числа
модуль
комплексного числа
![]() ;
;
![]() главное
значение аргумента комплексного числа.
главное
значение аргумента комплексного числа.
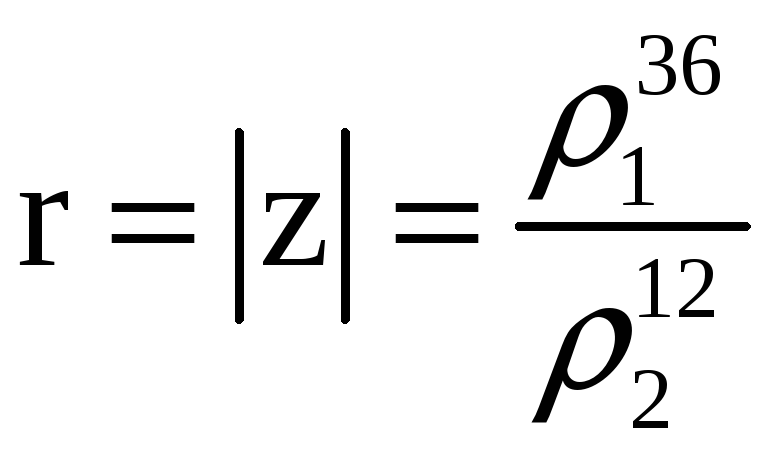 ;
; ![]() ;
; ![]() ;
;
![]() .
.
Найдем модули и главные значения аргументов комплексного числа.
Считаем, что
![]() .
.
![]() .
.
![]()
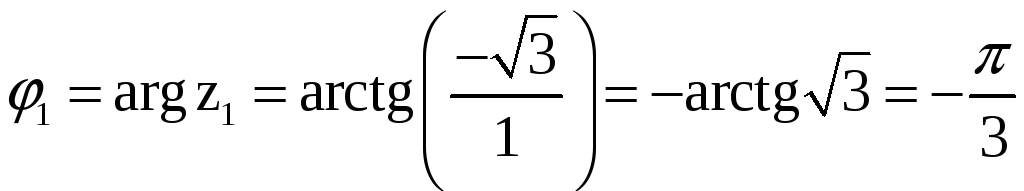 .
.
![]()
 .
.
![]()
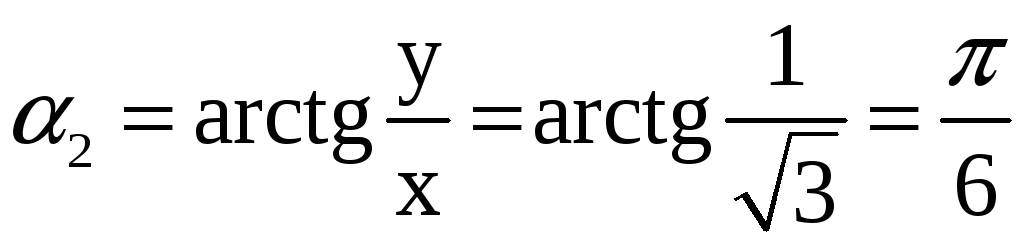
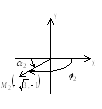 ,
,
 .
.
Тогда
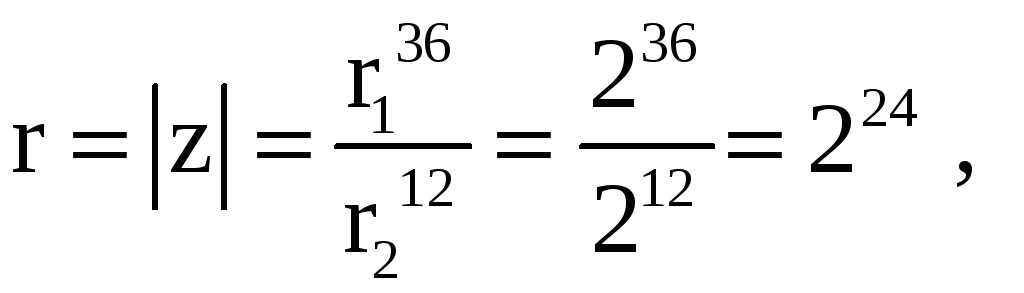
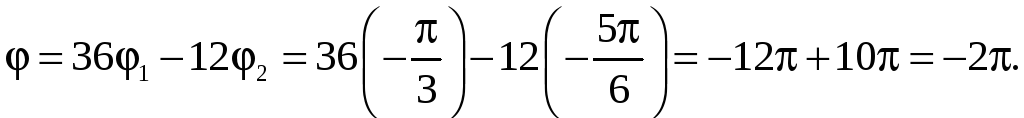
![]() .
.
Пример 4. Решить уравнение
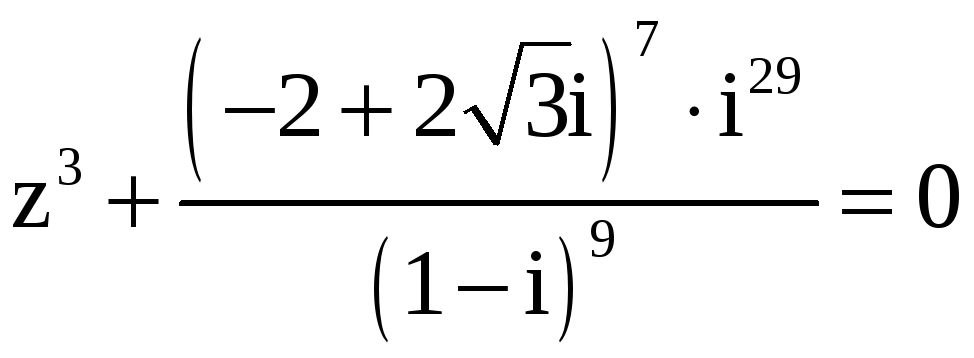 .
.
Решение.
Обозначим
![]() ,
,
![]() ,
,
![]() .
Найдём
.
Найдём
![]() ,
,
![]() ,
,
![]() .
Для этого представим каждое из чисел
z1,
z2,
z3
в показательной форме:
.
Для этого представим каждое из чисел
z1,
z2,
z3
в показательной форме:
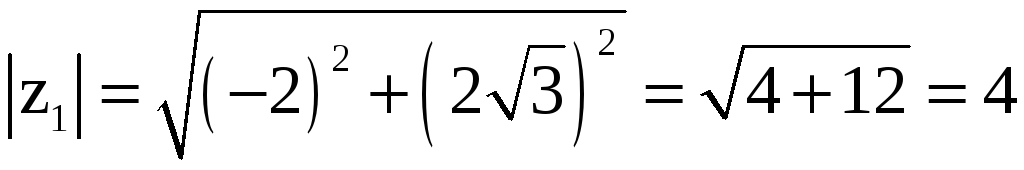 ,
,

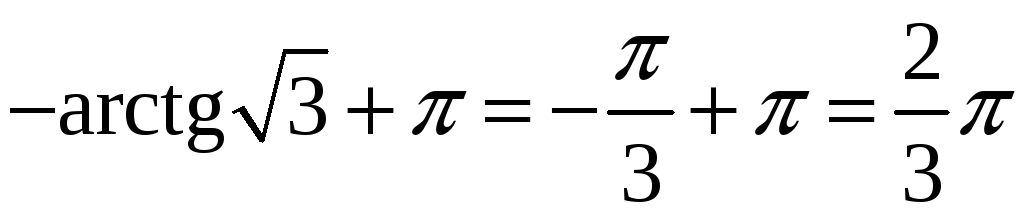 ,
, ![]() ;
;
![]() ,
, ![]() ,
,
![]() ;
;
![]() ,
, 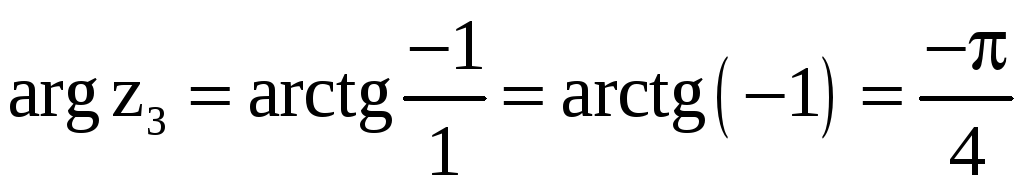 ,
,
![]() .
.
Имеем
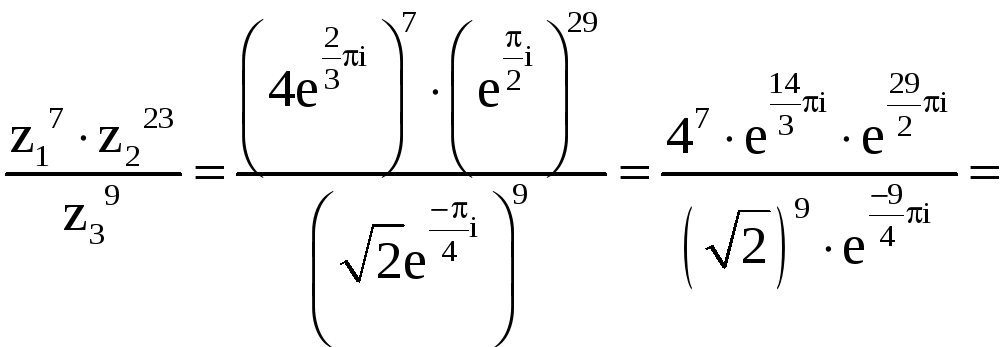
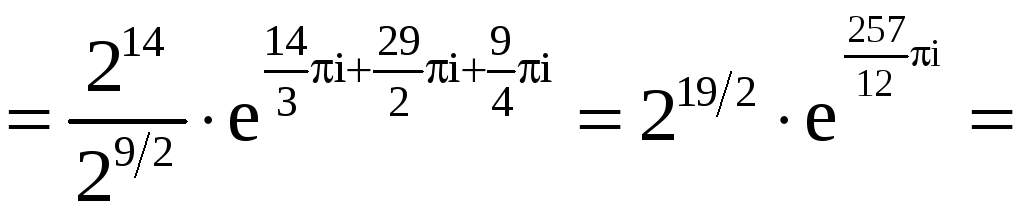
![]() .
.
Наше уравнение
принимает вид
![]() или
или
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Таким образом,
корни исходного уравнения являются
корнями третьей степени числа
![]() .
Имеем
.
Имеем
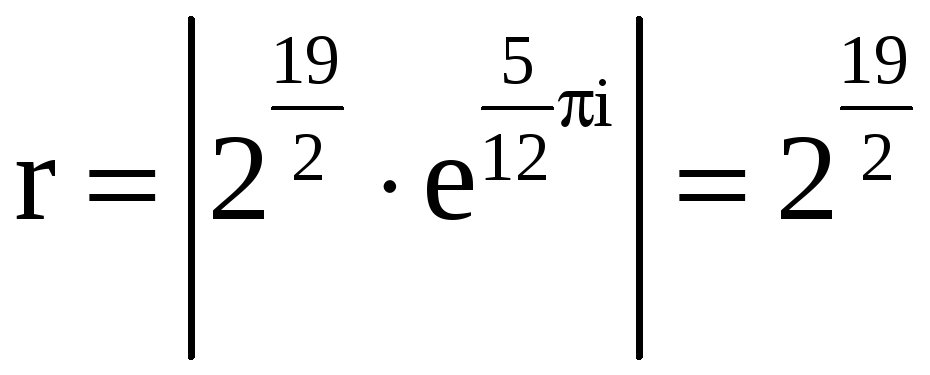 ,
,
 .
Найдём наши корни по формуле
.
Найдём наши корни по формуле
 ,
k = 0, 1, 2.
,
k = 0, 1, 2.
Отсюда получаем
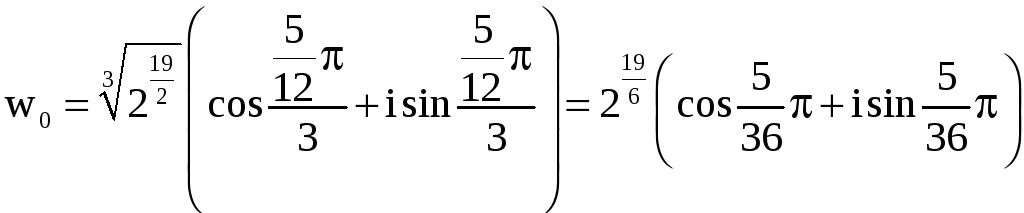 ,
,
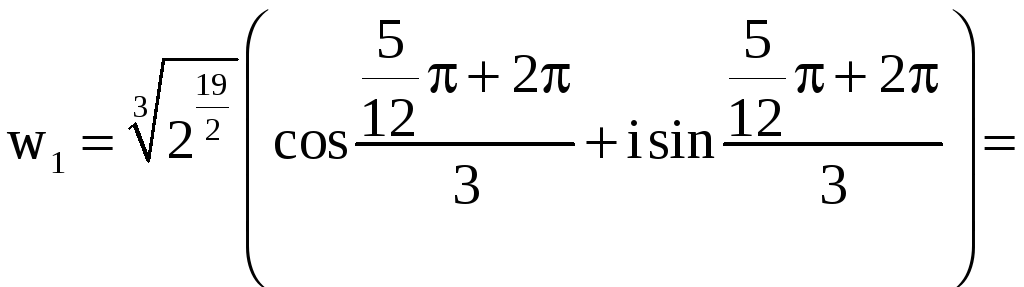
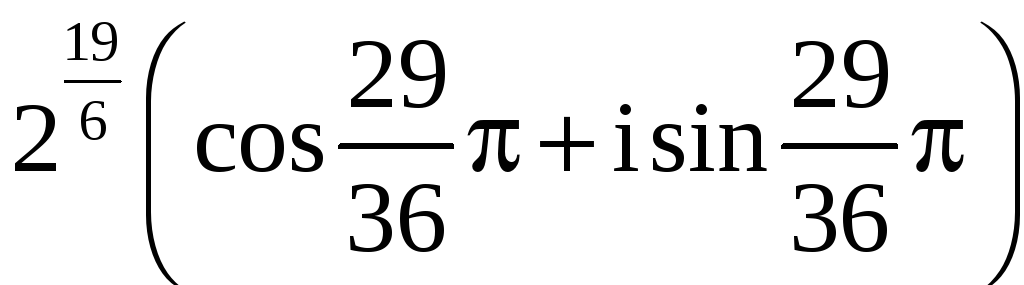 ,
,
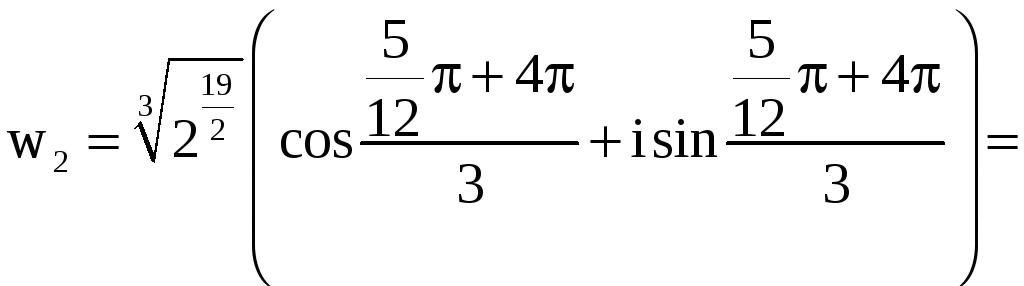
 .
.
Числа w0 , w1 , w2 (записанные в тригонометрической форме) и являются решением нашего уравнения. Найдём показательную и алгебраическую формы этих чисел:
![]() ,
,
![]() ,
,
![]() –
показательная форма.
–
показательная форма.
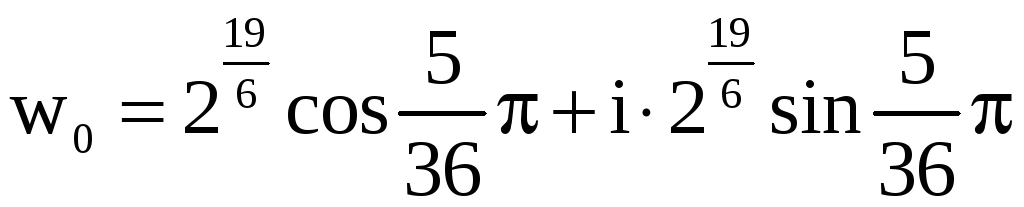 ,
, 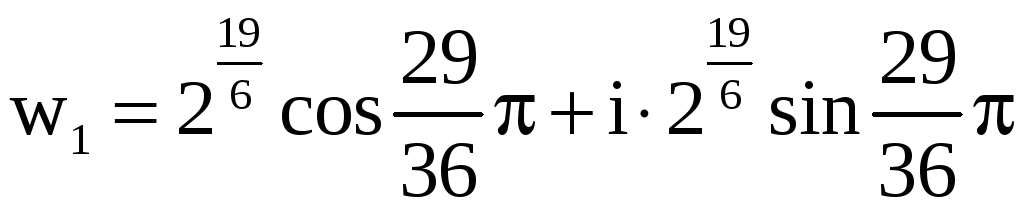 ,
,
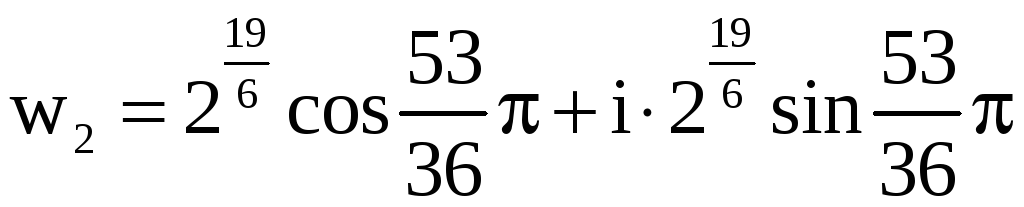 – алгебраическая форма.
– алгебраическая форма.
Пример 5. Решить: а) систему уравнений; б), в) неравенства (геометрически):
а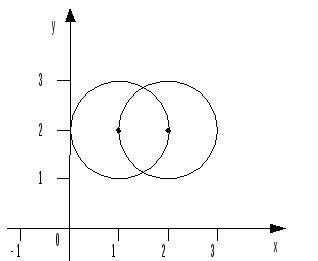 )
)
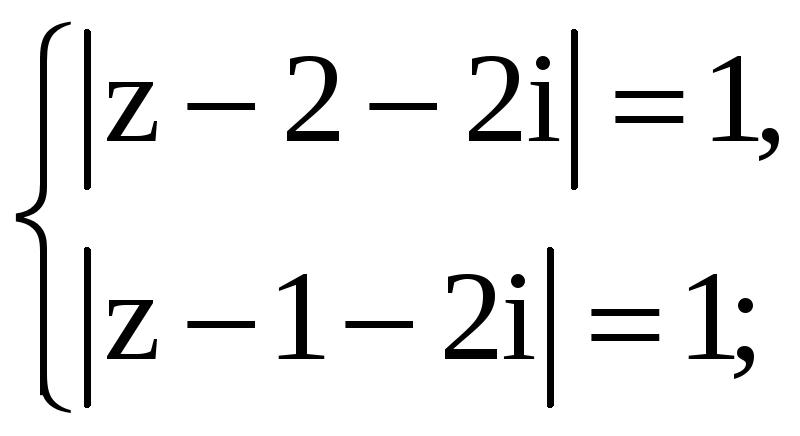
б)
![]() ;
;
в)
![]() .
.
