
II. Введение в анализ
1. Предел числовой последовательности
Числовой
последовательностью
называют правило, по которому каждому
натуральному числу
![]() ставится в соответствие действительное
(комплексное) число
ставится в соответствие действительное
(комплексное) число
![]()
![]() .
Последовательность обозначают символом
.
Последовательность обозначают символом
![]() (
(![]() ).
Можно сказать, что последовательность
является функцией
).
Можно сказать, что последовательность
является функцией
![]() (
(![]() ).
Очевидным образом определяются сумма,
произведение, частное двух
последовательностей. В этом разделе мы
будем иметь дело лишь с последовательностями
действительных чисел.
).
Очевидным образом определяются сумма,
произведение, частное двух
последовательностей. В этом разделе мы
будем иметь дело лишь с последовательностями
действительных чисел.
Число
![]() называется пределом
последовательности
называется пределом
последовательности
![]() если для любого
если для любого
![]() найдётся номер
найдётся номер
![]() такой, что для любого
такой, что для любого
![]() выполняется неравенство
выполняется неравенство
![]() .
При этом пишут
.
При этом пишут
![]() или
или
![]() и говорят, что последовательность
и говорят, что последовательность
![]() сходится к числу
сходится к числу
![]() .
.
Если
![]() ,
,
![]() ,
то: 1)
,
то: 1)
![]() ;
;
2)
![]() ; 3)
; 3)
![]() ;
;
4)
![]() при (
при (![]() ).
).
Пример 1.
Дана последовательность
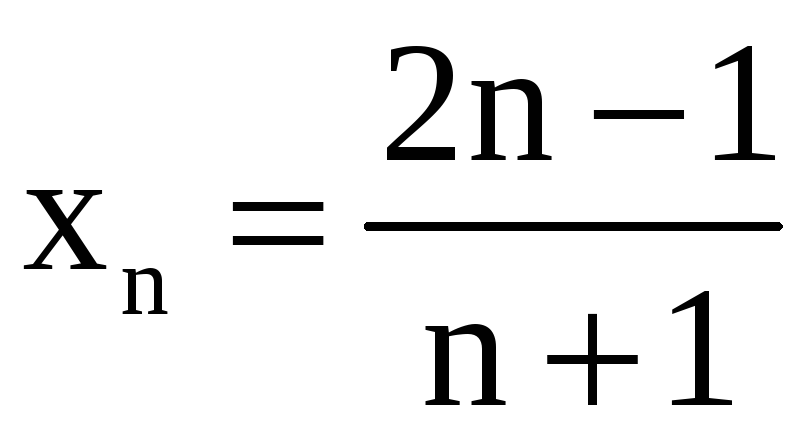 . Найдите:
а)
. Найдите:
а) ![]() ;
б)
;
б) ![]() такое, что для всех
такое, что для всех
![]() выполняется неравенство
выполняется неравенство
![]() .
.
Решение.
а) Имеем
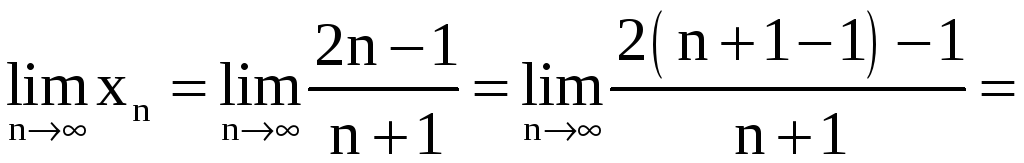
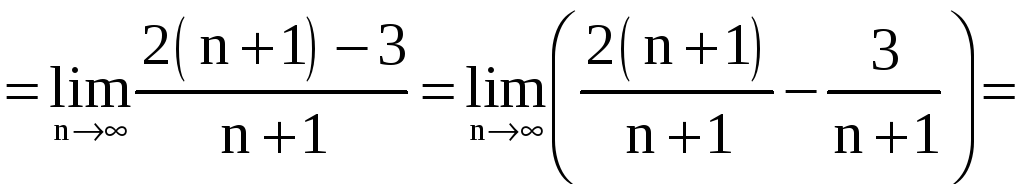
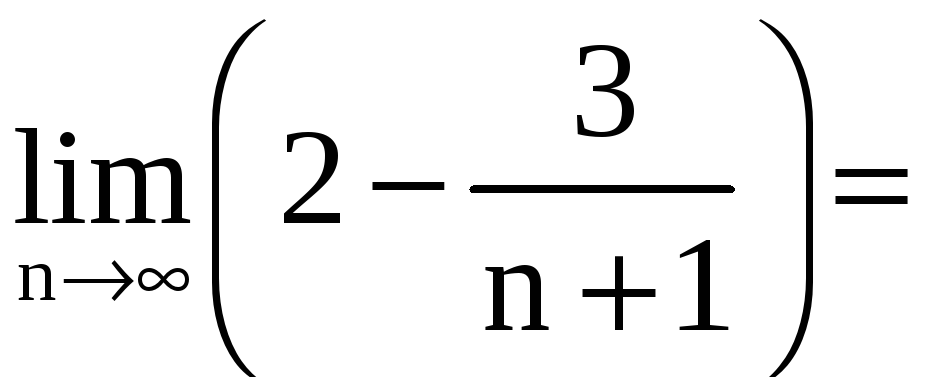
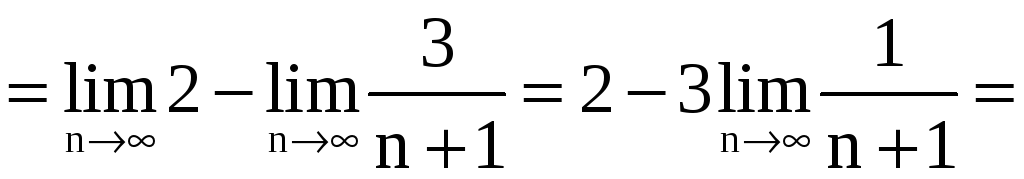
![]() .
.
б)
Найдём требуемое
![]() .
Из проделанных выше выкладок следует,
что
.
Из проделанных выше выкладок следует,
что
![]() должно быть подобрано так, чтобы для
всех
должно быть подобрано так, чтобы для
всех
![]()
 или
или
 ;
;
отсюда
следует
![]() ,
,
![]() .
Следовательно, можно взять
.
Следовательно, можно взять
![]() .
.
Последовательность
![]() называется бесконечно
малой, если
называется бесконечно
малой, если
![]() .
.
Последовательность
![]() называется бесконечно
большой,
если для любого
называется бесконечно
большой,
если для любого
![]() найдётся номер n0
такой, что для любого
найдётся номер n0
такой, что для любого
![]() справедливо неравенство
справедливо неравенство
![]() ;
записывается это так:
;
записывается это так:
![]() .
Если при этом
.
Если при этом
![]() ,
начиная с некоторого номера, сохраняет
положительный (отрицательный) знак, то
пишут
,
начиная с некоторого номера, сохраняет
положительный (отрицательный) знак, то
пишут
![]() (
(![]() )
.
)
.
Важную
роль играет последовательность
 Доказывается, что эта последовательность
сходится, и ее предел обозначается
буквой е; е
Доказывается, что эта последовательность
сходится, и ее предел обозначается
буквой е; е
![]() 2,718.
2,718.
2. Элементарные функции
К элементарным функциям относятся:
1) простейшие
элементарные функции: постоянная с,
степенная
![]() ,
показательная
,
показательная
![]() ,
логарифмическая
,
логарифмическая
![]() ,
тригонометрическая
,
тригонометрическая
![]() ,
обратные тригонометрические
,
обратные тригонометрические
![]() ;
;
2) все функции, получающиеся из простейших элементарных функций путем применения конечного числа следующих четырех операций: сложение, умножение, деление, суперпозиция функций (сложная функция).
Пример 2. В класс элементарных функций попадают:
а)
многочлен; б) рациональная дробь
(отношение двух многочленов); в) ![]() ,
так как
,
так как
![]() ;
г)
;
г) 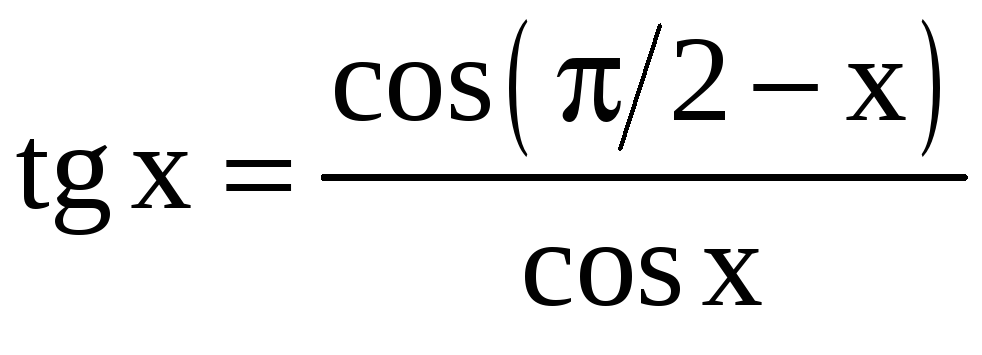 ;
д)
;
д) ![]() ,
так как
,
так как
 и множество других.
и множество других.
3. Предел функции
Пусть функция
![]() определена во всех точках интервала
определена во всех точках интервала
![]() ,
за исключением, быть может, точки
,
за исключением, быть может, точки
![]() .
Число А называется пределом функции
.
Число А называется пределом функции
![]() в точке
в точке
![]() ,
если для любого
,
если для любого
![]() существует число
существует число
![]() такое, что для любого x, удовлетворяющего
неравенству
такое, что для любого x, удовлетворяющего
неравенству
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() ,
при этом пишут
,
при этом пишут
![]() .
Можно дать другое, равносильное
приведенному, определение: число A
называется пределом функции
.
Можно дать другое, равносильное
приведенному, определение: число A
называется пределом функции
![]() в точке x0,
если для любой последовательности чисел
в точке x0,
если для любой последовательности чисел
![]() ,
сходящейся к
,
сходящейся к
![]() ,
,
![]()
![]() .
.
Если
![]() определена в интервале
определена в интервале
![]() ,
то число A называется пределом
,
то число A называется пределом
![]() при
при
![]() ,
если для любого
,
если для любого
![]() существует число
существует число
![]() ,
такое, что неравенство
,
такое, что неравенство
![]() влечет за собой неравенство
влечет за собой неравенство
![]() .
При этом пишут
.
При этом пишут
![]() или
или
![]() .
Аналогично определяется
.
Аналогично определяется
![]() .
.
Число A
называют пределом функции
![]() в точке
в точке
![]() слева (справа) и пишут
слева (справа) и пишут
![]() или
или
![]()
![]() ,
или
,
или
![]() ,
если для любого
,
если для любого
![]() найдется
найдется
![]() такое, что для всех
такое, что для всех
![]() (для всех
(для всех
![]() )
справедливо неравенство
)
справедливо неравенство
![]() .
Число A
является пределом
.
Число A
является пределом
![]() в точке
в точке
![]() ,
если совпадают пределы
,
если совпадают пределы
![]() в этой точке слева и справа:
в этой точке слева и справа:
![]() .
.
Если
функция
![]() определена в интервале
определена в интервале
![]() (в интервале
(в интервале
![]() )
и для любого M
существует
)
и для любого M
существует
![]() такое, что для любого
такое, что для любого
![]() (для любого
(для любого
![]() справедливо неравенство
справедливо неравенство
![]() ,
то говорят, что левый (правый) предел
функции
,
то говорят, что левый (правый) предел
функции
![]() в точке
в точке
![]() равен
равен
![]() ,
и при этом пишут
,
и при этом пишут
![]() или
или
![]()
![]() или
или
![]() Аналогично определяются
Аналогично определяются
![]() и
и
![]() .
.
Предел
функции обладает теми же свойствами,
что и предел последовательности: если
![]() ,
,
![]() ,
то
,
то
(последнее
при
![]() ).
То же верно для односторонних пределов.
).
То же верно для односторонних пределов.
Пример 3.
Доказать, что
![]() .
По данному
.
По данному
![]() найти
найти
![]() такое, что из неравенства
такое, что из неравенства
![]() следует
следует
![]() .
.
Решение.
Пусть
![]() произвольно. Неравенство
произвольно. Неравенство
![]()
![]()
![]() равносильно
неравенству
равносильно
неравенству
![]() .
Поэтому, если по данному
.
Поэтому, если по данному
![]() взять
взять
![]() ,
то из неравенства
,
то из неравенства
![]() будет следовать неравенство
будет следовать неравенство
![]() а это и означает, что
а это и означает, что
![]() .
В частности, для
.
В частности, для
![]() достаточно взять
достаточно взять
![]() .
.
Пример 4. Найти пределы:
а)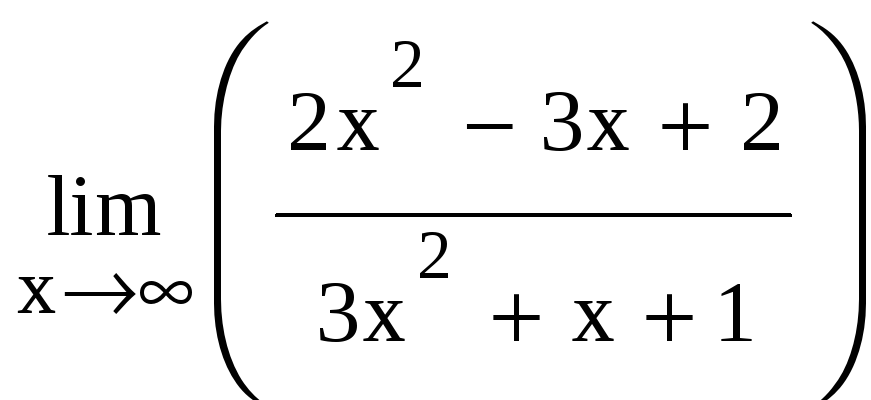 ,
б)
,
б) ,
в)
,
в)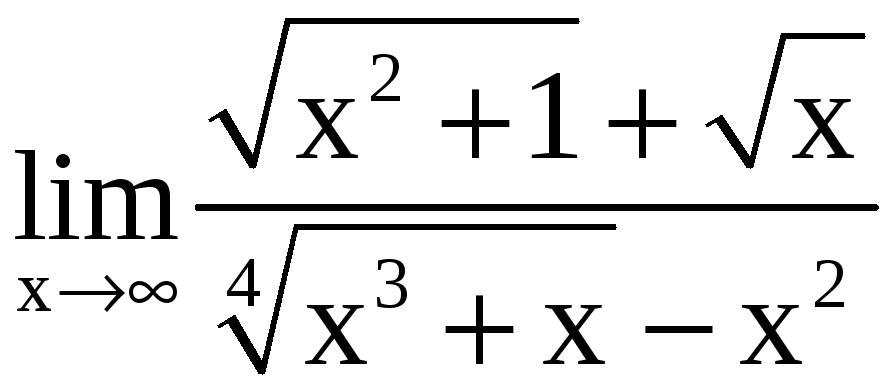 .
.
Решение.
а)
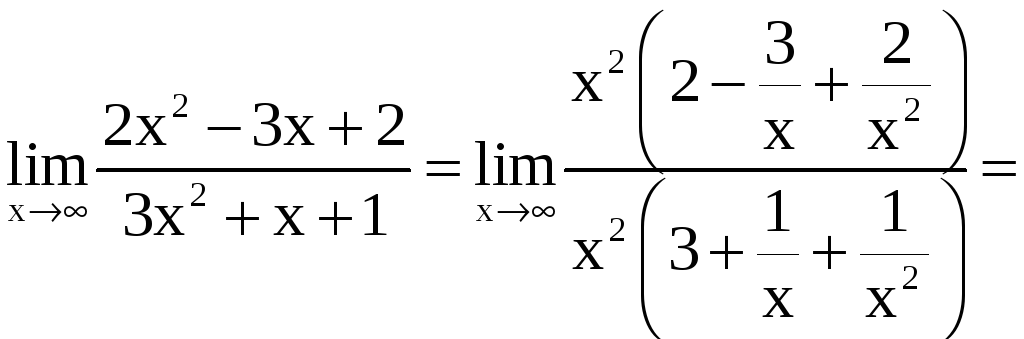

 ;
;
б)


в)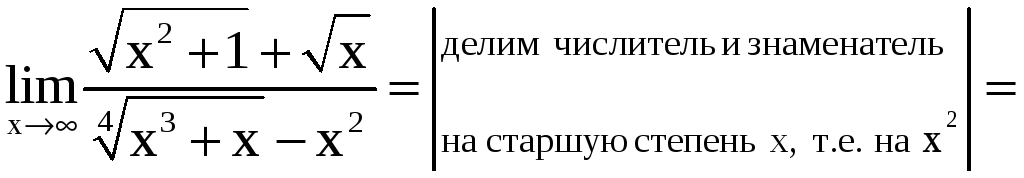
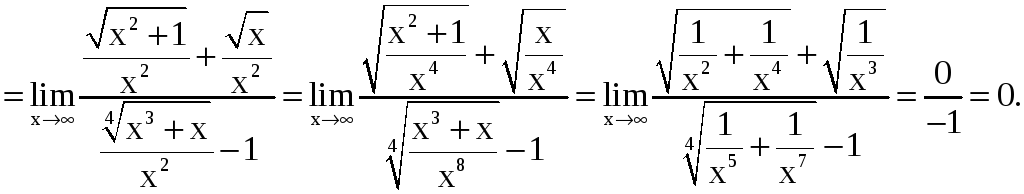
Пример 5. Вычислить:
а)
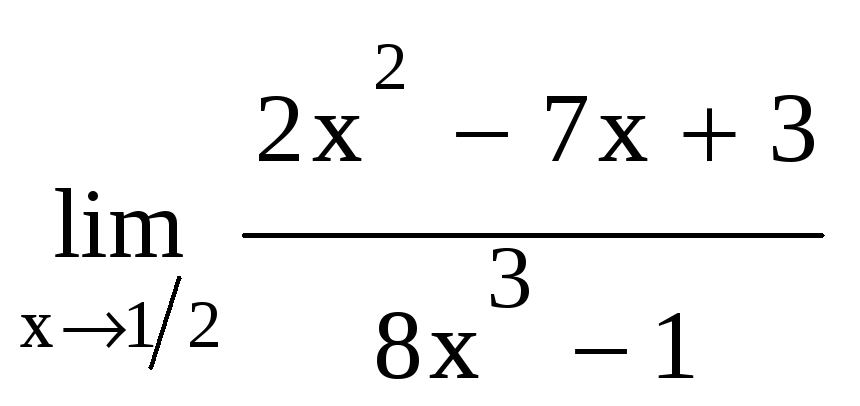 б)
б)

Решение. а)
При подстановке
 в числитель и знаменатель они обращаются
в нуль.
в числитель и знаменатель они обращаются
в нуль.
Следовательно, мы
имеем неопределенность вида
![]()
Разложим числитель и знаменатель на множители и перейдем к пределу



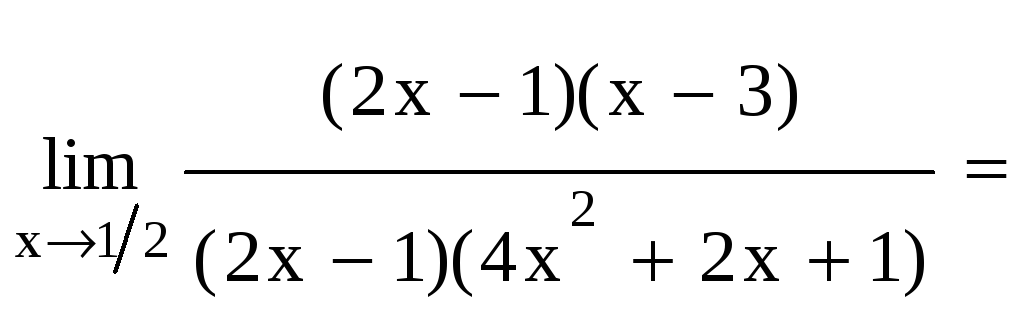

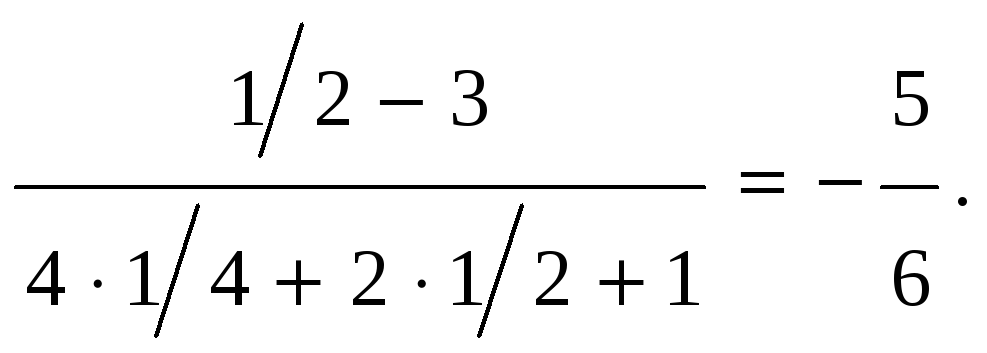
б)
В этом примере
имеем неопределенность вида
![]() .
Умножим числитель и знаменатель на
произведение
.
Умножим числитель и знаменатель на
произведение
![]() ,
получим
,
получим

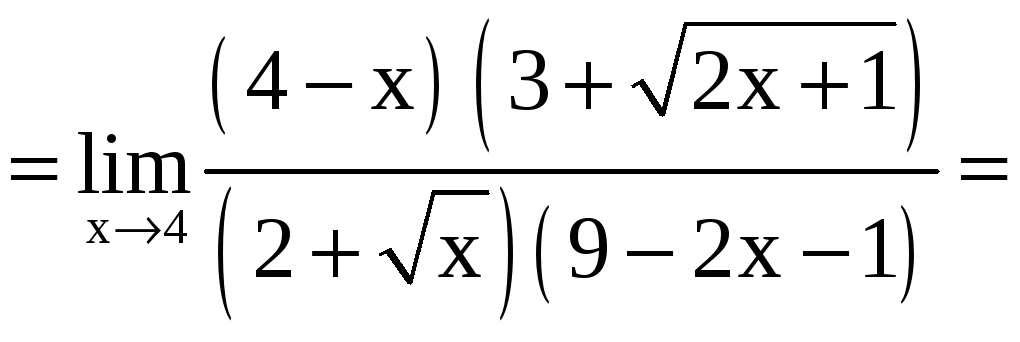
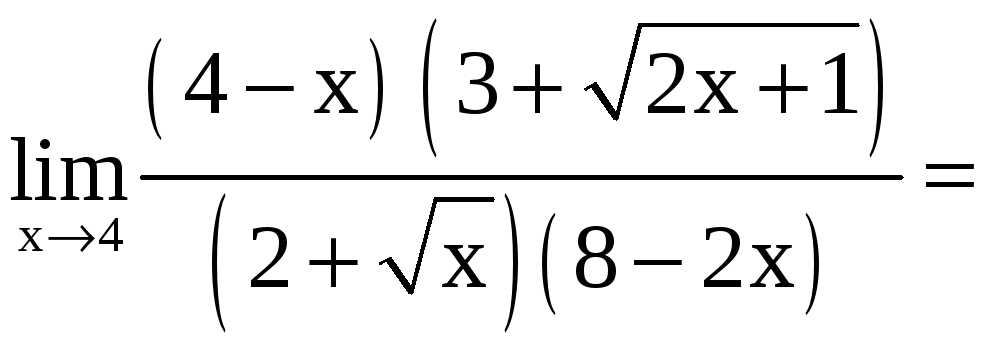
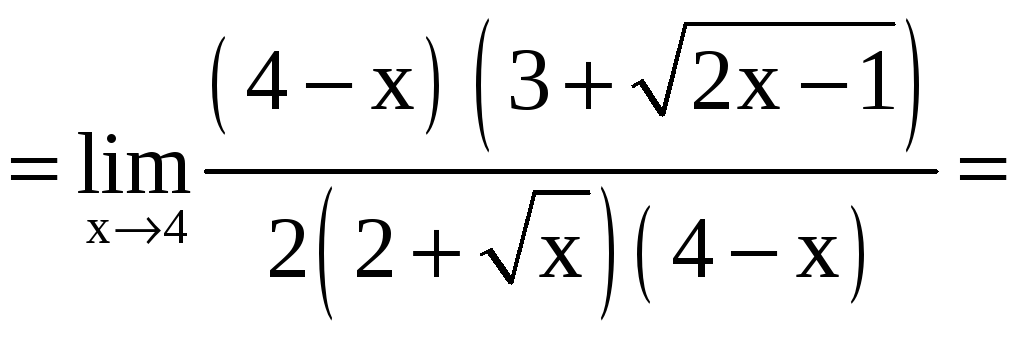

![]()
![]() .
.
Пример 6.
![]() .
.
Решение. Имеем
неопределенность вида![]() .
.
![]()
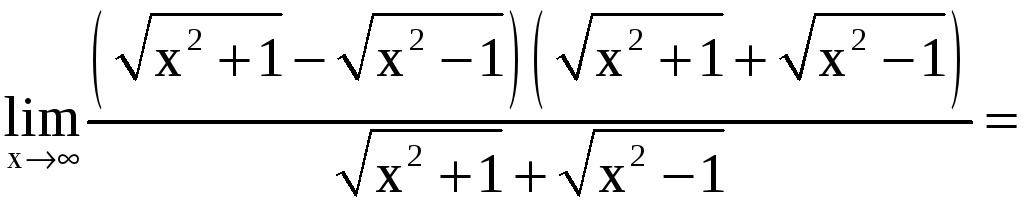
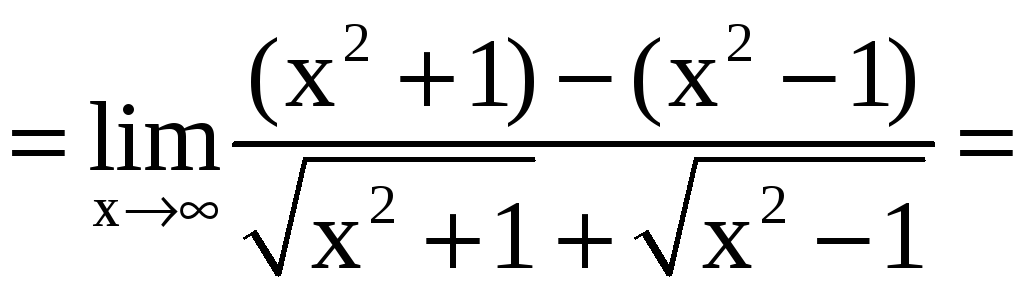
 .
.
Имеют место равенства
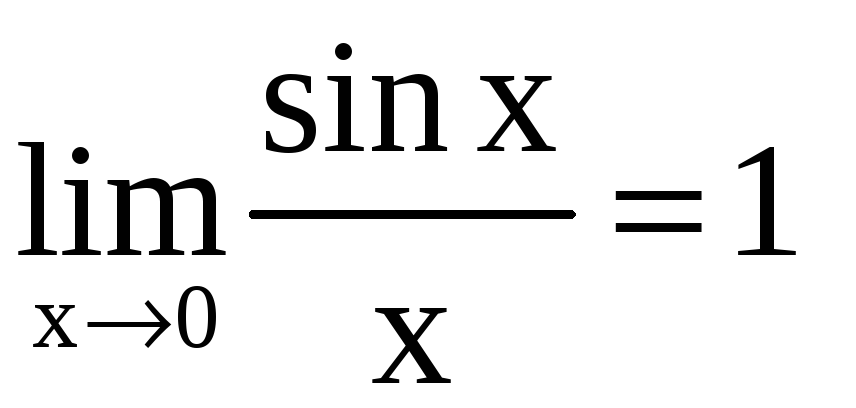 ,
,
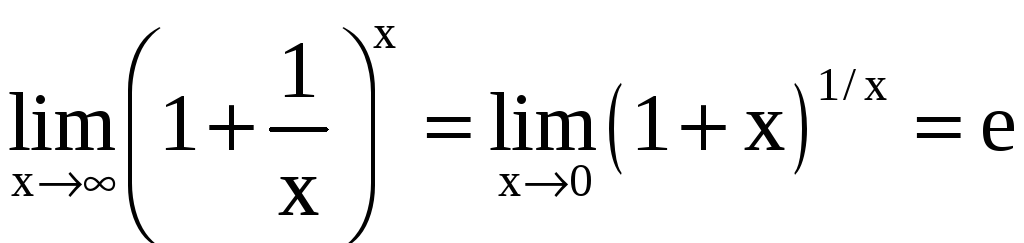 ,
,
называемые первым и вторым замечательными пределами.
Пример 7. Найти:
а)
 ; б)
; б)
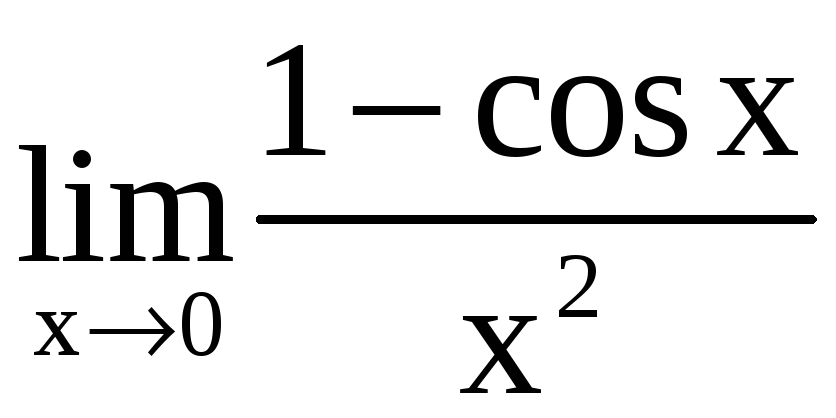 ;
в)
;
в)
 .
.
Решение. а) Применяем первый замечательный предел:
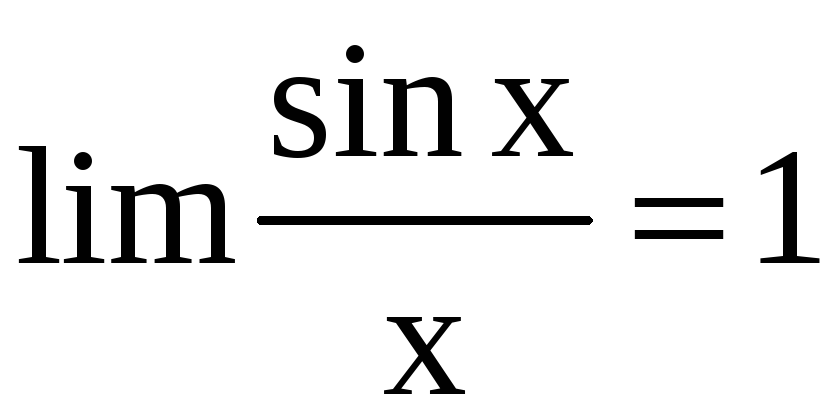 .
.
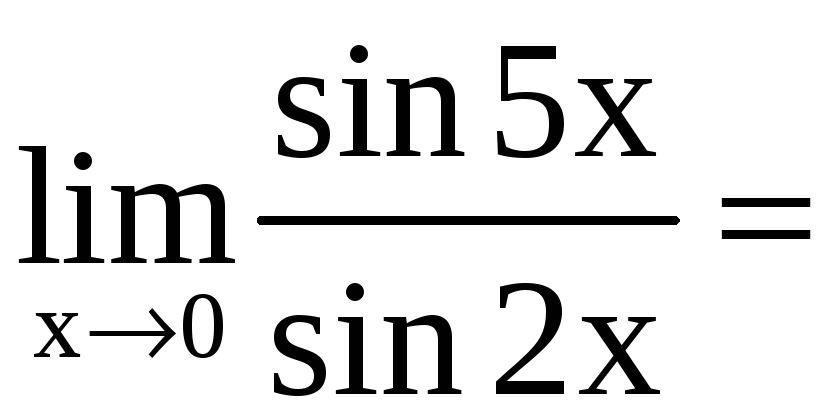

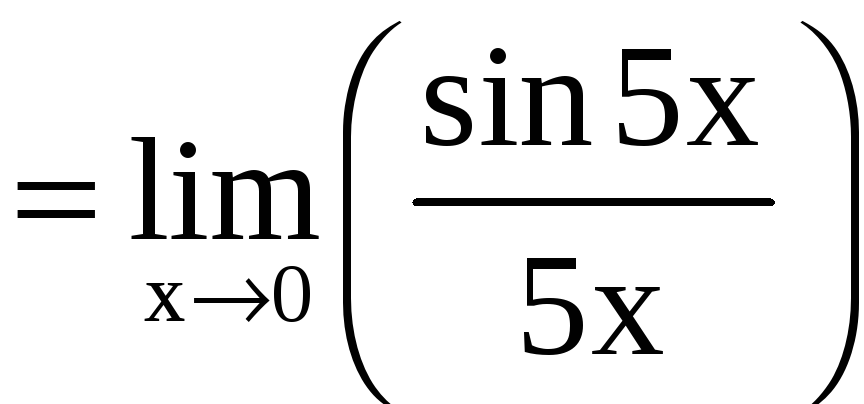

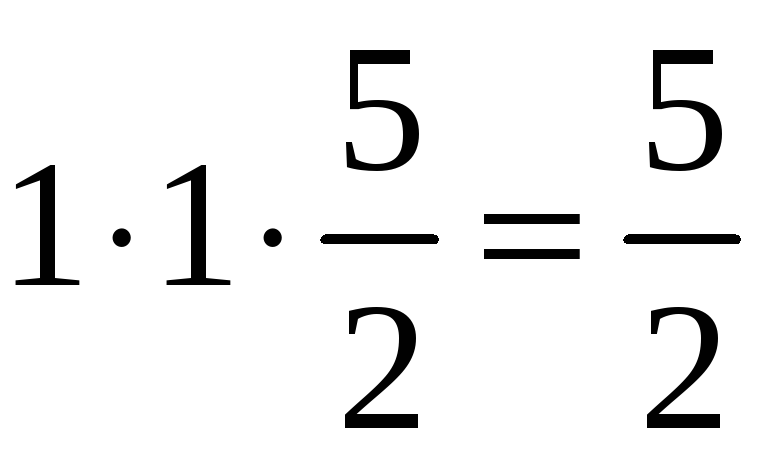 .
.
б)


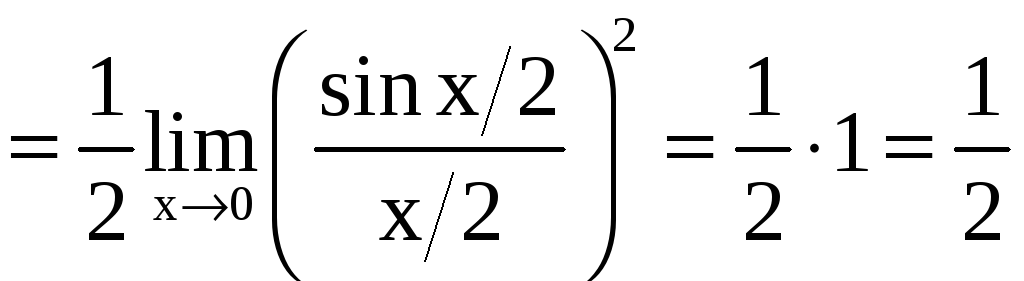 .
.![]()
в)
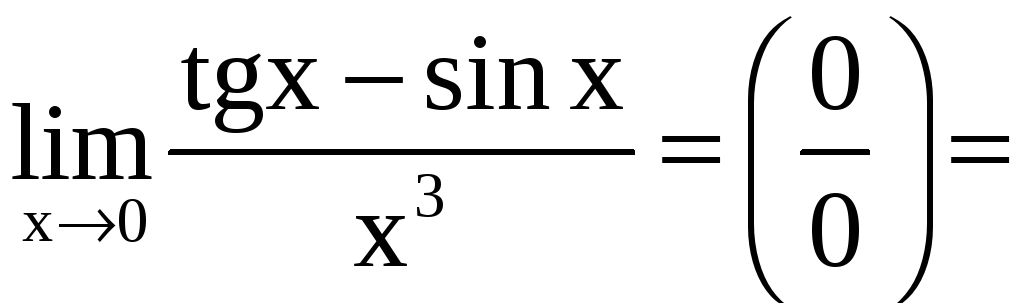
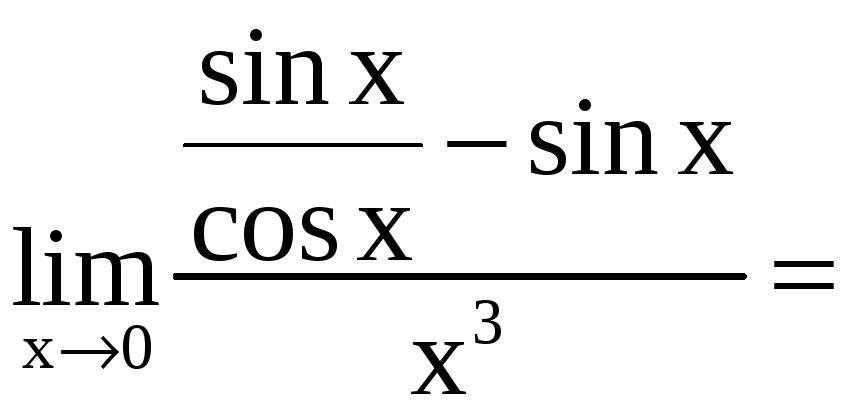
=
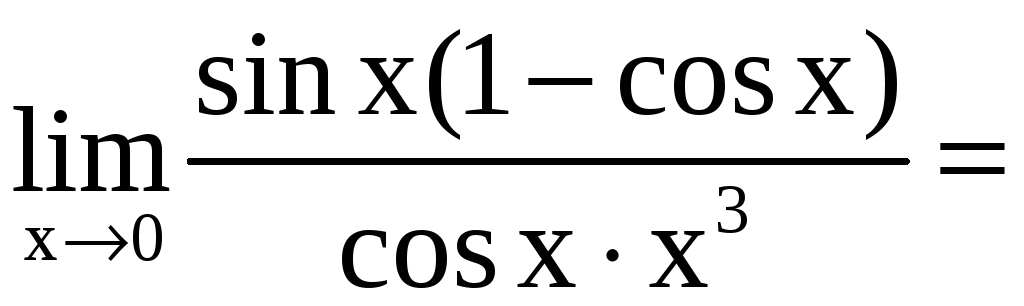

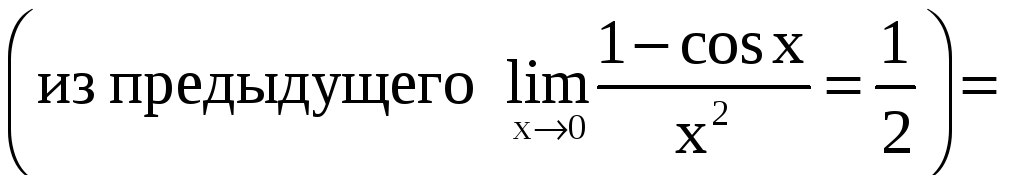
 .
.
Пример 8. Найти:
а)
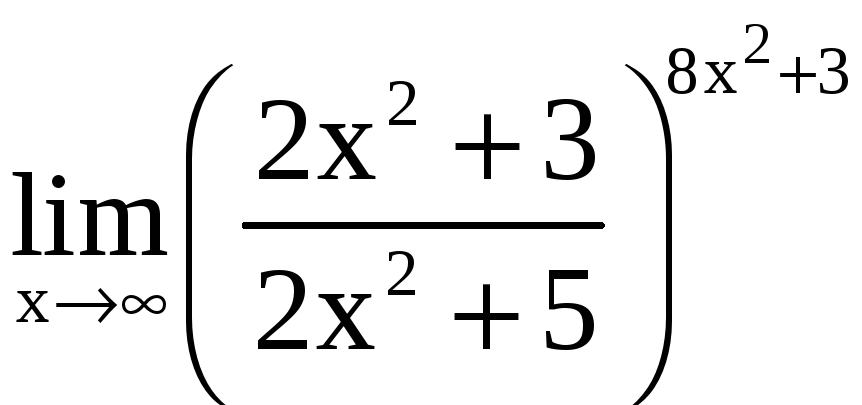 ; б)
; б)
![]() .
.
Решение.
а) 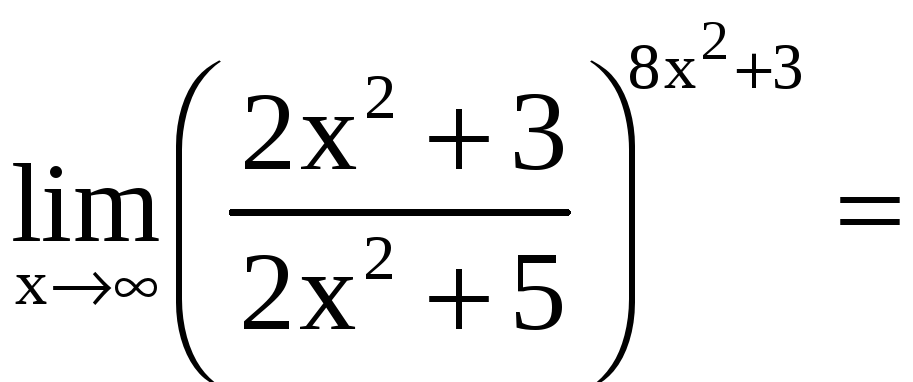
 .
.
В основании прибавим и вычтем единицу

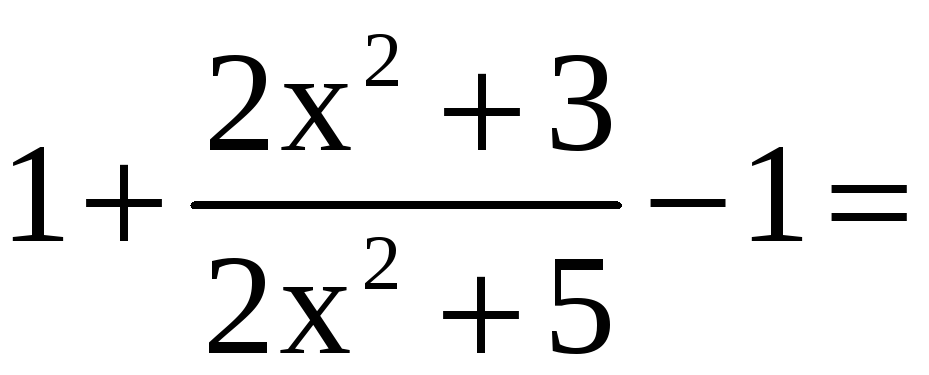
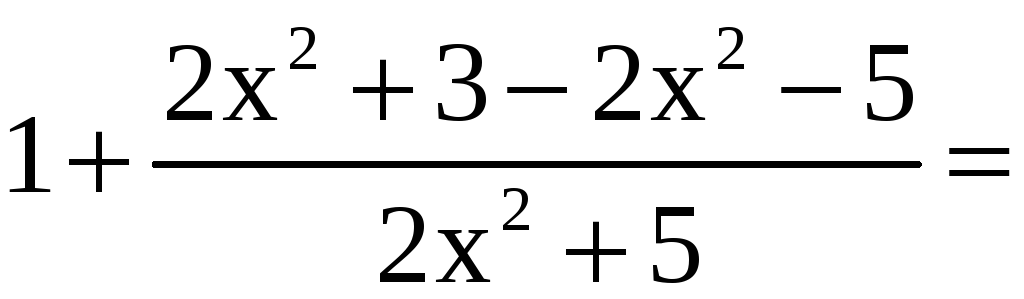
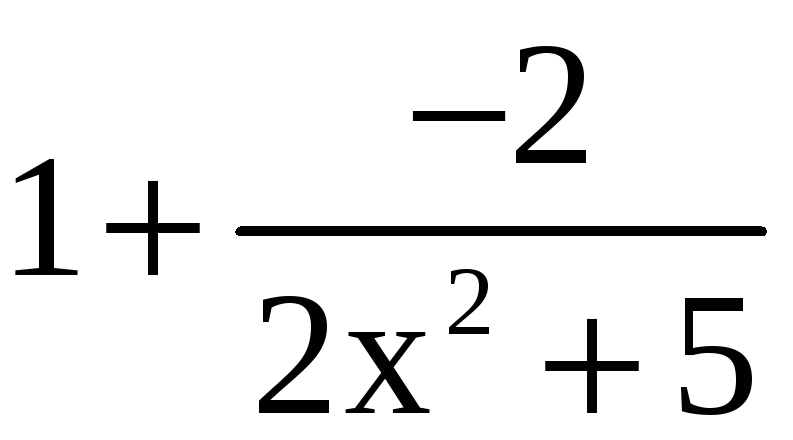 .
.
Тогда
![]()
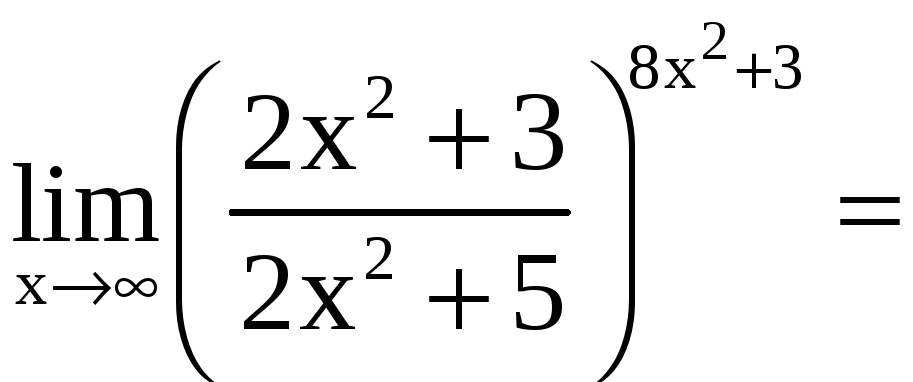

![]()

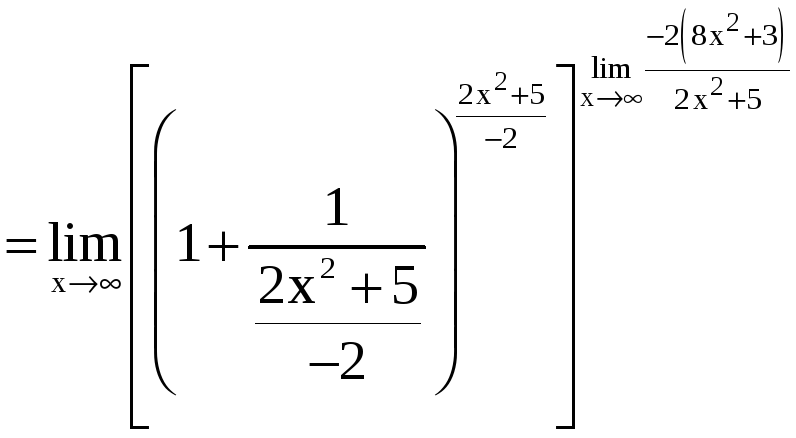 .
.
Вычисляем
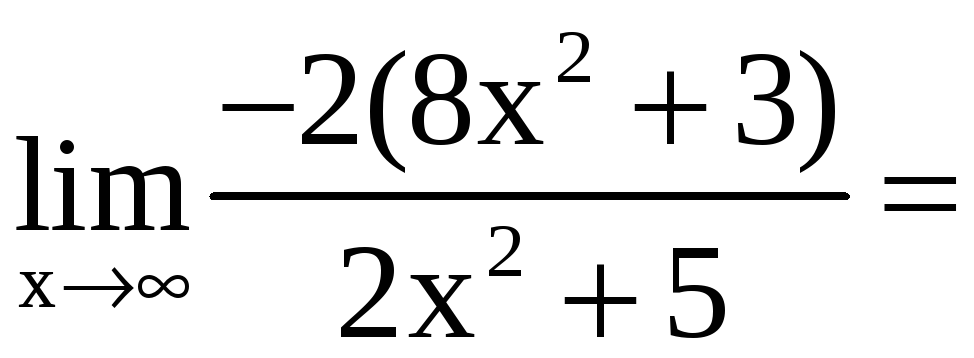
 =
=
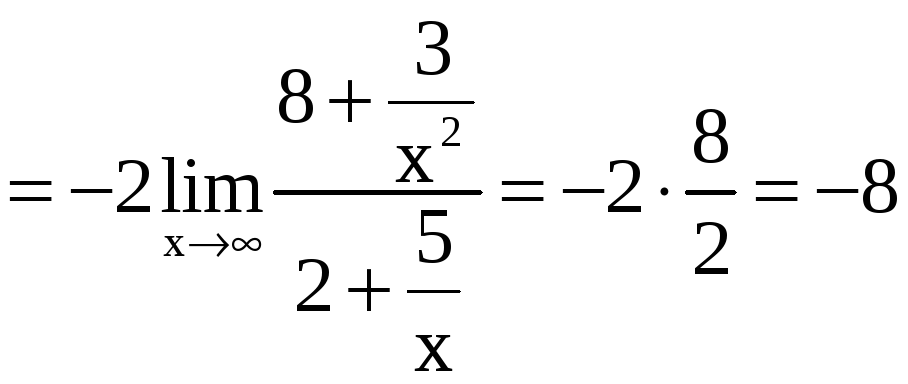 .
.
Тогда

б)
![]()


![]()
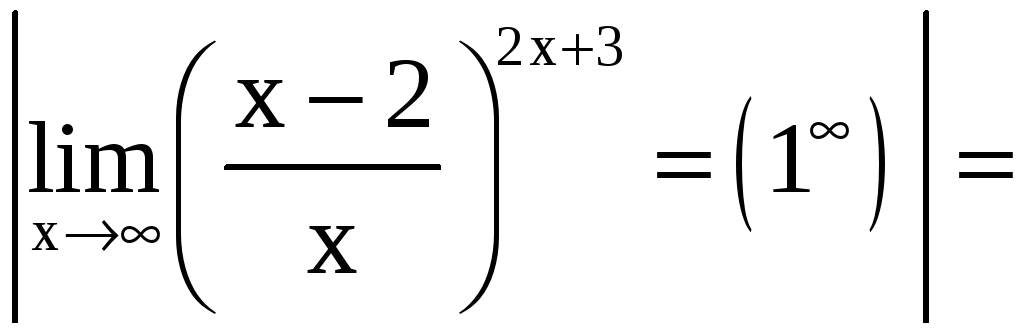
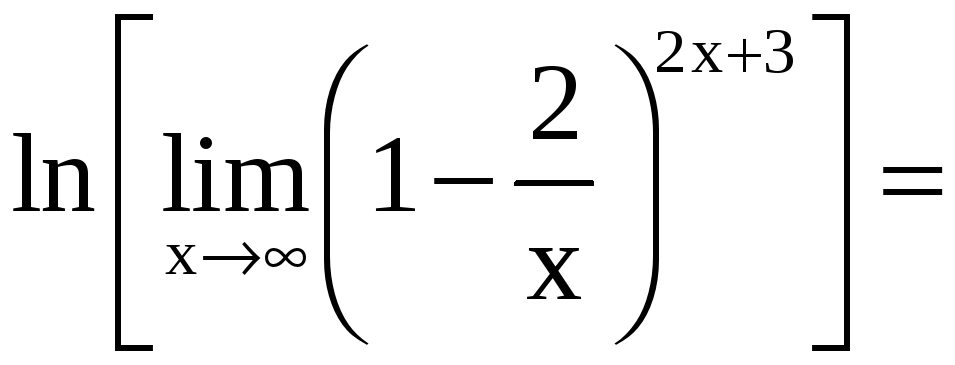


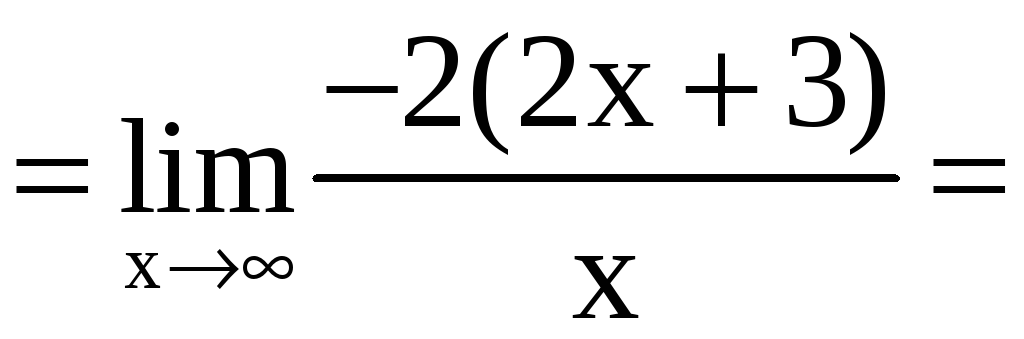
 .
.
Тогда
 .
.
в)
![]()
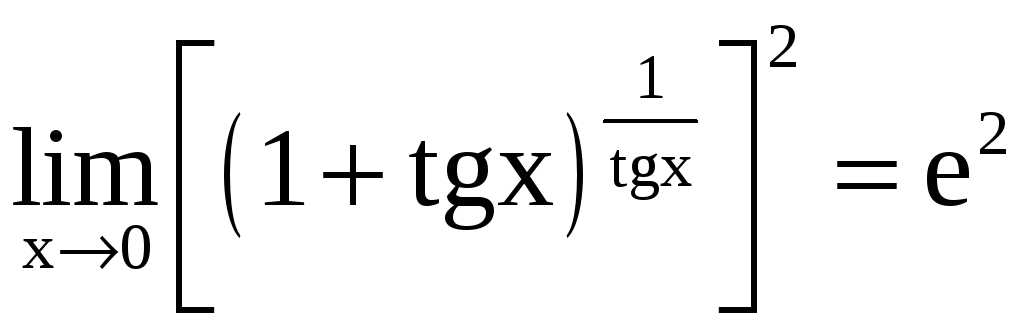 .
.
