2. Статический расчет сложноконсольной балки

Многопролетная статически определимая балка представляет собой комбинированную систему, состоящую из нескольких однопролетных балок, соединенных таким образом, что в местах их соединения в расчетной схеме возможна постановка шарниров.

На рис.9 представлена расчетная схема статически опреде­лимой многопролетной балки.

Рис. 9

Для геометрической неизменяемости и статистической оп­ределимости сложноконсольной балки число шарниров, введен­ных в пролеты, должно удовлетворять условию:

Ш=С₀ -3. (4)

Из этого следует, что при крайних шарнирных опорах чис­ло шарниров в пролетах должно быть равно числу промежуточ­ных опор. Условие (4) является необходимым. Для выполнения достаточного условия неизменяемости балки

размещение шарни­ров в пролетах должно подчиняться следующим правилам:

• в каждом пролете должно быть не более двух шарниров;

• пролеты с двумя шарнирами должны чередоваться с про­летами без шарниров;

• пролеты с одним шарниром могут следовать один за дру­гим при условии, что один пролет остается без шарнира.

Оптимизация расчетной схемы сложноконсольной балки может быть реализована расположением промежуточных шарни­ров таким образом, чтобы наибольшие изгибающие моменты в пролетах и над опорами были равны между собой по модулю или находились в определенном соотношении.

Расчет сложноконсольной балки удобно производить путем представления ее расчетной схемы в виде «этажной» системы, в которой выделяются основные неизменяемые элементы и под­весные, опирающиеся на основные. Начинать расчет следует с подвесных элементов. Определив их опорные реакции, переходят к основным элементам, добавляя к нагрузкам, действующим на эти элементы, давления от верхних подвесных элементов. Эпюры усилий М и Q удобно строить для каждого элемента (этажа) от­дельно, объединяя их впоследствии на одном чертеже. Техника расчета показана на рис.10.

Порядок расчета «этажей» следует из структуры «этажной», схемы. Он может быть:

II → III → IV, I,

или II → I, III → IV

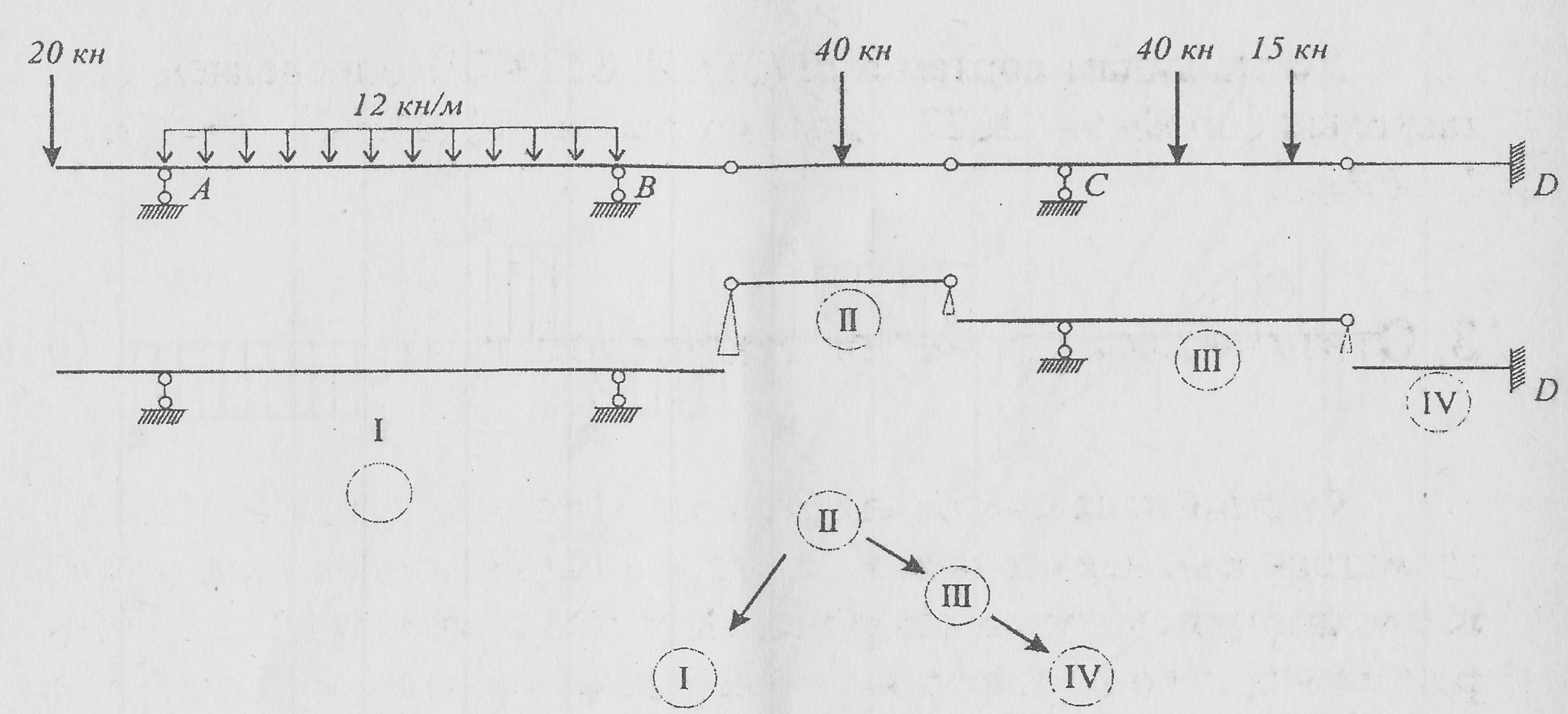
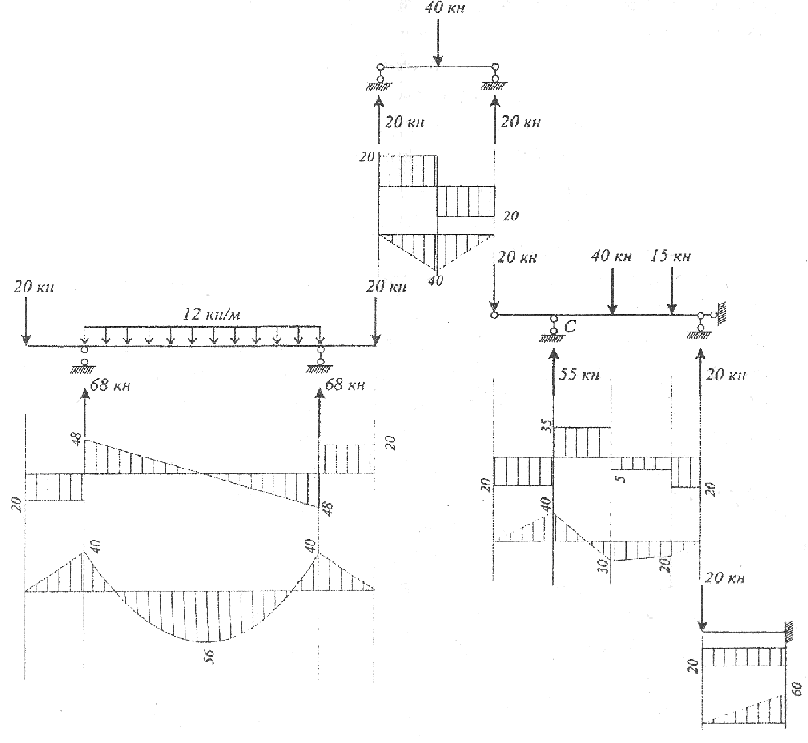
Рис. 10

На рис.11 представлены эпюры MhQb данной балке.

Рис. 11

Опасным сечением является сечение 8, где М=6ОkНм. Под­бираем двутавровый профиль из условия прочности по нормаль­ным напряжениям при изгибе балок:

По таблицам сортамента (ГОСТ 8239-72) определяем дву­тавровый профиль №27, для которого W_x=S71cм³, F=40,2cм²,I_х=5010см⁴.

3. Статический расчет плоской фермы

Фермой называется стержневая система, которая остается геометрически неизменяемой после условной замены в расчетной схеме жестких узлов шарнирами. Нагрузка в расчетной схеме пе­редается только в узлах в виде сосредоточенных сил. Поэтому в стержнях фермы возникают только продольные усилия. Практи­чески важной является проблема приведения реальных дейст­вующих нагрузок к сосредоточенным силам, приложенным в уз­лах фермы или «сбора нагрузок» на ферму. В задании к данной курсовой работе рассматриваются три вида нагрузок:

• постоянная (вес конструкций, оборудования и т.д.), на­правленная вертикально;

• временная снеговая (вес снегового покрова), направлен­ная вертикально;

• временная ветровая, направленная по нормали к поверх­ности,

Данные об этих нагрузках обычно определяются в задании на проектирование и по СНиП «Нагрузки и воздействия» и пред­ставляются в виде распределенных усилий, отнесенных к едини­це площади.

На рис.12 представлена расчетная схема фермы, приведены ее размеры и данные по действующим нагрузкам.

d=2м (размер панели и высота фермы)

1=6м (расстояние между фермами)

q_n=4kH/м² (интенсивность постоянной нагрузки)

q_c=lkH/м² (интенсивность снеговой нагрузки)

q_e=0,6kH/м² (интенсивность ветровой нагрузки)

Техника сбора нагрузок представлена на рис.13 . В этой связи имеем следующие расчетные схемы для данной фермы (рис. 14).

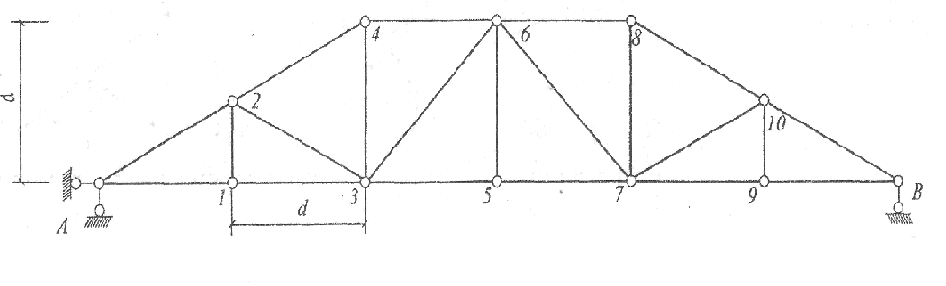
Рис. 12

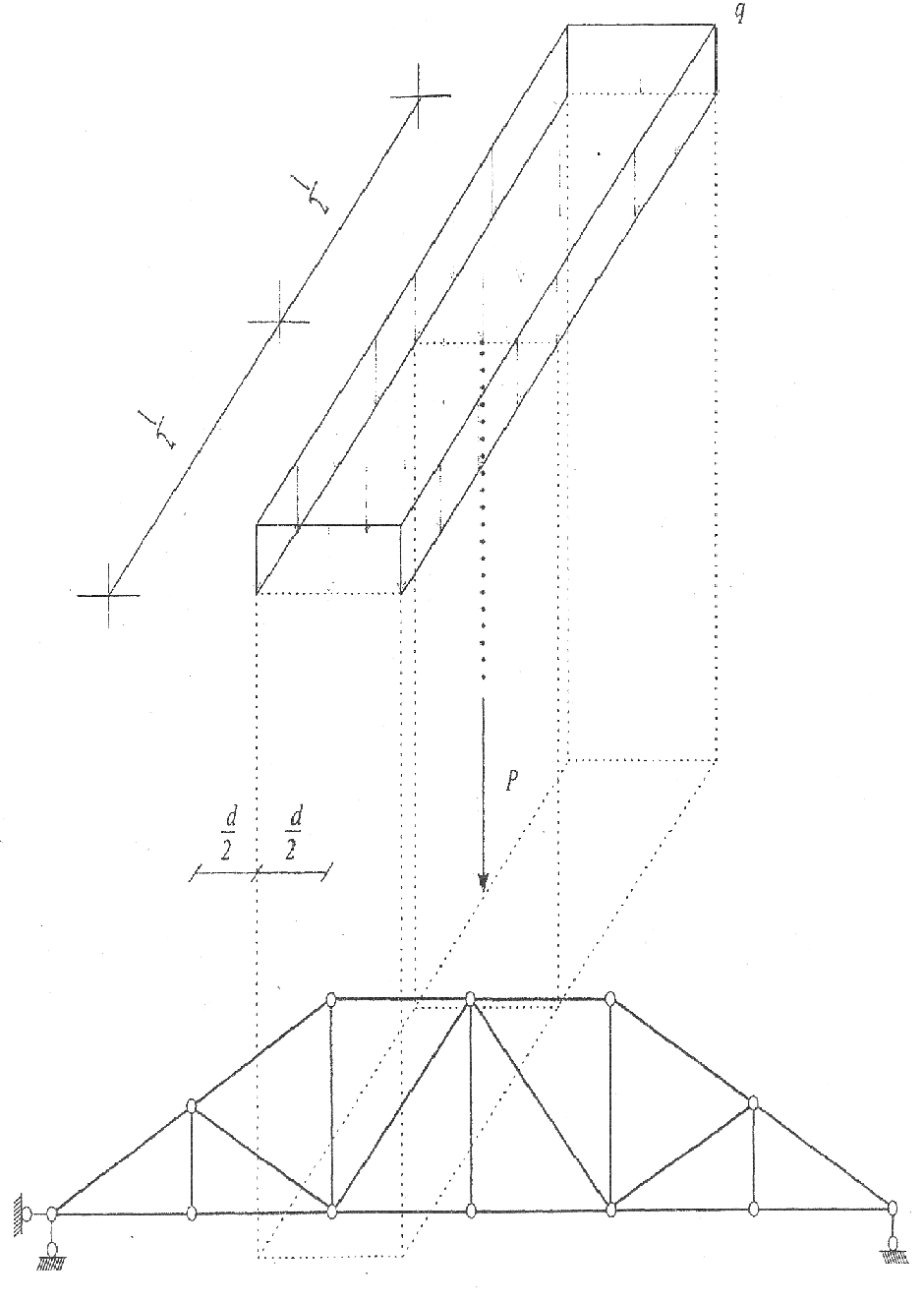
Рис. 13

а) расчет на действие постоянной нагрузки;

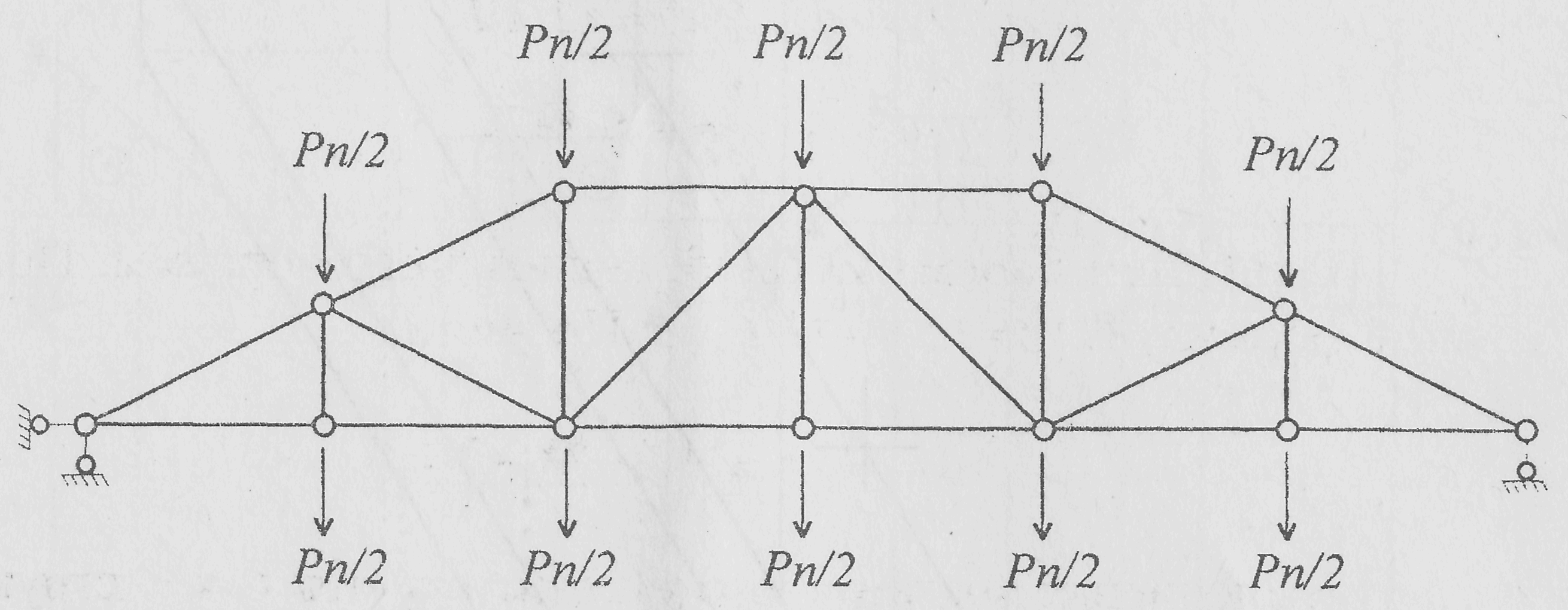
Р_п = q_n∙l∙d = 48kH. Здесь учтено, что постоянная нагруз­ка поровну разделена между узлами верхнего и нижнего пояса;

б) расчет на действие снеговой нагрузки;

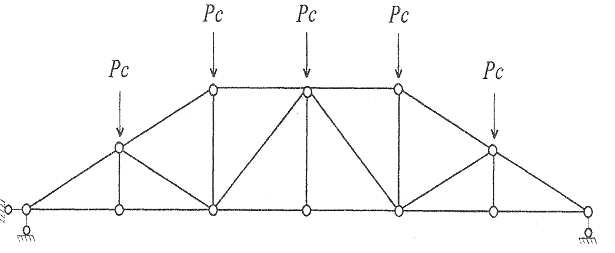
Рс = q_n∙l∙d = 12kH

в) расчет на действие ветровой нагрузки;

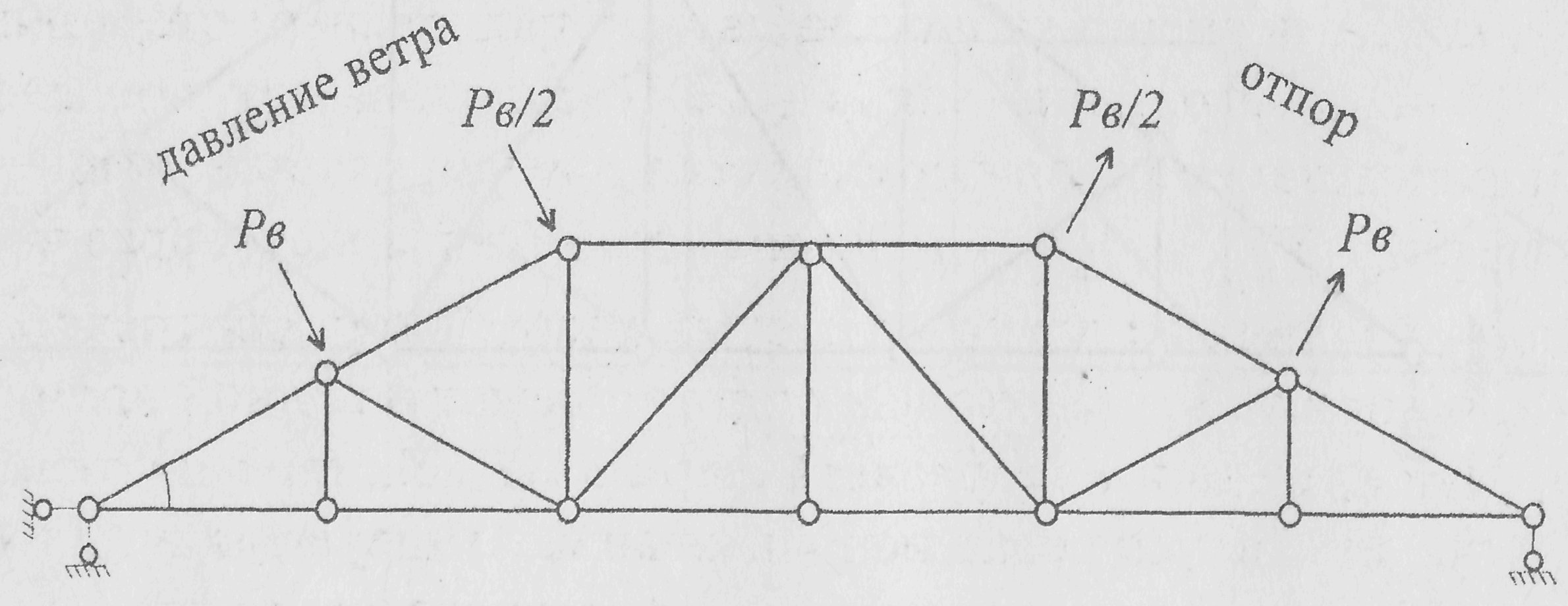
Рис.14

Выполним кинематический анализ данной фермы. Подста­вим в формулу (2) Y=12, C=21, С₀=3. Получим

W = 2∙12 – 21 - 3 = 0.

Выполнение достаточного условия очевидно, т.к. структура фермы организована по принципу диады.

Реакции опор в простых балочных фермах определяются также как в однопролетных балках с помощью уравнений вида

, .

Для проверки реакций опор используем уравнение

.

Аналитический расчет фермы может быть выполнен спо­собами моментной точки, проекций и вырезаний узлов, сущность которых следует из метода сечений. Упомянутые способы опре­деления усилий в стержнях фермы различаются смыслом состав­ляемых уравнений равновесия.

Способ моментной точки (СМТ): сечение пересекает не бо­лее трех стержней фермы, в том числе обязательно тот, в котором определяется усилие; затем составляется уравнение моментов сил, действующих на рассматриваемую часть фермы, относи­тельно точек пересечения двух других стержней (кроме рассчи­тываемого); из этого уравнения определяется искомое усилие.

Если два из рассеченных стержней параллельны, то моментная точка для определения усилия в третьем стержне удаля­ется в бесконечность. В этом случае используется способ проек­ций (СП), в соответствии, с которым составляется уравнение про­екций на ось, перпендикулярную двум параллельным стержням.

Способ вырезания узлов (СВУ) предполагает последова­тельное вырезание узлов фермы и составление для них уравнений равновесия (∑X = 0; ∑Y = 0). Таким способом целесообразно оп­ределять усилия для двухстержневых узлов, либо для трехстержневых, но при условии, что два стержня лежат на одной прямой.

Ниже, на примере расчета фермы на действие постоянной нагрузки, иллюстрируется использование вышеупомянутых спо­собов для определения усилий в некоторых стержнях фермы.

СМТ.

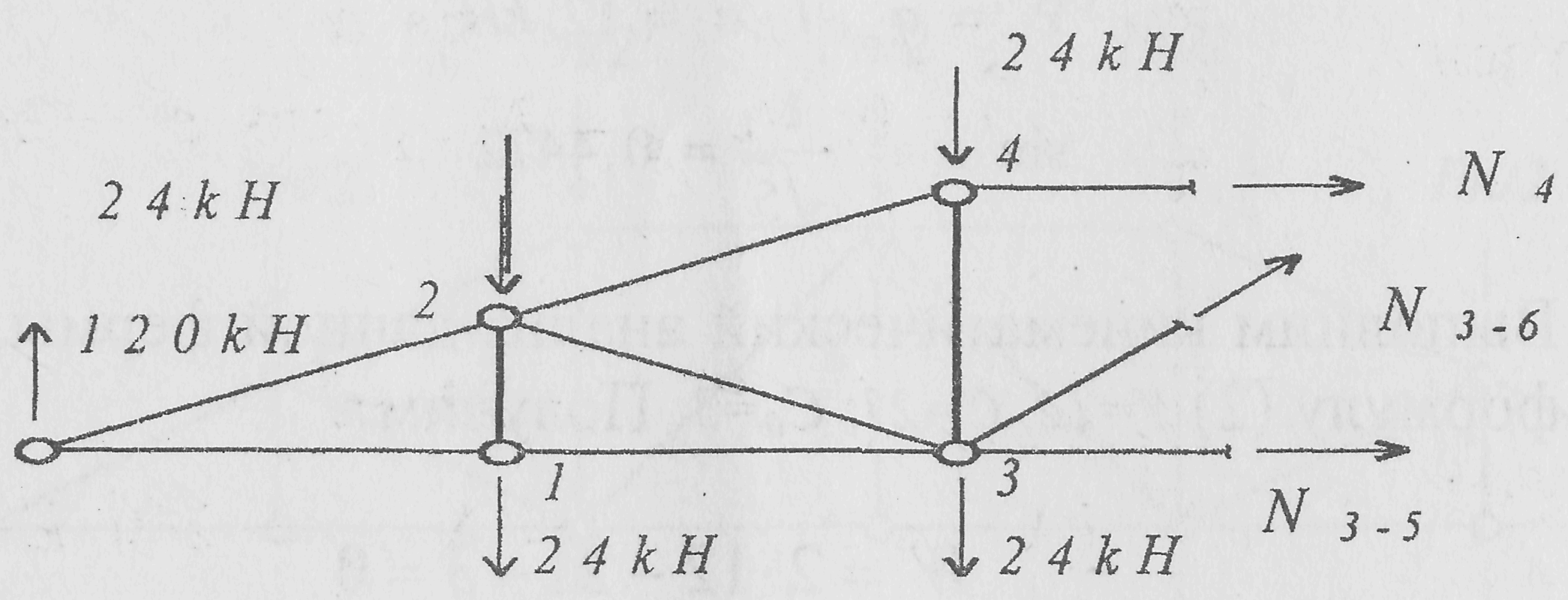
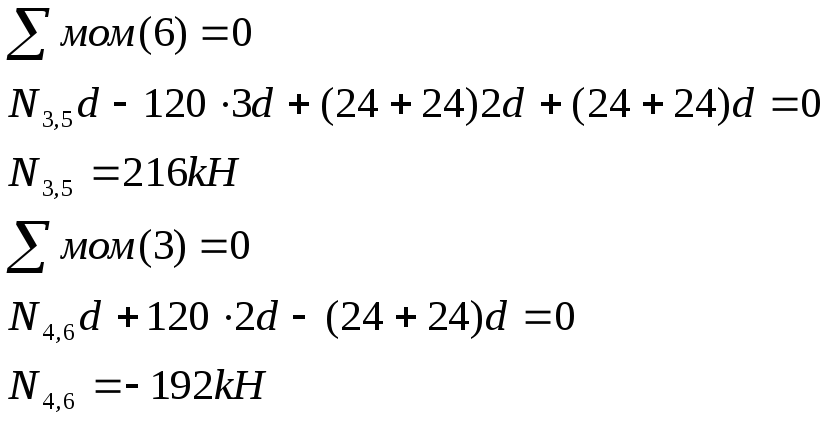
СП.

СВУ.

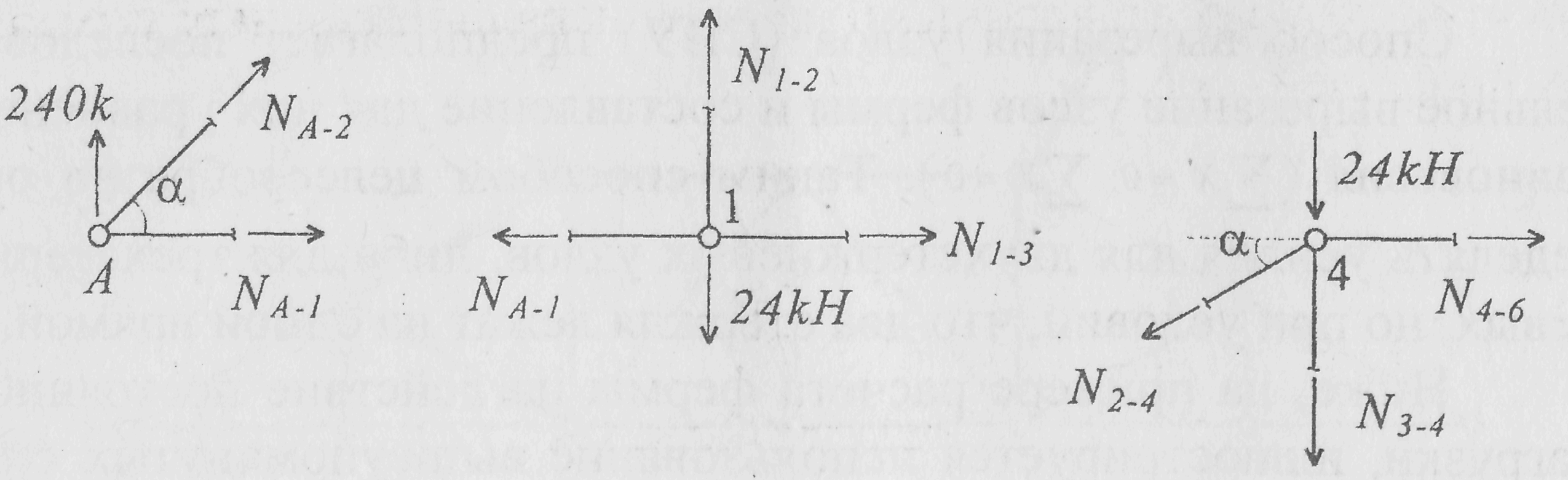
Узел А

Узел 1

Узел 4

Результаты расчета фермы удобно представить в виде табл.1

В табл. 1 усилия от действия снеговой нагрузки представ­лены в двух столбцах: при наличии снеговой нагрузки и при ее отсутствии. Усилия от действия ветровой нагрузки даны с двумя знаками: - верхний знак при напоре ветра слева, нижний при напоре ветра справа.

Расчетное усилие определяется как сумма усилий от дейст­вия постоянной, снеговой и ветровой нагрузок в таком сочетании, которые дает наибольшее по абсолютной величине значение.

По значениям расчетных усилий определяются площади поперечных сечений элементов фермы. Обычно стержни фермы проектируются составленными из двух неравнополочных уголко­вых профилей (рис. 15).

Рис. 15

Проектные значения площади поперечного сечения и но­мер профиля определяются из условий прочности, которые раз­личаются для растянутых и

Таблица 1

Стер­жень	Длина li [м]	[kH]	[kH]	[kH]	[kH]	Профиль	Площадь составного сечения [см2]
1	2	3	4	5	6	1	8	9
А-1	2	240	60	0	±8,88	308,88	75x50x8	18,94
1-3	2	240	60	0	±8,88	308,88	75x50x8	18,94
3-5	2	216	54	0	±2,88	272,88	90x56x6	17,08
5-7	2	216	54	0	±2,88	272,88	90x56x6	17,08
7-9	2	240	60	0	±3,06	303,06	75x50x8	18,94
9.-В	2	240	60	0	±3,06	303,06	75x50x8	18,94
А-2	2,24	-268,34	0	-63,08	±4,29	-335,7	140x90x10	4,44
2-4	2,24	-214,67	0	-53,67	±1,88	-270,2	125x80x10	39,4
4-6	2	-192	0	-48	±2,4	-242,4	100x63x10	31
6-8	2	-192	0	-48	±2,4	-242,4	100x63x10	31
8-10	2,24	-214,67	0	-53,67	±1,88	-270,2	125x80x10	39,4
10-В	2,24	-268,34	0	-63,08	±4,29	-335,7	140x90x10	44,4
1-2	1	24	0	0	0	24	25x16x3	2,32
3-4	2	72	12	0	±0,6	84,6	45x28x4.	5,60
5-6	2	24	0	0	о	24	25x16x3	2,32
7-8	2	72	12	0	±0,6	84,6	45x28x4	5,60
9-10	1	24	0	0	0	24	25x16x3	2,32
2-3	2,24	-53,67	0	-13,42	±4,03	-71,12	56x36x5	8,82
3-6	2,83	-33,94	0	-8,49	±3,39	-45,82	45x28x4	5,60
6-7	2,83	-33,94	0	-8,49	±3,39	-45,82	45x28x4	5,60
7-10	2,24	-53,67	0	-13,42	±4,03	-71,12	56x36x5	8,82

сжатых стержней. Условия прочности для растянутого стержня:

(4)

Условие прочности для сжатого стержня:

(5)

Здесь [σ] = 160МПа - допускаемое напряжение для мате­риала стержня; φ - коэффициент продольного изгиба. В столбцах 9 и 10 табл. 1 приведены результаты проектированного расчета элементов фермы в соответствии с сортаментом ГОСТ 8510-72 (сталь прокатная угловая неравнополочная). Для сжатых стерж­ней было принято φ = 0,5, что соответствует гибкости данного элемента λ ≈ 100.