1. Статический расчет плоской рамы

Рамой называется стержневая система с жесткими и шарнирными узлами. Стержни плоской рамы работают на изгиб и растяжение или сжатие. В поперечных сечениях стержней при действии нагрузки возникают, в общем случае, изгибающий момент M, поперечная Q и продольная N силы.

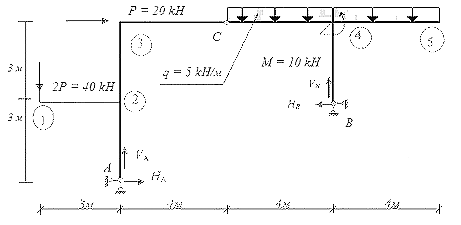Рис. 2

На рис. 2 представлена расчетная схема рамы с указанием размеров, нагрузок, обозначением опорных устройств и реакций, а также сечений, которые являются границами участков опреде­ления М, Q, N (точки приложения сосредоточенных сил, момен­тов, изменения характера действия распределенных нагрузок, пе­реломы оси рамы).

Кинематический анализ выполняется следующим образом. Рама состоит из двух дисков I и II ,соединенных одним простым шарниром С (рисю3).

Т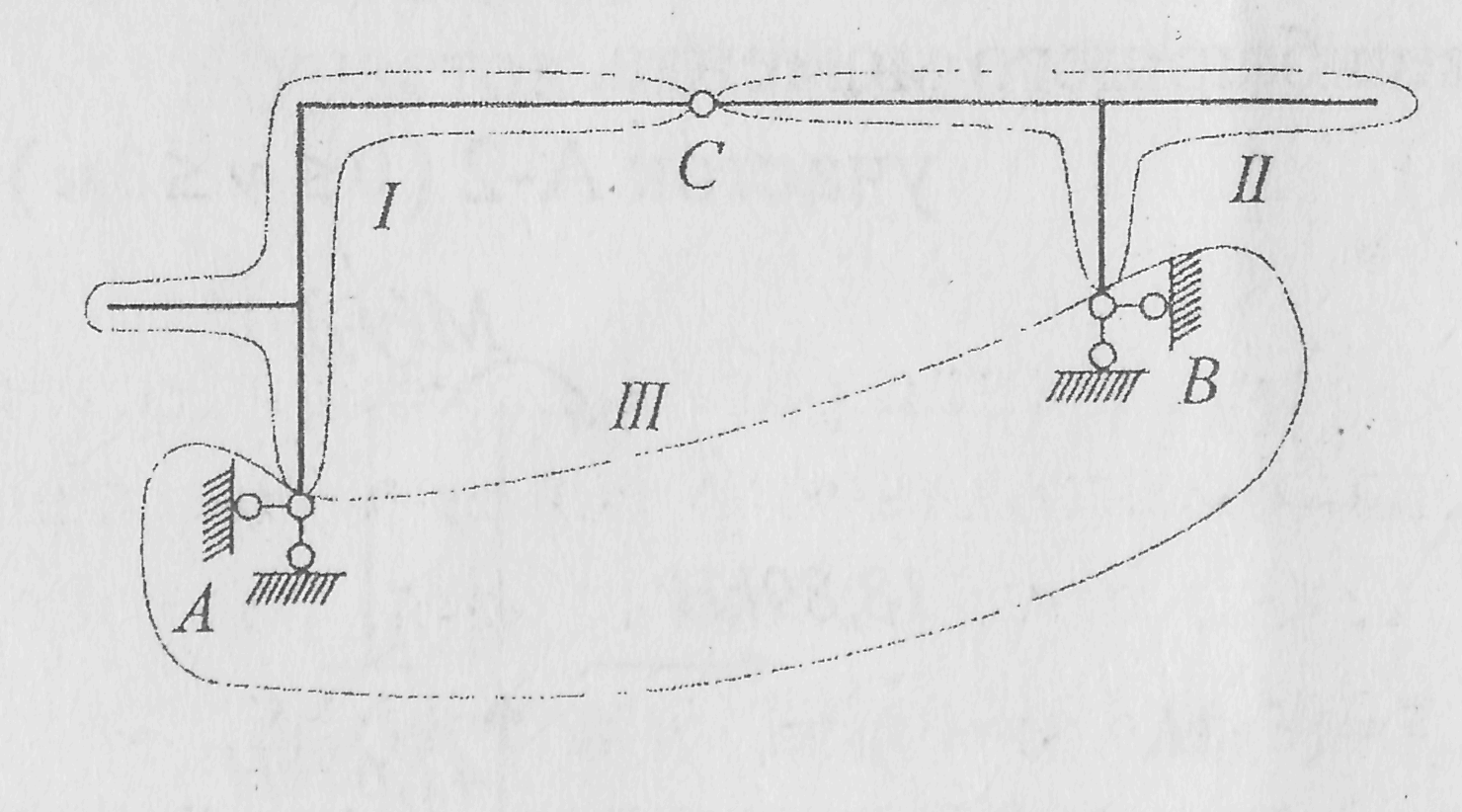аким образом,

D=2, Ш=1

Количество опорных связей

C₀=4(V_A,H_A,V_B,H_B)

W=3x2-2x 1-4=0

Рис.3

Диски I и II, а также диск III (основание) соединены между собой тремя шарнирами А, В, С, не лежащими на одной прямой. Таким образом, данная рама является геометрически неизменяе­мой системой.

Использование метода сечений, в данном случае, предпо­лагает предварительное определение значений опорных реакций. Наиболее рационально они определятся из системы уравнений равновесия:

В результате очевидных преобразований получаем две от­дельно решаемые системы уравнений относительно V_A, H_A и V_B, Н_В:

и ,

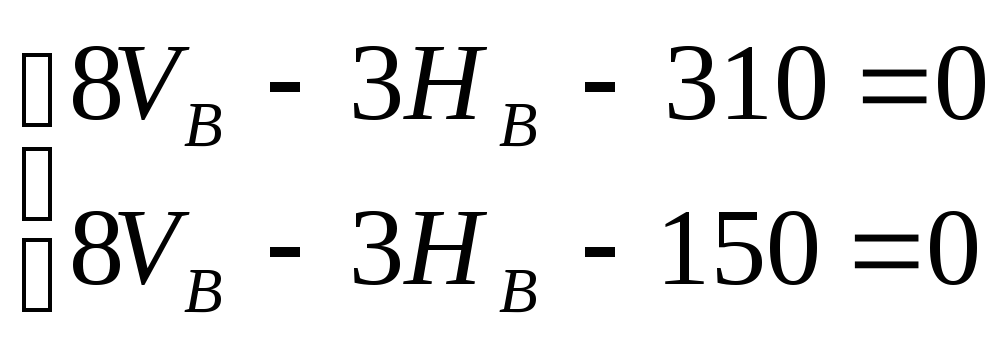решением которых являются значения:

V_A=41,67kH; Н_Л=-18,89 kH; V_B~=38,33kH; H_B=1,11kH.

Знак «-» в значении Н_А указывает, что направление Н_А про­тивоположно, указанному на рис. 2. Учтем это в дальнейшем.

Легко увидеть, что найденные значения удовлетворяют проверкам в смысле равенства нулю проекций всех сил на верти­кальную и горизонтальные оси.

Построим сначала только эпюру М. Для этого рассмотрим последовательно следующие участки:

1-2, А-2, 2-3, 3-С, С-4, 4-5 и 4-В.

Положение растянутого волокна будем определять направ­лением действия искомого изгибающего момента.

участок 1-2 (0 ≤ х ≤ 3м) участок А-2 (0 ≤ у ≤3 м)

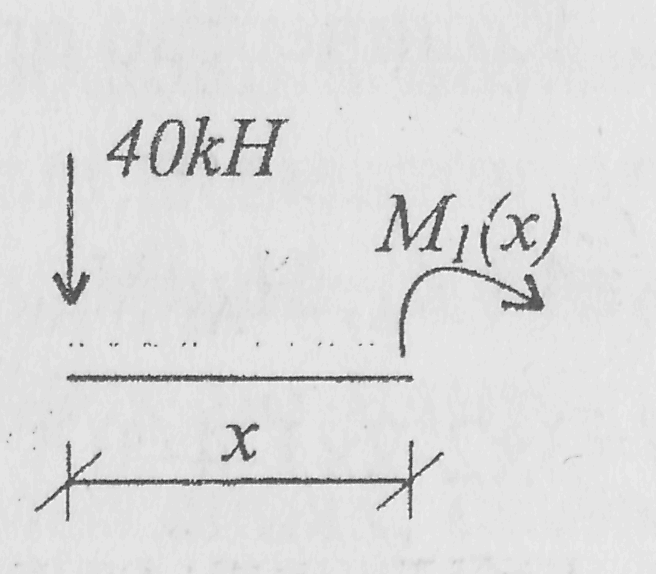
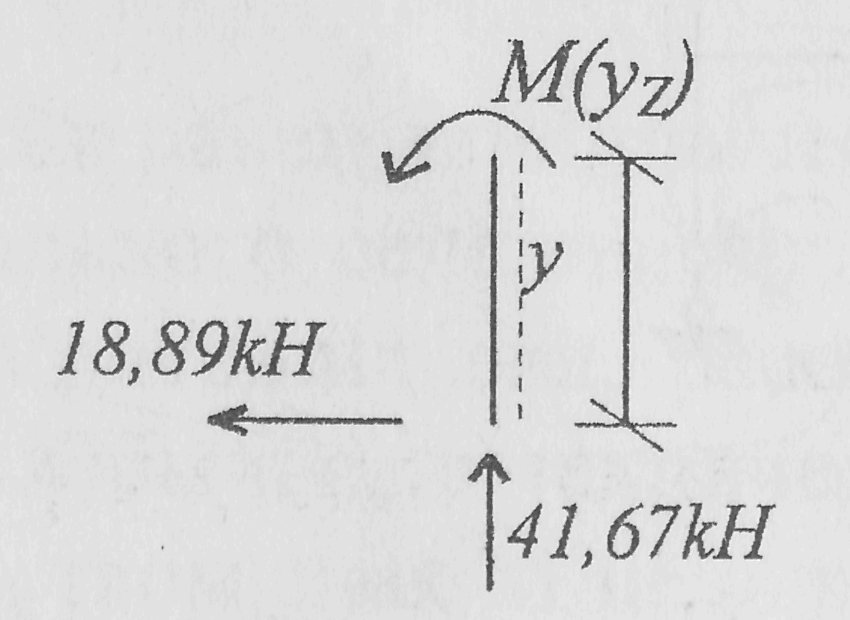
М₁(х) = 40х

М₁(0) = 0

М₁(3) = 120kНм

участок 2-3 (0 ≤ у ≤ 3м)

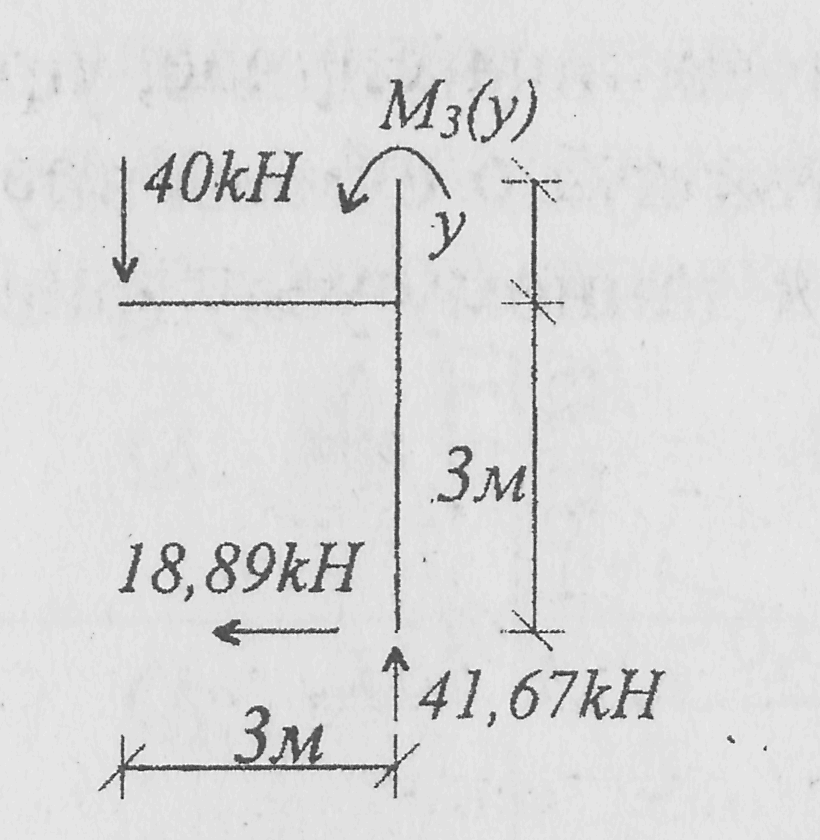
М_z(у) = 18,89у

M_z(0) = 0

М_z(4) = 56,67 kНм

участок 3-С (0 ≤ х ≤ 4м)

Знак «-» определяет растянутое волокно слева .

участок 4-5 (0 ≤ х ≤ 4м) участок С-4 (0 ≤ х ≤ 4м)

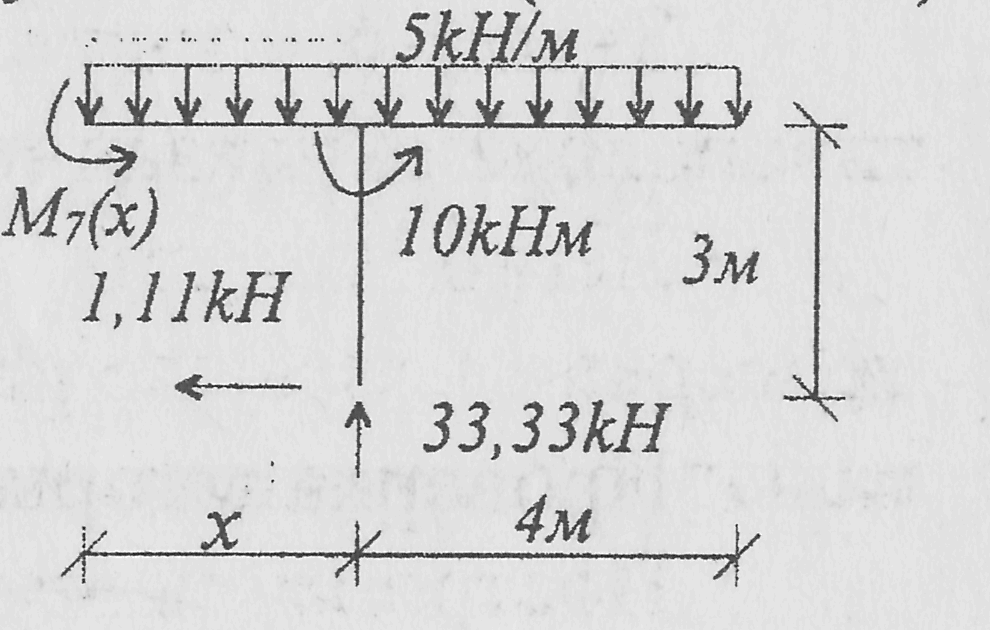
M₇(y) =

М₅(х) = 5х²/2, М₅(0) = 0

М₅(4) = 40kНм

M₇(0) = 33,33

М₇(4) = 0

участок 4-B (0 ≤ у ≤ 3м)

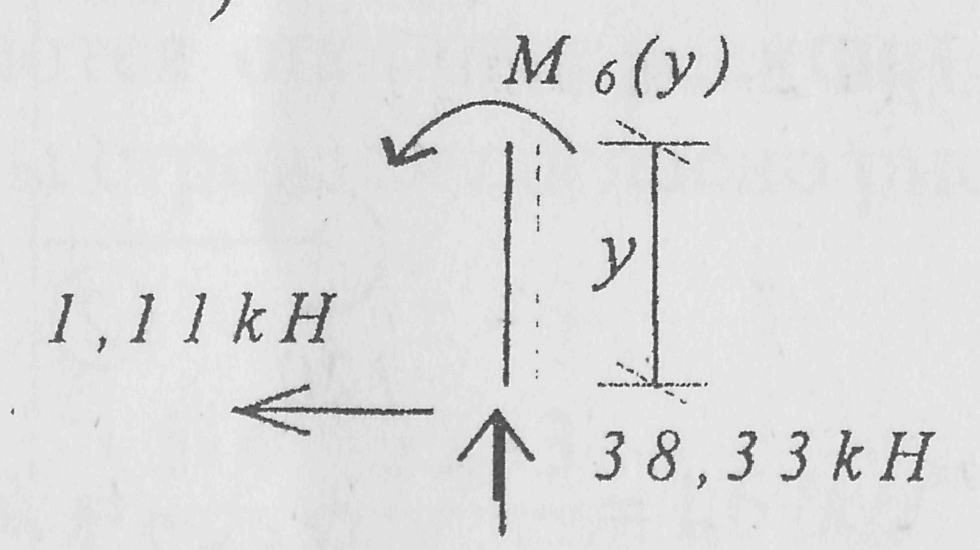
М₆(у) = 1,11у; М₆(0) = 0; М₆(3) = 3,ЗЗkНм

Строим эпюру М в исходной раме, учитывая выражения для М₁, M_z,... M7. Ординаты откладываем со стороны растянутого волокна. Эпюра М представлена на рис. 4.

Для проверки эпюры М используем очевидные условия равновесия узлов рамы в смысле равенства нулю суммы внутрен­них и внешних моментов, приложенных к данному узлу (рис.5).

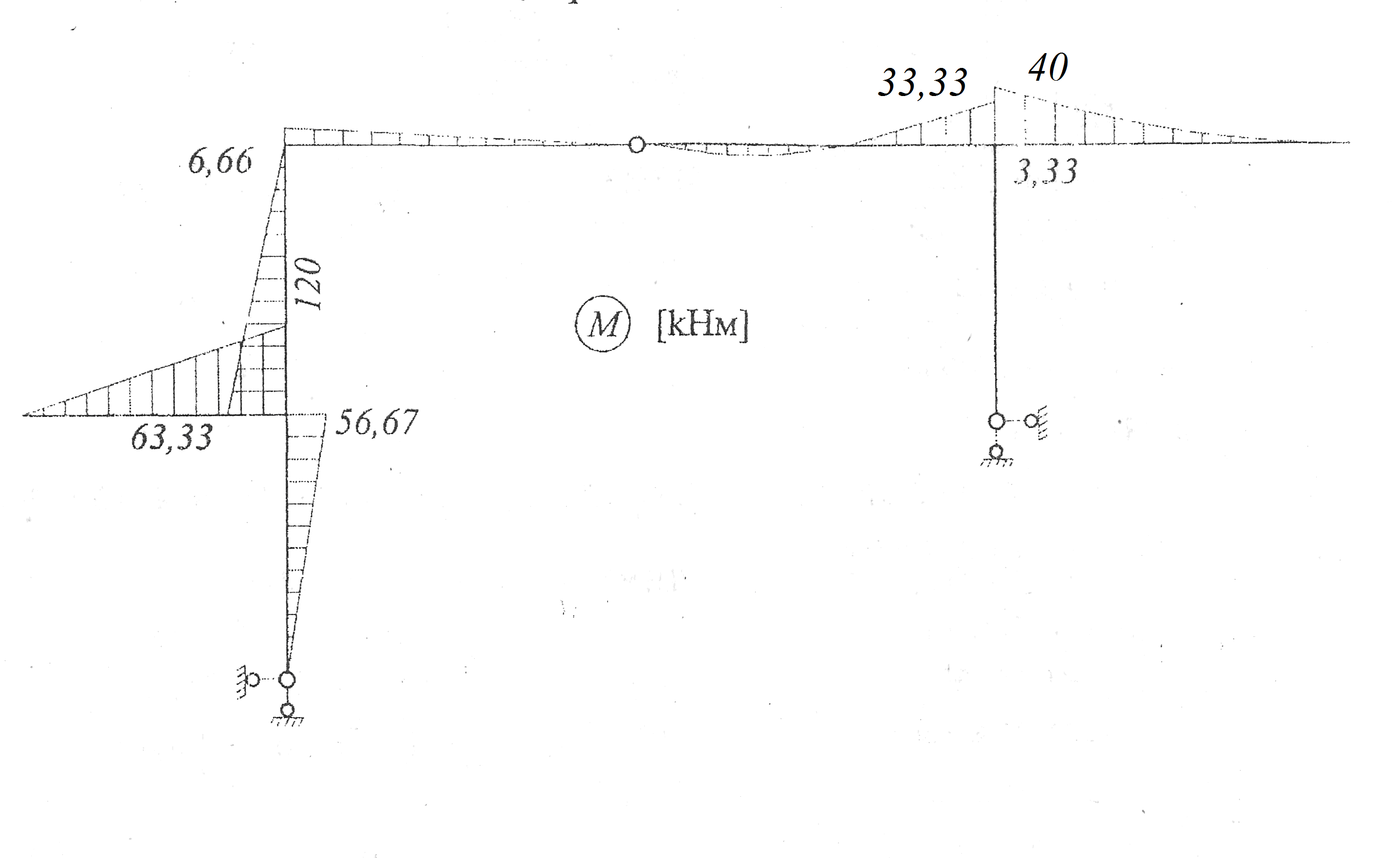
Рис. 4

Проверка эпюры М:

Рис. 5

Эпюру поперечных сил Q удобно строить по эпюре М, ис­пользуя дифференциальную зависимость (теорема Журавского). При этом на линейных участках эпюры М достаточно вычислить тангенсы углов наклона эпюры М к ее оси. Справедливо следующее правило знаков: если ось эпюры М

для совме­щения ее с касательной к эпюре М нужно повернуть на острый угол по часовой стрелке, то Q>o. В этой связи имеем:

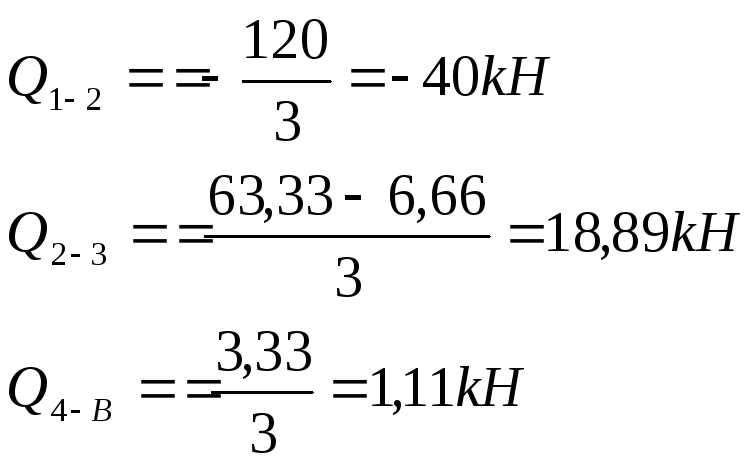
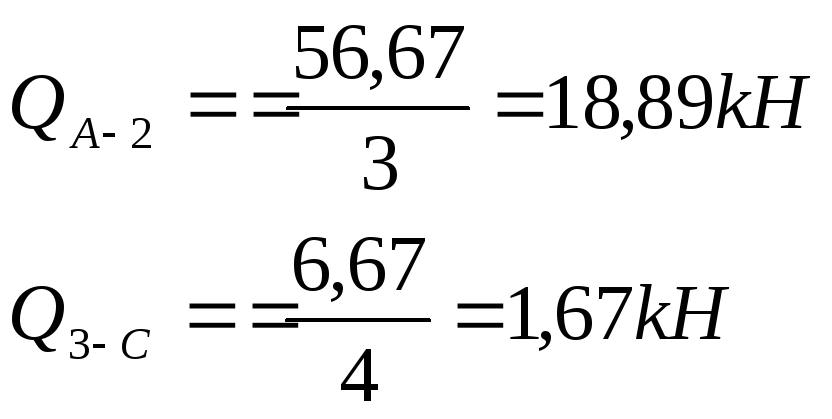
На участке 4-5 поперечную силу рационально можно опре­делить методом сечений:

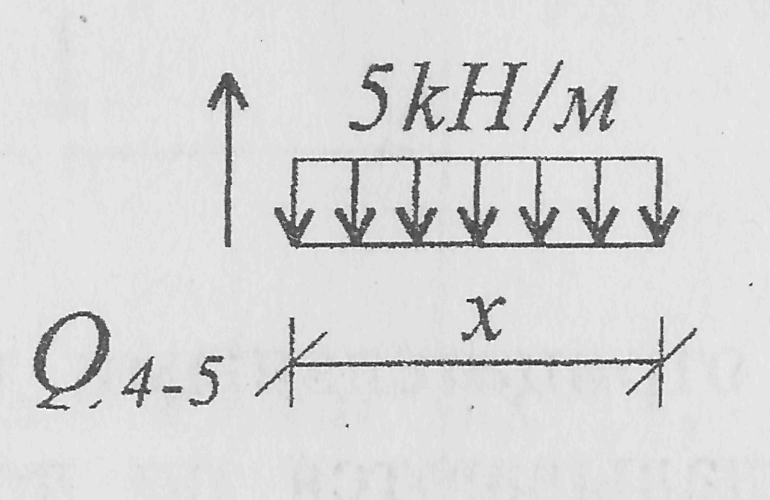
Q_4-5 | _x=0 = 0; Q_4-5 | _x=4м = 20 kH

Эпюра Q для участка с-4 может быть построена следующим образом. Заменим данный участок балкой на шарнирных опорах, нагруженной так, чтобы эпюра изгибающих моментов в ней сов­падала с эпюрой М для рассматриваемого участка рамы.

В балке определим опорные реакции R_} и R₂. Эпюра Q для данного участка рамы строится согласно рис.6.

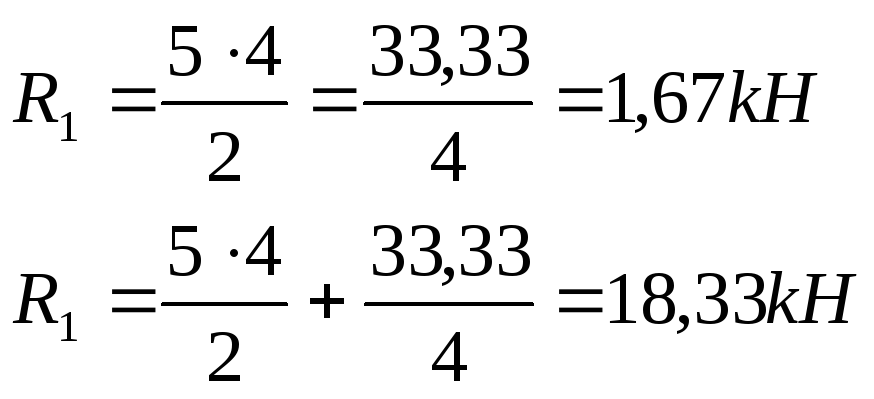
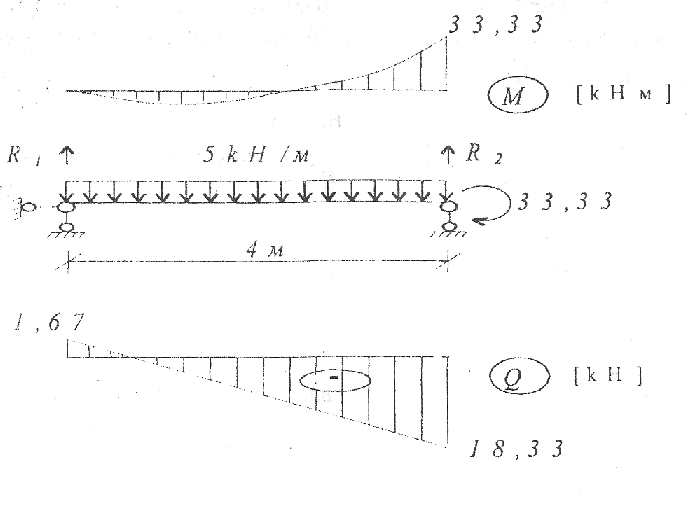
Рис. 6

Если значения Rl и R2 получаются отрицательными, то со­ответствующие ординаты эпюры Q откладываются по другую сторону от ее оси. Эпюра Q для рамы представлена на рис.7.

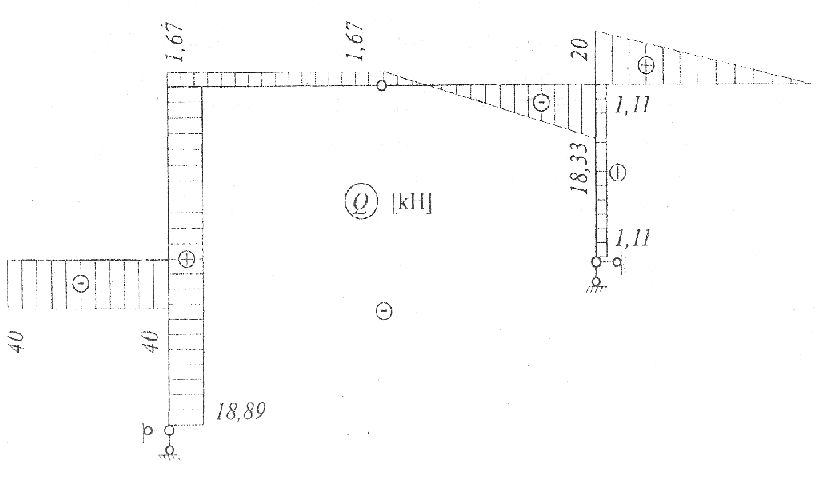
Рис. 7

Эпюра продольных сил N в раме может быть построена со­гласовано с эпюрой q из соображений равновесия узлов рамы в смысле равенства нулю суммы проекций усилий (известных Q и неизвестных n) на оси стержней рамы, образующих данный узел. При этом, начинать рассмотрение условий равновесия следует с узла (узлов), в котором сходятся не более двух стержней.

Эпюра N для рамы представлена на рис.8.

Рис. 8

Условие прочности по нормальным напряжениям для эле­мента рамы имеет следующий вид:

(3)

Здесь: [а]=160 МПа - допускаемое нормальное напряжение для материала рамы (Ст.З); F - площадь сечения определяемого профиля; W_x - момент сопротивления.

Анализ эпюр М и N показывает, что опасным сечением ра­мы является сечение ригеля узла 2, где М=120кНм, N=0. Тогда, из условия прочности имеем:

По таблицам сортамента (ГОСТ 8239-72) определяем дву­тавровый профиль №36, для которого W_x=743 см³, F=61,9 см², Ix=13380cм⁴.