
Математические формулы
Действия над многочленами
![]() –
(a
+ b
– c)x=–ax
– bx
+ cx;
(a
+ b
– c)(x
+ y)=ax
+ ay
+ bx
+ by
– cx
– cy
–
(a
+ b
– c)x=–ax
– bx
+ cx;
(a
+ b
– c)(x
+ y)=ax
+ ay
+ bx
+ by
– cx
– cy
Дроби
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
Формулы сокращённого умножения
![]() 2=
a2
± 2ab + b2
(a ± b)3
= a3
± 3ab2
+ 3a2b
± b3
a2
– b2
= (a–b)(a+b)
2=
a2
± 2ab + b2
(a ± b)3
= a3
± 3ab2
+ 3a2b
± b3
a2
– b2
= (a–b)(a+b)
a3 ± b3 = (a ± b)(a2 ± ab + b2)
Степени
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Корни
![]()
![]()
![]()
![]()
![]()
![]()
![]()
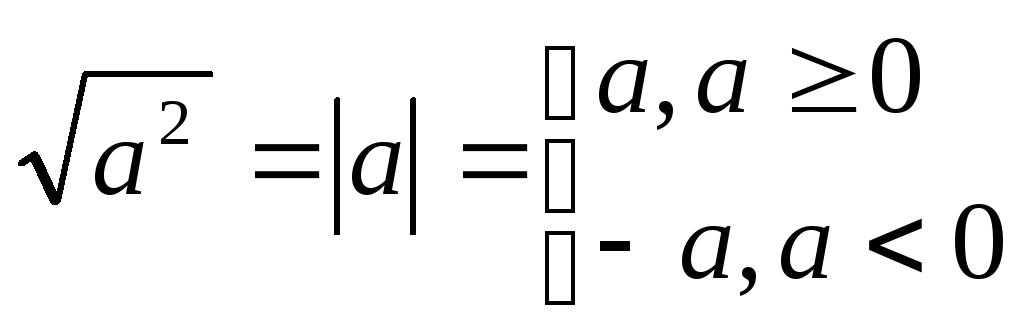
Система двух уравнений первой степени
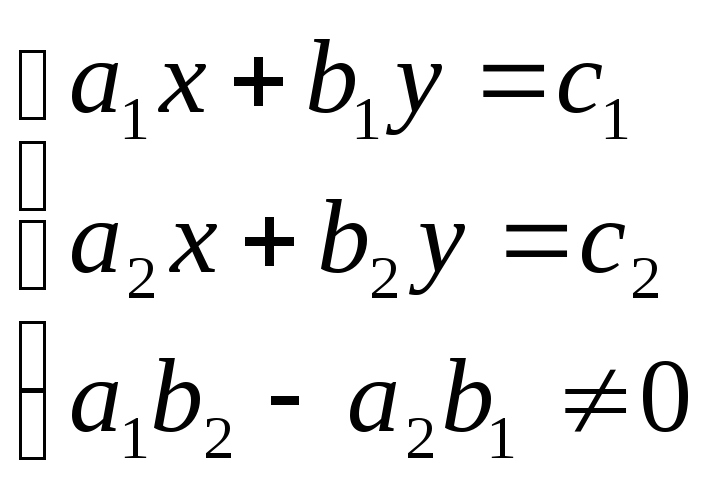
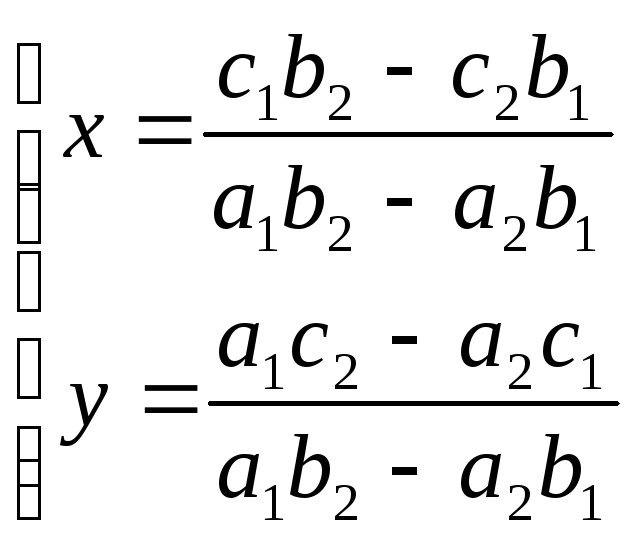
Квадратное уравнение
общего вида: с чётным 2–м коэффициентом
![]()
![]()
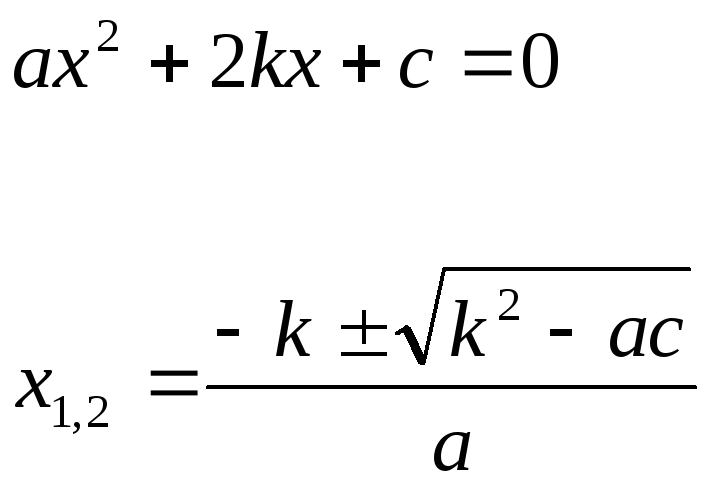
приведённое разложение трёхчлена на множители
![]()
![]()
![]()
теорема Виета для приведённого уравнения
![]()
![]()
Неравенства второй степени
|
D=b2–4ac |
a>0 |
график |
|
|
ax2 + bx + c>0 |
ax2 + bx + c<0 |
||
|
D>0 x1<x2 |
x<x1 x>x2 |
x1<x<x2 |
|
|
D=0 x1=x2 |
x<x1 x>x1 |
нет решений |
|
|
D<0 корней нет |
x
|
нет решений |
|
Неравенства с переменной в знаменателе дроби
1. Неравенство сводиться к системам: 2.Неравенство сводится к системам:
1)
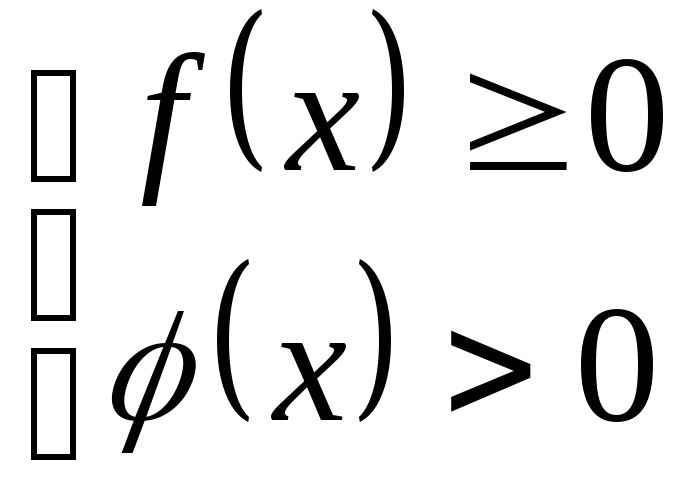 2)
2)
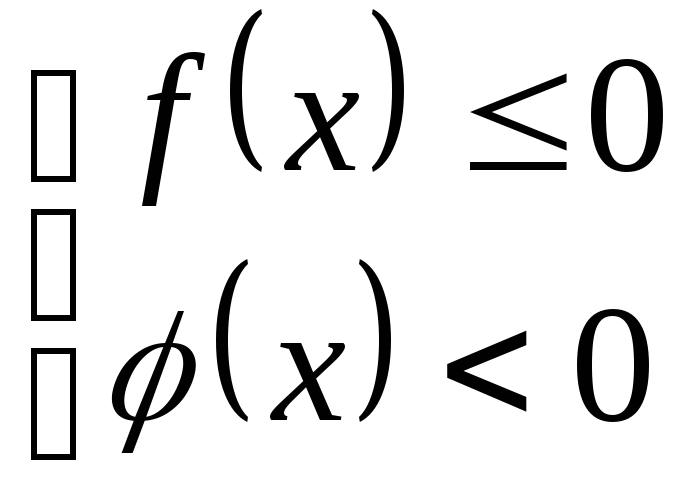 1)
1)
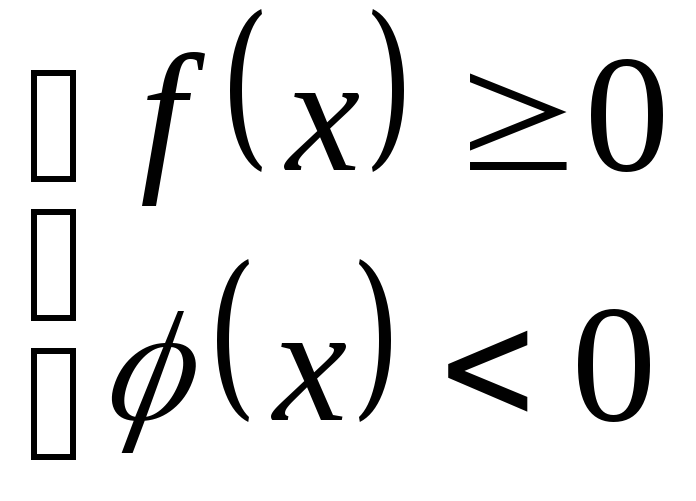 2)
2)
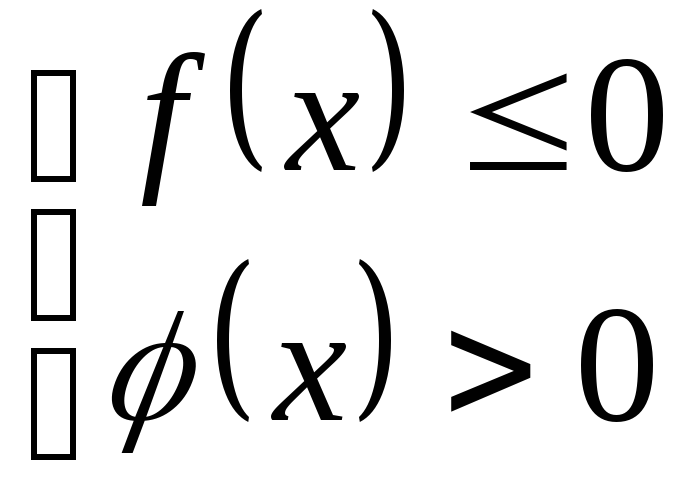
Прогрессии
Арифметическая прогрессия
Общий член
![]() d
– разность прогрессии, т.е.
d
– разность прогрессии, т.е.
![]() или
или
![]()
Сумма n
– первых членов
![]() или
или
![]()
Геометрическая прогрессия
Общий член
![]() где q
– знаменатель прогрессии
сумма членов бесконечно
где q
– знаменатель прогрессии
сумма членов бесконечно
Свойства
геометрической прогрессии:
![]()
![]() убывающей прогрессии:
убывающей прогрессии:
Сумма n
– первых членов
![]() или
или
![]()
![]()
![]()
Логарифмы
Логарифмом числа
b
по основанию a
называется показатель степени c,
в которую нужно возвести основание a,
чтобы получилось число b.
![]()
Основное
логарифмическое тождество:
![]()
![]()
![]()
Свойства логарифмов:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
ЗАМЕЧАНИЕ: все числа a , b , x , y – принимают положительные значения, а если они стоят в основании логарифма, то не равны единице.
Показательные уравнения
1. уравнения вида:
![]() 1) при b<0,
уравнение решения не имеет
1) при b<0,
уравнение решения не имеет
2)
при
![]()
3) при
![]() уравнение можно решить логарифмируя
по основанию а,
уравнение можно решить логарифмируя
по основанию а,
![]()
2. уравнения вида:
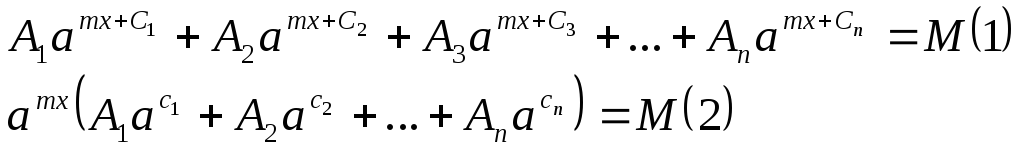 выражение,
находящиеся в скобках уравнения (2),
является величиной постоянной; обозначим
эту величину буквой N,
тогда уравнение (2) примет вид
выражение,
находящиеся в скобках уравнения (2),
является величиной постоянной; обозначим
эту величину буквой N,
тогда уравнение (2) примет вид
![]() ,
при N
≠ 0 имеем:
,
при N
≠ 0 имеем:
![]()
3. уравнение вида:
![]() (1) с помощью подстановки
(1) с помощью подстановки
![]() обращается в обычное квадратное уравнение
обращается в обычное квадратное уравнение
![]() ,
где y1
и y2
– корни. Далее решение уравнения (1)
сводится к решению двух уравнений: 1)
,
где y1
и y2
– корни. Далее решение уравнения (1)
сводится к решению двух уравнений: 1)
![]() 2)
2)
![]()
4. уравнение вида:
![]() легко привести к виду уравнения (1) из
3.
легко привести к виду уравнения (1) из
3.
разделив это
уравнение на
![]() :
:
![]() С помощью подстановки
С помощью подстановки
![]() ,
уравнение принимает вид:
,
уравнение принимает вид:
![]() и сводится к решению двух уравнений: 1)
и сводится к решению двух уравнений: 1)
![]() 2)
2)
![]()
ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА
1.
![]() 1) при
1) при
![]() 2) при
2) при
![]()
аналогично для
неравенства
![]() .
.
2. для неравенства
вида
![]() решение сводиться к решению систем:
решение сводиться к решению систем:
1)
 2)
2)
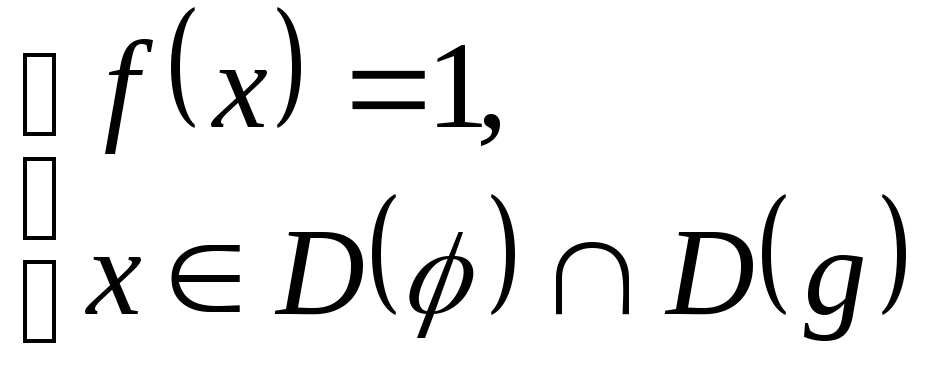 3)
3)
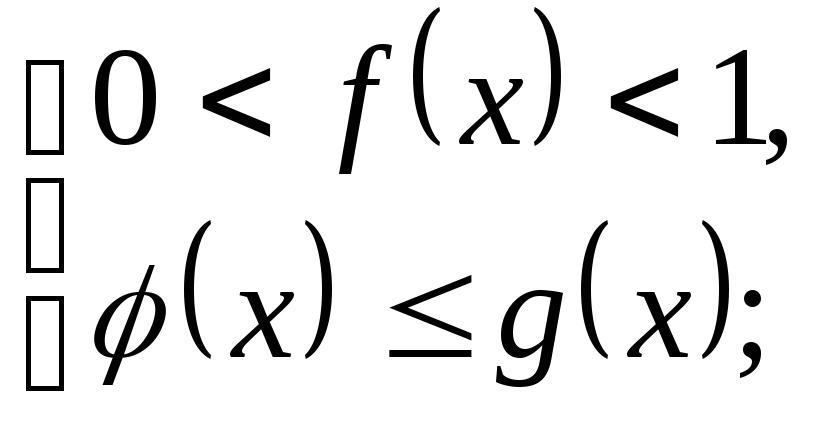 4)
4)
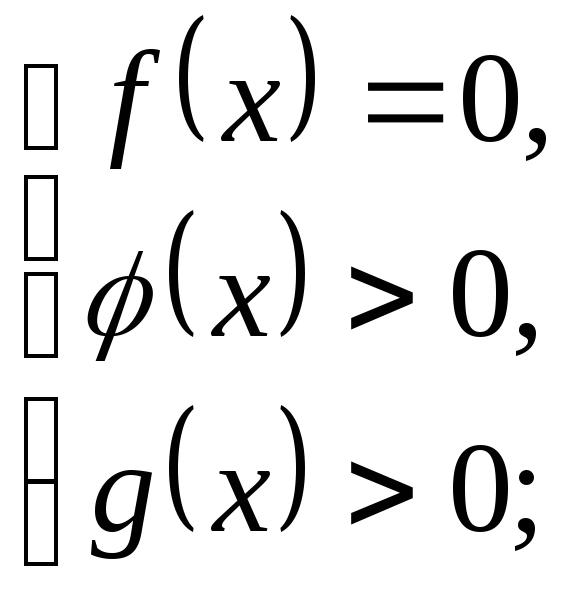
аналогично для
неравенства:
![]()
ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА
1. неравенство вида
![]() сводится к решению одной из систем:
сводится к решению одной из систем:
1) при a>1
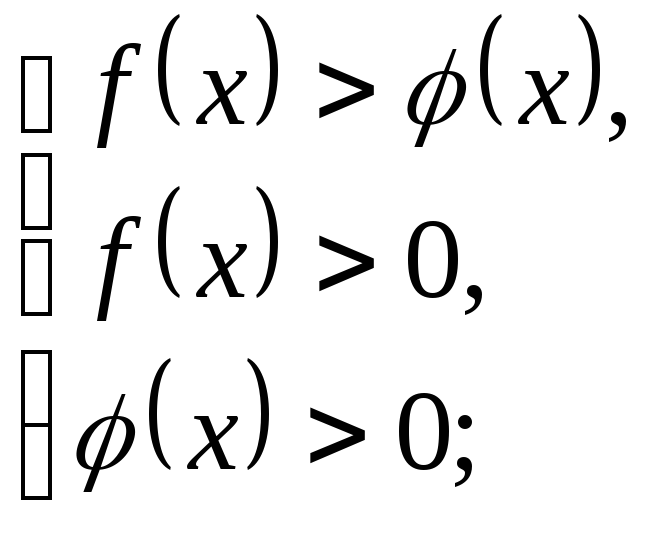 2) при 0<a<1
2) при 0<a<1
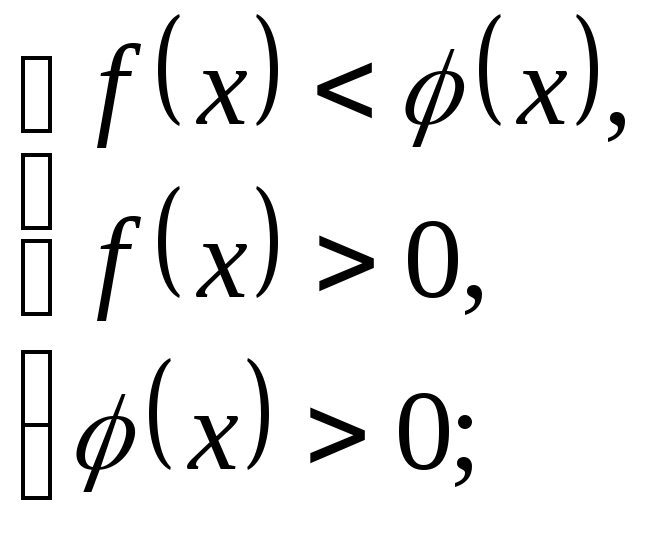 аналогично для неравенства:
аналогично для неравенства:
![]()
2. неравенство вида
![]() сводиться к решению двух систем:
сводиться к решению двух систем:
1)
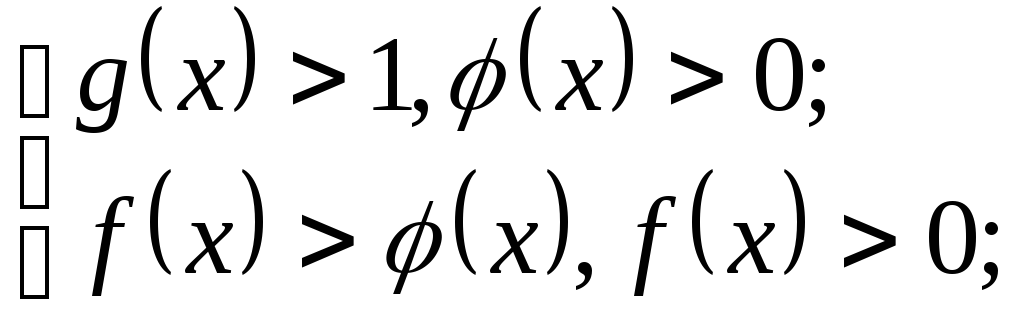 2)
2)
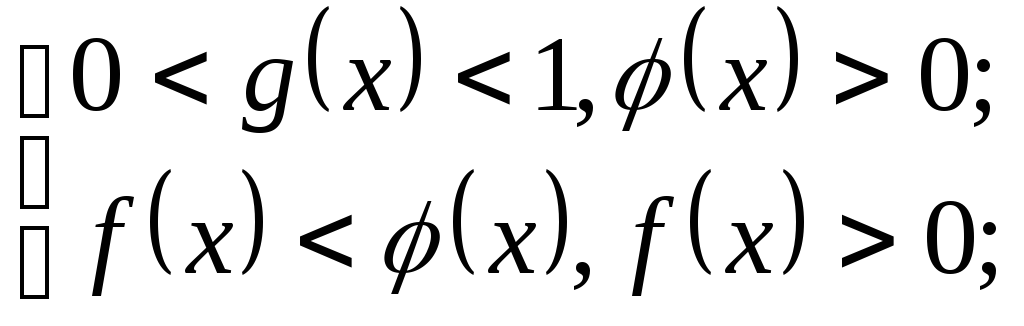 аналогично для неравенства
аналогично для неравенства
![]()
ПРОИЗВОДНАЯ
![]() значение
производной функции в точке
значение
производной функции в точке
![]() равно угловому коэффициенту касательной
к графику функции в этой точке.
равно угловому коэффициенту касательной
к графику функции в этой точке.
![]() – уравнение касательной к графику
функции
– уравнение касательной к графику
функции
![]() в точке
в точке
![]()
ФОРМУЛЫ ПРОИЗВОДНЫХ ОСНОВНЫХ ФУНКЦИЙ
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
![]()
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Определение
![]() Радианная мера углов 1радиан
= 1800/π
≈57,295779520;
Радианная мера углов 1радиан
= 1800/π
≈57,295779520;
10 = π/1800 радиан ≈ 0,001745 рад.
Знаки тригонометрических функций
|
|
sin α |
cos α |
tg α |
ctg α |
|
0< α <π/2 |
+ |
+ |
+ |
+ |
|
π/2< α < π |
+ |
– |
– |
– |
|
π< α <3π/2 |
– |
– |
+ |
+ |
|
3π/2< α <2π |
– |
+ |
– |
– |
Значения функций характерных углов
|
радианы |
0 |
π/6 |
π/4 |
π/3 |
π/2 |
π |
3π/2 |
2π |
|
градусы |
00 |
300 |
450 |
600 |
900 |
1800 |
2700 |
3600 |
|
sin α |
0 |
½ |
√2/2 |
√3/2 |
1 |
0 |
–1 |
0 |
|
cos α |
1 |
√3/2 |
√2/2 |
½ |
0 |
–1 |
0 |
1 |
|
tg α |
0 |
√3/3 |
1 |
√3 |
∞ |
0 |
∞ |
0 |
|
ctg α |
∞ |
√3 |
1 |
√3/3 |
0 |
∞ |
0 |
∞ |
Формулы приведения. Чётность.
|
аргумент |
функция |
sin |
cos |
tg |
ctg |
|
–α |
–sinα |
cosα |
–tgα |
–ctgα |
|
|
π/2 ± α |
cosα |
|
|
|
|
|
π ± α |
|
–cosα |
|
|
|
Основные соотношения
sin2α + cos2α = 1; tgα · ctgα = 1; tgα = sinα/cosα = 1/ctgα; ctgα = cosα/sinα = 1/tgα;
1 + tg2α = 1/cos2α; 1 + ctg2α = 1/sin2α; secα = 1/cosα; cosecα = 1/sinα;
Периодичность
функции sinα и cosα имеют период 2π, а функции tgα и ctgα – период π.
sin(α
+ 2πn)
= sinα,
n![]() Z;
cos(α
+ 2πn)
= cosα,
n
Z;
cos(α
+ 2πn)
= cosα,
n![]() Z;
tg(α
+ πn)
= tgα,
n
Z;
tg(α
+ πn)
= tgα,
n![]() Z;
ctg(α
+ πn)
= ctgα,
n
Z;
ctg(α
+ πn)
= ctgα,
n![]() Z;
Z;
Формулы для суммы и разности аргументов.
sin(α
± β)
= sinα
· cosβ
± cosα
· sinβ;
cos(α
± β)
= cosα
· cosβ
![]() sinα
· sinβ;
sinα
· sinβ;
tg(α
± β)
= (tgα
± tgβ)
/ (1
![]() tgα
· tgβ);
ctg(α
± β)
= (ctgα
· ctgβ
tgα
· tgβ);
ctg(α
± β)
= (ctgα
· ctgβ
![]() 1) / (ctgβ
± ctgα);
1) / (ctgβ
± ctgα);
Функции двойных углов
sin2α = 2sinα · cosα; cos2α = cos2α – sin2α = 1–2sin2α = 2cos2α – 1; tg2α = 2tgα / (1–tg2α);
ctg2α = (ctg2α – 1) / 2ctgα;
Функции половинного угла
sin(α/2) =
±
![]() cos(α/2) = ±
cos(α/2) = ±
![]() tg(α/2) = ±
tg(α/2) = ±![]()
2sin2(α/2) = 1 – cosα; 2cos2(α/2) = 1 + cosα; sin2α = (1–cos2α) / 2
Функции полного угла
sinα = 2tg(α/2) / (1+ tg2(α/2)); cosα = (1–tg2(α/2)) / (1+tg2(α/2)); tgα = 2tg(α/2) / (1–tg2(α/2));
Функции тройного угла
sin3α = 3sinα – 4sin3α; cos3α = 4cos3α – 3cosα;
Произведения тригонометрических функций
sinα · cosβ = ½ · (sin(α + β) + sin(α – β)); cosα · cosβ = ½ · (cos(α + β) + cos(α – β));
sinα · sinβ = ½ · cos(α – β) – cos(α + β));
Сумма и разность тригонометрических функций
sinα + sinβ = 2 · sin((α + β)/2) · cos((α – β)/2); sinα – sinβ = 2 · sin((α – β)/2) · cos((α + β)/2);
cosα + cosβ = 2 · cos((α + β)/2) · cos((α – β)/2); cosα – cosβ = 2 · sin((α + β)/2) · sin((α – β)/2);
tgα ± tgβ
= sin(α ± β) / (cosα · cosβ); cosα ± sinα =
![]() ;
;
Тригонометрические уравнения
sinα = a,
α = (–1)n
· arcsin a + π·n, n![]() Z;
cosα = a, α = ± arccos a + 2π, n
Z;
cosα = a, α = ± arccos a + 2π, n![]() Z;
Z;
tgα = a,
α = arctg a + π·n, n![]() Z;
ctgα = a, α = arcctg a + π·n, n
Z;
ctgα = a, α = arcctg a + π·n, n![]() Z;
Z;
Частные случаи
sin x = ±1,
x = ± π/2 + 2π, n![]() Z;
sin x = 0, x = πn, n
Z;
sin x = 0, x = πn, n![]() Z;
cos x = –1, x = π + 2πn, n
Z;
cos x = –1, x = π + 2πn, n![]() Z;
Z;
cos x = 0,
x = π/2 + πn, n![]() Z;
cos x = 1, x = 2πn, n
Z;
cos x = 1, x = 2πn, n![]() Z;
Z;
Обратные тригонометрические функции отрицательного аргумента
arcsin(–α) = –arcsinα; arccos(–α) = π – arccosα; arctg(–α) = –arctgα; arcctg(–α) = –arcctgα;
ГЕОМЕТРИЯ
МЕТОД КООРДИНАТ
Пусть на (i,
j,
k)
заданы
![]() ,
тогда операции над ними будут равны:
,
тогда операции над ними будут равны:
![]()
![]() ;
;
![]()
![]()
![]()
![]()
![]() Пусть A
( x1;
y1;
z1);
B
(x2;
y2;
z2);
тогда:
Пусть A
( x1;
y1;
z1);
B
(x2;
y2;
z2);
тогда:
вектор![]() ;
модуль вектора
;
модуль вектора![]()
ТРЕУГОЛЬНИК
в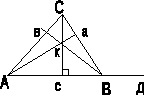 нешний
угол СВД
=
нешний
угол СВД
=
![]() ;
К – точка пересечения высот (ортоцентр
треугольника). ha,
hb,
hc
– высоты треугольника на соответствующие
стороны.
;
К – точка пересечения высот (ортоцентр
треугольника). ha,
hb,
hc
– высоты треугольника на соответствующие
стороны.
![]()
![]() где полупериметр
где полупериметр
![]()
![]() .
.
![]()
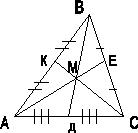 М
– точка пересечения медиан треугольника
(центр тяжести).
М
– точка пересечения медиан треугольника
(центр тяжести).
ma, mb, mc – медианы на соответствующие стороны. МВ:МД=МА:МЕ=МС:МК=2/1
![]()
![]()
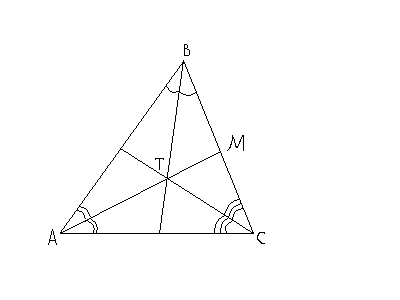
![]() Т
– точка пересечения биссектрис
треугольника (центр вписанной окружности).
La,
Lb,
Lc
– биссектрисы соответствующих углов.
ВМ:МС = АВ:АС
Т
– точка пересечения биссектрис
треугольника (центр вписанной окружности).
La,
Lb,
Lc
– биссектрисы соответствующих углов.
ВМ:МС = АВ:АС
![]()
![]()
r
– радиус вписанной окружности. О –
точка пересечения серединных
перпендикуляров к сторонам треугольника
(центр описанной окружности). Радиус
описанной окружности:
![]()

![]()
![]() где
SΔ
– площадь треугольника; p
– периметр треугольника; hc
–
где
SΔ
– площадь треугольника; p
– периметр треугольника; hc
–
высота опущенная на соответствующую сторону с. На всех 4–х нарисованных треугольниках стороны одинаково обозначены, просто на 1–м они обозначены, а на остальных они опущены для упрощения рисунка. И вообще подразумевается, что все 4 треугольника абсолютно одинаковые.
M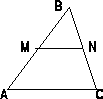 N
– средняя линяя треугольника. MN=0.5AC;
MN║AC.
N
– средняя линяя треугольника. MN=0.5AC;
MN║AC.
ТЕОРЕМА СИНУСОВ
![]()
![]() где R
– радиус описанной окружности.
где R
– радиус описанной окружности.
![]()
![]()
![]() ТЕОРЕМА
КОСИНУСОВ
ТЕОРЕМА
КОСИНУСОВ
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ПЛОЩАДЬ ТРЕУГОЛЬНИКА
![]()
![]() где
где
![]() –
длины сторон
треугольника, а
–
длины сторон
треугольника, а
![]() –
высоты, опущенные
на соответствующие стороны.
–
высоты, опущенные
на соответствующие стороны.
![]()
![]()
![]()
![]() – формула Герона.
– формула Герона.
РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК
![]() тогда площадь
тогда площадь
![]()
ПРАВИЛЬНЫЙ ТРЕУГОЛЬНИК
![]()
![]()
![]()
![]()
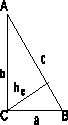
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
а и b – катеты, с – гипотенуза, ас и bc – проекции катетов на гипотенузу.
а2 + b2 = c2 – теорема Пифагора.
S=
a·b/2
= c·hc/2;
![]()
![]() – радиус вписанной окружности.
– радиус вписанной окружности.
![]() R
= c/2,
– радиус описанной окружности.
R
= c/2,
– радиус описанной окружности.
![]()
![]() sinA
= a/c; cosA = b/c; tgA = a/b; ctgA = b/a; b2
= c·bc;
sinA
= a/c; cosA = b/c; tgA = a/b; ctgA = b/a; b2
= c·bc;
![]() a
= c·sinA = c·cosB = b·tgA = b·ctgB; c = a/sinA = a/cosB = 2R;
a
= c·sinA = c·cosB = b·tgA = b·ctgB; c = a/sinA = a/cosB = 2R;
![]()
ПАРАЛЛЕЛОГРАММ
![]()
![]()
![]()
![]()
![]()
П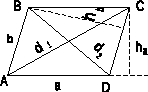 РЯМОУГОЛЬНИК
РЯМОУГОЛЬНИК
![]()
РОМБ
![]()
![]()
КВАДРАТ
![]()
![]()
![]()

ТРАПЕЦИЯ
![]() а
и b
–
основания, h
– высота
а
и b
–
основания, h
– высота
![]()
ОКРУЖНОСТЬ И КРУГ
Длина окружности с =2πR. Площадь круга S = πR2 = πD2/4.
Длина дуги l = π·R·α/1800. Площадь сектора S = π·R2·α/3600.
где α – величина угла дуги в градусах.
ЧЕТЫРЁХУГОЛЬНИК И КРУГ
Свойство вписанного
четырёхугольника:
![]()
ac + bd = ef, где a,b,c,d – стороны, e,f – диагонали.
Свойство описанного четырехугольника: a + c = b + d;
S = p·r, p – полупериметр.
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ
Внутренний угол
![]() где
n
– число сторон. an
= 2R·sin(1800/n);
где
n
– число сторон. an
= 2R·sin(1800/n);
Sn = ½ ·n·an·r; Sn = ½ ·Pn·r; r = R·cos(1800/n);
ШЕСТИУГОЛЬНИК
![]()
СТЕРЕОМЕТРИЯ
ПРИЗМА
Боковая поверхность наклонной призмы Sб.п. = P1·l, где P1 – периметр перпендикулярного сечения, l – ребро призмы. Боковая поверхность прямой призмы Sб.п. = Pосн ·l; Объём призмы Vпр=Sосн·h;
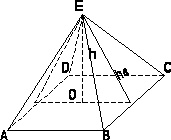
ПИРАМИДА
I

 .
Если боковые рёбра
пирамиды равнонаклонены к плоскости
основания (их длины равны), то высота
проходит через центр окружности описанной
около многоугольника основания.
.
Если боковые рёбра
пирамиды равнонаклонены к плоскости
основания (их длины равны), то высота
проходит через центр окружности описанной
около многоугольника основания.
II. Если боковые грани пирамиды равнонаклонены к плоскости основания (длины апофемы равны), то высота проходит через центр окружности, вписанной в многоугольник основания.
Площадь боковой поверхности правильной пирамиды: Sб.пир.= ½ ·Pосн·ha , где ha – апофема.
Sб.пир.= Sосн /cosα , где α – угол наклона боковой грани к основанию.
Объём пирамиды: Vпир= ⅓·Sосн·h, где h – высота пирамиды.
Площадь боковой поверхности правильной усечённой пирамиды: Sбок= ½ ·(P1+P2)·ha , где P1, P2 – периметры оснований (верхнего и нижнего); ha – апофема.
Объём усечённой
пирамиды:
![]() где
Q1
и Q2
– площади оснований.
где
Q1
и Q2
– площади оснований.
ТЕЛА ВРАЩЕНИЯ
ЦИЛИНДР
Площадь боковой поверхности: Sбок =2·π·R·h; Площадь всей пов–ти: S=2·π·R·(R + h); Объём: V = πR2·h;
КОНУС
Площадь пов–ти конуса: боковой Sб=πrl; полной Sп=πr ·(r + l); где l – образующая. Объём: V=πr2h/3;
УСЕЧЁННЫЙ КОНУС
Площадь боковой пов–ти: Sб.у.к.= π·l·(R + r); Объём: V=⅓·π·h(R2 + r2 +Rr); угол развёртки: α=(R–r)/l;
ШАР
Площадь пов–ти сферы: Sсф=4πR2; Объём шара: Vш=4/3·πR 3;
ТАБЛИЦА ПЕРВООБРАЗНЫХ ИНТЕГРАЛОВ
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)
![]()
7)
![]()
8)
![]()
9)
![]()
10)
![]()
11)
![]()
12)
![]()
13)
![]()
14)
![]()
15)
![]()
16)
![]()
17)
![]()
18)
![]()
19)
![]()
20)
![]()
21)
![]()
22)
![]()
