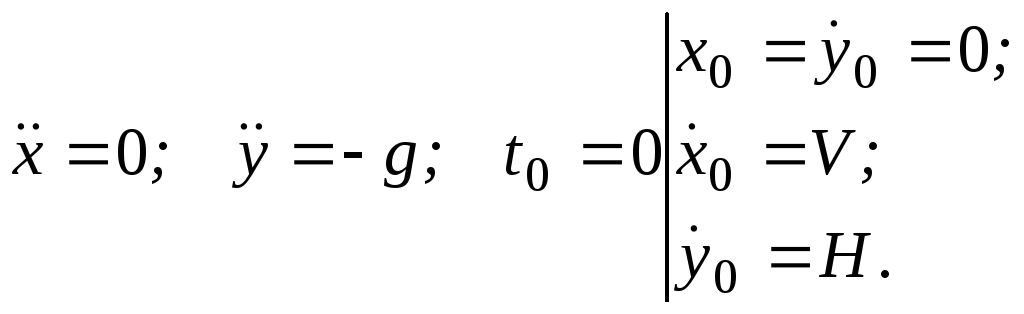1.3.29 Точка м масою m вилітає з початковою швидкістю Vо під кутом  до горизонту з точки о. Вкажіть диференціальне рівняння руху точки і відповідні початкові умови.

а)
б)
в)
г)
д)

1.3.30 Точка м, маса якої m, випущена з висоти н під кутом  до горизонту з початковою швидкістю Vо . Запишіть диференціальне рівняння руху точки і відповідні початкові умови.

а)
б)
в)
г)
д)

1.3.31 Снаряд М масою m вилітає з точки О зі швидкістю V_о під кутом  до горизонту. Запишіть диференціальне рівняння руху снаряда і відповідні початкові умови, якщо сила опору повітря R = -kmV².

а)
б)
в)
г)
д)

1.3.32 Камінь м вагою р кинули згори висотою н пара-лельно осі Ох зі швидкістю Vо . Запишіть диференціальне рівняння руху каменя і початкові умови його руху.

а)
б)
в)
г)
д)

1.3.33 Тіло М масою m падає з деякої висоти Н без початкової швидкості, долаючи опір середовища, сила якого R = kV². Запишіть диференціальне рівняння і початкові умови руху тіла, якщо вісь Оу направлена вниз з початкового положення.

а)
б)
в)
г)
д)

1.3.34 Точка М, маса якої m, падає під дією сил тяжіння з висоти Н без початкової швидкості V_о. Запишіть диференціальне рівняння і початкові умови руху точки.

а) б) ; в) г) д)

1.3.35 Тіло М масою m ковзає по шорсткій похилій площині, з кутом  до горизонту під дією сили тяжіння Р. Коефіцієнт тертя ковзання тіла до площини дорівнює f. Запишіть диференціальне рівняння і початкові умови руху тіла, якщо в початковий момент часу воно перебувало в стані спокою.

а)
б)
в)
г)
д)

1.3.36 Матеріальна точка М вагою Р рухається із стану спокою вздовж горизонтальної осі Ох під дією сили , де k – додатна стала. Запишіть диференціальне рівняння і початкові умови руху тіла.

а); б) ; в) ; г) ; д)

1.3.37 Літак летить горизонтально на висоті Н зі швидкістю V. Запишіть диференціальні рівняння руху вантажа вагою Р, скинутого з цього літака без відносної початкової швидкості, і відповідні початкові умови, обравши початок координат у точці відокремлення вантажа від літака.

а) б) в) г) д)

1.3.38 Тіло М масою m = 2 кг кинуто вертикально вгору зі швидкістю V_о = 20 м/с. Сила опору руху тіла пропорційна швидкості і дорівнює R = 0,04V (Н). Визначте час, за який тіло досягне найвищого положення.

а) t  2 с; б) t  4 с; в) t  1,5 с; г) t  1 с; д) t  3 с.

1.3.39 Снаряд вагою Р масою m вилітає зі швидкістю V_о під кутом  до горизонту. Сила опору повітря R = kV. Запишіть диференціальне рівняння і початкові умови руху снаряда.

а)
б)
в)
г)
д)

1.3.40 Матеріальна точка М масою m = 1 кг рухається вздовж горизонтальної осі Ох під дією сили (Н). Вважаючи початкові умови руху точки нульовими, знайдіть координату х₁, точки в момент часу t₁ = 1 с.

а) х1 = (l + е) м; б) х1 = е2 м; в) х1 = lnе м; г) х1 = (е – 2) м; д) м.