Задание с2
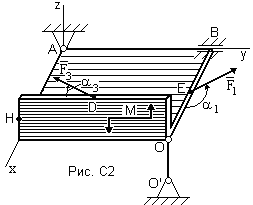
Две однородные
прямоугольные плиты, сваренные под
прямым углом друг к другу, закреплены
с помощью связей в точках А,
В, О. Размеры
плит в направлениях, параллельных
координатным осям х,
у, z
равны соответственно или
,
и
.
В меньшей из плит сделан вырез в виде в
виде прямоугольного равнобедренного
треугольника с гипотенузой равной
.
Середина гипотенузы, которая совпадает
со стороной плиты, находится в точке H.
Вес большей плиты равен G1
= 5 кН,
вес меньшей плиты (без выреза) -
2 КН. Каждая из плит расположена параллельно одной из координатных плоскостей (плоскость ху горизонтальная).
На плиты
действуют пара сил с моментом М
= 5 кНм,
и две силы
и
при этом сила
лежит в плоскости
хАу, сила
лежит в плоскости, параллельной плоскости
уАz.
Точки приложения сил находятся в
серединах сторон плит.
Найти
координаты центра тяжести конструкции
и определить реакции связей в точках
А, В, О.
При расчетах принять
= 0,5
м,
F1=
20
кН,
α1
= 1350,
F3
= 30 кН,
α3
= 300.
Толщиной плит пренебречь.
Решение
Определим координаты центра тяжести конструкции, для этого изобразим на малой плите вырез.
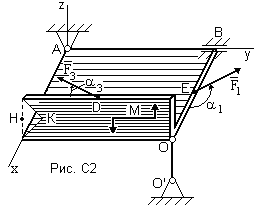
Центр тяжести большей плиты находится на пересечении диагоналей, его координаты равны
=
,
=
,
.
Для определения центра тяжести меньшей плиты воспользуемся методом отрицательных площадей, в этом случае вырез в виде треугольника будем считать отрицательной массой. Центр тяжести меньшей плиты без выреза находится на пересечении диагоналей, его координаты равны
=
,
=
,
.
Центр тяжести выреза в виде треугольника находится на пересечении медиан, его координаты равны
=
,
=
,
.
Используя формулы координат центра тяжести тела по методу отрицательных площадей, найдем требуемые координаты центра тяжести всей конструкции
,
=
,
,
где S1, S2, S3 – площади соответственно большей и меньшей плит, и выреза в виде треугольника.
Подставляя в
формулы заданное значение
= 0,5 м, получим
координаты центра тяжести всей конструкции
=
0,657 м,
=
0,769 м,
=
0,0785 м.
Для нахождения реакций связей покажем, кроме заданных сил и момента сил M, силу тяжести конструкции G (координаты точки приложения силы мы только что нашли) и реакции связей в точках А, В, О.
Величина силы
тяжести конструкции равна
,
где G3
– сила тяжести вырезанного треугольника
G3
=
=
=
0,167 кН,
тогда
G = 5 + 2 – 0,167 = 6,83 кН.
Для полученной на
рисунке произвольной пространственной
системы сил запишем условия и составим
уравнения равновесия конструкции. При
составлении уравнений моментов сил
используем теорему Вариньона, для чего
силы
и
разложим на составляющие
и
,
где
,
.
∑Fix
= 0 XА
+ ХВ
+ F1cos
= 0;
(1)
∑Fiy
= 0 YA
+ F1sin
–F3cos
= 0; (2)
∑Fiz
= 0
;
(3)
∑Mхi
= 0
;
(4)
∑Mуi
= 0
;
(5)
∑Mzi
= 0
.
(6)
Из уравнения (6)
найдем
(-
,
из уравнения (5)
найдем
,
из уравнения (4)
найдем
.
Зная реакции
,
,
не представляет труда из уравнений (1),
(2), (3) найти выражения для остальных
неизвестных реакций
XА
= - ХВ
- F1cos
,
YA
= - F1sin
+ F3cos
,
.
Произведем вычисления реакций
(-
= 0,76 кН,
= 3,01 кН,
= 3,18 кН,
XА = - 0,76 + 10·cos1350 = – 7,83 кН,
YA = - 10sin 1350 + 15 cos 300 = 5,92 кН,
= –
0,84
кН.