2.1.2. Законы Ома и Джоуля-Ленца Обобщенный закон Ома
Ом экспериментально установил закон, согласно которому сила тока, текущего по металлическому проводнику, пропорциональна напряжению на проводнике:
. (2.8)
Обозначенная в формуле (2.8) буквой R величина называется электрическим сопротивлением проводника. Величина сопротивления зависит от размеров и формы проводника, а также от материала, из которого он сделан. Для однородного цилиндрического проводника
, (2.9)
где l -длина проводника, S - площадь его поперечного сечения, r - коэффициент, зависящий от свойств материала проводника и называемый удельным сопротивлением.
Хотя первоначально закон Ома был установлен для однородного участка цепи, то есть участка, не содержащего ЭДС, эта формулировка остается справедливой и для других случаев, если для напряжения применять формулу (2.7).
Однородный участок цепи.
Для участка цепи, на котором сторонние
силы не действуют
напряжение совпадает с изменением
потенциала
и закон Ома принимает вид
.
Неоднородный участок цепи.
Для участка цепи, содержащего ЭДС, формула для напряжения включает как разность потенциалов, так и ЭДС. Поэтому закон Ома можно записать в виде
.
Здесь под R понимается полное сопротивление участка цепи.
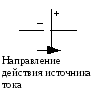Следует
обратить внимание, что ЭДС - величина
алгебраическая, ее знак зависит от
способа включения источника в электрическую
схему. За направление действия ЭДС
принято то направление, в котором
источник повышает потенциал. Если
направление движения по участку цепи
совпадает с направлением действия ЭДС,
то
,
если противоположно, то
.
Замкнутая неразветвленная цепь.
Для
замкнутой цепи
и выражение для закона Ома принимает
вид
,
где под R понимается полное сопротивление всей цепи.
Закон Джоуля-Ленца
При протекании по участку цепи электрического тока электрические и сторонние силы совершают над свободными зарядами работу. Если за время dt по цепи пройдет заряд dq, то работа по перемещению этого заряда в соответствии с (2.6) равна
.
Используя определение силы тока
и закон Ома
,
получим
.
Для неподвижного проводника эта работа в конечном счете идет на его нагревание. Количество теплоты dQ, которое выделяется на резисторе
. (2.10)
Это выражение представляет собой закон Джоуля-Ленца.
Напомним определение мощности, то есть энергии, выделяющейся в проводнике за единицу времени:
. (2.11)
Используя последнее выражение и закон Ома, закону Джоуля-Ленца можно придать вид:
,
, (2.12)
.
2.1.3. Законы Ома и Джоуля-Ленца в дифференциальной форме
Рассмотрим проводник, находящийся в электрическом поле напряженностью Е, по которому течет электрический ток с плотностью j.
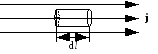В
окрестности некоторой точки проводящей
среды выделим элементарный объем в виде
цилиндра, основания которого площадью
перпендикулярны линиям тока, а образующие
длиной dl
параллельны этим линиям.
Сила тока, протекающего через основания,
равна
,
напряжение на участке составляет
,
сопротивление определяется формулой
.
По закону Ома
.
Подстановка выражений для силы тока,
напряжения и сопротивления в закон Ома
дает выражение
,
из которого после сокращений получаем:
.
Поскольку в изотропной среде направления векторов напряженности и плотности тока совпадают, это выражение можно записать в векторной форме
. (2.13)
Соотношение (2.13) и выражает закон Ома в дифференциальной форме. Оно не содержит дифференциалов, а свое название получило потому, что в нем устанавливается связь между величинами, относящимися к одной и той же точке проводника. Если на рассматриваемом участке действуют сторонние силы, то формула (2.10) принимает вид
.
где
- напряженность поля сторонних сил.
Аналогично можно получить закон Джоуля-Ленца в дифференциальной форме. На основе формулы (2.12) мощность, выделяющаяся в рассматриваемом объеме равна
..
После подстановки силы тока и напряжения иммем
.
С учетом закона Ома
и выражения для объема
последнее выражение принимает вид:
, (2.14)
то есть удельная мощность (мощность, которая выделяется в единице объема проводника) пропорциональна квадрату напряженности электрического поля.