Схемы замещения (эквивалентные схемы) реального иээ

Графическое изображение цепи с помощь. условных обозначений её элементов называется электрической принципиальной схемой.

По принципиальной схеме можно судить о принципе работы цепи, но выполнить её точный расчет нельзя, т.к. каждый элемент цепи, который должен реализовывать соответствующий элемент цепи (параметр), содержит ещё и паразитные элементы.

1. Резистор

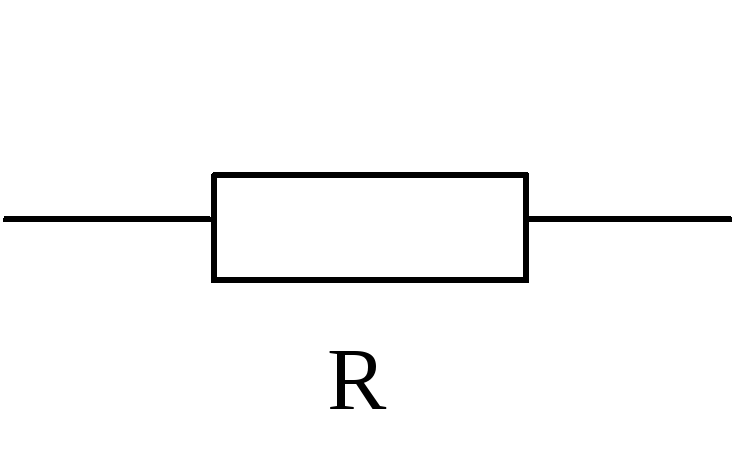
• и 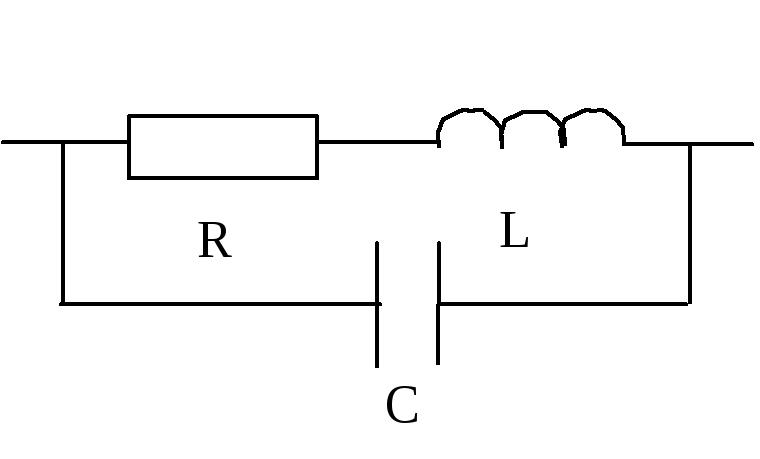деальный элемент

• L – индуктивность и C – емкость являются паразитными элементами в реальном элементе

2. Катушка

3. Конденсатор

Принцип эквивалентности состоит в том, что при замене элемента цепи его эквивалентом оставшаяся цепь не должна ощутить замену, а это значит, что входной ток и входное напряжение между точками подключаемого элемента должны остаться неизменными.

Замечание:

1. Участок цепи на принципиальной схеме, изображенный просто линией, эквивалентен проводнику с активным сопротивлением, равным 0.

R_b,c=0 a и c, b и d имеют одинаковый потенциал

2. При пересечении линий на схеме электрический контакт обозначается точкой.

Схемы замещения ряда иээ

И ЭЭ бывают:

1. Г альванический элемент

2. Источник термоЭДС

3. Источник трехфазного тока

4. Источник постоянного тока

С хемы замещения бывают:

1. с источником тока

(при R_и=0 – потерь нет – идеальный источник тока)

2. с источником напряжения

(при R_и=∞ – потерь нет – идеальный источник напряжения)

Идеальный источник напряжения – это такой ИЭЭ, на полюсах которого напряжение не зависит от сопротивления нагрузки, кроме режима КЗ. У такого источника R_и=0.

Идеальный источник тока – это такой ИЭЭ, ток через полюса которого не зависит от сопротивления нагрузки, кроме режима ХХ. У этого источника R_и=∞.

С физической точки зрения реальный ИЭЭ может быть как идеальным источником напряжения, так и идеальным источником тока.

Реальный источник напряжения – это такой ИЭЭ, на полюсах которого напряжение практически не зависит от сопротивления нагрузки, кроме режима КЗ. У такого источника R_и<<R_н.

Реальный источник тока – это такой ИЭЭ, ток через полюса которого не зависит от сопротивления нагрузки, кроме режима ХХ. У этого источника Rи>>Rн_.

Любой реальный ИЭЭ может быть представлен любой их двух схем замещения!

Два источника можно считать одинаковыми, если у них совпадают 2 из 3 параметров: U_хх – напряжение холостого хода, I_кз – ток короткого замыкания, r – внутреннее сопротивление источника.

1. б)

Устроим режим КЗ на схеме а):

I_кз = Е/R_и

I_хх = 0 → U_abхх = Е, U_R = 0

Для схемы б) I_кз = I, т.к. через резистор R_и ток не идет.

Таким образом обе схемы можно применять.

И ЭЭ характеризуется нагрузочной (или внешней характеристикой) U=f₁(I_н) – зависимость напряжения на полюсах источника от тока нагрузки.

При ↓R_и ↑I → ↑U_Rи → ↓U_н=E-U_Rи

Энергетический баланс эц

Для простоты будем считать, что вся энергия, отданная источником, превращается в тепло. Это значит, что ИЭЭ отдает в нагрузку некоторую мощность.

Мощность, отданная источником: P_н = EI = P_вн + P_н=I² R_вн+I² R_н

Исследуя P_н на экстремум, получаем, что максимальная передача энергии в нагрузку будет осуществляться при R_вн=R_н (режим согласования по мощности) → чем больше R_н, тем больше η.