- •24 Декабря 2009 г.
- •Задание на курсовую работу
- •Вариант 1
- •Задание на курсовую работу
- •Вариант 2
- •Задание на курсовую работу
- •Вариант 3
- •Задание на курсовую работу
- •Вариант 4
- •Задание на курсовую работу
- •Вариант 5
- •Задание на курсовую работу
- •Вариант 6
- •Задание на курсовую работу
- •Вариант 7
- •Задание на курсовую работу
- •Вариант 8
- •Задание на курсовую работу
- •Вариант 9
- •Задание на курсовую работу
- •Вариант 10
- •Задание на курсовую работу
- •Вариант 11
- •Задание на курсовую работу
- •Вариант 12
- •Задание на курсовую работу
- •Вариант 13
- •Задание на курсовую работу
- •Вариант 14
- •Задание на курсовую работу
- •Вариант 15
- •Задание на курсовую работу
- •Вариант 16
- •Задание на курсовую работу
- •Вариант 17
- •Задание на курсовую работу
- •Вариант 18
- •Задание на курсовую работу
- •Вариант 19
- •Задание на курсовую работу
- •Вариант 20
Министерство образования и науки Российской Федерации
Архангельский государственный технический университет
ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
Методическое пособие
к выполнению курсовой работы
Архангельск
2010
Рассмотрено и рекомендовано к изданию методической комиссией
химико-технологического факультета
Архангельского государственного технического университета
24 Декабря 2009 г.
Рецензенты
Ю.И. Берлин, ст. преп., кафедры бухгалтерского учета, аудита и статистики, канд. экон. наук, Всероссийский заочный финансово-экономический институт
А.Н. Шкаев, доцент, канд. хим. наук, Архангельский государственный технический университет
Планирование эксперимента: методическое пособие к выполнению курсовой работы [Текст] / авт. – сост. С.А. Кабаков. – Архангельск: Арханг. гос. техн. ун-т, 2010. – 101 c.
Подготовлено на кафедре “Стандартизация, метрология и сертификация”.
Выполнение курсовой работы по дисциплине “Планирование и организация эксперимента” позволит получить навыки при планировании эксперимента с расчетом реализованного полного факторного плана, получением уравнения регрессии, проверки его адекватности и построением поверхности отклика. В методическом пособии приведены некоторые теоретические положения, а также показан пример выполнения курсовой работы.
© Архангельский государственный
технический университет, 2010
ОГЛАВЛЕНИЕ
|
ВВЕДЕНИЕ………………………………………………………… |
5 |
|
1 ОСНОВНЫЕ ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ…………………. |
6 |
|
2 ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА………………………… |
8 |
|
2.1 Факторы……………………………………………………… |
9 |
|
2.2 Выбор уровней варьирования факторов и основного уровня |
10 |
|
2.3 Система “черный ящик” …………………………………… |
13 |
|
2.4 Определение значимости коэффициентов регрессии……. |
16 |
|
3 СТАТИСТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА …………………………………………… |
18 |
|
3.1 Выявление грубых погрешностей ………………………... |
29 |
|
3.2 Полигон и гистограмма частот распределения ………….. |
30 |
|
4 ПРИМЕР ДЛЯ ВЫПОЛНЕНИЯ КУРСОВОЙ РАБОТЫ……… |
34 |
|
4.1 Первичная обработка………………………………………... |
34 |
|
4.2 Определение доверительного интервала…………………... |
38 |
|
4.3 Проверка гипотезы о нормальности распределения результатов измерений………………………………………….. |
41 |
|
5 РАСЧЕТЫ ПО ПЛАНИРОВАНИЮ ПОЛНОГО ФАКТОРНОГО ЭКСПЕРИМЕНТА……………………………...……………. |
43 |
|
5.1 Расчет реализованного плана полного факторного эксперимента (ПФП)…………………………………………………… |
43 |
|
5.2 Расчет коэффициентов уравнения регрессии ……………… |
46 |
|
5.3 Определение значимости коэффициентов регрессии……… |
48 |
|
5.4 Проверка уравнения на адекватность………………………. |
45 |
|
5.5 Приведение уравнения регрессии к натуральным значениям |
50 |
|
5.6 Построение поверхности отклика………………………..... |
51 |
|
ПРИЛОЖЕНИЕ А Квантили распределения Стьюдента t(p,f) .. |
53 |
|
ПРИЛОЖЕНИЕ Б Значение f2(t) – распределение Пирсона …… |
54 |
|
ПРИЛОЖЕНИЕ В Значения функции Лапласа………………… |
55 |
|
ПРИЛОЖЕНИЕ Г Квантили распределения Фишера ……… |
58 |
|
ПРИЛОЖЕНИЕ Д Квантили распределения Кохрана………. |
59 |
|
Варианты для выполнения курсовой работы…………………….... |
60 |
ВВЕДЕНИЕ
Эксперименты, как правило, являются многофакторными и связаны с оптимизацией качества материалов, отысканием оптимальных условий проведения технологических процессов, параметров оборудования и т.д. Объекты таких исследований зачастую представляют собой сложную систему, поэтому, несмотря на значительный объем выполненных исследовательских работ невозможно достаточно полно изучить данный объект. В связи с этим многие решения основаны на информации, имеющей случайный характер, и поэтому отличаются от истинных значений.
Традиционные методы исследований связаны с экспериментами, которые требуют больших затрат, сил и средств, так как основаны на поочередном варьировании отдельных независимых переменных при сохранении остальных в неизменном виде.
В шестидесятые годы прошлого столетия появилось новое направление в планировании эксперимента, связанное с оптимизацией процессов – планирование экстремального эксперимента. Первая работа в этой области была опубликована в начале 50-х годов английскими учеными Боксом и Уилсоном. Они предложили последовательно ставить небольшие серии опытов, в каждой из которых одновременно изменяются (варьируются) по определенным правилам все факторы. Серии опытов проводят таким образом, чтобы после математической обработки предыдущей можно было спланировать следующую серию опытов. Так последовательно, шаг за шагом, достигается область оптимума.
Планирование эксперимента делает поведение экспериментатора целенаправленным и организованным, существенно способствует повышению производительности труда и надежности полученных результатов. Важным достоинством является его универсальность, возможность применения в большинстве областей исследований.
1 ОСНОВНЫЕ ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ
Объект исследования – материал, продукция, оборудование или технологический процесс.
Теория – совокупность положений, объясняющие общим принципом какие-либо факты, дающие возможность открывать и объяснять новые факты.
Фактор – переменная величина, по предположению влияющая на результаты эксперимента.
Эксперимент – система операций, воздействий и (или) наблюдений, направленных на получение информации об объекте при исследовательских испытаниях.
Опыт – воспроизведение исследовательского явления в определённых условиях проведения эксперимента при возможности регистрации его результатов.
Математическая статистика – наука о математических методах получения, систематизации, обработки, анализа и использования статистических данных для научных и практических выводов. Математическая статистика опирается на теорию вероятности, которая дает возможность оценить надежность и точность выводов, сделанных на основе ограниченного статистического материала.
План эксперимента – совокупность данных, определяющих число, условия и порядок реализации планов.
Активный эксперимент – эксперимент, в котором уровни факторов в каждом опыте задаются исследователем.
Пассивный эксперимент – эксперимент, при котором уровни факторов в каждом опыте регистрируются исследователем, но не задаются.
Последовательный эксперимент – эксперимент, реализуемый в виде серий, в котором условия проведения каждой последующей серии определяются результатами предыдущих.
Отклик – наблюдаемая случайная переменная, по предположению, зависящая от факторов.
Функция отклика – зависимость математического ожидания отклика от факторов.
Поверхность отклика – геометрическое представление функции отклика.
Модель регрессионного анализа – зависимость отклика от количественных факторов и ошибок наблюдения отклика.
Адекватность математической модели – соответствие математической модели экспериментальным данным по выбранному критерию.
Коэффициент регрессии – параметр модели регрессионного анализа.
Точка плана – упорядоченная совокупность числовых значений факторов, соответствующая условиям проведения опыта.
Центральная точка опыта – точка опыта, соответствующая нулям нормализованной (безразмерной) шкалы по всем факторам.
Звёздная точка плана – точка плана второго плана, лежащая на координатной оси в факторном пространстве.
Матрица плана – стандартная форма записи условий проведения экспериментов в виде прямоугольной таблицы, строки которой отвечают опытам, столбцы - факторам.
Полный факторный план – план, содержащий все возможные комбинации всех факторов на определённом числе уровней равное число раз.
Дробный факторный эксперимент – план, содержащий часть комбинаций полного факторного плана.
Регрессионный анализ – статистический метод анализа и обработки экспериментальных данных при воздействии на отклик только количественных факторов, основанный на сочетании аппарата метода наименьших квадратов и техники статистической проверки гипотез.
Дисперсионный анализ – статистический метод анализа и обработки экспериментальных данных при воздействии на отклик только количественных факторов, основанный на использовании техники статистической проверки гипотез и представлений и общей вариации экспериментальных данных в виде суммы вариации, обусловленных исследуемыми факторами и их взаимодействиями.
2 ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
Планирование эксперимента – это наиболее эффективное (оптимальное) управление ходом эксперимента для получения максимально возможной информации на основе минимально допустимого количества опытов.
Эксперимент, в котором исследователь по своему усмотрению может изменять условия его проведения, называют активным экспериментом. В противном случае эксперимент является пассивным.
Перед планированием активного эксперимента собирают предварительную (априорную) информацию об исследуемом объекте. Для получения такой информации используют результаты экспериментов, проводимых в предыдущих исследованиях или описанных в литературных источниках. Планирование эксперимента позволяет варьировать всеми факторами и получать одновременно оценки их влияния. В случае статистического подхода математическую модель объекта или процесса представляют в виде полинома, т.е. отрезка ряда Тейлора, в который разлагается неизвестная функция:
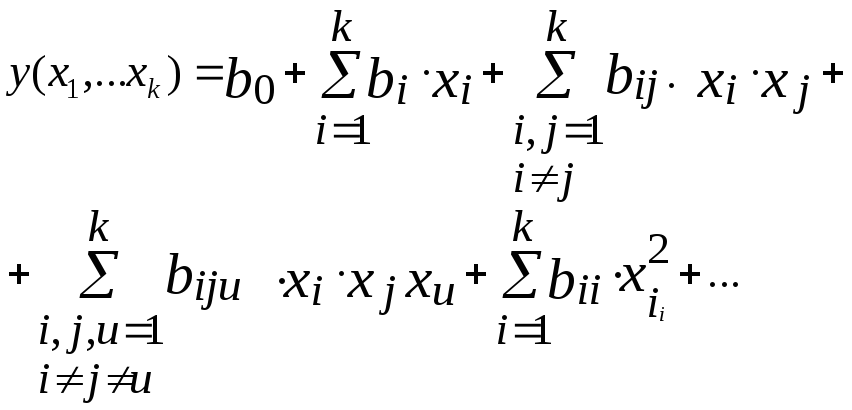 (2.1)
(2.1)
где b0 - свободный член;
bi - линейные эффекты;
bij - эффекты парного взаимодействия;
biju - эффекты тройного взаимодействия.
2.1 Факторы
После выбора объекта исследования и параметра оптимизации устанавливают все факторы, которые могут влиять на выбранный объект. Если какой-либо существенный фактор в ходе эксперимента принимал произвольные значения, не контролируемые экспериментатором, то в результате значительно возрастет ошибка опыта. Поддержание такого фактора на определенном уровне приведет к ложному представлению об оптимуме, т.к. не гарантирует оптимальности полученного уровня.
Фактором называют измеряемую переменную величину, принимающую в некоторый момент времени определенное значение и влияющую на объект исследования.
Факторы должны иметь область определения, внутри которой задают его конкретные значения. Область определения может быть непрерывной или дискретной. При планировании эксперимента значения факторов дискретные, что связано с уровнями факторов. В практических задачах области определения факторов имеют ограничения, которые носят либо принципиальный, либо технический характер.
Факторы бывают количественными и качественными.
Факторы должны быть управляемыми, что означает возможность поддерживания нужного значения фактора на постоянном уровне в течение всего опыта. Планировать эксперимент можно только в том случае, если уровни факторов может задавать экспериментатор.
Например, эксперименты проводят на открытой площадке. В этом случае невозможно управлять температурой воздуха, ее можно только контролировать, и потому при выполнении опытов температуру, как фактор, не учитывают.
Точность замеров факторов должна быть максимально высокой, при этом степень точности зависит от диапазона изменения факторов. В длительных процессах, измеряемых многими часами, минуты не учитывают, а в быстрых процессах учитывают даже доли секунды.
Факторы должны быть однозначны. Трудно управлять фактором, который является функцией других факторов. Однако в планировании могут участвовать другие факторы, такие, как соотношения между компонентами, их логарифмы и т.п.
При планировании эксперимента одновременно изменяют несколько факторов, поэтому необходимо знать требования к совокупности факторов. Прежде всего, факторы должны быть совместимы, что означает осуществимость и безопасность всех их комбинаций.
Несовместимость факторов наблюдается на границах областей их определения, а избавиться от нее можно сокращением этих областей. Положение усложняется, если несовместимость проявляется внутри областей определения. В этом случае одно из возможных решений – разбиение на подобласти и решение двух отдельных задач.
При планировании эксперимента важна независимость факторов, т.е. возможность установления фактора на любом уровне вне зависимости от уровней других факторов. Если это условие невыполнимо, то невозможно планировать эксперимент.
2.2 Выбор уровней варьирования факторов и основного уровня
Фактор считают заданным, если указаны его название и область определения. В выбранной области определения он может иметь несколько значений, которые соответствуют числу его различных состояний. Выбранные для эксперимента количественные или качественные состояния фактора называют уровнями фактора.
В планировании эксперимента значения факторов, соответствующие определенным уровням их варьирования, выражают в кодированных величинах. Под интервалом варьирования фактора понимают разность между двумя его значениями.
При выборе области определения факторов особое внимание уделяют выбору нулевой точки, или нулевого (основного) уровня. Выбор нулевой точки эквивалентен определению исходного состояния объекта исследования. Оптимизация связана с улучшением состояния объекта по сравнению с состоянием в нулевой точке. Поэтому желательно, чтобы данная точка была в области оптимума или как можно ближе к ней, тогда можно ускорить поиск оптимальных решений.
Если проведению эксперимента предшествовали другие исследования по рассматриваемому вопросу или проведен анализ имеющихся литературных данных (получение априорной информации), то за нулевую принимают точку, которой соответствует наилучшее значение параметра оптимизации, установленного в результате формализации априорной информации.
Если при постановке задачи область определения факторов задана, то центр этой области принимают за нулевую точку. Например, если в некоторой задаче фактор W (влажность) изменяется от 10 до 60 %. , то за нулевой уровень принимают среднее значение фактора, соответствующее 35 %.
После установления нулевой точки выбирают интервалы варьирования факторов. Это связано с определением таких значений факторов, которые в кодированных величинах соответствуют “+1” и “–1”. Интервалы варьирования выбирают с учетом того, что значения факторов, соответствующие уровням “+1” и “–1”, должны в достаточной степени отличаться от значения, соответствующему нулевому уровню. Поэтому во всех случаях величина интервала варьирования должна быть больше удвоенной квадратичной ошибки фиксирования данного фактора. С другой стороны, чрезмерное увеличение величины интервалов варьирования нежелательно, т.к. это может привести к снижению эффективности поиска оптимума, а очень малый интервал варьирования уменьшает область эксперимента, что замедляет поиск оптимума.
При выборе интервала варьирования целесообразно учитывать, если это возможно, число уровней варьирования факторов в области эксперимента. От числа уровней зависят объем эксперимента и эффективность оптимизации.
В общем виде зависимость числа опытов от числа уровней факторов имеет вид
N=pk, (2.2)
где N – число опытов;
р – число уровней факторов;
k – число факторов.
Минимальное число уровней, применяемое на первой стадии эксперимента, равно 2. Это верхний и нижний уровни, обозначаемые в кодированных координатах через “+1” и “–1”. Варьирование факторов на двух уровнях используют в отсеивающих экспериментах, на стадии движения в область оптимума и при описании объекта исследования линейными моделями. Но такое число уровней недостаточно для построения моделей второго порядка (если фактор принимает только два значения, то через две точки можно провести множество линий различной кривизны).
С увеличением числа уровней повышается чувствительность эксперимента, но одновременно возрастает число опытов. При построении моделей второго порядка используют 3, 4 или 5 уровней, причем здесь наличие нечетных уровней указывает на проведение опытов в нулевых (основных) уровнях.
В каждом отдельном случае число уровней выбирают с учетом условий задачи и предполагаемых методов планирования эксперимента.
Необходимо учитывать наличие качественных и дискретных факторов. В экспериментах, связанных с построением линейных моделей, наличие этих факторов, как правило, не вызывают дополнительных трудностей. При планировании второго порядка качественные факторы не применимы, т.к. они не имеют ясного физического смысла для нулевого уровня. Для дискретных факторов часто применяют преобразование измерительных шкал, чтобы обеспечить фиксацию значений факторов на всех уровнях.
После выбора объекта исследования и параметра оптимизации оценивают все факторы, которые могут влиять на объект. Если какой-либо существенный фактор окажется неучтенным, принимающим произвольные значения, не контролируемые экспериментатором, то это существенно увеличит ошибку опыта. При поддержании этого фактора на определенном уровне может быть получено ложное представление об оптимуме, т.к. нет гарантии, что полученный уровень является оптимальным.
С другой стороны большое число факторов увеличивает число опытов и размерность факторного пространства. Итак, выбор факторов является весьма существенным, т.к. от этого зависит успех оптимизации.
2.3 Система “черный ящик”
Объект исследования можно представить в виде системы “черный ящик” (рисунок 2.1). Суть такой системы состоит в изучении зависимости отклика системы Y на изменение входных измеряемых и управляемых параметров (факторов) X(x1, x2,..., xk) при действии случайных факторов W(w1,w2,..., wn), которые называют возмущающими эффектами объекта. Параметры Х называют основными, определяющими условия эксперимента. Выходным параметром (откликом) Y могут быть любые технологические или технические показатели исследуемого процесса. Случайным будет считаться любой фактор, не вошедший в основной комплекс входных параметров.
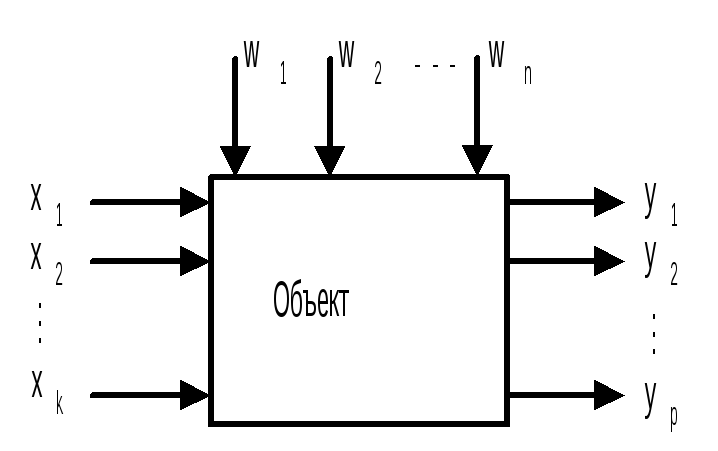
Рисунок 2.1 – Система “черный ящик”
При описании области, близкой к экстремуму, чаще других применяют полиномы второго порядка, что связано в первую очередь с тем, что полиномы второго порядка легко поддаются систематизации и исследованию на экстремум. При этом число опытов N должно быть не меньше числа определяемых коэффициентов в уравнении регрессии второго порядка для k факторов.
На практике функцию (2.1) строят в виде полинома
![]() .
(2.3)
.
(2.3)
После выбора линейной модели для построения аппроксимирующей функции выбирают основной уровень и интервал варьирования для каждого фактора. Для линейной модели интервал варьирования определяют
![]() ,
(2.4)
,
(2.4)
где Xi max, Xi min – значения факторов на верхнем и нижнем уровнях.
Основной (нулевой) уровень определяют
![]() .
(2.5)
.
(2.5)
Для упрощения планирования эксперимента вместо реальных (натуральных) уровней факторов используют кодированные значения факторов. Эту операцию называют нормализацией.
![]() ,
(2.6)
,
(2.6)
где xi – нормализованное значение переменного фактора;
![]() ,
,
![]() – натуральные значения факторов.
– натуральные значения факторов.
Рассмотрим полный факторный план (ПФП) линейной модели (2.1) при числе факторов k = 2. Для проведения полного факторного эксперимента необходимо провести N = 2k опытов, где 2 – число уровней факторов.
Условие проведения такого эксперимента можно записать в виде матрицы.
-
Номер серии опытов
x1
x2
x1.x2
yj
1
-1
-1
+1
y1
2
+1
-1
-1
y2
3
-1
+1
-1
y3
4
+1
+1
+1
y4
Коэффициенты регрессии рассчитывают по формулам
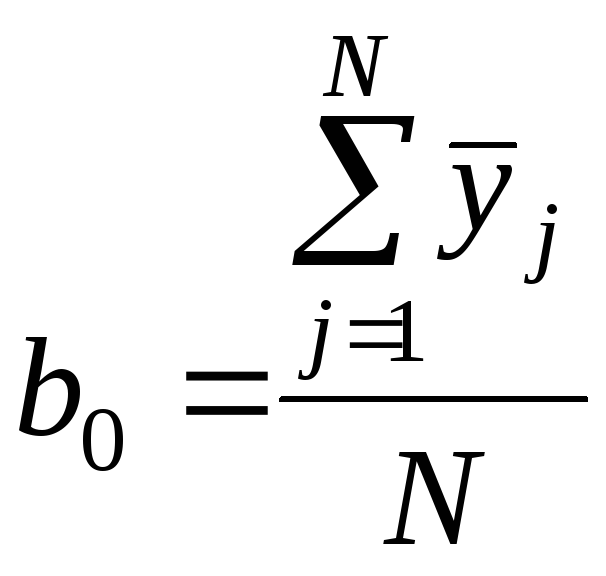 ,
(2.7)
,
(2.7)
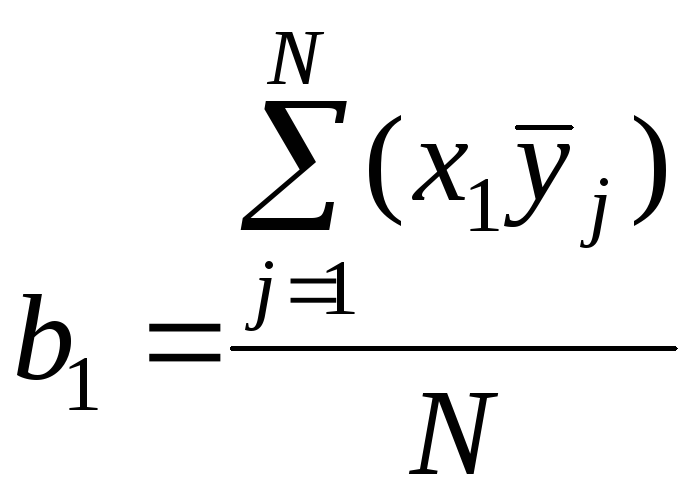 ,
(2.8)
,
(2.8)
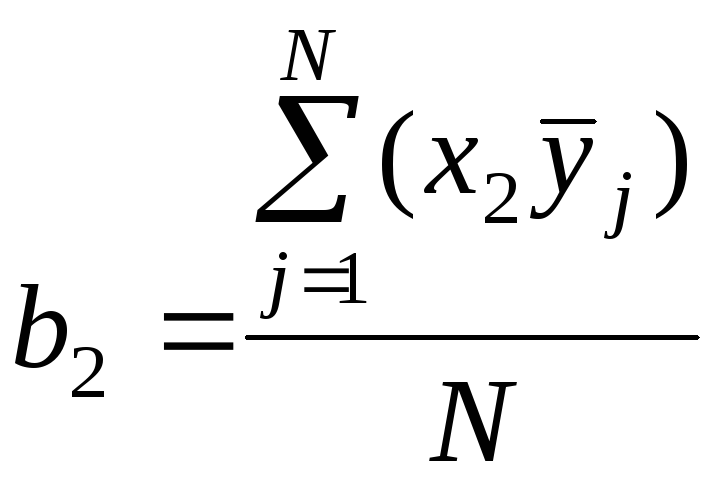 ,
(2.9)
,
(2.9)
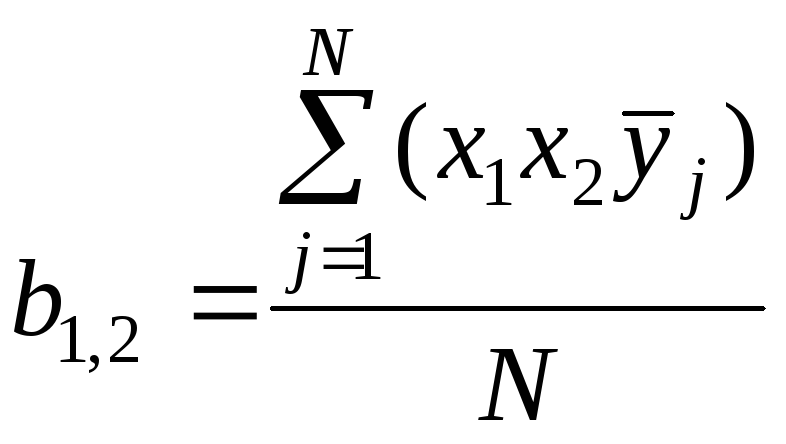 .
(2.10)
.
(2.10)
2.4 Определение значимости коэффициентов регрессии
В планах ПФП дисперсии коэффициентов при линейных членах и членах, характеризующих взаимодействие различных порядков, равны, что упрощает оценку значимости коэффициентов. Коэффициенты считают значимыми, если выполняется условие
![]() ,
(2.11)
,
(2.11)
где
![]() - дисперсия коэффициентов регрессии;
- дисперсия коэффициентов регрессии;
![]() – коэффициент
Стьюдента (приложение 1),
– коэффициент
Стьюдента (приложение 1),
при p = 0,05 и f = N (n – 1));
f – число степеней свободы;
n – число повторных опытов;
N – число серий опытов.
Дисперсию коэффициентов регрессии рассчитывают
![]() (2.12)
(2.12)
где
![]() _
дисперсия воспроизводимости выходного
параметра,
_
дисперсия воспроизводимости выходного
параметра,
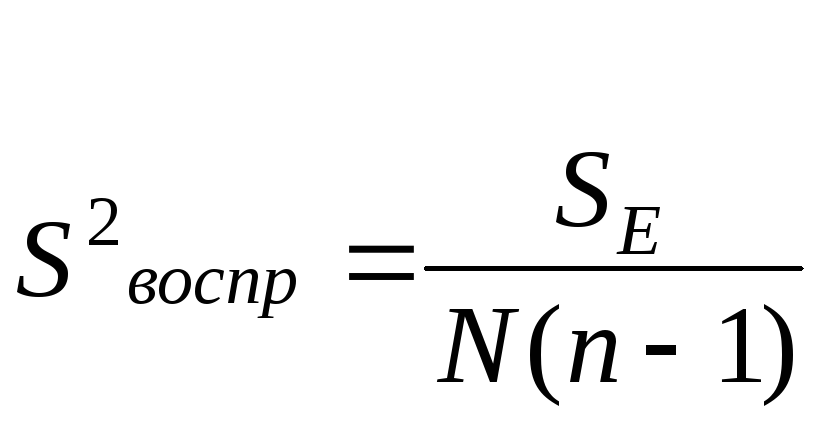 ,
(2.13)
,
(2.13)
где
![]() - сумма построчных дисперсий.
- сумма построчных дисперсий.
![]() =
=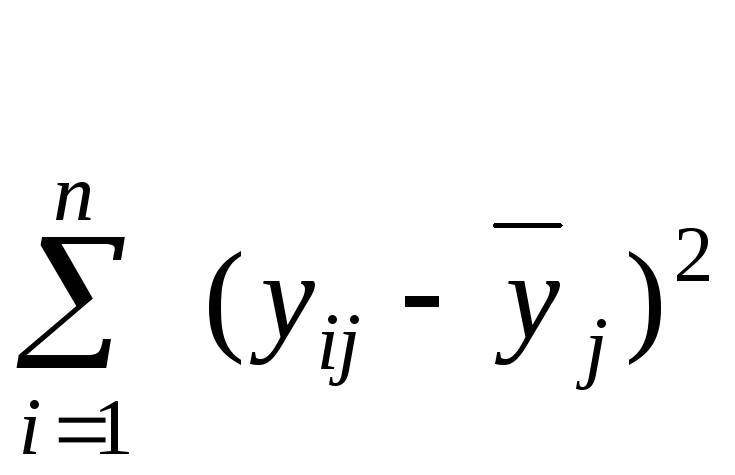 ,
(2.14)
,
(2.14)
где
![]() - значение выходной величины в i-ом
дублированном опыте j-
ой серии;
- значение выходной величины в i-ом
дублированном опыте j-
ой серии;
![]() -
среднее
арифметическое повторных опытов.
-
среднее
арифметическое повторных опытов.
Среднее арифметическое повторных опытов определяют
![]() .
(2.15)
.
(2.15)
Следующим этапом оценивают воспроизводимость экспериментальных данных по критерию Кохрана (приложение Г).
![]() ,
(2.16)
,
(2.16)
где S2j max – максимальное значение дисперсии серий опытов.
Если
![]() <
<
![]() ,
то опыты воспроизводимы (статистически
однородны), если
,
то опыты воспроизводимы (статистически
однородны), если
![]() – необходимо принять при проведении
исследования более точные методы и
средства измерения.
– необходимо принять при проведении
исследования более точные методы и
средства измерения.
Проверку уравнения на адекватность проводят по критерию Фишера, расчетное значение которого находят:
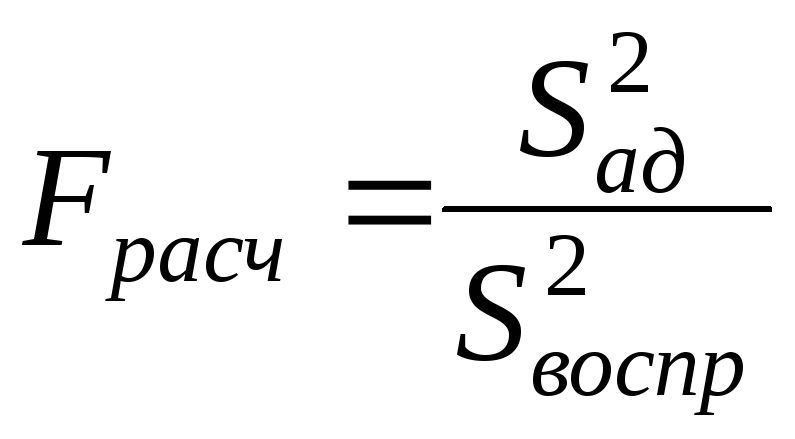 ,
(2.17)
,
(2.17)
где
![]() – дисперсия адекватности;
– дисперсия адекватности;
![]() – дисперсия
воспроизводимости.
– дисперсия
воспроизводимости.
Дисперсию адекватности рассчитывают
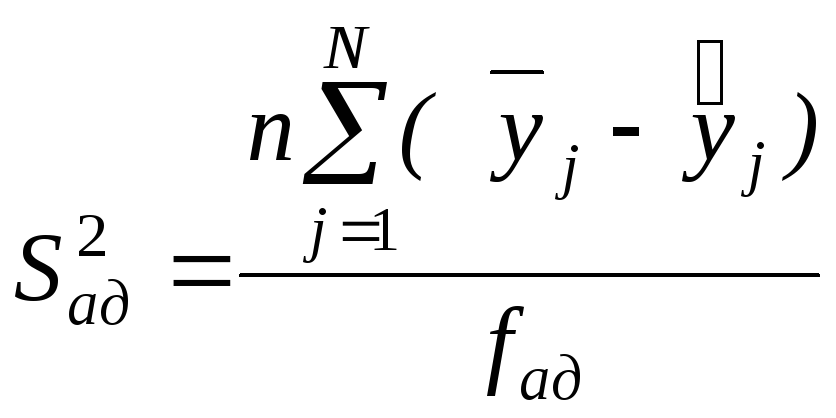 ,
(2.18)
,
(2.18)
где
![]() –
расчетные значения выходной величины;
–
расчетные значения выходной величины;
fад. – число степеней свободы , равно N – m;
m – число значимых коэффициентов уравнения регрессии с учетом свободного члена.
Расчетное значение сравнивают с критерием Фишера, принимаемым по таблице (приложение Д). Если Fрасч < Fтабл , то уравнение адекватно.
3 СТАТИСТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА
Научные исследования основаны на принципах системного и научного подходов.
При системном подходе исследуемый объект представляют как совокупность некоторого числа взаимосвязанных элементов (систем), являющихся одновременно подсистемами некоторых более сложных систем, что позволяет исследовать все аспекты взаимосвязей между ними.
Научный подход предполагает использование при обработке результатов исследований теории вероятностей и математической статистики.
Результаты измерений при экспериментальных исследованиях представляют собой единичные измерения (yi), которые являются случайными величинами, принимающими в результате испытания заранее неизвестные числовые значения, зависящие от случайного исхода испытаний.
Случайные величины могут быть:
дискретными, принимающими конечное множество значений, отдаленных друг от друга и которые можно пронумеровать (например, количество дефектных деталей);
непрерывными, возможные значения, которых заполняют какой-то промежуток.
При изучении свойств объекта исследований путем измерения и регистрации количественных значений этих свойств получают множество значений случайной величины или статистическую совокупность.
Совокупность, которая содержит все возможные значения исследуемого свойства объекта, полученные при данных условиях эксперимента, называют генеральной совокупностью.
Обычно имеют дело с частью генеральной совокупности называемой выборочной совокупностью (выборкой).
Получение абсолютно точных измерений невозможно из-за ошибок, поэтому при проведении эксперимента одной из основных задач является оценка ошибок, выполняемая с помощью математической статистики.
Воздействие помех на процесс измерения приводит к тому, что результаты измерения всегда отличаются от истинного значения измеряемой величины и по этим результатам определить истинное значение нельзя. Разность между результатом измерения и истинным значением называется истинной погрешностью измерения. В силу того что истинное значение неизвестно, неизвестной является и истинная погрешность.
Учитывая, что ни истинное значение физической величины, ни истинную погрешность в опыте определить невозможно, задачу нахождения истинного значения формулируют как задачу нахождения некоторого приближенного значения с указанием диапазона возможных отклонений этого приближенного значения от истинного значения. Найденное в эксперименте значение измеряемой величины, приближенное к истинному значению, называется оценкой физической величины. Оценка с указанием ее возможного интервала отклонения от истинного значения называют результатом измерения.
Погрешность измерения включает в себя множество различных составляющих, которые классифицируют по различным признакам, включающим около 30 видов.
Погрешности измерения подразделяют:
а) по виду влияния на результаты – систематические и случайные;
б) по характеру изменения во времени – статические и динамические;
в) по источникам возникновения – методические, инструментальные, погрешности оператора. Эти погрешности, в свою очередь, могут быть как случайными, так и систематическими. По возможности выявления и исключения из результатов измерения погрешности подразделяют: выявленные и невыявленные, устранимые и неустранимые, исключенные и неисключенные;
г) по характеру принадлежности (близости) результатов наблюдений к основной совокупности выделяют грубые погрешности и промахи.
Невыявленные погрешности всегда неустранимы. Выявленная погрешность может быть как устранимой, так и неустранимой. Например, случайная погрешность, а также систематическая погрешность известной величины, но неизвестного знака, имеют определенные числовые значения, т. е. относятся к разряду выявленных. Тем не менее, они не могут быть устранены (исключены из результатов), т. е. являются неустранимыми.
Систематическая погрешность – это составляющая погрешности измерения, которая остается постоянной или закономерно изменяется при повторных измерениях.
Одной из основных задач обработки результатов эксперимента является выявление, оценка величины и, по возможности, устранение всех систематических погрешностей. Изменяющиеся систематические погрешности выявляются легче, чем постоянные погрешности. Для выявления постоянной систематической погрешности необходимо выполнить измерения, например, двумя различными методами. Обнаруженные и оцененные систематические погрешности исключают из результатов путем введения поправок.
В зависимости от причин возникновения систематические погрешности подразделяют на следующие виды:
– погрешности метода или модели, которые обычно называют методическими погрешностями, например: определение плотности вещества без учета имеющихся в нем примесей, использование формул, не совсем точно описывающих явление, и др.;
– погрешности воздействия внешних факторов: внешних тепловых, радиационных, гравитационных, электрических и магнитных полей;
– погрешности, возникающие из-за неточности действий или личных качеств оператора (экспериментатора), называемые личностными погрешностями;
– инструментальные (приборные, аппаратурные) погрешности, обусловленные схемными, конструктивными и технологическими несовершенствами средств измерения, их состоянием в процессе эксплуатации. Например, смещение начала отсчета, неточность градуировки шкалы прибора, использование прибора вне допустимых пределов его эксплуатации, неправильное положение прибора и т. п. За исключением смещения начала отсчета, приборные погрешности относят к разряду неустранимых погрешностей.
В общем случае систематическая погрешность обусловлена суммарным воздействием перечисленных факторов, многие из которых невозможно рассчитать, исключить или выявить в данном эксперименте. Самым простым способом выявления суммарной систематической погрешности было бы сопоставление результатов измерений, полученных с помощью серийного (рабочего) и более точного образцового приборов. Разность результатов измерений даст суммарную систематическую погрешность, вносимую серийным прибором в результат измерения. Однако такой способ выявления систематической погрешности является слишком дорогим. Поэтому на практике различные составляющие систематической погрешности устраняют с помощью экспериментальных или математических приемов путем введения поправок в результаты наблюдений при условии, что погрешность данного вида по величине и знаку известна. После внесения поправок влияние систематической погрешности данного вида на результат и погрешность измерения устраняется полностью. Если же систематическая погрешность неизвестна, но имеет известные границы изменения, то её учитывают в результате измерения.
Случайная погрешность – это составляющая погрешности измерения, проявляющаяся в виде непредсказуемых отклонений от истинного значения физической величины, меняющихся от одного наблюдения к другому. Данная погрешность обусловлена влиянием на результаты измерения множества факторов, воздействие которых на каждое отдельное измерение невозможно учесть или заранее предсказать. Такими причинами могут быть перепады напряжения в сети, вибрация установки, изменения атмосферного давления, влажности, температуры, а также ошибки, связанные с действиями самого экспериментатора (неправильное считывание показаний приборов, различная скорость реакции и т. п.). Случайную погрешность нельзя исключить из результатов измерений, однако, пользуясь статистическими методами, можно учесть ее влияние на оценку истинного значения измеряемой величины.
Грубая погрешность – погрешность измерения, значительно превышающая погрешности большинства результатов наблюдений. Такие погрешности могут возникать вследствие резкого изменения внешних условий эксперимента. Грубые погрешности обнаруживают статистическими методами и соответствующие результаты измерений, как не отражающие закономерностей поведения измеряемой величины, исключают из рассмотрения.
Промах – это вид грубой погрешности, зависящий от наблюдателя и связанный с неправильным обращением со средствами измерений: неверными отсчетами показаний приборов, описками при записи результатов, невнимательностью экспериментатора, путаницей номеров образцов и т. п. Промахи обнаруживают нестатистическими методами и результаты наблюдений, содержащие промахи, как заведомо неправильные, исключают из рассмотрения.
Указанные составляющие, как правило, не зависят друг от друга, что допускает их раздельное рассмотрение.
Полная погрешность измерения, являющаяся суммой указанных составляющих, может быть представлена в абсолютном и относительном виде.
Абсолютная погрешность – это погрешность измерения, выраженная в единицах измеряемой величины. Наряду с абсолютной погрешностью часто используется термин абсолютное значение погрешности, под которым понимают значение погрешности без учета ее знака. Эти два понятия различны.
Относительная погрешность – это погрешность измерения, выраженная отношением абсолютной погрешности к результату измерения.
Относительная погрешность являются безразмерной величиной и ее выражают в процентах.
Числовой
характеристикой погрешности является
доверительный интервал, в котором с
заданной доверительной вероятностью
(Р)
находится погрешность измерения (![]() ).
При доверительной вероятности
).
При доверительной вероятности
![]() ,
статистический вывод будет справедлив
в 95 случаях из 100.
,
статистический вывод будет справедлив
в 95 случаях из 100.
Для практических целей используют величину р, называемую уровнем значимости
р =1 – P. (3.1)
Большинство статистических оценок предполагает нормальное (или Гауссово) распределение результатов измерений.
Если на основании наблюдений некоторого непрерывного показателя построить распределение частот, то обычно оно представляет собой симметричную (нормальную) кривую – кривую нормального распределения. Подобную форму кривой имеют, например результаты повторных измерений показателей качества продукции.
Уравнение кривой нормального распределения определяют выражением
![]() ,
(3.2)
,
(3.2)
где у – плотность вероятности некоторого значения переменной х;
а и b – коэффициенты.
С увеличением коэффициента а, кривая "вытягивается " в высоту, а при увеличении коэффициента b – кривая "сплющивается".
Нормальное распределение определяют двумя параметрами: генеральное среднее M y, которое характеризует положение центра группирования результатов на числовой оси, и генеральная дисперсия или рассеивание результатов относительно M y.
Кривая
симметрична относительно среднего
значения M
y
и
имеет две точки перегиба с координатами:
y
=![]() (рисунок 3.1).
(рисунок 3.1).

Рисунок 3.1 – Стандартные отклонения и точки перегиба при нормальном распределении
С
помощью кривых нормального распределения
можно установить частоту появления
ошибки той или иной величины. Вероятность
попадания результата измерения в
интервал
![]() равна 68,27 %; в интервал
равна 68,27 %; в интервал
![]() равна
95,45 %; а в интервал
равна
95,45 %; а в интервал
![]() –
99,73 %. Таким образом, интервал
–
99,73 %. Таким образом, интервал
![]() можно считать предельным отклонением
или полем рассеяния.
можно считать предельным отклонением
или полем рассеяния.
При повторении (дублировании) опытов в одинаковых условиях можно заметить, что некоторые значения случайной величины встречаются значительно чаще других и группируются относительно некоторого центра.
Характеристикой
центра группирования случайной величины
является
математическое
ожидание
или
генеральное
среднее
(![]() ).
).
Следует отметить, что только математическое ожидание не может отобразить все особенности статистической совокупности, поэтому необходимо установить изменчивость, или вариацию характеристики явления.
Степень рассеивания случайной величины относительно математического ожидания характеризует генеральная дисперсия
![]() .
(3.3)
.
(3.3)
Среднеквадратическое отклонение случайной величины характеризует рассеивание результатов относительно математического ожидания
![]() .
(3.4)
.
(3.4)
При
обработке данных, полученных при
исследованиях, оперируют не генеральной,
а выборочной совокупностью, т. е.
используют статистики
приближенно оценивающие M
y
и
![]() .
.
Наилучшей
оценкой M
y
является
среднее арифметическое выборки
(![]() )
)
![]() .
(3.5)
.
(3.5)
Среднее арифметическое выборки определяет центр распределения случайной величины и имеет ту же размерность, что и изучаемый параметр.
Оценкой
дисперсии
2
является выборочная или эмпирическая
дисперсия (![]() )
)
![]() (3.6)
(3.6)
Эти
оценки являются состоятельными и
несмещенными для выборки из нормальной
совокупности при
![]() .
.
Несмещённость
оценки
![]() достигается использованием в знаменателе
формулы (3.6) величины, называемой числом
степеней свободы f
достигается использованием в знаменателе
формулы (3.6) величины, называемой числом
степеней свободы f
![]() .
(3.7)
.
(3.7)
Потеря одной степени свободы при вычислении выборочной дисперсии необходима для вычисления среднего значения. В общем случае число степеней свободы равно количеству независимых измерений, участвующих в определении того или иного параметра статистической совокупности.
Степень разброса случайных величин вокруг среднего значения характеризуют выборочная дисперсия и среднее квадратическое отклонение S
 . (3.8)
. (3.8)
Для
характеристики того, насколько среднее
арифметическое хорошо представляет
статистический ряд используют коэффициент
вариации. Коэффициент
вариации V
(в процентах) является мерой относительной
изменчивости (вариации) случайной
величины относительно среднего значения
![]()
![]() .
(3.9)
.
(3.9)
Чем меньше коэффициент вариации, тем меньше среднее рассеяние значений параметра вокруг среднего арифметического. Если сравнивают два ряда, имеющие одинаковое среднее арифметическое, то среднее арифметическое ряда с меньшим коэффициентом вариации более представительно. Если коэффициент вариации V < 33%, то можно проводить проверку нормальности распределения.
Для характеристики надежности результатов наблюдений используют следующие показатели.
Среднюю
квадратическую ошибку среднего значения
S
,
которая показывает на сколько может
отклоняться от
"истинного"
результата среднее арифметическое
![]() полученное по результатам наблюдений,
рассчитывают
полученное по результатам наблюдений,
рассчитывают
![]() .
(3.10)
.
(3.10)
Важными в статистике являются показатель точности среднего значения и ошибка среднего квадратического отклонения Ss
![]() ,
(3.11)
,
(3.11)
![]() (3.12)
(3.12)
Выборочные
числовые характеристики являются
надежными количественными оценками
параметров генеральной статистической
совокупности при большом объеме выборок,
а при малом объеме выборки они могут
оказаться грубыми. При ограниченных
объемах выборки особенно важно иметь
представление о точности и надежности
генеральных характеристик. Такое
представление о точности и надежности
оценок дают интервальные оценки,
позволяющие определить величину
максимальной ошибки
![]() ,
которую допускают, приравнивая
,
которую допускают, приравнивая
![]() к
к
![]() .
.
Для
выборок малых объемов,
![]() ,
закон распределения ошибки
,
закон распределения ошибки
![]() описывается
известной функцией распределения
Стьюдента. Используя свойства этого
распределения можно найти доверительный
интервал
описывается
известной функцией распределения
Стьюдента. Используя свойства этого
распределения можно найти доверительный
интервал
![]() (3.13)
(3.13)
где
![]() – средняя квадратическая ошибка среднего
значения;
– средняя квадратическая ошибка среднего
значения;
![]() – критерий
распределения Стьюдента, описывающего
закон распределения ошибки (погрешности
между генеральным и выборочным средним)
приведен в приложении А.
– критерий
распределения Стьюдента, описывающего
закон распределения ошибки (погрешности
между генеральным и выборочным средним)
приведен в приложении А.
Для
выборок объемом,
![]() ,
закон распределения ошибки
,
закон распределения ошибки
![]() доверительный интервал определяют по
формуле
доверительный интервал определяют по
формуле
![]() ,
(3.14)
,
(3.14)
где U – величина для заданного уровня значимости принимается в зависимости от величины p.
|
p |
0,2 |
0,1 |
0,05 |
0,01 |
0,005 |
0,001 |
|
U |
1,28 |
1,64 |
1,966 |
2,58 |
2,81 |
3,29 |
Неравенствами
(3.13), (3.14) задают доверительный интервал,
в котором с вероятностью Р
находится математическое ожидание.
Однако указание только доверительной
вероятности или доверительного интервала
лишено смысла, т. к. утверждение, что
измеренное значение уi
величины
Y
попадает
в интервал
![]() без указания вероятности, с которой это
событие произойдет, не дает никакой
информации.
без указания вероятности, с которой это
событие произойдет, не дает никакой
информации.
При
проведении предварительных (поисковых)
экспериментов доверительную вероятность
принимают
![]() ;
для ответственных исследований, следует
принимать
;
для ответственных исследований, следует
принимать
![]() ;
при изучении слабых влияний, которые
трудно обнаружить или при особо важных
исследованиях, величину доверительной
вероятности принимают в пределах
;
при изучении слабых влияний, которые
трудно обнаружить или при особо важных
исследованиях, величину доверительной
вероятности принимают в пределах
![]() .
.
При выборе доверительного интервала учитывают, что чем точнее нужен результат, тем уже должен быть доверительный интервал.
3.1 Выявление грубых погрешностей
Перед началом обработки результатов экспериментов (измерений) выявляют и исключают из выборки грубые погрешности, которые нарушают нормальное распределение полученной выборки.
Исключение
грубых погрешностей выполняют с
использованием критерия Стьюдента.
Сомнительный результат удаляют из
выборки и по оставшимся элементам
выборки по формулам (3.5 и 3.6) рассчитывают
![]() и
S.
Затем определяют расчетное значение
критерия Стьюдента
и
S.
Затем определяют расчетное значение
критерия Стьюдента
![]() (3.15)
(3.15)
где
![]() – крайний (наибольший или наименьший)
результат выборки;
– крайний (наибольший или наименьший)
результат выборки;
![]() – среднее
арифметическое выборки;
– среднее
арифметическое выборки;
S – среднее квадратическое отклонение выборки.
Далее
расчетное значение
![]() –
критерия сравнивают с критерием Стьюдента
(приложение 1). Если
–
критерия сравнивают с критерием Стьюдента
(приложение 1). Если
![]() при выбранном уровне значимости и числе
степеней свободы
при выбранном уровне значимости и числе
степеней свободы
![]() ,
то данный результат возвращают в выборку
и исследуют другой сомнительный элемент
и т.д.
,
то данный результат возвращают в выборку
и исследуют другой сомнительный элемент
и т.д.
3.2 Полигон и гистограмма частот распределения
Для построения гистограммы частот распределения результаты выборки систематизируют, то есть строят вариационный (ранжированный) ряд, располагая результаты в порядке возрастания. Далее ряд разбивают не некоторое число равной величины интервалов для построения статистического ряда.
Величину интервалов h определяют по формуле
![]() ,
(3.16)
,
(3.16)
где
![]() – максимальный результат выборки;
– максимальный результат выборки;
![]() – минимальный
результат выборки;
– минимальный
результат выборки;
k – число интервалов.
В
качестве нижней границы первого интервала
принимают округленное значение
![]() (важно, чтобы минимальный результат
попал в первый интервал). Если результат
попадает на границу двух интервалов,
то его заносят в интервал с большим
номером. Далее подсчитывают число
наблюдений попавших в каждый интервал
(mi).
Сгруппированные таким образом результаты
называются статистическим рядом.
Количество наблюдений в интервале
называется частотой.
(важно, чтобы минимальный результат
попал в первый интервал). Если результат
попадает на границу двух интервалов,
то его заносят в интервал с большим
номером. Далее подсчитывают число
наблюдений попавших в каждый интервал
(mi).
Сгруппированные таким образом результаты
называются статистическим рядом.
Количество наблюдений в интервале
называется частотой.
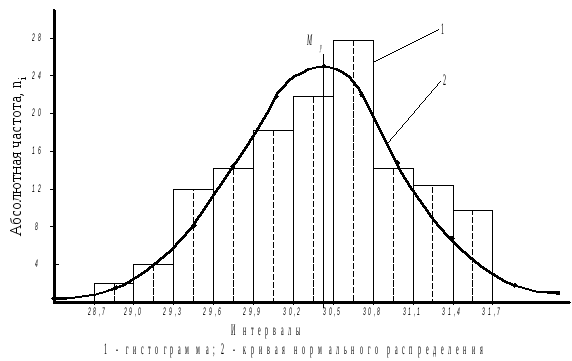
На рисунке 3.2 в качестве примера приведены гистограмма и полигон распределения, являющиеся графическим отображением частот, которые в свою очередь представляют собой оценки плотности вероятности.
|
Р
|
Гистограмма
состоит
из примыкающих друг к другу прямоугольников,
основаниями которых, является длина
интервала h,
а высота соответствует числу элементов
выборки, попавших в данный интервал.
Площадь каждого прямоугольника равна
соответствующей относительной частоте
![]() ,
а полная площадь всей гистограммы равна
единице.
,
а полная площадь всей гистограммы равна
единице.
Полигон
относительных частот
–
ломаная линия, соединяющая точки с
координатами
![]() ;
;
![]() (
(![]() – середина
интервала,
а
– середина
интервала,
а
![]() – соответствующие
им относительные частоты).
– соответствующие
им относительные частоты).
3.3 Построение кривой нормального распределения
При увеличении числа наблюдений и уменьшении величины интервала ломаная кривая полигона относительных частот приближается к некоторой кривой, называемой кривой распределения (кривой плотности вероятности). Она является графиком соотношения между значениями данной случайной величины и их вероятностями. В теории вероятности такое соотношение называется статистическим распределением.
Для случайных величин, имеющих разную природу, статистические распределения могут быть различными (логнормальное, биноминальное и др.). Среди них есть нормальное распределение, в основу которого положено утверждение, что сумма достаточно большого числа произвольно распределенных случайных величин распределена по нормальному закону, и тем точнее, чем больше эта сумма.
Кривую нормального распределения строят на основе уравнения
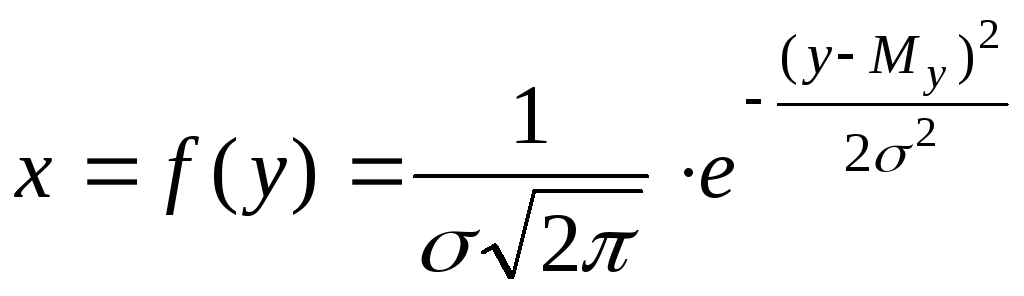 ,
(3.17)
,
(3.17)
Наибольшую
высоту (ординату), соответствующей
среднему значению
![]() измеряемой
величины, в точке
измеряемой
величины, в точке
![]() определяют по формуле
определяют по формуле
![]() ,
(3.18)
,
(3.18)
где h – размер интервала;
N – общее количество наблюдений (объем выборки);
– среднее квадратическое отклонение.
Влево
и вправо от точки
![]() ординаты нормальной кривой будут
симметрично уменьшаться и их вычисляют
по формуле
ординаты нормальной кривой будут
симметрично уменьшаться и их вычисляют
по формуле
![]() ,
(3.19)
,
(3.19)
где k – числовой коэффициент.
Значения коэффициента d
|
d в долях S |
0 |
0,5 |
1,0 |
1,5 |
2,0 |
2,5 |
3,0 |
|
k |
1 |
0,883 |
0,607 |
0,325 |
0,135 |
0,044 |
0,011 |
Каждую ветвь симметричной кривой строят не менее чем по четырем точкам.
По результатам вычислений строят гистограмму и кривую нормального распределения (рисунок 3.3).
|
|
|
Рисунок 3.3 - Гистограмма и кривая нормального распределения |
4 ПРИМЕР ДЛЯ ВЫПОЛНЕНИЯ КУРСОВОЙ РАБОТЫ
4.1 Первичная обработка
В результате продольной распиловки на прирезном станке получены детали, измерение ширины которых имеют размеры, указанные в таблице 4.1.
Таблица 4.1 – Экспериментальные данные (выборка N=100), мм
|
9,42 |
10,64 |
12,07 |
11,80 |
12,76 |
11,26 |
11,55 |
13,16 |
11,58 |
12,42 |
|
12,27 |
10,68 |
12,12 |
11,81 |
10,77 |
11,27 |
11,05 |
13,17 |
11,60 |
12,45 |
|
9,92 |
11,76 |
12,14 |
11,82 |
12,78 |
11,30 |
10,11 |
13,25 |
11,61 |
11,05 |
|
10,30 |
10,88 |
12,15 |
11,84 |
12,80 |
11,32 |
13,62 |
13,26 |
11,65 |
12,56 |
|
10,49 |
11,05 |
12,22 |
11,85 |
12,83 |
11,34 |
10,13 |
13,37 |
11,69 |
12,58 |
|
10,50 |
11,17 |
12,23 |
11,94 |
12,86 |
11,37 |
11,95 |
13,41 |
11,71 |
12,62 |
|
10,53 |
11,17 |
12,25 |
11,97 |
12,93 |
11,38 |
13,87 |
13,42 |
12,23 |
12,64 |
|
11,19 |
11,17 |
12,28 |
12,00 |
12,95 |
11,45 |
12,10 |
13,13 |
11,73 |
12,68 |
|
10,63 |
11,20 |
12,39 |
12,01 |
10,49 |
11,51 |
11,74 |
11,50 |
11,76 |
12,72 |
|
10,24 |
11,23 |
12,40 |
12,07 |
13,00 |
11,51 |
12,26 |
12,13 |
11,76 |
10,73 |
Результаты измерений распологают в порядке возрастания:
9,42; 9,92; 10,11; 10,13; 10,24; 10,30; 10,49; 10,49; 10,50; 10,53; 10,63; 10,64; 10,68; 10,73; 10,77; 10,88; 11,05; 11,05; 11,05; 11,17; 11,17; 11,17; 11,19; 11,20; 11,23; 11,26; 11,27; 11,30; 11,32; 11,34; 11,37; 11,38; 11,45; 11,50; 11,51; 11,51; 11,55; 11,58; 11,60; 11,61; 11,65; 11,69; 11,71; 11,73; 11,74; 11,76; 11,76; 11,76; 11,80; 11,81; 11,82; 11,84; 11,85; 11,94; 11,95; 11,97; 12,00; 12,01; 12,07; 12,07; 12,10; 12,12; 12,13; 12,14; 12,15; 12,22; 12,23; 12,23; 12,25; 12,26; 12,28; 12,39; 12,40; 12,42; 12,45; 12,56; 12,58; 12,62; 12,64; 12,68; 12,72; 12,76; 12,78; 12,80; 12,83; 12,86; 12,93; 12,95; 13,00; 13,13; 13,16; 13,17; 13,25; 13,26; 13,37; 13,41; 13,42; 13,62; 13,87.
Полученный ряд разбивают на несколько равных (обычно нечетное число) интервалов. Количество интервалов k определяют по одной из формул (формулы Стерджеса):
![]() (4.1)
(4.1)
![]() ,
(4.2)
,
(4.2)
где k – число интервалов;
N – число экспериментальных данных в выборке.
![]() ;
;
![]() .
.
Число интервалов принимают k = 9.
Определяют величину интервала h:
![]() (4.3)
(4.3)
где
![]() –
наибольший результат измерения (верхний
предел);
–
наибольший результат измерения (верхний
предел);
![]() – наименьший
результат измерения (нижний предел).
– наименьший
результат измерения (нижний предел).
![]()
Определяют
среднее арифметическое значение выборки
![]() :
:
![]()
![]() .
(4.4)
.
(4.4)
![]()
![]() .
.
Результаты расчета экспериментальных данных приведены в таблице 4.2.
Таблица 4.2 – Результаты расчетов экспериментальных данных
|
Границы интервала |
mi |
yiср |
yiср . mi |
yiср
–
|
(yiср
–
|
(yiср
–
|
|
|
9,42 |
9,91 |
1 |
9,67 |
9,67 |
-2,16 |
4,6687 |
4,6687 |
|
9,92 |
10,41 |
5 |
10,17 |
50,83 |
-1,66 |
2,7599 |
13,7993 |
|
10,42 |
10,90 |
10 |
10,66 |
106,61 |
-1,17 |
1,3615 |
13,6151 |
|
10,91 |
11,40 |
16 |
11,16 |
178,49 |
-0,67 |
0,4521 |
7,2338 |
|
11,41 |
11,89 |
21 |
11,65 |
244,65 |
-0,18 |
0,0317 |
0,6650 |
|
11,90 |
12,39 |
20 |
12,14 |
242,89 |
0,32 |
0,1002 |
2,0034 |
|
12,40 |
12,88 |
14 |
12,64 |
176,94 |
0,81 |
0,6576 |
9,2067 |
|
12,89 |
13,38 |
9 |
13,13 |
118,20 |
1,31 |
1,7040 |
15,3362 |
|
13,39 |
13,87 |
4 |
13,63 |
54,51 |
1,80 |
3,2394 |
12,9575 |
|
|
|
100 |
|
1182,80 |
|
|
79,4858 |
где
![]() –
количество наблюдений в интервале;
–
количество наблюдений в интервале;
![]() – среднее
значение в интервале;
– среднее
значение в интервале;
![]() – среднее
арифметическое значение выборки.
– среднее
арифметическое значение выборки.
Далее определяют среднеквадратичное отклонение S:
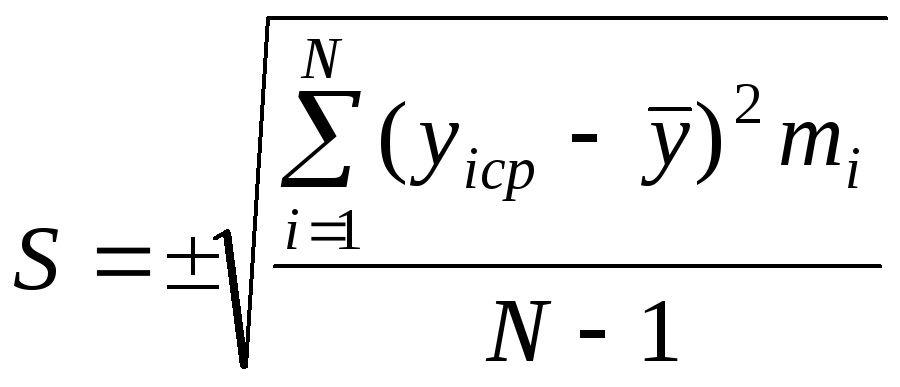 ,
(4.5)
,
(4.5)
![]() .
.
Определяют коэффициент вариации V:
![]() .
(4.6)
.
(4.6)
![]()
Так как, коэффициент вариации менее 33%, то можно выполнять проверку нормальности распределения результатов экспериментальных данных.
Определяют
ошибку среднего квадратического
отклонения ![]()
![]() (4.7)
(4.7)
![]() .
.
Определяют показатель точности среднего значения :
![]() (4.8)
(4.8)
![]() .
.
Так
как
![]() <
1%
, то в данном примере поставленный опыт
выполнен с высокой точностью.
<
1%
, то в данном примере поставленный опыт
выполнен с высокой точностью.
Анализ экспериментальных данных показывает, что некоторые результаты существенно отличаются от большинства измерений, т.е. можно предположить наличие грубых погрешностей.
Исключение
грубых погрешностей выполняют с
использованием критерия Стьюдента
(приложение А). Сомнительный результат
удаляют из выборки и по оставшимся
элементам выборки по формулам (4.4 и 4.5)
рассчитывают
![]() и
S.
Затем определяют расчетное значение t
–
критерия
и
S.
Затем определяют расчетное значение t
–
критерия
![]() ,
(4.9)
,
(4.9)
где
![]() –
подозреваемый на грубую ошибку результат
измерения.
–
подозреваемый на грубую ошибку результат
измерения.
Полученную
расчетом величину сравнивают со значением
критерия Стьюдента при данном значении
числа замеров N,
принятом уровне значимости р
= 0,05
и числе степеней свободы
![]() .
Если
.
Если
![]() ,
то с вероятностью P
= 95%
можно считать результат
,
то с вероятностью P
= 95%
можно считать результат
![]() ошибкой и исключить его из последующей
обработки результатов исследования.
ошибкой и исключить его из последующей
обработки результатов исследования.
![]() ;
;
![]() ;
;
![]() .
.
Исключаем
данные значения, т.к.
![]() и
и
![]() ,
расчеты повторяем до тех пор (статистические
показатели рассчитывают заново, исключая
грубые погрешности), пока не будет
справедливы неравенства:
,
расчеты повторяем до тех пор (статистические
показатели рассчитывают заново, исключая
грубые погрешности), пока не будет
справедливы неравенства:
![]() и
и
![]() .
.
4.2 Определение доверительного интервала
При ограниченных объемах выборки важно представлять значение точности и надежности генеральных характеристик.
Доверительный
интервал – это интервал, в котором с
вероятностью Р
ошибка
лежит в границах
![]() .
.
![]() (4.10)
(4.10)
Oпределяют
истинное значение
![]() ,
которое находится в интервале:
,
которое находится в интервале:
![]()
![]() .
.
По результатам статистической обработки данных строят гистограмму частот распределения. Гистограмма приведена на рисунке 4.1.
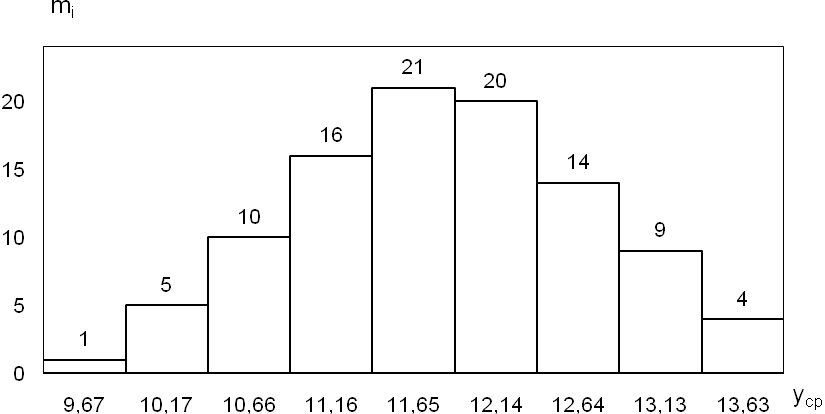
Рисунок 4.1 – Гистограмма частот распределения
Далее строят кривую нормального распределения для сравнения результатов эксперимента с теоретическим распределением.
Наибольшую
высоту (ординату), соответствующую
среднему значению
![]() в точке
в точке
![]() ,
определяют по формуле
,
определяют по формуле
![]() ,
(4.11)
,
(4.11)
где h – величина интервала;
N – общее число наблюдений (объем выборки);
![]() –
среднее
квадратическое отклонение.
–
среднее
квадратическое отклонение.
![]() .
.
Влево
и вправо от точки
![]() ординаты нормальной кривой будут
симметрично уменьшаться. Их вычисляют
по формуле
ординаты нормальной кривой будут
симметрично уменьшаться. Их вычисляют
по формуле
![]() ,
(4.12)
,
(4.12)
где K – числовой коэффициент.
|
Доля S |
0 |
0,5 |
1,0 |
1,5 |
2,0 |
2,5 |
3,0 |
|
K |
1 |
0,883 |
0,607 |
0,325 |
0,135 |
0,044 |
0,011 |
Каждая из ветвей симметрична кривой нормального распределения, должна строится не менее, чем по четырем точкам. Исходные данные для построения кривой нормального распределения представлены в таблице 4.3.
Таблица 4.3 - Данные для построения кривой нормального распределения
|
Доля S |
Пересчётный коэффициент, K |
У |
|
-3,0 |
0,011 |
0,24 |
|
-2,5 |
0,044 |
0,96 |
|
-2,0 |
0,135 |
2,95 |
|
-1,5 |
0,325 |
7,11 |
|
-1,0 |
0,607 |
13,27 |
|
-0,5 |
0,883 |
19,31 |
|
0,0 |
0 |
21,87 |
|
0,5 |
0,883 |
19,31 |
|
1,0 |
0,607 |
13,27 |
|
1,5 |
0,325 |
7,11 |
|
2,0 |
0,135 |
2,95 |
|
2,5 |
0,044 |
0,96 |
|
3,0 |
0,011 |
0,24 |
В
диапазоне
![]() лежит 99,73 % всех данных;
лежит 99,73 % всех данных;
В
диапазоне
![]() – 95,45 %;
– 95,45 %;
В
диапазоне
![]() – 68,27 %.
– 68,27 %.
Кривая нормального распределения приведена на рисунке 4.2.
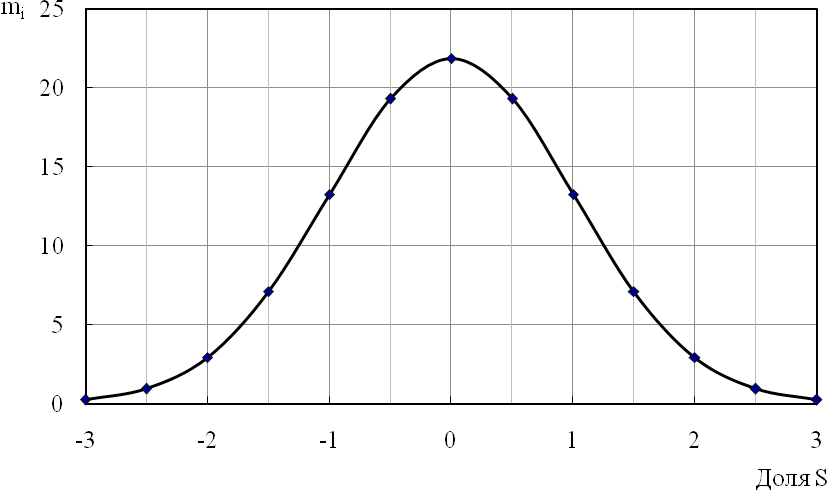
Рисунок 4.2 – Кривая нормального распределения
4.3 Проверка гипотезы о нормальности распределения результатов измерений
Большинство статистических оценок предполагает нормальное распределение результатов опытов и может быть несправедливо в случае другого распределения, поэтому применение этих оценок допустимо при достаточной уверенности, что распределение этих величин подчиняется нормальному закону или близко к нормальному.
Для проверки гипотезы о виде распределения, используют критерий согласия Пирсона (приложение Б). Сущность проверки по критерию согласия состоит в том, что выборка сравнивается с ранее намеченным теоретическим распределением. Вид теоретического распределения выбирают исходя из физического смысла наблюдаемого явления или по характеру кривой эмпирического распределения. С помощью данного критерия можно сравнивать эмпирическое и теоретическое распределения или два различных эмпирических распределения.
![]() (4.13)
(4.13)
где k – количество интервалов, на которые разбиты опытные данные;
![]() – теоретические
вероятности попадания опытных данных
в
i–
ый интервал;
– теоретические
вероятности попадания опытных данных
в
i–
ый интервал;
![]() – теоретические
частоты попадания опытных данных в
i–
ый интервал;
– теоретические
частоты попадания опытных данных в
i–
ый интервал;
mi – эмпирические частоты попадания случайных величин в i– ый интервал.
![]() ,
(4.14)
,
(4.14)
где – Ф0(z) – нормализованная функция Лапласа (приложение В).
![]() ;
(4.15)
;
(4.15)
![]() ,
(4.16)
,
(4.16)
![]() ,
,
![]() – нижняя и верхняя граница интервала.
– нижняя и верхняя граница интервала.
Полученные данные заносят в таблицу 4.3. Необходимо учитывать, что для отрицательного числа функция Лапласа отрицательна.
При уровне значимости 0,05 и числе степеней свободы (f = k – 3) находят табличное значение распределения Пирсона (приложение Б).
Расчетное значение распределения Пирсона получают суммированием значений 12 столбца таблицы 4.3. Суммарное число измерений во всех интервалах mi меньше 100, т.к. часть измерений исключены как грубые погрешности.
![]() .
.
Если
![]() ,
то гипотезу о нормальности распределения
принимают, если
,
то гипотезу о нормальности распределения
принимают, если
![]() ,
то гипотезу отвергают.
,
то гипотезу отвергают.
Таблица 4.3 – Результаты расчетов для проверки гипотезы о нормальности распределения значений результатов эксперимента
|
yiн |
yiв |
mi |
z1 |
z2 |
Ф0(z1) |
Ф0(z2) |
Pi |
PiN |
(mi-PiN)2 |
(mi-PiN)2/(PiN) |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
10,49 |
10,82 |
9 |
-1,91 |
-1,47 |
-0,4719 |
-0,4256 |
0,0463 |
4,2596 |
22,4714 |
5,2755 |
|
10,83 |
11,14 |
4 |
-1,46 |
-1,05 |
-0,4230 |
-0,3531 |
0,0699 |
6,4308 |
5,9088 |
0,9188 |
|
11,15 |
11,47 |
14 |
-1,03 |
-0,61 |
-0,3483 |
-0,2289 |
0,1194 |
10,9848 |
9,0914 |
0,8276 |
|
11,48 |
11,79 |
15 |
-0,59 |
-0,18 |
-0,2224 |
-0,0714 |
0,1510 |
13,8920 |
1,2277 |
0,0884 |
|
11,80 |
12,12 |
14 |
-0,17 |
0,26 |
-0,0675 |
0,1026 |
0,1701 |
15,6492 |
2,7199 |
0,1738 |
|
12,13 |
12,44 |
13 |
0,27 |
0,68 |
0,1064 |
0,2517 |
0,1453 |
13,3676 |
0,1351 |
0,0101 |
|
12,45 |
12,77 |
8 |
0,69 |
1,12 |
0,2599 |
0,3685 |
0,1086 |
9,9912 |
3,9649 |
0,3968 |
|
12,78 |
13,09 |
7 |
1,13 |
1,54 |
0,3664 |
0,4380 |
0,0716 |
6,5872 |
0,1704 |
0,0259 |
|
13,10 |
13,42 |
8 |
1,56 |
1,98 |
0,4344 |
0,4760 |
0,0416 |
3,8272 |
17,4123 |
4,5496 |
|
- |
- |
92 |
- |
- |
- |
- |
- |
- |
- |
12,2665 |
![]() .
.
В
данном случае
![]() – значит, гипотезу о нормальности
распределения принимают.
– значит, гипотезу о нормальности
распределения принимают.
5 РАСЧЕТЫ ПО ПЛАНИРОВАНИЮ ПОЛНОГО ФАКТОРНОГО ЭКСПЕРИМЕНТА
5.1 Расчет реализованного плана полного факторного эксперимента (ПФП)
Расчет (ПФП) заключается в определении коэффициентов уравнения регрессии, проверке значимости этих коэффициентов и установлении адекватности модели (полученного уравнения) (адекватность – соответствие принятой математической модели процесса экспериментальным данным). Уравнение адекватно описывает результаты опытов, если отличие квадратичных отклонений значений выходных параметров (рассчитанных по уравнению регрессии) от экспериментальных данных обусловлены только погрешностью воспроизводимости (то есть от точности воспроизведения результатов опыта при его повторении в одинаковых условиях).
Устанавливают (в соответствии с вариантом задания) переменные и постоянные факторы, оказывающие влияние на процесс пиления и определяют пределы их измерения или величину фиксированного значения.
Для данного примера переменные факторы:
– скорость резания ν = 40..80 м/с;
– толщина распиливаемого материала a = 25..100 мм.
Постоянные факторы:
– порода древесины – ель;
– диаметр пилы d = 400 мм;
– толщина пилы S = 2,2 мм;
– уширение на сторону S0 = 0,6 мм;
– подача на зуб Sz = 0,35 мм;
– число зубьев пилы Z = 48 шт.;
– длительность работы пилы без переточки tраб = 2 часа;
– влажность древесины W = 50 %.
Для оценки воспризводимости опытов составляют таблицу 5.1.
Таблица 5.1 – Значения опытных данных
|
Номер серии опытов |
Переменные факторы |
Выходная величина |
Построчная дисперсия |
||||||
|
v |
a |
y1 |
y2 |
y3 |
y4 |
y5 |
|
Sj2 |
|
|
1 |
–1 |
–1 |
5,2 |
5,6 |
5,8 |
5,8 |
5,3 |
5,54 |
0,312 |
|
2 |
+1 |
–1 |
14,8 |
14,8 |
16,0 |
15,5 |
15,7 |
15,36 |
1,172 |
|
3 |
–1 |
+1 |
11,8 |
10,7 |
11,3 |
11,1 |
11,4 |
11,26 |
0,652 |
|
4 |
+1 |
+1 |
29,3 |
30,2 |
30,8 |
30,5 |
30,8 |
30,32 |
1,548 |
|
|
|
|
|
|
|
|
SЕ = |
Σ Sj2 = |
3,384 |
Определяют
среднее арифметическое значение
![]() для
каждой серии повторных опытов
для
каждой серии повторных опытов
![]() ,
(5.1)
,
(5.1)
где n – число повторных опытов (n = 5).
Построчные дисперсии серии опытов рассчитывают
![]() ,
(5.2)
,
(5.2)
где
![]() – значение выходной величины в i
–
ом дублированном опыте j
–
ой серии;
– значение выходной величины в i
–
ом дублированном опыте j
–
ой серии;
![]() – среднее
арифметическое повторных опытов.
– среднее
арифметическое повторных опытов.
S12 = (5,2 – 5,54)2 + (5,6 – 5,54)2 + (5,8 – 5,54)2 + (5,8 – 5,54)2 +
+ (5,3 – 5,54)2 = 0,312.
Аналогично рассчитывают остальные значения, а результаты заносят в таблицу 5.1.
Следующим этапом оценивают воспроизводимость экспериментальных данных
 (5.3)
(5.3)
где S2jmax – максимальное значение дисперсии серий опытов (из таблицы 5.1);
N – число серий опытов.
![]() .
.
Если
![]() <
<
![]() ,
то опыты воспроизводимы (статистически
однородны), если
,
то опыты воспроизводимы (статистически
однородны), если
![]() – необходимо принять при проведении
исследования более точные методы и
средства измерения.
– необходимо принять при проведении
исследования более точные методы и
средства измерения.
Табличное значение критерия Кохрана (приложение Д) для данного примера при числе степеней свободы f = n – 1= = 5 – 1 = 4 и количестве серий опытов N = 4:
![]() .
.
Так как значение критерия, рассчитанное по опытным данным, не превышает критерия Кохрана, взятого из таблицы, то можно сделать вывод о достаточно хорошей воспроизводимости опытов.
Если бы при расчетах оказалось, что Gрасч > Gтабл, то опыты с максимальной дисперсией следовало бы исключить из рассмотрения, а в условиях реальных экспериментов их необходимо было бы повторить для уточнения причины отклонений.
5.2 Расчет коэффициентов уравнения регрессии
Поскольку установлено, что опыты в точках плана воспроизводимы (ряд построчных дисперсий однороден), рассчитывают коэффициенты уравнения регрессии.
Математическая модель процесса пиления соответствует уравнению регрессии вида:
![]() (5.4)
(5.4)
Для нахождения коэффициентов уравнения регрессии заполняют таблицу 5.2 с учетом таблицы 5.1.
Таблица 5.2 – Исходные данные для расчета коэффициентов уравнения регрессии
|
Номер серии опытов |
|
|
|
|
|
1 |
-5,54 |
-5,54 |
5,54 |
5,54 |
|
2 |
15,36 |
-15,36 |
-15,36 |
15,36 |
|
3 |
-11,26 |
11,26 |
-11,26 |
11,26 |
|
4 |
30,32 |
30,32 |
30,32 |
30,32 |
|
Σ |
28,88 |
20,68 |
9,24 |
62,48 |
Рассчитывают коэффициенты регрессии
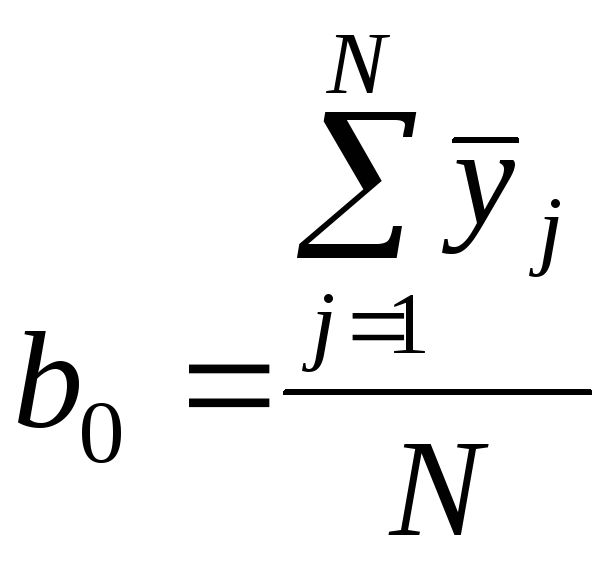 ,
(5.5)
,
(5.5)
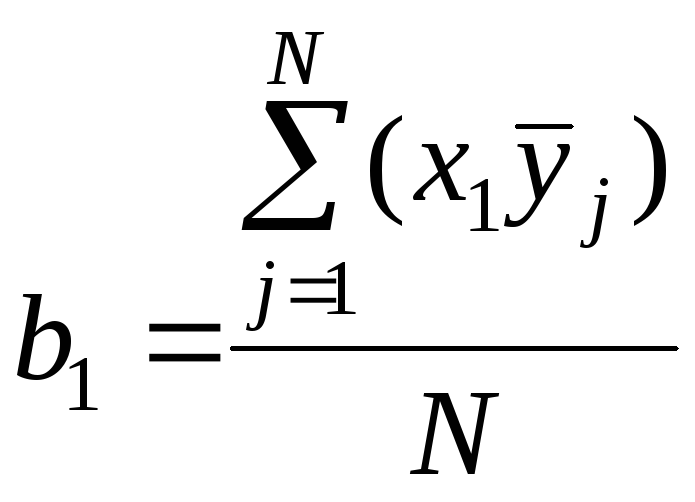 (5.6)
(5.6)
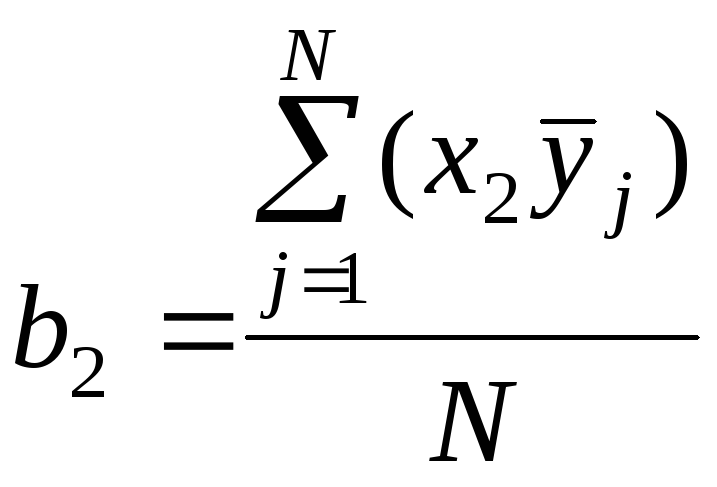 (5.7)
(5.7)
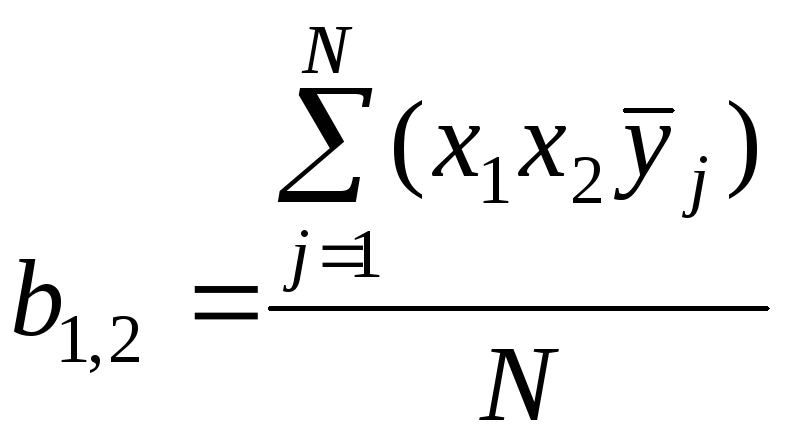 .
(5.8)
.
(5.8)
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
5.3 Определение значимости коэффициентов регрессии
Уравнение регрессии с рассчитанными коэффициентами имеет вид:
![]() .
.
Дисперсию воспроизводимости рассчитывают по формуле
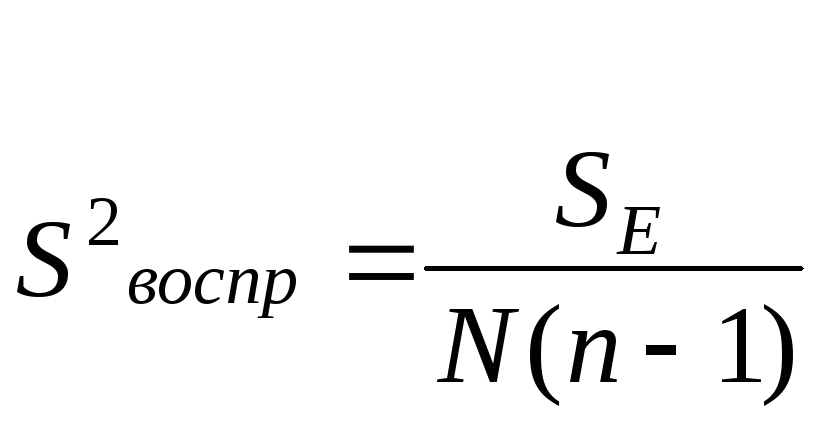 ,
(5.9)
,
(5.9)
![]() .
.
Значимость коэффициентов дисперсии определяют по формуле
![]() (5.10)
(5.10)
где N – число серий опытов;
![]() – дисперсия
воспроизводимости опытов.
– дисперсия
воспроизводимости опытов.
![]()
![]() .
.
В планах ПФП дисперсии коэффициентов при линейных членах и членах, характеризующих взаимодействие различных порядков, равны, что упрощает оценку значимости коэффициентов. Коэффициенты считают значимыми, если выполняется условие:
![]() ,
,
![]() –
коэффициент
Стьюдента,
–
коэффициент
Стьюдента,
при p = 0,05 и при f = N (n – 1) = 4· (5 – 1) = 16;
![]() ,
тогда
,
тогда
![]() .
.
Все коэффициенты в уравнении регрессии значимы, так как превышают по абсолютной величине значение 0,59, и остаются для проверки адекватности модели.
Таким образом, уравнение регрессии с учетом значимых коэффициентов:
![]() .
.
5.4 Проверка уравнения на адекватность
Проверку на адекватность проводят по критерию Фишера, расчетное значение которого находят:
 .
(5.11)
.
(5.11)
Таблица 5.2 – Проверка на адекватность при помощи критерия Фишера
|
Номер серии опытов |
b0 |
b1x1 |
b2x2 |
b1,2x1x2 |
|
|
|
|
1 |
15,62 |
-7,22 |
-5,17 |
2,31 |
5,54 |
5,54 |
0 |
|
2 |
15,62 |
7,22 |
-5,17 |
-2,31 |
15,36 |
15,36 |
0 |
|
3 |
15,62 |
-7,22 |
5,17 |
-2,31 |
11,26 |
11,26 |
0 |
|
4 |
15,62 |
7,22 |
5,17 |
2,31 |
30,32 |
30,32 |
0 |
|
Σ |
- |
- |
- |
- |
- |
- |
0 |
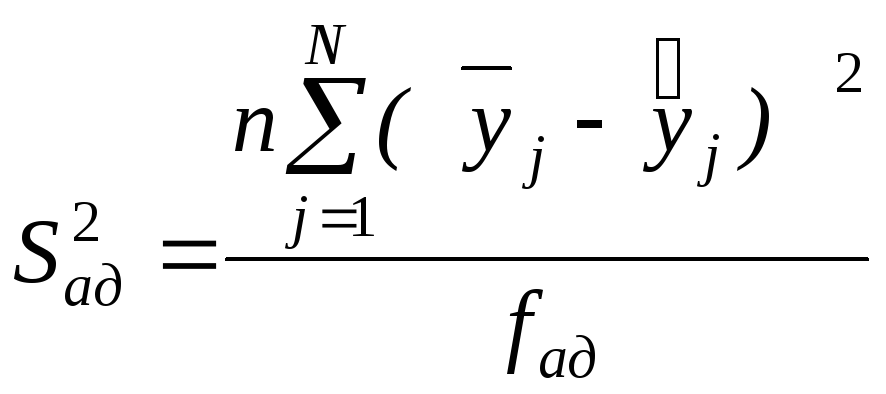 ,
(5.12)
,
(5.12)
где
![]() – дисперсия адекватности;
– дисперсия адекватности;
fад – число степеней свободы , равно N – m;
N – число серий опытов;
m – число значимых коэффициентов уравнения регрессии с учетом свободного члена;
![]() – средние
значения выходной величины из таблицы
5.1;
– средние
значения выходной величины из таблицы
5.1;
![]() –
расчетные
значения выходной величины (определяют
построчным суммированием b0+
b1x1+
b2x2+
b1,2x1x2
с
учетом знаков).
–
расчетные
значения выходной величины (определяют
построчным суммированием b0+
b1x1+
b2x2+
b1,2x1x2
с
учетом знаков).
![]() ;
;
![]() .
.
Таким образом, уравнение заведомо адекватно, так как S2ад. = 0.
Расчетное значение сравнивают с критерием Фишера, принимаемым по таблице (приложение Д).
При f1= n – 1=5 – 1= 4 и f2=N(n – 1)=4(5 –1)=16, Fтабл = 3,0.
Так как, расчетное значение критерия (= 0) не превосходит табличное значение критерия Фишера (= 3,3), то полученное уравнение адекватно.
5.5 Приведение уравнения регрессии к натуральным значениям
Нормализованные и натуральные значения факторов связаны следующим соотношением
![]() ,
(5.13)
,
(5.13)
где xi – нормализованное значение переменного фактора;
![]() ,
,
![]() – натуральные значения факторов;
– натуральные значения факторов;
Δi – интервал варьирования.
![]() ,
(5.14)
,
(5.14)
![]() ,
(5.15)
,
(5.15)
где Xi max, Xi min – значения факторов на верхнем и нижнем уровнях.
Фактор x1: v = 40..80 м/с:
![]() м/с;
м/с;
![]() м/с;
м/с;
![]() .
.
Фактор x2: a = 25..100 мм:
![]() мм;
мм;
![]() мм;
мм;
![]() .
.
![]() ;
;
![]() .
.
5.6 Построение поверхности отклика
Поверхность отклика строят с учетом двух факторов, совмещая расчетную и рабочую матрицы (таблица 5.3):
фактор x1 – v – скорость резания;
фактор x2 – a – толщина распиливаемого материала.
Таблица 5.3 – Исходные данные для построения поверхности отклика
|
Номер серии опытов |
v |
a |
Оценочный показатель Pi, кВт |
||
|
|
м/с |
|
мм |
||
|
1 |
-1 |
40 |
-1 |
25 |
5,54 |
|
2 |
+1 |
80 |
-1 |
25 |
15,36 |
|
3 |
-1 |
40 |
+1 |
100 |
11,26 |
|
4 |
+1 |
80 |
+1 |
100 |
30,32 |
![]() кВт;
кВт;
![]() кВт;
кВт;
![]() кВт;
кВт;
![]() кВт.
кВт.
Поверхность отклика представлена на рисунке 5.1.

Рисунок 5.1 – Поверхность отклика
ПРИЛОЖЕНИЕ А
Квантили распределения Стьюдента t(p,f)
(p – уровень значимости, f – число степеней свободы)
|
Число степеней свободы, f |
Уровни значимости, р |
||||||
|
|
0,20 |
0,10 |
0,05 |
0,02 |
0,01 |
0,005 |
0,001 |
|
1 |
3,08 |
6,31 |
12,71 |
31,82 |
63,66 |
127,32 |
636,32 |
|
2 |
1,89 |
2,92 |
4,30 |
6,97 |
9,93 |
14,09 |
31,60 |
|
3 |
1,64 |
2,35 |
3,18 |
4,54 |
5,84 |
7,45 |
12,94 |
|
4 |
1,53 |
2,13 |
2,78 |
3,75 |
4,60 |
5,60 |
8,61 |
|
5 |
1,48 |
2,02 |
2,57 |
3,37 |
4,03 |
4,77 |
6,86 |
|
6 |
1,44 |
1,94 |
2,45 |
3,14 |
3,71 |
4,32 |
5,96 |
|
7 |
1,42 |
1,90 |
2,37 |
3,00 |
3,50 |
4,03 |
5,41 |
|
8 |
1,40 |
1,86 |
2,31 |
2,90 |
3,36 |
3,83 |
5,04 |
|
9 |
1,38 |
1,83 |
2,26 |
2,82 |
3,25 |
3,69 |
4,78 |
|
10 |
1,37 |
1,81 |
2,23 |
2,76 |
3,17 |
3,58 |
4,59 |
|
11 |
1,36 |
1,80 |
2,20 |
2,72 |
3,11 |
3,50 |
4,44 |
|
12 |
1,36 |
1,78 |
2,18 |
2,68 |
3,06 |
3,43 |
4,32 |
|
13 |
1,35 |
1,77 |
2,16 |
2,65 |
3,01 |
3,37 |
4,22 |
|
14 |
1,34 |
1,76 |
2,15 |
2,62 |
2,98 |
3,33 |
4,14 |
|
15 |
1,34 |
1,75 |
2,13 |
2,60 |
2,95 |
3,29 |
4,07 |
|
16 |
1,34 |
1,75 |
2,12 |
2,58 |
2,92 |
3,25 |
4,02 |
|
17 |
1,33 |
1,74 |
2,11 |
2,57 |
2,90 |
3,22 |
3,97 |
|
18 |
1,33 |
1,73 |
2,10 |
2,55 |
2,88 |
3,20 |
3,92 |
|
19 |
1,33 |
1,73 |
2,09 |
2,54 |
2,86 |
3,17 |
3,88 |
|
20 |
1,33 |
1,73 |
2,09 |
2,53 |
2,85 |
3,15 |
3,85 |
|
22 |
1,32 |
1,72 |
2,07 |
2,51 |
2,82 |
3,12 |
3,79 |
|
24 |
1,32 |
1,71 |
2,06 |
2,49 |
2,80 |
3,09 |
3,75 |
|
26 |
1,32 |
1,71 |
2,06 |
2,48 |
2,78 |
3,07 |
3,71 |
|
28 |
1,31 |
1,70 |
2,05 |
2,47 |
2,76 |
3,05 |
3,67 |
|
30 |
1,31 |
1,70 |
2,04 |
2,46 |
2,75 |
3,03 |
3,65 |
|
40 |
1,30 |
1,68 |
2,02 |
2,42 |
2,70 |
2,97 |
3,55 |
|
60 |
1,30 |
1,67 |
2,00 |
2,39 |
2,66 |
2,91 |
3,46 |
|
120 |
1,29 |
1,66 |
1,98 |
2,36 |
2,62 |
2,86 |
3,37 |
|
∞ |
1,28 |
1,64 |
1,96 |
2,33 |
2,58 |
2,81 |
3,29 |
ПРИЛОЖЕНИЕ Б
Значение f2(t) – распределение Пирсона
(р – уровень значимости, f – число степеней свободы)
|
p/f |
0,50 |
0,30 |
0,20 |
0,10 |
0,05 |
0,02 |
0,01 |
|
1 |
0,455 |
1,074 |
1,672 |
2,706 |
3,841 |
5,412 |
6,635 |
|
2 |
1,386 |
2,408 |
3,219 |
4,605 |
5,991 |
7,824 |
9,210 |
|
3 |
2,366 |
3,665 |
4,642 |
6,251 |
7,815 |
9,937 |
11,345 |
|
4 |
3,357 |
4,878 |
5,980 |
7,779 |
9,488 |
11,668 |
13,277 |
|
5 |
4,351 |
6,064 |
7,289 |
9,236 |
11,070 |
13,388 |
15,068 |
|
6 |
5,348 |
7,231 |
8,558 |
10,645 |
12,592 |
15,033 |
16,812 |
|
7 |
6,346 |
8,383 |
9,803 |
12,017 |
14,067 |
16,622 |
18,475 |
|
8 |
7,344 |
9,524 |
11,030 |
13,362 |
15,507 |
18,168 |
20,090 |
|
9 |
8,343 |
10,656 |
12,242 |
14,684 |
16,919 |
19,679 |
21,666 |
|
10 |
9,342 |
11,781 |
13,442 |
15,987 |
18,307 |
21,161 |
23,209 |
|
11 |
10,341 |
12,899 |
14,631 |
17,275 |
19,675 |
22,618 |
24,725 |
|
12 |
11,340 |
14,011 |
15,812 |
18,549 |
21,026 |
24,054 |
26,217 |
|
13 |
12,340 |
15,119 |
16,985 |
19,812 |
22,362 |
25,472 |
27,688 |
|
14 |
13,339 |
16,222 |
18,151 |
21,064 |
23,685 |
26,873 |
29,141 |
|
15 |
14,339 |
17,322 |
19,311 |
22,307 |
24,996 |
28,259 |
30,578 |
|
16 |
15,338 |
18,418 |
20,465 |
23,542 |
26,296 |
29,633 |
32,000 |
|
17 |
16,338 |
19,511 |
21,615 |
24,769 |
27,587 |
30,995 |
33,409 |
|
18 |
17,338 |
20,601 |
22,760 |
25,989 |
28,869 |
32,346 |
34,805 |
|
19 |
18,388 |
21,689 |
23,900 |
27,204 |
30,114 |
33,687 |
36,191 |
|
20 |
19,337 |
22,775 |
25,038 |
28,412 |
31,410 |
35,020 |
37,566 |
|
21 |
20,337 |
23,858 |
26,171 |
29,615 |
32,671 |
36,343 |
38,932 |
|
22 |
21,337 |
24,939 |
27,301 |
30,813 |
33,924 |
37,659 |
40,289 |
|
23 |
22,337 |
26,018 |
28,429 |
32,007 |
35,172 |
38,968 |
41,638 |
|
24 |
23,337 |
27,096 |
29,553 |
33,196 |
36,415 |
40,270 |
42,980 |
|
25 |
24,337 |
28,172 |
30,675 |
34,382 |
37,652 |
41,566 |
44,314 |
|
26 |
25,336 |
29,246 |
31,795 |
35,563 |
38,885 |
42,856 |
45,642 |
|
27 |
26,336 |
30,319 |
32,912 |
36,741 |
40,113 |
44,140 |
46,963 |
|
28 |
27,336 |
31,391 |
34,027 |
37,916 |
41,337 |
45,419 |
48,278 |
|
29 |
28,336 |
32,461 |
35,139 |
39,087 |
42,557 |
46,693 |
49,588 |
|
30 |
29,336 |
33,530 |
36,250 |
40,256 |
43,773 |
47,962 |
50,892 |
ПРИЛОЖЕНИЕ В
Значения
функции Лапласа Ф(z)
=
![]()
|
z |
Ф(z) |
z |
Ф(z) |
z |
Ф(z) |
|
0,00 |
0,0000 |
0,29 |
0,1141 |
0,58 |
0,2190 |
|
0,01 |
0,0040 |
0,30 |
0,1179 |
0,59 |
0,2224 |
|
0,02 |
0,0080 |
0,31 |
0,1217 |
0,60 |
0,2257 |
|
0,03 |
0,0120 |
0,32 |
0,1255 |
0,61 |
0,2291 |
|
0,04 |
0,0160 |
0,33 |
0,1293 |
0,62 |
0,2324 |
|
0,05 |
0,0199 |
0,34 |
0,1331 |
0,63 |
0,2357 |
|
0,06 |
0,0239 |
0,35 |
0,1368 |
0,64 |
0,2389 |
|
0,07 |
0,0279 |
0,36 |
0,1406 |
0,65 |
0,2422 |
|
0,08 |
0,0319 |
0,37 |
0,1443 |
0,66 |
0,2454 |
|
0,09 |
0,0359 |
0,38 |
0,1480 |
0,67 |
0,2486 |
|
0,10 |
0,0398 |
0,39 |
0,1517 |
0,68 |
0,2517 |
|
0,11 |
0,0438 |
0,40 |
0,1554 |
0,69 |
0,2549 |
|
0,12 |
0,0478 |
0,41 |
0,1591 |
0,70 |
0,2580 |
|
0,13 |
0,0517 |
0,42 |
0,1628 |
0,71 |
0,2611 |
|
0,14 |
0,0557 |
0,43 |
0,1664 |
0,72 |
0,2642 |
|
0,15 |
0,0596 |
0,44 |
0,1700 |
0,73 |
0,2673 |
|
0,16 |
0,0636 |
0,45 |
0,1736 |
0,74 |
0,2703 |
|
0,17 |
0,0675 |
0,46 |
0,1772 |
0,75 |
0,2734 |
|
0,18 |
0,0714 |
0,47 |
0,1808 |
0,76 |
0,2764 |
|
0,19 |
0,0753 |
0,48 |
0,1844 |
0,77 |
0,2794 |
|
0,20 |
0,0793 |
0,49 |
0,1879 |
0,78 |
0,2823 |
|
0,21 |
0,0832 |
0,50 |
0,1915 |
0,79 |
0,2852 |
|
0,22 |
0,0871 |
0,51 |
0,1950 |
0,80 |
0,2881 |
|
0,23 |
0,0910 |
0,52 |
0,1985 |
0,81 |
0,2910 |
|
0,24 |
0,0948 |
0,53 |
0,2019 |
0,82 |
0,2939 |
|
0,25 |
0,0987 |
0,54 |
0,2054 |
0,83 |
0,2967 |
|
0,26 |
0,1026 |
0,55 |
0,2088 |
0,84 |
0,2995 |
|
0,27 |
0,1064 |
0,56 |
0,2123 |
0,85 |
0,3023 |
|
0,28 |
0,1103 |
0,57 |
0,2157 |
0,86 |
0,3051 |
ПРИЛОЖЕНИЕ В (продолжение)
|
z |
Ф(z) |
z |
Ф(z) |
z |
Ф(z) |
|
0,87 |
0,3078 |
1,22 |
0,3883 |
1,57 |
0,4418 |
|
0,88 |
0,3106 |
1,23 |
0,3907 |
1,58 |
0,4429 |
|
0,89 |
0,3133 |
1,24 |
0,3925 |
1,59 |
0,4441 |
|
0,90 |
0,3159 |
1,25 |
0,3944 |
1,60 |
0,4452 |
|
0,91 |
0,3186 |
1,26 |
0,3962 |
1,61 |
0,4463 |
|
0,92 |
0,3212 |
1,27 |
0,3980 |
1,62 |
0,4474 |
|
0,93 |
0,3238 |
1,28 |
0,3997 |
1,63 |
0,4484 |
|
0,94 |
0,3264 |
1,29 |
0,4015 |
1,64 |
0,4495 |
|
0,95 |
0,3289 |
1,30 |
0,4032 |
1,65 |
0,4505 |
|
0,96 |
0,3315 |
1,31 |
0,4049 |
1,66 |
0,4515 |
|
0,97 |
0,3340 |
1,32 |
0,4066 |
1,67 |
0,4525 |
|
0,98 |
0,3365 |
1,33 |
0,4082 |
1,68 |
0,4535 |
|
0,99 |
0,3389 |
1,34 |
0,4099 |
1,69 |
0,4545 |
|
1,00 |
0,3413 |
1,35 |
0,4115 |
1,70 |
0,4554 |
|
1,01 |
0,3438 |
1,36 |
0,4131 |
1,71 |
0,4564 |
|
1,02 |
0,3461 |
1,37 |
0,4147 |
1,72 |
0,4573 |
|
1,03 |
0,3485 |
1,38 |
0,4162 |
1,73 |
0,4582 |
|
1,04 |
0,3508 |
1,39 |
0,4177 |
1,74 |
0,4591 |
|
1,05 |
0,3531 |
1,40 |
0,4192 |
1,75 |
0,4599 |
|
1,06 |
0,3554 |
1,41 |
0,4207 |
1,76 |
0,4608 |
|
1,07 |
0,3577 |
1,42 |
0,4222 |
1,77 |
0,4616 |
|
1,08 |
0,3599 |
1,43 |
0,4236 |
1,78 |
0,4625 |
|
1,09 |
0,3621 |
1,44 |
0,4251 |
1,79 |
0,4633 |
|
1,10 |
0,3643 |
1,45 |
0,4265 |
1,80 |
0,4641 |
|
1,11 |
0,3665 |
1,46 |
0,4279 |
1,81 |
0,4649 |
|
1,12 |
0,3686 |
1,47 |
0,4292 |
1,82 |
0,4546 |
|
1,13 |
0,3708 |
1,48 |
0,4306 |
1,83 |
0,4664 |
|
1,14 |
0,3729 |
1,49 |
0,4319 |
1,84 |
0,4671 |
|
1,15 |
0,3749 |
1,50 |
0,4332 |
1,85 |
0,4678 |
|
1,16 |
0,3770 |
1,51 |
0,4345 |
1,86 |
0,4686 |
|
1,17 |
0,3790 |
1,52 |
0,4357 |
1,87 |
0,4693 |
|
1,18 |
0,3810 |
1,53 |
0,4370 |
1,88 |
0,4699 |
|
1,19 |
0,3830 |
1,54 |
0,4382 |
1,89 |
0,4706 |
|
1,20 |
0,3849 |
1,55 |
0,4394 |
1,90 |
0,4713 |
|
1,21 |
0,3869 |
1,56 |
0,4406 |
1,91 |
0,4719 |
ПРИЛОЖЕНИЕ В (продолжение)
|
z |
Ф(z) |
z |
Ф(z) |
z |
Ф(z) |
|
1,92 |
0,4726 |
2,28 |
0,4887 |
2,72 |
0,4967 |
|
1,93 |
0,4732 |
2,30 |
0,4893 |
2,74 |
0,4969 |
|
1,94 |
0,4738 |
2,32 |
0,4898 |
2,76 |
0,4971 |
|
1,95 |
0,4744 |
2,34 |
0,4904 |
2,78 |
0,4973 |
|
1,96 |
0,4750 |
2,36 |
0,4909 |
2,80 |
0,4974 |
|
1,97 |
0,4756 |
2,38 |
0,4913 |
2,82 |
0,4976 |
|
1,98 |
0,4761 |
2,40 |
0,4918 |
2,84 |
0,4977 |
|
1,99 |
0,4767 |
2,42 |
0,4922 |
2,86 |
0,4979 |
|
2,00 |
0,4772 |
2,44 |
0,4927 |
2,88 |
0,4980 |
|
2,02 |
0,4783 |
2,46 |
0,4931 |
2,90 |
0,4981 |
|
2,04 |
0,4793 |
2,48 |
0,4934 |
2,92 |
0,4982 |
|
2,06 |
0,4803 |
2,50 |
0,4938 |
2,94 |
0,4984 |
|
2,08 |
0,4812 |
2,52 |
0,4941 |
2,96 |
0,49846 |
|
2,10 |
0,4821 |
2,54 |
0,4945 |
2,98 |
0,49856 |
|
2,12 |
0,4830 |
2,56 |
0,4948 |
3,00 |
0,49865 |
|
2,14 |
0,4838 |
2,58 |
0,4951 |
3,20 |
0,49931 |
|
2,16 |
0,4846 |
2,60 |
0,4953 |
3,40 |
0,49966 |
|
2,18 |
0,4854 |
2,62 |
0,4956 |
3,60 |
0,49984 |
|
2,20 |
0,4861 |
2,64 |
0,4959 |
3,80 |
0,499928 |
|
2,22 |
0,4868 |
2,66 |
0,4961 |
4,00 |
0,499968 |
|
2,24 |
0,4875 |
2,68 |
0,4963 |
5,00 |
0,499997 |
|
2,26 |
0,4881 |
2,70 |
0,4965 |
|
|
ПРИЛОЖЕНИЕ Г
Квантили распределения Фишера для уровня значимости р = 0,05
|
f2 |
f1 |
||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
12 |
24 |
00 |
|
|
1 |
164,4 |
199,5 |
215,7 |
224,6 |
230,2 |
234,0 |
244,9 |
249 |
254,3 |
|
2 |
18,5 |
19,2 |
19,2 |
19,3 |
19,3 |
19,3 |
19,4 |
19,5 |
19,5 |
|
3 |
10,1 |
9,6 |
9,3 |
9,1 |
9,0 |
8,9 |
8,7 |
8,6 |
8,5 |
|
4 |
7,7 |
6,9 |
6,6 |
6,4 |
6,3 |
6,2 |
5,9 |
5,8 |
5,6 |
|
5 |
6,6 |
5,8 |
5,4 |
5,2 |
5,1 |
5,0 |
4,7 |
4,5 |
4,4 |
|
6 |
6,0 |
5,1 |
4,8 |
4,5 |
4,4 |
4,3 |
4,0 |
3,8 |
3,7 |
|
7 |
5,6 |
4,7 |
4,4 |
4,1 |
4,0 |
3,9 |
3,6 |
3,4 |
3,2 |
|
8 |
5,3 |
4,5 |
4,1 |
3,8 |
3,7 |
3,6 |
3,3 |
3,1 |
2,9 |
|
9 |
5,1 |
4,3 |
3,9 |
3,6 |
3,5 |
3,4 |
3,1 |
2,9 |
2,7 |
|
10 |
5,0 |
4,1 |
3,7 |
3,5 |
3,3 |
3,2 |
2,9 |
2,7 |
2,5 |
|
11 |
4,8 |
4,0 |
3,6 |
3,4 |
3,2 |
3,1 |
2,8 |
2,6 |
2,4 |
|
12 |
4,8 |
3,9 |
3,5 |
3,3 |
3,1 |
3,0 |
2,7 |
2,5 |
2,3 |
|
13 |
4,7 |
3,8 |
3,4 |
3,2 |
3,0 |
2,9 |
2,6 |
2,4 |
2,2 |
|
14 |
4,6 |
3,7 |
3,3 |
3,1 |
3,0 |
2,9 |
2,5 |
2,3 |
2,1 |
|
15 |
4,5 |
3,7 |
3,3 |
3,1 |
2,9 |
2,8 |
2,5 |
2,3 |
2,1 |
|
16 |
4,5 |
3,6 |
3,2 |
3,0 |
2,9 |
2,7 |
2,4 |
2,2 |
2,0 |
|
17 |
4,5 |
3,6 |
3,2 |
3,0 |
2,8 |
2,7 |
2,4 |
2,2 |
2,0 |
|
18 |
4,4 |
3,6 |
3,2 |
2,9 |
2,8 |
2,7 |
2,3 |
2,1 |
1,9 |
|
19 |
4,4 |
3,5 |
3,1 |
2,9 |
2,7 |
2,6 |
2,3 |
2,1 |
1,8 |
|
20 |
4,4 |
3,5 |
3,1 |
2,9 |
2,7 |
2,6 |
2,3 |
2,1 |
1,8 |
|
22 |
4,3 |
3,4 |
3,1 |
2,8 |
2,7 |
2,6 |
2,2 |
2,0 |
1,8 |
|
24 |
4,3 |
3,4 |
3,0 |
2,8 |
2,6 |
2,5 |
2,2 |
2,0 |
1,7 |
|
26 |
4,2 |
3,4 |
3,0 |
2,7 |
2,6 |
2,4 |
2,1 |
1,9 |
1,7 |
|
28 |
4,2 |
3,3 |
2,9 |
2,7 |
2,6 |
2,4 |
2,1 |
1,9 |
1,6 |
|
30 |
4,2 |
3,3 |
2,9 |
2,7 |
2,5 |
2,4 |
2,1 |
1,9 |
1,6 |
|
40 |
4,1 |
3,2 |
2,9 |
2,6 |
2,5 |
2,3 |
2,0 |
1,8 |
1,5 |
|
60 |
4,0 |
3,2 |
2,8 |
2,5 |
2,4 |
2,3 |
1,9 |
1,7 |
1,4 |
|
120 |
3,9 |
3,1 |
2,7 |
2,5 |
2,3 |
2,2 |
1,8 |
1,6 |
1,3 |
|
∞ |
3,8 |
3,0 |
2,6 |
2,4 |
2,2 |
2,1 |
1,8 |
1,5 |
1,0 |
ПРИЛОЖЕНИЕ Д
Квантили* распределения Кохрана для уровня значимости р = 0,05
|
N |
f |
||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
8 |
10 |
16 |
36 |
∞ |
|
|
2 |
9985 |
9750 |
9392 |
9057 |
8772 |
8534 |
8159 |
7880 |
7341 |
6602 |
5000 |
|
3 |
9669 |
8709 |
7977 |
7454 |
7071 |
6771 |
6333 |
6025 |
5466 |
4748 |
3333 |
|
4 |
9065 |
7679 |
6841 |
6287 |
5895 |
5598 |
5175 |
4884 |
4366 |
3720 |
2500 |
|
5 |
8412 |
6838 |
5981 |
5441 |
5065 |
4783 |
4387 |
4118 |
3645 |
3066 |
2000 |
|
6 |
7808 |
6161 |
5321 |
4803 |
4447 |
4184 |
3817 |
3568 |
3135 |
2612 |
1667 |
|
7 |
7271 |
5612 |
4800 |
4307 |
3974 |
3726 |
3384 |
3154 |
2756 |
2278 |
1429 |
|
8 |
6798 |
5157 |
4377 |
3910 |
3595 |
3362 |
3043 |
2829 |
2462 |
2022 |
1250 |
|
9 |
6385 |
4775 |
4027 |
3584 |
3286 |
3067 |
2768 |
2568 |
2226 |
1820 |
1111 |
|
10 |
6020 |
4450 |
3733 |
3311 |
3029 |
2823 |
2541 |
2353 |
2032 |
1655 |
1000 |
|
12 |
5410 |
3924 |
3264 |
2880 |
2624 |
2439 |
2187 |
2020 |
1737 |
1403 |
0833 |
|
15 |
4709 |
3346 |
2758 |
2419 |
2195 |
2034 |
1815 |
1671 |
1429 |
1144 |
0667 |
|
20 |
3894 |
2705 |
2205 |
1921 |
1735 |
1602 |
1422 |
1303 |
1108 |
0879 |
0500 |
|
24 |
3434 |
2354 |
1907 |
1656 |
1493 |
1374 |
1216 |
1113 |
0942 |
0743 |
0417 |
|
30 |
2929 |
1980 |
1593 |
1377 |
1237 |
1137 |
1001 |
0921 |
0771 |
0604 |
0333 |
|
40 |
2370 |
1576 |
1259 |
1082 |
0968 |
0887 |
0780 |
0713 |
0595 |
0462 |
0250 |
|
60 |
1737 |
1131 |
0895 |
0765 |
0682 |
0623 |
0552 |
0497 |
0411 |
0316 |
0167 |
|
120 |
0998 |
0632 |
0495 |
0419 |
0371 |
0337 |
0292 |
0266 |
0218 |
0165 |
0083 |
|
∞ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
* Все квантили меньше единицы, поэтому в таблице приведены лишь десятичные знаки, следующие после запятой, перед которой при пользовании таблицей нужно ставить ноль целых. Например, при N = 4, f= 4 имеем G = 0,6287.
Кафедра стандартизации, метрологии и сертификации

 исунок
3.2 – Гистограмма и полигон распределения
исунок
3.2 – Гистограмма и полигон распределения