22

ПВНЗ Буковинський університет

Факультет комп’ютерних систем і технологій

кафедра " Комп’ютерних систем і технологій "

КУРСОВА РОБОТА

З ПРЕДМЕТУ

" Моделювання інформаційних процесів"

НА ТЕМУ:

" Реконструкція фазового простору динамічної системи в середовищі Maple "

Виконав:

студент V курсу

групи Км - 501

Кульбашний Р.О.

Керівник : доц.,к.ф-м. наук Сопін М.О.

Чернівці 2011

Зміст

ВСТУП 3

1. Динамічні системи 4

1.1. Поняття динамічної системи 4

1.2. Фазовий портрет динамічної системи. Теорема Такенса 6

2. Реконструкція фазового простору динамічної системи 11

2.1. Алгоритм відновлення простору станів динамічної системи 11

2.2. Реконструкція фазового простору деяких динамічних систем в середовищі Maple 11

ВИСНОВКИ 21

ПЕРЕЛІК ВИКОРИСТАНИХ ДЖЕРЕЛ 22

ВСТУП

Для багатьох дослідників вивчення динаміки почалося і закінчилося другим законом Ньютона F = ma. Якщо задані сили, що діють між частками, а також початкові положення і швидкості часток, то за допомогою достатнього великого комп'ютера можна передбачити рух або розвиток системи для будь-якого скільки завгодно пізнього часу. Проте поява великих потужних комп'ютерів не привела до обіцяної нескінченної передбаченості в динаміці. Було виявлено, що рух деяких простих динамічних систем не завжди можна передбачити на великий інтервал часу. Такі рухи були названі хаотичними, і їх дослідження привабило в динаміку деякі нові математичні ідеї [1,2,3].

В даний час широко проводяться дослідження з моделювання складних динамічних систем. Це пояснюється тим, що динамічна поведінка великого числа систем і технічних пристроїв має динамічно складний характер: нерегулярні та хаотичні явища, біфуркації і т. д. Однак ці процеси можуть бути отримані і за допомогою більш обчислювально-надійних моделей регулярної динаміки. При цьому на систему діють заздалегідь запрограмовані обурення, призводять керовану систему до періодичної орбіти з бажаними властивостями, тобто близько до "хаотичної" поведінки [4].

Тому актуальність вивчення динаміних систем та реконструкції їх фазових просторів є безсумнівною. Метою даної курсової роботи було вивчення поведінки деяких динамічних систем (осцилятор, система Лореца) та реконструкції їх фазового простору. Об’єктом дослідження є динамічна система, а предметом дослідження є фазовий простір.

Задача розв’язувалась в середовищі комп’ютерної алгебри „Maple” з використанням необхідних пакетів.

1. Динамічні системи

1.1. Поняття динамічної системи

Як об'єкт дослідження розглянемо динамічні керовані системи з дискретним часом, які локально можуть бути описані відображенням F::

(1)

де x(t) – n-мірний вектор стану системи, x(t) – r-мірний вектор параметрів системи; t – дискретний час. Мета управління полягає у виконанні заданої програми руху, тобто система повинна моделювати періодичну, можливо нестійку, траєкторію. Лінеарізуем рівняння (1) вздовж цієї траєкторії:

(2)

де – матриця Якобі, яка визнчає властивості стійкості системи за Ляпуновим. – матриця, що визначає лінійний відгук системи на збурення.

Будемо розглядати в рамках проблеми ідентифікації системи завдання реконструкції фазового портрету складної динамічної системи. Апріорі передбачається, що складна система допускає групи симетрій.

Визначимо симетрію систем як лінійне перетворення в просторі станів, при якому нелінійне рівняння динаміки (1) зберігає свою структуру. Більш формально рівняння (1), процес який володіє симетрією і описується групою симетрій G, якщо відображення F комутує по всім груповим операціями:

(3)

або, іншими словами, група G робить функцію інваріантної по першому аргументу. Група G зазвичай є продуктом симетрії фізичного інтервалу, наприклад, симетрія обертання або симетрія зсуву простору фази – . Як правило, всі групи симетрій, що допускаються рівняннями, що описують реальні технічні системи, однопараметричні, ми також будемо вважати, що група G – однопараметрична.

Для управління важливо, що при лінеаризації близько траєкторії структурна симетрія рівняння (1) не зникає, але замінюється пов'язаною симетрією. Насправді, використовуючи визначення (3) і те, що перетворення симетрії лінійні, отримуємо в лінійній апроксимації для довільних g:

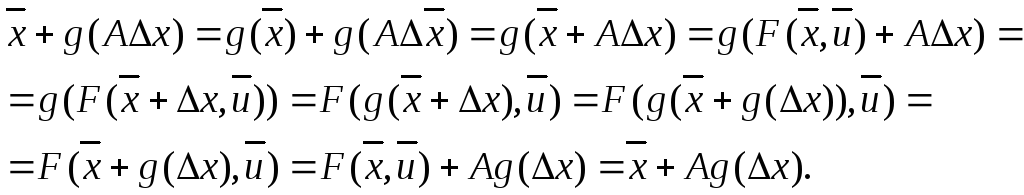
Визначимо L як повну групу симетрій лінеаризованого рівняння (2) автономної системи

Таким чином група L описує динамічну симетрію системи близько програмної траєкторії і включає всі перетворення g. Отже,. Як правило, L співпаде з G. На практиці неможливо визначити незалежно групу G, яка вичерпує динамічні симетрії системи або група L містить "приховані" симетрії. Однак можна показати, що безліч обмежень при визначенні керуючих параметрів може бути отримано на підставі довільної підгрупи. Група у відповідності з інваріантами може бути розкладена:

(4)

з

де – число еквівалентних уявлень в декомпозиції (4), – загальне число інфінітезімальних створюючих в базисі.

1.2. Фазовий портрет динамічної системи. Теорема Такенса

Розглянемо в контексті групового аналізу проблему реконструкції фазового портрету. Основою для реконструкції фазового портрету служать експериментальні дані, отримані в процесі функціонування систем. Необхідно побудувати динамічні рівняння з точністю, необхідної керуючими алгоритмами і виконавчими механізмами. В умовах недоступності повної інформації про стан системи потрібно оцінити структурну і змоделювати динамічну складність по єдиному вимірюваному скалярному виходу. Цей вихід y (t) є функцією невідомого вектора внутрішніх станів s (t) системи:

(5)

Метод, що дозволяє відновлювати простір станів системи та її динаміку, був запропонований Н. Паккардом та ін., він полягає в послідовному вимірі часу виходу y (t) [6]. Алгоритм грунтується на реконструкції станів системи з скалярного вихідного сигналу з використанням тимчасових затримок

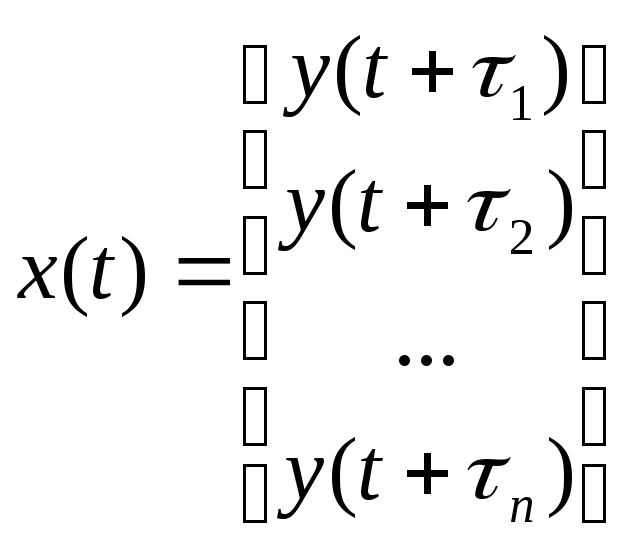. (6)

Ф. Такенс показував [7], що для скалярного вихідного процесу (5), вибраного часу затримки і розмірності n реконструйованого атрактора (, де – хаусдорфова розмірність) ідентифікується відображення , яке забезпечує глобальне взаємно-однозначне уявлення аттрактора.

У результаті застосування методу Паккарда-Такенса відновлюється відображення (1) визначенням стану , де – час послідовних перетинань відповідним чином обраного перерізу Пуанкаре в просторі відновлених станів x(t). Теорема Такенса вводиться для досить загального випадку систем без урахування симетрії, однак вона не задовольняється для більшості технічних систем через слідства наявності симетрії – виродження операторів еволюції. Іншими словами, для таких систем теорема непридатна, тобто простір станів системи не може бути відновлено на підставі єдиного вихідного процесу незалежно від того, яка велика розмірність реконструкції. Більше того, фазовий простір не може бути відновлено ні локально, близько періодичних траєкторій атрактора, ні уздовж певних кривих у просторі фази, ні глобально. Використовуючи мову теорії автоматичного управління, такі системи можна вважати локально і глобально неспостереженими. Питання про непридатність методу реконструкції фазового простору систем, що допускають симетрії, було вперше опрацьовано в роботі [8], де визначено, що причина невдачі застосування теореми Такенса – порушення одного з припущень, що спостережуваний процес, обумовлений рівнянням (5), не має вироджених власних значень для періодичних траєкторій. Однак симетричні системи зазвичай (але не завжди) мають вироджені власні значення через те, що в базисі інваріантів нетривіальні інфінітезімальні утворювання є багатовимірними. Ж. Кінг та І. Стеварт [8] довели узагальнення теореми про вкладення, в якій потрібно, щоб спостережуваний вихід був векторною, а не скалярною функцією стану системи s(t):

(7)

при відображенні простору станів Q ідентифікованої системи в m-мірний евклидовий простір. (На жаль, цей результат в основному проігнорований в працях з нелінійної динаміки.) Стан системи потім може бути аналогічно представлено координатним вектором затримки

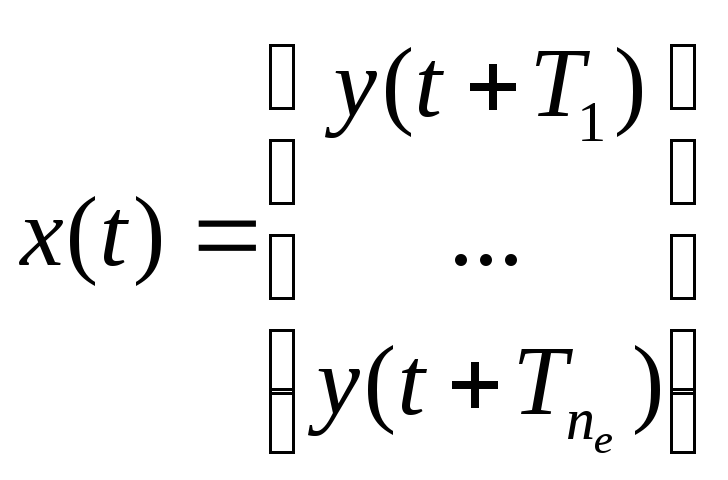, (8)

де тепер розмірність вкладеного простору . Так як вид рівнянь еволюції невідомий, отримати відповідь на питання про можливість побудови функції G можна на підставі властивостей симетрії системи, які часто легко встановити на базі основних перетворень – груп зсуву.

У зв'язку з тим, що для техніки представляє інтерес реконструкція простору станів в рамках лінійного управління, визначимо, що система локально спостерігаюча. Згідно з аналізом, проведеним в [8], для визначення локального вкладення близько періодичної траєкторії s(t) потрібно, щоб у містилася принаймні одна копія кожного інваріантного підпростору , яке отримано однопараметричним розкладанням відповідної групи симетрії . Ця умова повинна виконуватися, щоб допустити, що мінімальна вимір m-мірного вихідного процесу включало утворене інфінітезімальною утворюючою найбільшою розмірності в базисі інваріантів.

Це припущення може бути тривіально визначено на підставі симетрій. Розглянемо незмінний в часі стан . Лінеарізуем вихід (7) в околі цього стану і, позначаючи зсув , отримаємо

, (9)

де матриця C визначена таким чином, що

.

Нагадаємо, що динамічна система, яка визначається рівняннями (2) і (9), або пара (A,C) називається спостерігаючою, якщо протягом будь-якого часу початковий стан може бути визначено з вимірювання керуючих збурень і виходу . В іншому випадку система або пара (A,C) називається неспостережною.

Відомо, що поняття спостережуваності дуальне поняттю керованості: умова спостережуваності для пари (A,C) – еквівалент умови керованості для пари . Наявність групи симетрій безпосередньо мається на увазі, що

,

властивості симетрії матриць A і A* по суті ідентичні (однакові структури спектрів власних значень, жорданових нормальних форм, і т.п.). У результаті відома рангова умова керованості [9], що накладається на матрицю B, повинна також задовольнятися й для матриці C. Ясно, що спостережуваність лінеаризованої системи є еквівалентом спостережуваності власних векторів матриці Якобі вихідної системи. Власний вектор e матриці A спостережуваний, якщо там існує i, , таке, що , де – рядок матриці C.

У випадку, якщо немає випадкового виродження і група T містить щонайбільше одну копію кожного елемента декомпозиції (4) представлення групи , то для того, щоб відновлювати динаміку близько незмінного в часі стану , необхідно, щоб m вимірюваних скалярних вихідних сигналів дорівнювало числу параметрів . Це означає, що при існуванні симетрії зсуву динаміка системи (1) може бути змодельована системою (2), при цьому розмірність вектора параметрів дорівнює , а самі параметри можуть бути породжені груповий операцією зсуву по часу і, отже, являють собою лінійні функції часу.