Примитивно-рекурсивные функции.

Формальное индуктивное определение примитивно-рекурсивной функции следующее:

Базисные функции для всех натуральных n, m, где nm являются примитивно-рекурсивными;

• если g₁(x₁,…, x_n), …g_m(x₁,…, x_n), h(x₁,…, x_m) - примитивно-рекурсивные функции, то Sⁿ_m(h, g₁,…, g_m) - примитивно-рекурсивные функции для любых натуральных n, m;

• если g(x₁,…, x_n) и h(x₁,…, x_m, у, z) - примитивно-рекурсивные функции, то R_n(g, h) – примитивно-рекурсивная функция;

• других примитивно-рекурсивных функций нет.

Поскольку исходные функции являются вычислимыми, а операторы суперпозиции и примитивной рекурсии вычислимость сохраняют, то множество всех примитивно-рекурсивных функций есть подкласс класса всех вычислимых (рекурсивных) функций.

Очевидно, что класс всех примитивно-рекурсивных функции: счётен, т.к. каждая такая функция задаётся описанием её построения из базисных функции; всюду определён.

Практически все арифметические функции, употребляемые в математике по конкретным поводам, являются примитивно рекурсивными.

Пример:

Функция – примитивно-рекурсивная, т.к. (всего n раз).

Пример:

Функция - примитивно-рекурсивная, т.е.

Замечание:

Схемной интерпретацией примитивной рекурсии может быть конечный автомат:

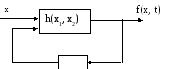
Эта схема состоит из элемента, вычисляющего за один такт функцию h от двух переменных и элемента задержки на один такт. По каналам схемы могут передаваться натуральные числа. Время t считается дискретным, то есть t=0, 1, 2, 3…. Схема имеет один вход х и один выход f. Выход f зависит не только от х, но и от момента t, в котором он рассматривается. В начальный момент t=0 второй вход h является константой с, зависящей от начального состояния схемы: f(x, 0)=h(x, c)=g(x). В момент t=1: f(x, 1)=h(x, f(x, 0)); в общем случае f(x, t+1)=h(x, f(x,t)). Нетрудно убедиться, например, что если h выполняет умножение, а с=1, то f(x, t)=x^t+1.

Поскольку исходные (базисные) функции являются вычислимыми, а операторы суперпозиции и примитивной рекурсии вычислимость сохраняют, то множество всех примитивно-рекурсивных функций есть подкласс класса всех вычислимых функций;

Класс всех примитивно-рекурсивных функций счетен, поскольку каждая такая функция задается описанием ее построения из исходных функций.

Практически все арифметические функции, употребляемые в математике по конкретным поводам, являются примитивно-рекурсивными функциями, например: х+у, х*у, х^у и т.д.

Алгоритмическая система а.А.Маркова.

Всякий словарный алгоритм U имеет дело с некоторым алфавитом А, а решение конкретной задачи сводится к переработке слов в данном алфавите по некоторым заранее заданным правилам . Такой подход в теории алгоритмов развит А.А.Марковым, предложившим концепцию нормального алгорифма в качестве математической модели понятию вычислительной процедуры.

Нормальные алгорифмы U=<A, > - класс словарных алгоритмов, то есть алгоритмов (применимых к словам некоторого алфавита А), элементарными действиями которых являются подстановки в слова (их кортеж есть схема ).

Всякий нормальный алгоритм, являясь алгоритмом в некотором алфавите А, порождает в нем детерминированный процесс переработки слов. Поэтому любой нормальный алгоритм в фиксированном алфавите А вполне определяется указанием его схемы  - упорядоченного конечного списка формул подстановки в А. Каждая такая формула по существу представляет пару <_i,_i > слов в А (то есть _i, _i А^*). Слово _i называется левой частью этой формулы, а _i – ее правой частью. Среди формул данной схемы некоторые выделяются специально и объявляются заключительными. Обычно в схеме нормального алгоритма заключительная формула записывается в виде _i  _i (, а незаключительная в виде _i  _i. При этом допустимы формулы вида : e_i ; _i eee_i ee_i; (e – пустое слово)

Нормальный алгоритм U в алфавите А есть предписание строить, исходя из произвольного слова P в А (PА^*), последовательность слов _i.

В свете изложенного алгоритмическая система «нормальный алгорифм» имеет вид:

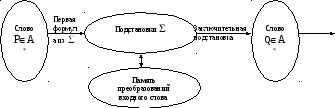
Применением нормального алгоритма U к слову  называется процесс, определяемый следующим правилом (представляющим собой алгоритм выполнения нормального алгоритма):

1. Считать, что i=1. Перейти к пункту 2.

2. Проверить, поддается ли преобразуемое слово i-ой формуле. Если да, то перейти к пункту 3, если нет – к пункту 5.

3. Первое простое вхождение левой части i-ой формулы в преобразуемом слове заменить правой частью i-ой формулы. Результат считать в дальнейшем преобразуемым словом, перейти к пункту 4.

4. Если i-ой формула является заключительной подстановкой, то процесс прекратить. В противном случае перейти к пункту 1.

5. Проверить, имеет ли место равенство i=n. Если да, то процесс прекратить, в противном случае перейти к пункту 6.

6. Увеличить значение i на 1 и перейти к пункту 2.

Любое слово P в алфавите А может служить исходными данными для нормального алгоритма в алфавите А. При этом возможны случаи:

• Процесс выполнения нормального алгоритма для слова А^* заканчивается формулой _i _i после конечного числа шагов. При этом говорят, что нормальный алгоритм применим к слову , и полученное после его выполнение слово ^* называется результатом.

• Процесс выполнения нормального алгоритма при исходном слове А^* никогда не заканчивается или происходит безрезультативная остановка (то есть не на формуле _i _i). В этом случае говорят, что нормальный алгоритм не применим к слову .

Пример:

Алгоритм U=             «обращает» любое слово в А, то есть перерабатывает его в слово, записанное в обратном порядке (его можно записать как 100 с тем, чтобы использовать ).

Так, слово 100 этот нормальный алгоритм последовательно перерабатывает в слова   010, 001, 001, 001, 001, 001, 001, 001, 001, 001, 001, 001, 001.

Замечание:

Последний член этой последовательности считается результатом применения алгоритма U к слову =100 и обозначается символом U(). При этом считается, что U перерабатывает =100 в =001, и пишут U()= (в нашем примере U(100)=001).

Пример:

Алгоритм U=<a, b, <a b; baaba, aa> реализует предписание: «Взяв какое-либо слово a, b^* в качестве исходного, (где а, ba, aa), делай допустимые переходы до тех пор, пока не получится слово вида aa, тогда остановись: слово и есть результат».

Так, взяв слово babaa в качестве исходного данного после первого перехода (то есть применив формулу ba aba ), получим baaaba (здесь =baa), а после второго (то есть применив снова формулу ba aba) имеем aabaaba (здесь =ааba). Применив формулу aa к слову aabaaba получим результат baaba (то есть U(babaa)=baaba).

Однако, взяв в качестве исходного данного слова =baaba, получим бесконечную последовательность abaaba, baabab, abababa, bababab, babababa, … в которой не будет слова aa. Это означает, что алгоритм U не будет применим к слову =baaba.

Если же исходным данным взять слово abaab, то получим конечную последовательность baabb, abbaba, bbabab, в которой к последнему слову нельзя применить допустимый переход, то есть это случай безрезультативной остановки (это означает также неприменимость заданного алгоритма U к слову abaab).

Считается, что для любого алгоритма В в алфавите А может быть построен нормальный алгоритм U над этим алфавитом, перерабатывающий произвольное слово А^* в тот же самый результат, в который перерабатывает его исходный алгоритм В. Это соглашение известно в теории алгоритмов под названием принципа нормализации.

В этом плане уточнения понятия алгоритм алгоритмическими системами А.Маркова, А.Черча и А.Тьюринга являются эквивалентными.

Дальнейшее уточнение понятия алгоритма связано с ассоциативным исчислением, которое является множеством всех слов в некотором алфавите вместе с какой-нибудь конечной системой допустимых подстановок.