
- •Елементи лінійної алгебри
- •Елементи аналітичної геометрії
- •6.Скалярний добуток.
- •Комплексні числа
- •Вступ до математичного аналізу
- •Рекомендована література
- •§ 1.1. Матриці.
- •§ 1.2. Визначники.
- •§ 1.3. Обернена матриця. Ранг матриці.
- •§ 1.4. Системи лінійних рівнянь. Метод Гаусса.
- •§ 1.5. Невироджені системи лінійних рівнянь. Матричний метод. Ф ормули Крамера.
- •§ 1.6. Критерій сумісності та загальна схема дослідження і розв’язування системи лінійних рівнянь.
- •§ 1.7. Однорідні системи лінійних рівнянь.
- •II. Елементи аналітичної геометрії.
- •§ 2.1. Декартова прямокутна система координат.
- •§ 2.2. Означення векторної велечини. Основні поняття.
- •§ 2.3. Лінійні операції над векторами.
- •§ 2.4. Лінійна залежність векторів. Базис.
- •§ 2.5. Скалярний добуток векторів. Кут між векторами.
- •§ 2.6. Векторний добуток векторів.
- •§ 2.7. Мішаний добуток векторів.
- •§ 2.8. Пряма на площині.
- •§ 2.9. Площина у просторі.
- •§ 2.10. Пряма у просторі.
- •§2.11. Пряма й площина. Нехай у просторі задані пряма
- •§2.13. Гіпербола.
- •§2.14. Парабола.
- •§2.15. Загальне рівняння кривої другого порядку та його перетворення до канонічної форми.
- •§ 2.16. Полярна система координат. Параметричні рівняння лінії.
- •§ 2.17. Поверхні другого порядку.
- •7. Конічні поверхні.
- •§ 2.18. Загальне рівняння поверхні другого порядку та його спрощення у деяких частинних випадках.
§ 2.6. Векторний добуток векторів.
Упорядкована
трійка ненульових векторів
![]() називається правою, якщо після
зведення її до спільного початку для
спостерігача, що знаходиться на кінці
вектора
називається правою, якщо після
зведення її до спільного початку для
спостерігача, що знаходиться на кінці
вектора![]() ,
поворот на найменший кут від вектора
,
поворот на найменший кут від вектора
![]() до вектора
до вектора
![]() здійснюється проти руху годинникової
стрілки (рис.8).
здійснюється проти руху годинникової
стрілки (рис.8).
Векторним
добутком двох неколінеарних векторів
![]() і
і
![]() називається вектор
називається вектор
![]() ,
який визначається наступними трьома
правилами:
,
який визначається наступними трьома
правилами:
-
довжина вектора
 задається формулою
задається формулою
![]() ,
,
![]() (6.1)
(6.1)
де
![]() – кут між векторами
– кут між векторами
![]() і
і
![]() ;
;
-
вектор
 перпендикулярний до кожного з векторів
перпендикулярний до кожного з векторів
 і
і
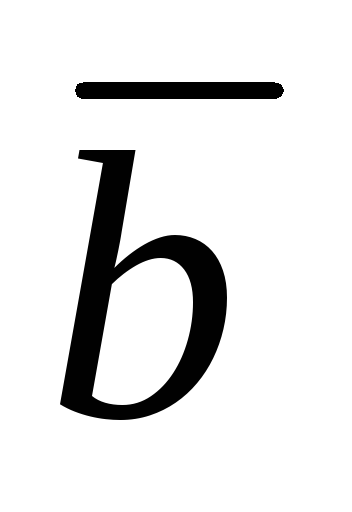 ;
; -
вектори
 утворюють праву трійку векторів (рис.8).
утворюють праву трійку векторів (рис.8).
Перше
правило визначає довжину вектора
![]() ,
а два останні –його напрям. Легко бачити,
що добуток правої частини формули (6.1)
дорівнює площі паралелограма,
побудованого на векторах
,
а два останні –його напрям. Легко бачити,
що добуток правої частини формули (6.1)
дорівнює площі паралелограма,
побудованого на векторах
![]() і
і
![]() .
Отже, довжина вектора
.
Отже, довжина вектора
![]() дорівнює площі вказаного паралелограма.
дорівнює площі вказаного паралелограма.
Вважається, що векторний добуток двох колінеарних векторів дорівнює нульовому вектору.
Векторний
добуток векторів
![]() і
і
![]() будемо позначати
будемо позначати
![]() або
або
![]() .
.
Властивості векторного добутку:
-
 ;
; -
 ;
; -
 ;
; -
якщо векторний добуток двох ненульових векторів
 і
і
 дорівнює нульовому вектору, то вектори
дорівнює нульовому вектору, то вектори
 і
і
 колінеарні.
колінеарні.
Нехай
вектори
![]() і
і
![]() задані своїми координатами:
задані своїми координатами:
![]()
![]()
Тоді:
 ,
(6.2)
,
(6.2)
або
![]() .
(6.3)
.
(6.3)
Площа
паралелограма й площа трикутника,
побудованих на векторах
![]() і
і
![]() ,
обчислюються наступним чином:
,
обчислюються наступним чином:
![]()
![]() ,
,
![]() .
(6.4)
.
(6.4)
Приклад
1. Задані два вектори
![]() і
і
![]() .
Знайти: а) вектор, перпендикулярний до
кожного з векторів
.
Знайти: а) вектор, перпендикулярний до
кожного з векторів
![]() і
і
![]() ;
б) площу трикутника, побудованого на
векторах
;
б) площу трикутника, побудованого на
векторах
![]() і
і
![]() .
.
Розв’язання. а) Відмітимо, що задача не має єдиного розв’язку, тобто існує нескінченне число колінеарних векторів, які задовольняють умовам цієї задачі. Одним із таких векторів є векторний добуток (див. означення):

![]() .
.
б) Використовуючи (6.4), здобудемо
![]() (кв.
од.).
(кв.
од.).
§ 2.7. Мішаний добуток векторів.
Скалярний
добуток векторів
![]() і
і
![]() називається мішаним добутком
векторів
називається мішаним добутком
векторів
![]() і позначається
і позначається
![]() або
або
![]() .
Таким чином, у відповідності з означенням,
можемо записати
.
Таким чином, у відповідності з означенням,
можемо записати
![]() . (7.1)
. (7.1)
Властивості мішаного добутку:
1) мішаний добуток не змінюється, якщо в ньому поміняти місцями операції векторного й скалярного добутку:
![]()
2) мішаний добуток не змінюється при циклічній перестановці векторів:
![]()
3) при перестановці місцями будь–яких двох векторів мішаний добуток змінює знак на протилежний:
![]()
![]()
![]()
Якщо
вектори
![]()
![]() і
і
![]() задані своїми координатами, то
задані своїми координатами, то
 (7.2)
(7.2)
Модуль
мішаного добутку некомпланарних векторів
![]() дорівнює об’єму паралелепіпеда,
побудованого на цех векторах. Отже об’єм
паралелепіпеда й піраміди, побудованих
на векторах
дорівнює об’єму паралелепіпеда,
побудованого на цех векторах. Отже об’єм
паралелепіпеда й піраміди, побудованих
на векторах
![]() можуть бути знайдені за формулами:
можуть бути знайдені за формулами:
![]()
![]() (7.3)
(7.3)
Приклад
1. Точки
![]()
![]()
![]()
![]() є вершинами чотирикутної піраміди.
Знайти її об’єм.
є вершинами чотирикутної піраміди.
Знайти її об’єм.
Розв’язання.
![]()
![]()
![]()

![]() (куб.
од).
(куб.
од).
Використовуючи
поняття мішаного добутку, умову
компланарності (лінійної залежності)
трьох ненульових векторів
![]() можна представити у вигляді
можна представити у вигляді
![]() (7.4).
(7.4).
Якщо мішаний добуток трьох ненульових векторів відмінний від нуля, то ці вектори утворюють базис у просторі (лінійно незалежні).
Приклад
2. При якому значенні параметра
![]() вектори
вектори
![]()
![]() і
і
![]() компланарні ?
компланарні ?
Розв’язання. Використовуємо умову компланарності (7.4):
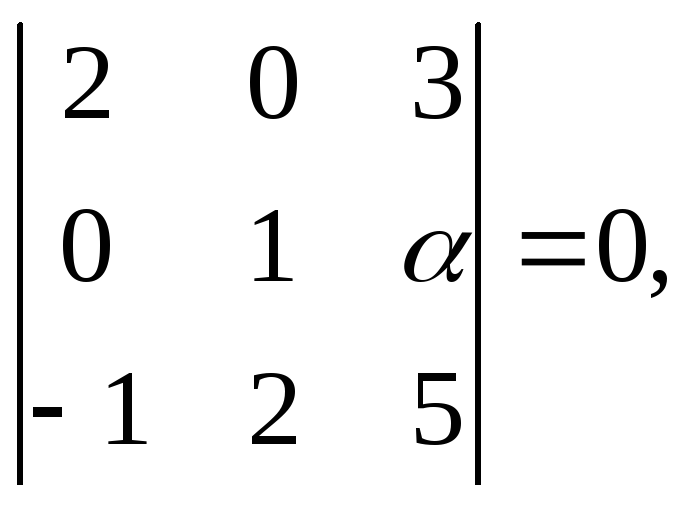
![]()
