§ 2.10. Пряма у просторі.

Наведемо основні рівняння прямої у просторі у прямокутній системі координат .

Загальні рівняння:

(10.1)

Пряма (10.1) є прямою перетину двох непаралельних площин і.

Канонічні рівняння:

, (10.2)

де – координати даної точки, яка належить прямій; – координати даного ненульового вектора , який паралельний прямій. Вектор називається напрямним вектором прямої.

Приклад 1. задані точки , , . Знайти рівняння прямої, що проходить через точку паралельно вектору .

Розв’язання. Знайдемо координати напрямного вектора (вектора ) і застосуємо формулу (10.2):

; .

Рівняння прямої, що проходить через дві дані точки:

, (10.3)

де ; – координати двох даних точок, через які проходить пряма.

Параметричні рівняння:

 

де – координати даної точки, що належить прямій; – координати даного напрямного вектора прямої.

Нехай задані загальні рівняння (10.1). Для того щоб здобути канонічні рівняння (10.2), необхідно визначити координати деякої точки , яка належить прямій і координати напрямного вектора . Одну з координат точки задаємо довільно (нас влаштовує будь-яка точка прямої). Підставляємо цю координату в рівняння (10.1) і розв’язуємо систему двох лінійних рівнянь із двома невідомими. За напрямний вектор можна взяти векторний добуток нормалей і даних площин, тобто (цей вектор перпендикулярний до нормалей обох площин, а, отже, паралельний прямій їх перетину).

Для того щоб від канонічних рівнянь (10.2) перейти до параметричних (10.4) потрібно кожен дріб формули (10.2) прирівняти до параметра і розв’язати здобуті рівняння відносно змінних відповідно.

Приклад 2. Пряма задана загальними рівняннями

Знайти канонічні та параметричні рівняння цієї прямої.

Розв’язання. Знайдемо спочатку координати деякої точки прямої. Нехай . Тоді:



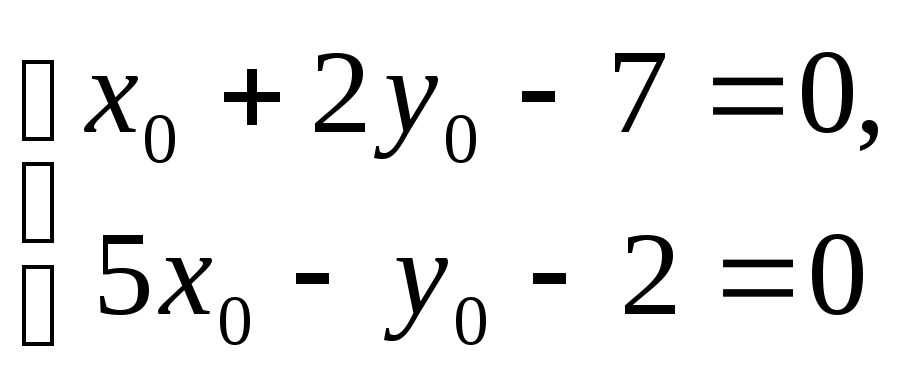
Знайдемо напрямний вектор прямої:

.

Запишемо канонічні рівняння прямої, яка проходить через точку і паралельна вектору :

.

Знайдемо параметричні рівняння:

_{, ,} ;

_{, ,} .

§2.11. Пряма й площина. Нехай у просторі задані пряма

(11.1)

і площина

. (11.2)

Кутом між прямою й площиною називається гострий кут між прямою і її проекцією на цю площину. Кут між прямою (11.1) і площиною (11.2) визначається за формулою

. (11.3)

Умова паралельності прямої й площини (умова перпендикулярності нормалі і напрямного вектора ):

. (11.4)

Умова перпендикулярності прямої й площини (умова паралельності нормалі і напрямного вектора ):

. (11.5)

Якщо умова (11.4) не виконується, то пряма з площиною перетинаються й мають одну спільну точку. Один із методів знаходження координат точки перетину прямої й площини розглянемо на наступному прикладі.

Приклад 1. Пряма й площина задані відповідно рівняннями

, .

Знайти: а) кут між прямою й площиною; б) точку перетину прямої й площини.

Розв’язання. а) Застосувавши формулу (11.3), маємо

;

.

б) Запишемо параметричні рівняння прямої:

_{, ,} ;_{, ,} .

Останні рівняння визначають координати будь-якої точки прямої через параметр (кожному дійсному значенню відповідає своя точка на прямій і навпаки). Знайдемо значення , при якому координати точки прямої будуть задовольняти, також, і рівнянню площини (підставляємо відповідні вирази для в рівняння площини):

,  .

Використовуючи параметричні рівняння прямої, обчислюємо координати точки перетину:

, , .

§2.12. Еліпс

Еліпсом називається множина точок площини, які мають наступні властивості: сума відстаней від будь-якої точки цієї множини до двох даних точок площини є величина стала і більша за відстань між даними точками. Дві дані точки називаються фокусами еліпса і позначаються і .

Використовуючи означення, легко здобути рівняння еліпса. Систему координат розміщуємо наступним чином: вісь проходить через фокуси і , а вісь – посередині між ними (рис.11).

Відстань між фокусами і позначимо через , а суму відстаней від довільної точки еліпса до фокусів – через . У відповідності з означенням, можемо записати

. (12.1)

Підставивши в (12.1) відповідні вирази і, зробивши деякі перетворення, здобудемо

, (12.2)

де . Рівняння (12.2) називається канонічним рівнянням еліпса: величини і ( і ) – відповідно більшою й меншою осями (напівосями) еліпса. На основі рівняння (12.2) можна побудувати саму криву (рис.12).

Якщо фокуси еліпса розміщені на осі симетрично відносно осі , то рівняння (12.2) також буде його канонічним рівнянням, але у цьому випадку .

У граничному випадку, коли (), рівняння (12.2) приймає вигляд

. (12.3)

Останнє рівняння є рівнянням кола з центром у початку координат і радіусом .

Ексцентриситетом еліпса називається відношення відстаней між фокусами до більшої осі:

, (); , (). (12.4)

Ексцентриситет еліпса характеризує відносну різницю між його осями і задовольняє співвідношенню . Для еліпса, у якого вказана різниця невелика (), значення близьке до нуля (у кола ). Якщо ж указана різниця велика ( або ), то близьке до одиниці.

Приклад 1. Для еліпса

знайти: а) напівосі; б) координати фокусів; в) ексцентриситет.

Розв’язання. а) Порівнявши дане рівняння з рівнянням (12.2), маємо

, ; , .

б) Так як , то , . Отже, , – фокуси еліпса.

в) На основі (12.4), знайдемо .