ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Неопределенные, определенные и несобственные интегралы. Приложения
Учебно-методическое пособие для вузов.
Составители: А.Д. Баев,
Е.В. Петрова,
В.В. Провоторов
ВОРОНЕЖ
2006
Утверждено научно-методическим советом математического факультета
07.09.2006 Года
Протокол №1
Составители: Баев А.Д., Петрова Е.В., Провоторов В.В.
Учебно-методическое пособие подготовлено на кафедре уравнений
в частных производных и теории вероятностей
математического факультета Воронежского госуниверситета
Рекомендуется для студентов 1 курса дневного отделения
химического факультета для специальности «Химия» 020101 (011000).
1. Классы интегрируемых функций
1.1. Многочлен степени
Рассмотрим многочлен степени n:
(1)
Здесь как
коэффициенты, так и значения переменной
могут быть как действительными, так и
комплексными.
Каждое
действительное или комплексное значение
,
которое обращает
в нуль, называется корнем этого многочлена:
.
Следовательно, корни многочлена (1) представляют собой решения алгебраического уравнения n – ой степени:
.
Формула Тейлора применима как для действительных многочленов, так и для многочлена (1):
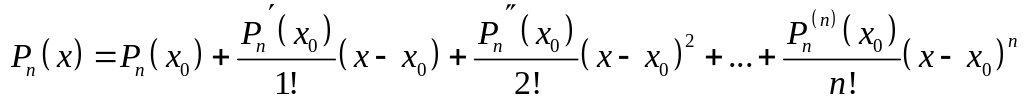. (2)
Теорема
Безу. Для того, чтобы многочлен
имел корень
,
необходимо и достаточно, чтобы он делился
на
,
т.е. был представим в виде (3).
Определение.
Если
,
а
,
то корень
называется простым.
В этом случае
в формуле (3)
и, согласно теореме Безу, его нельзя
разделить на
.
Если
,
,
,
то
называется корнем кратности k.
Тогда формула Тейлора для по степеням имеет вид:
.
,
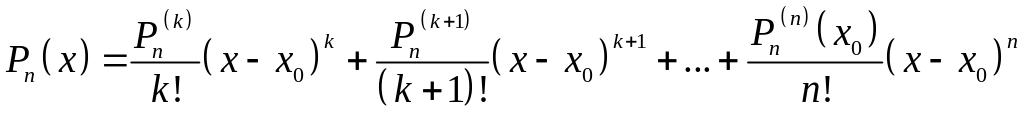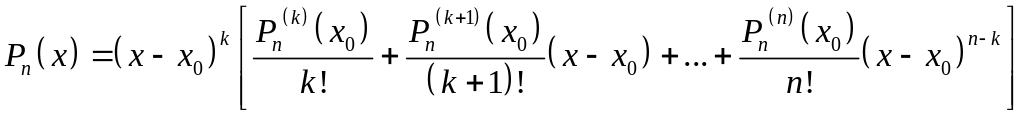
где
. (4)
Если
есть корень многочлена
кратности k, то многочлен
делится на
.
Если значения
двух многочленов совпадают для всех
,
то эти многочлены имеют одинаковые
коэффициенты.
Действительно,
из (2) следует, что если
,
то коэффициенты обоих многочленов будут
вычисляться по одним и тем же формулам:
.
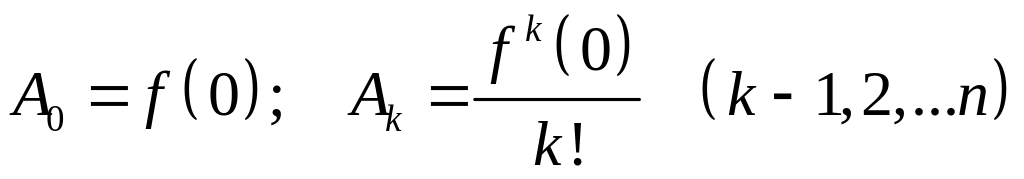Теорема.
Всякий многочлен степени
имеет, по крайней мере, один действительный
комплексный корень.
Замечание.
Неалгебраическое уравнение может не
иметь ни действительных, ни комплексных
корней. Например:
.
Действительно,
при любом комплексном
.
Следствие. Многочлен степени имеет корней с учётом их кратности, т.е. представим в виде произведения:
(5)
где
– различные корни многочлена
кратности
(
).
Некоторые (или все) корни могут быть
комплексными.
Если
и к многочлену степени
снова применяем основную теорему.
Обозначим корень этого многочлена через
,
а его кратность через
.
В результате получим:
.
Процесс закончится через конечное число шагов (не большего n) и мы придем к формуле (5).
Если в правую часть (5) подставить вместо х число, отличное от , то она не обратится в нуль. Это показывает, что других корней, кроме найденных, многочлен не имеет и представление (5) единственно.
Все сказанное до сих пор относится к многочленам, как с действительными, так и с комплексными коэффициентами. Пусть теперь многочлен имеет действительные коэффициенты и пусть у него имеется комплексный корень кратности s:
.
Оказывается,
что если коэффициенты действительны,
то и число
тоже будет корнем той же кратности.
Т.е. в этом случае комплексные корни многочлена являются комплексно – сопряжёнными.
Рассмотрим множители:
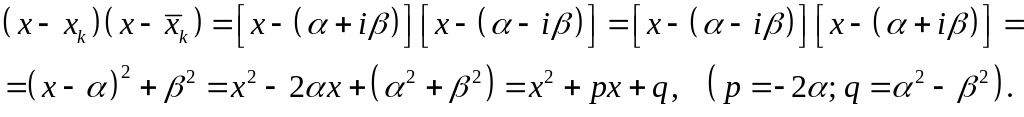
Следовательно, объединяя скобки, соответствующие комплексно - сопряженными корнями в выражении (5), многочлен степени n с действительными коэффициентами можно разложить только на действительные множители – линейные и квадратичные:
где, все трёхчлены не имеют действительных корней.
Если многочлен не имеет комплексных корней, то квадратичные множители будут отсутствовать.