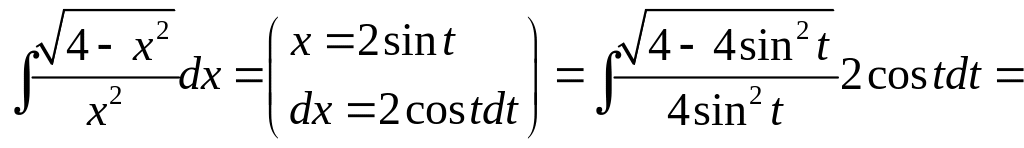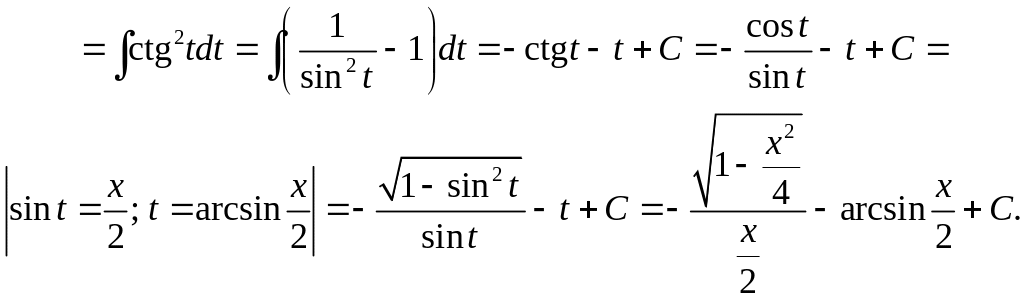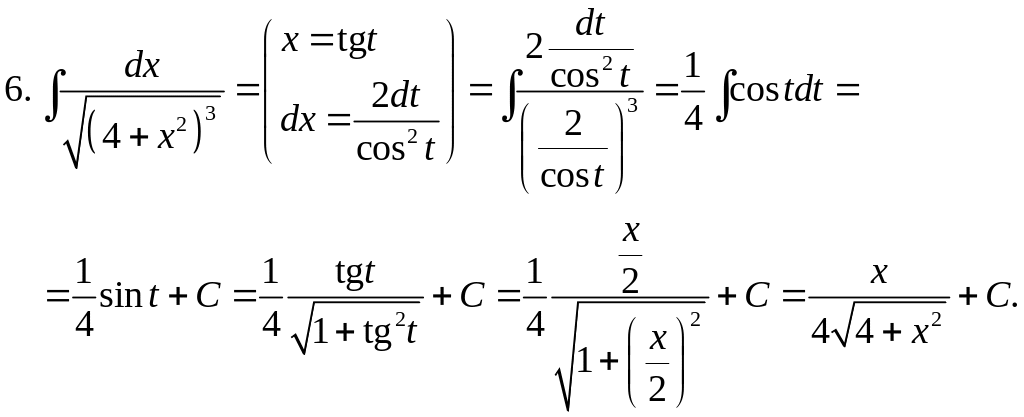2.7. Интегрирование правильных рациональных дробей
Пример
1. Вычислить интеграл
.
Подынтегральная функция представляет собой рациональную дробь. Разложим ее на сумму простейших дробей.
.
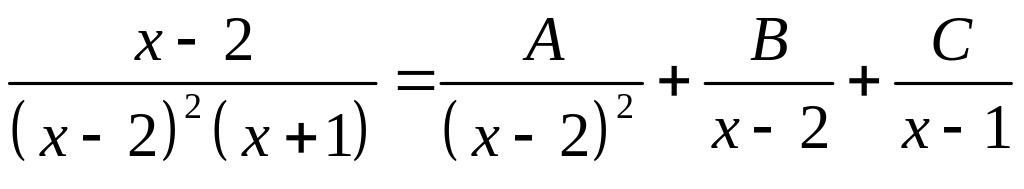Приведем правую часть равенства к общему знаменателю и приравняем числители.
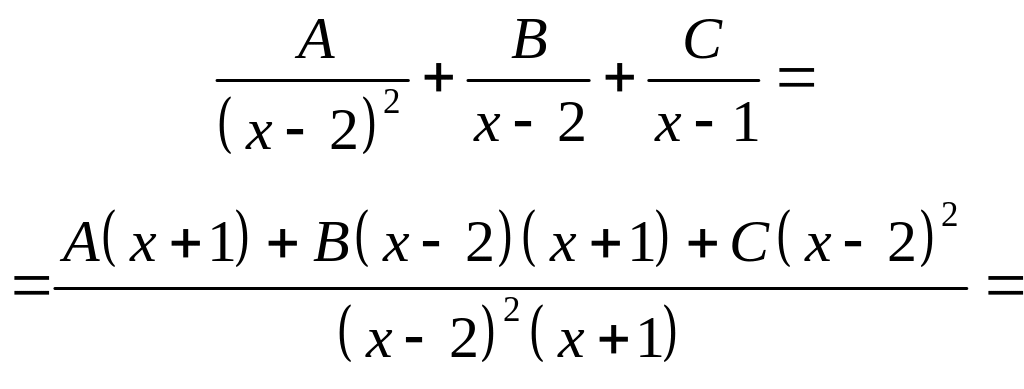
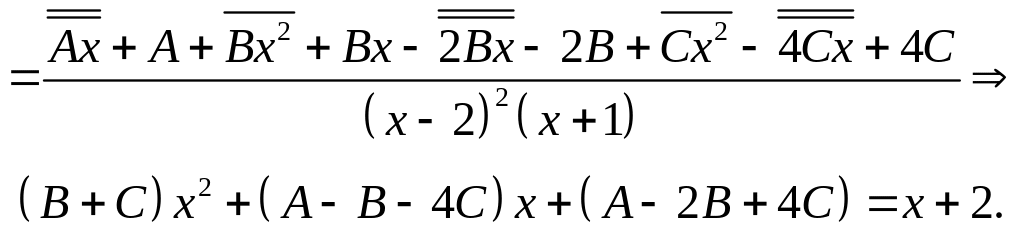
Два многочлена тождественно равны тогда и только тогда, когда они имеют одинаковые степени и коэффициенты при одинаковых степенях равны:
.
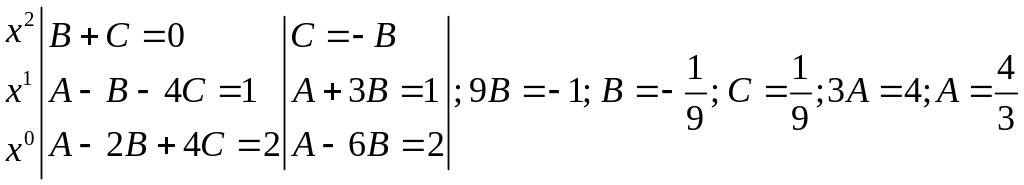Подставим найденные коэффициенты в разложение
.
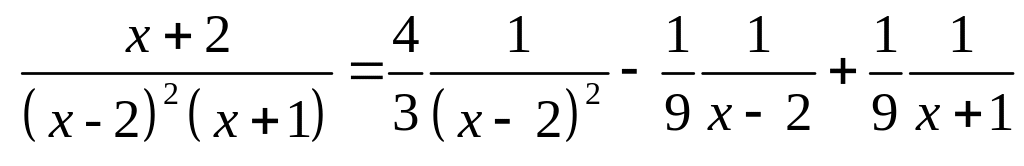Окончательно получим:
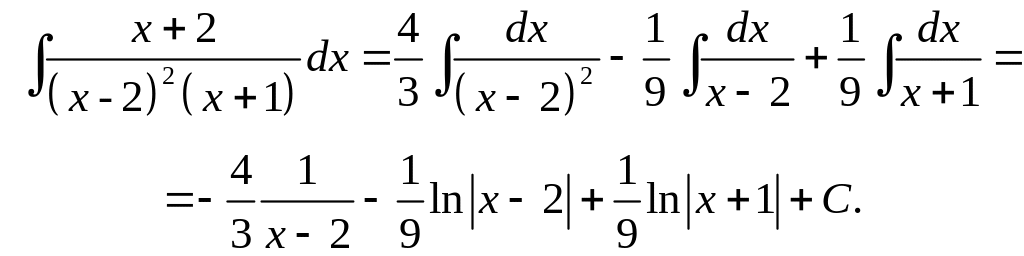
Пример
2. Вычислить
.
;
;
;
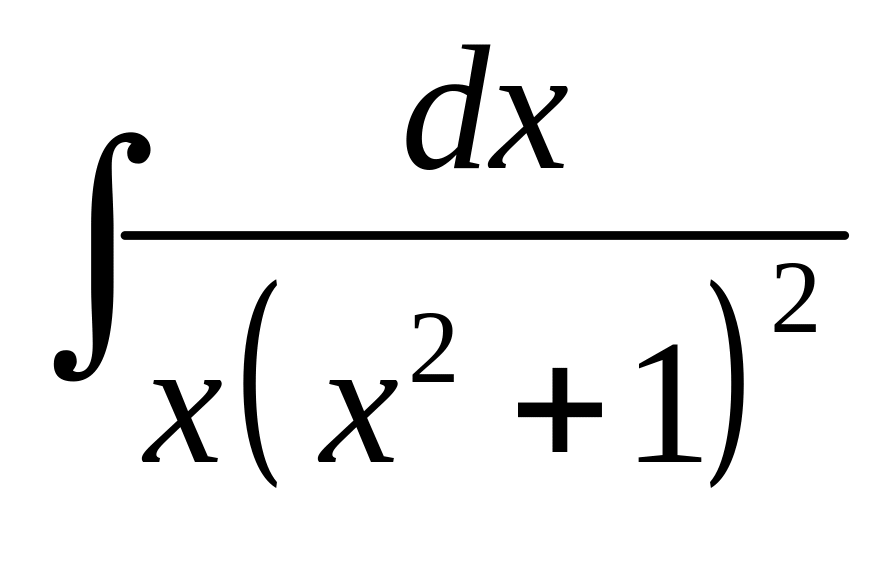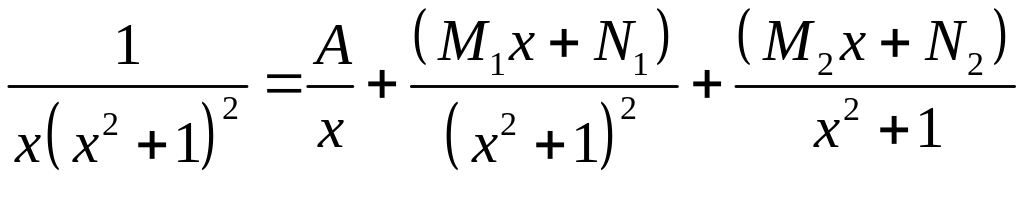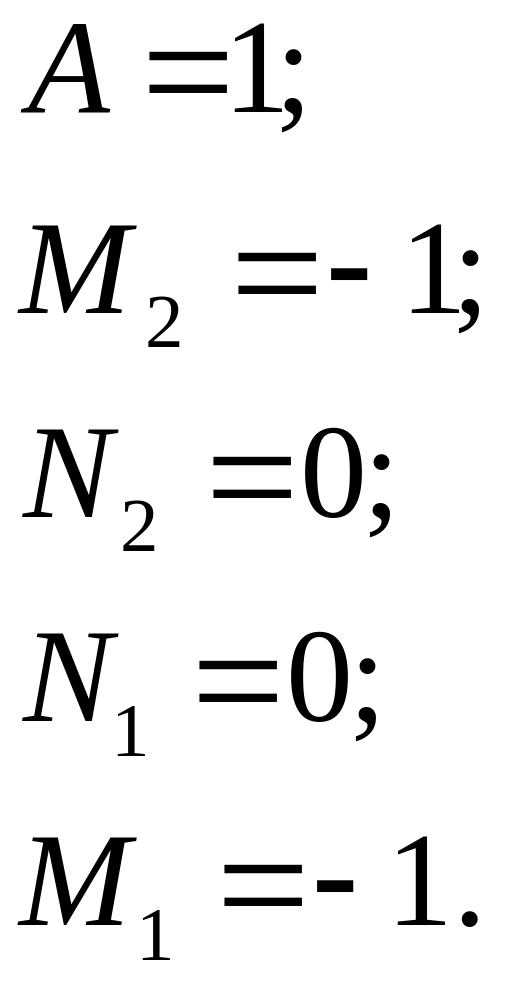
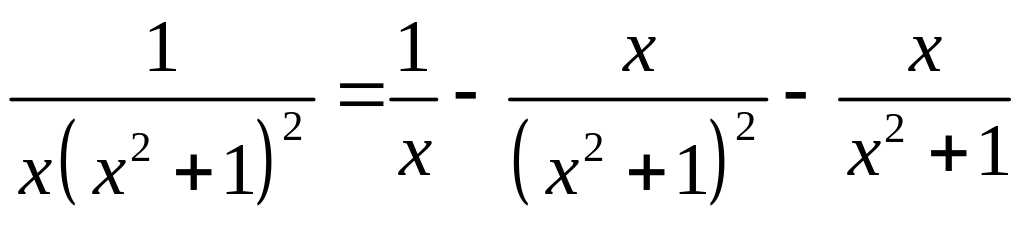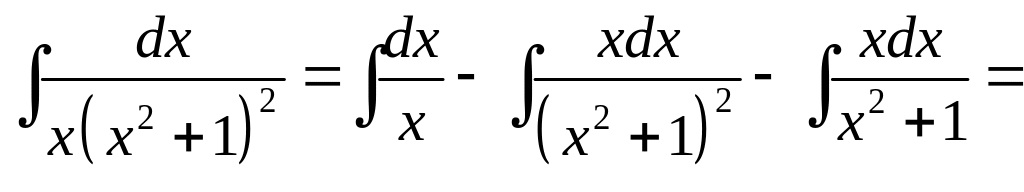
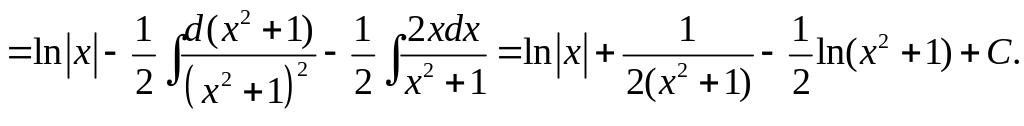
Заключение. Всякая рациональная функция интегрируется в элементарных функциях, причем в результате получаются многочлены, дробно-рациональные функции, логарифмы и арктангенсы.
Замечание.
Чтобы интегрирование функции (6) довести
до конца, нужно знать все корни многочлена
и их кратности. В принципе метод разложения
на сумму простейших дробей применим
всегда, но он связан часто с необходимостью
решать алгебраические уравнения высоких
степеней, что не всегда возможно.
2.8. Интегрирование тригонометрических функций
1.Универсальная тригонометрическая подстановка
Пусть
надо вычислить интеграл от тригонометрической
функции, рациональной относительно
и
:
. (14)
Докажем, что с помощью замены переменной вычисление данного интеграла можно свести к вычислению интеграла от дробно-рациональной функции относительно . Положим:
. (15)
Выразим
,
и
через
и
;
;
;
.
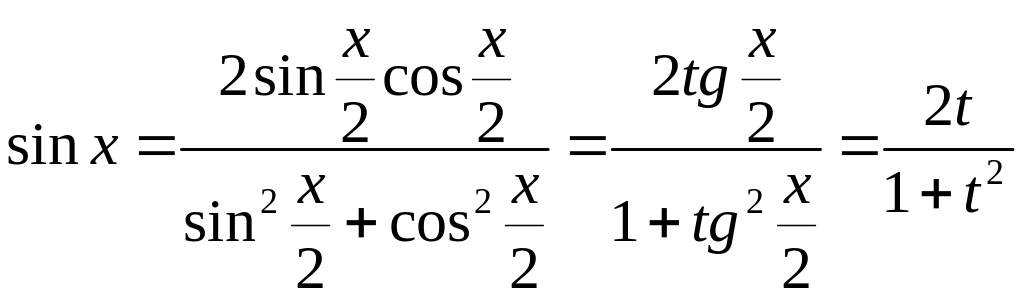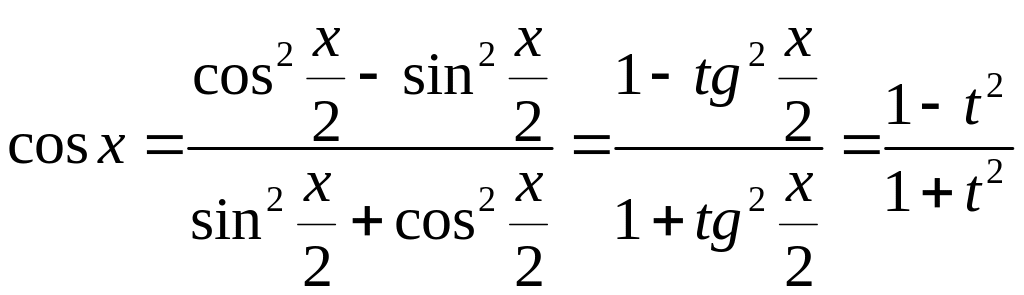Следовательно,
.
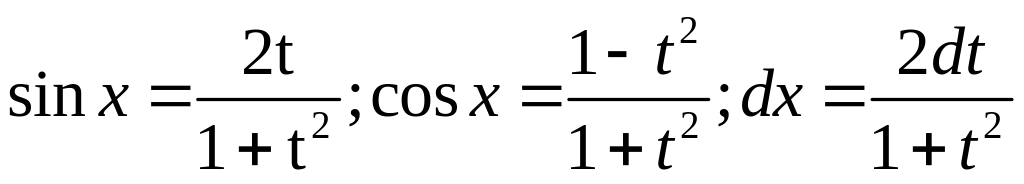Получаем:
.
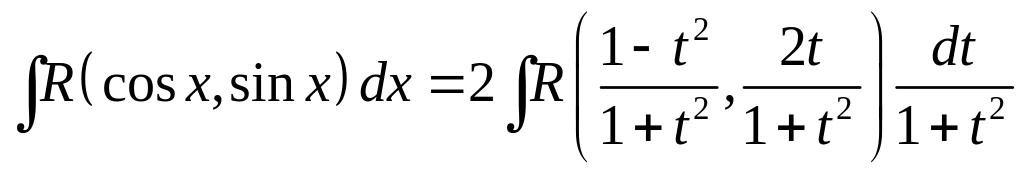Под знаком интеграла получим дробно-рациональную функцию от . Это означает, что рациональное тригонометрическое выражение всегда интегрируемо в конечном виде.
Примеры. Вычислить:
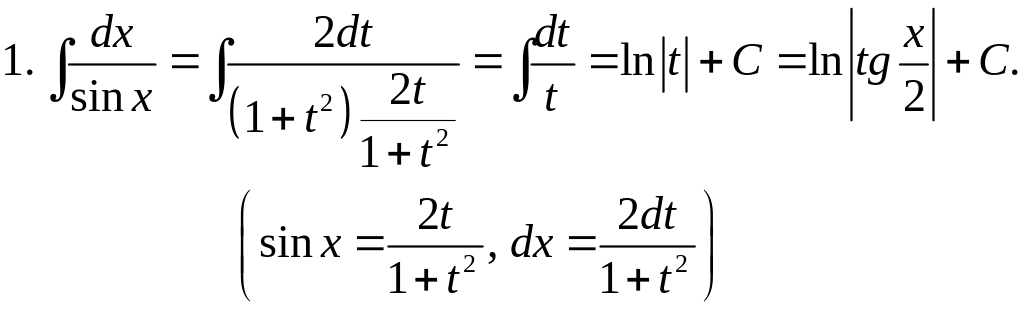
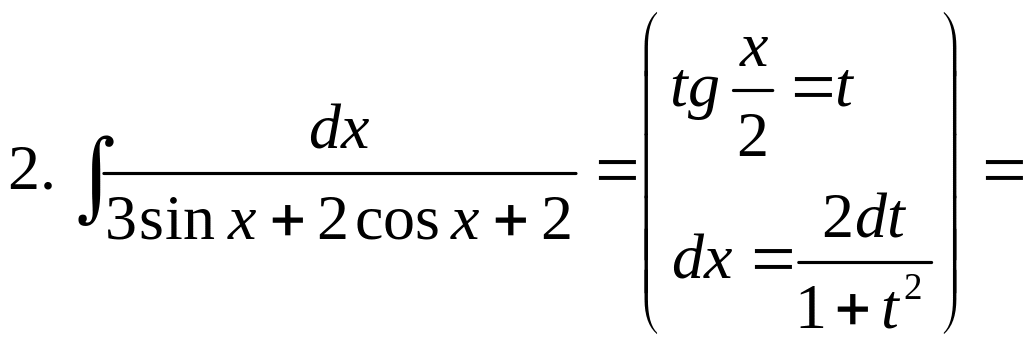
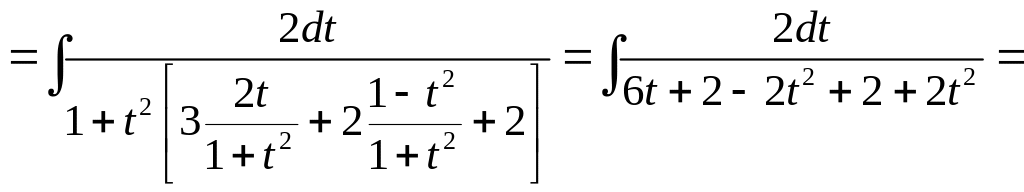
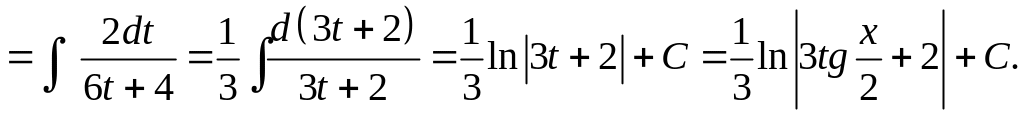
Замена переменной (15) называется универсальной тригонометрической подстановкой, т.к. с ее помощью интеграл (14) всегда приводится к интегралу от дробно-рациональной функции. Однако пользоваться этой подстановкой не всегда целесообразно, так как часто она приводит к громоздким выкладкам. Поэтому в некоторых частных случаях используют другие подстановки.
2.Частные случаи интегрирования тригонометрических выражений.
1) Если
подынтегральная функция нечетна
относительно
:
,
тогда замена
рационализирует интеграл (14).
Пример.
3.
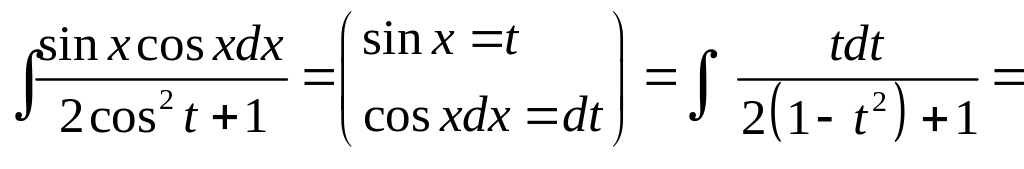
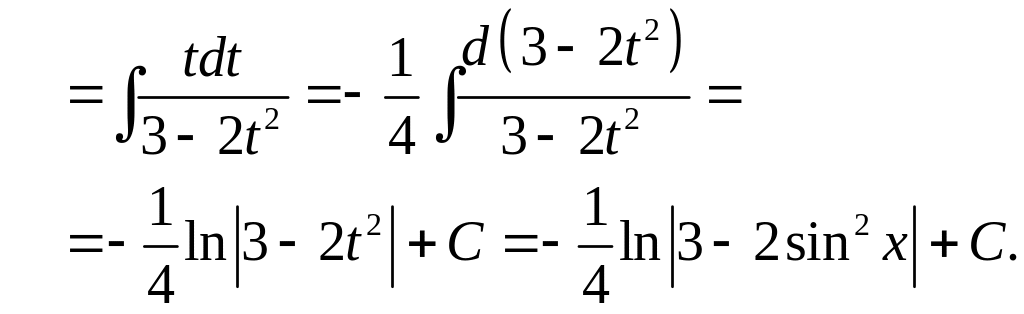
2) Если
подынтегральная функция нечетна
относительно
:
,
тогда замена
рационализирует интеграл (14).
Пример.
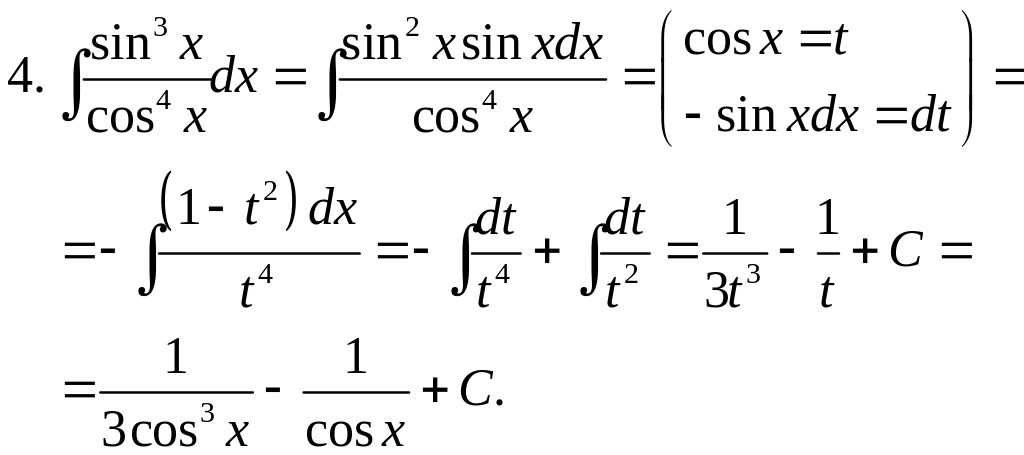
3) Если
подынтегральная функция четна и
относительно
,
и относительно
,
т.е.
,
то замена
рационализирует интеграл (14).
Воспользуемся тригонометрическими равенствами:
.
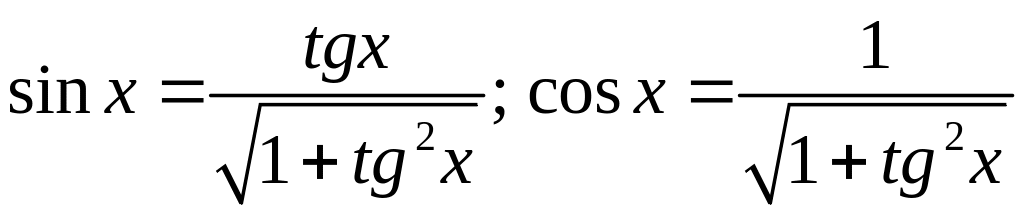Найдем дифференциал .
.
Окончательно получим замену:
.
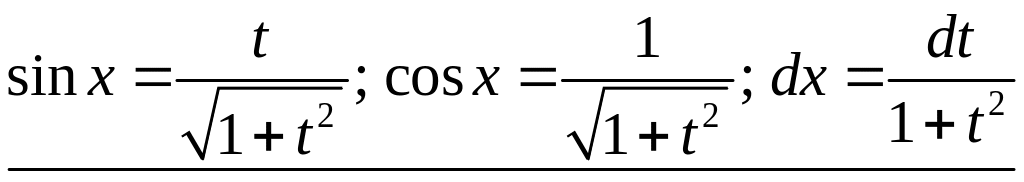Примеры.
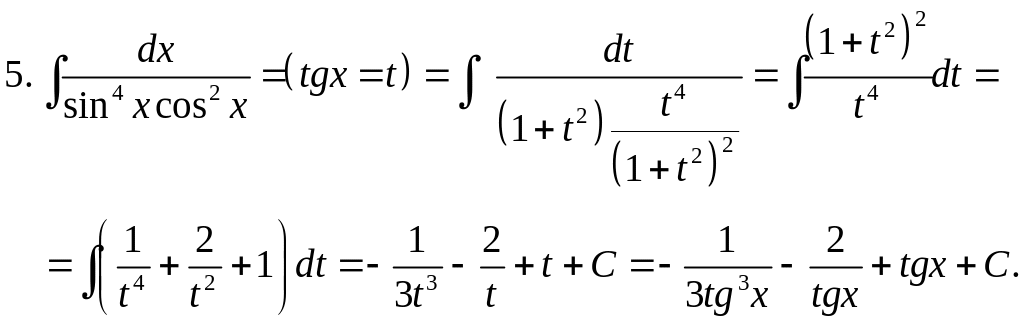
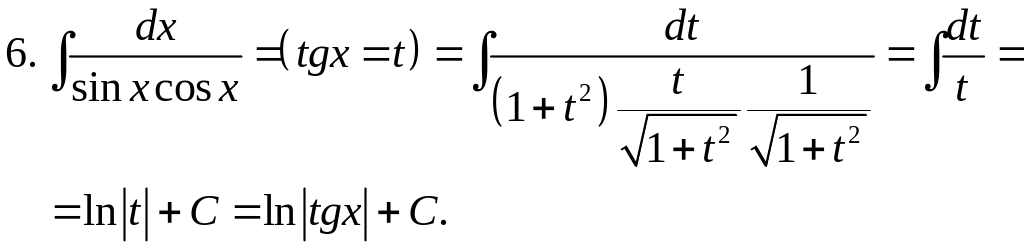
2.9. Интегрирование некоторых иррациональных функций
Интегрирование не всякого иррационального выражения возможно в элементарных функциях. В некоторых простейших случаях иррациональные функции можно рационализировать с помощью замены переменной, а значит, и проинтегрировать в конечном виде.
1.
Интегрирование функций вида
.
Здесь
символ
указывает, что над величинами
выполняются только рациональные
операции: сложение, вычитание, умножение,
и деление. Например:
.
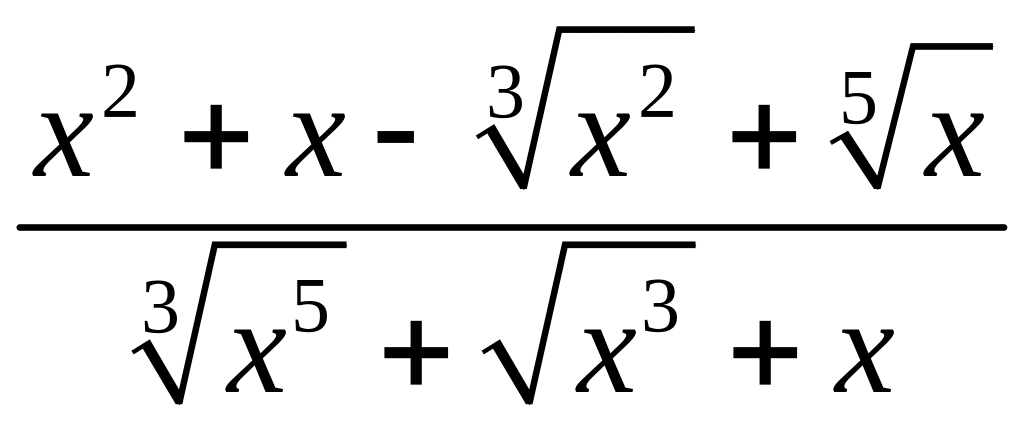Пусть
надо вычислить интеграл
,
где числа m, n,…
могут быть и отрицательными. Подберём
число N так, чтобы при
замене переменной
все корни извлекались. (N
– НОК чисел m, n,…).
Тогда:
и
=
.
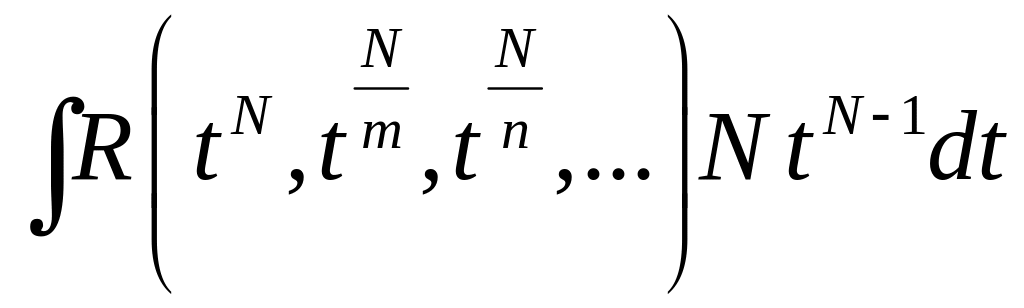Так
как все числа
;
– целые, то подынтегральная функция не
содержит дробных степеней t,
т.е. является дробно-рациональной
функцией от t.
Примеры.
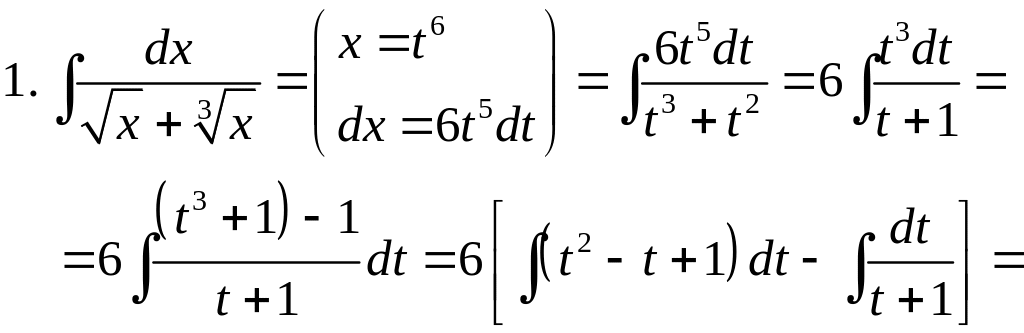
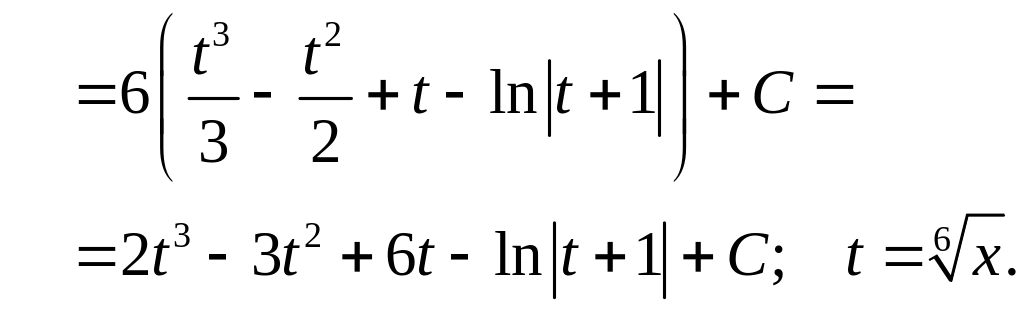
2.
.
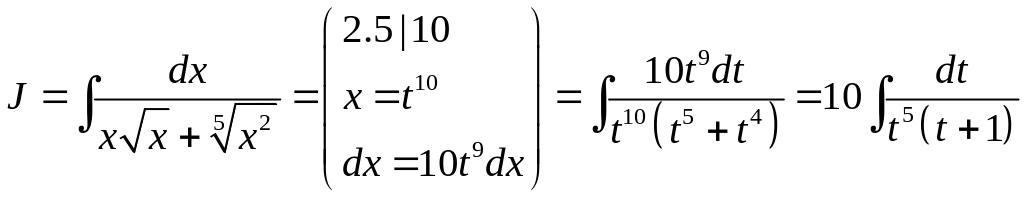Выбранная замена свела интеграл от иррационального выражения к интегралу от рациональной дроби. Разложим дробь на простейшие.
.
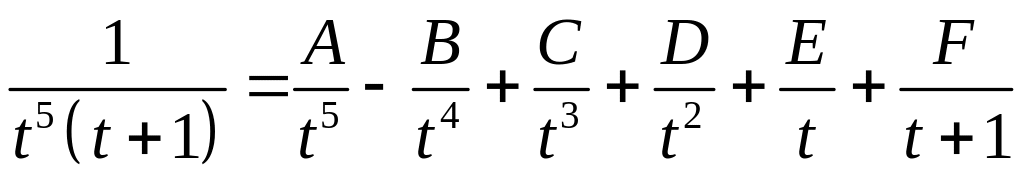Найдем неизвестные коэффициенты:
.
.
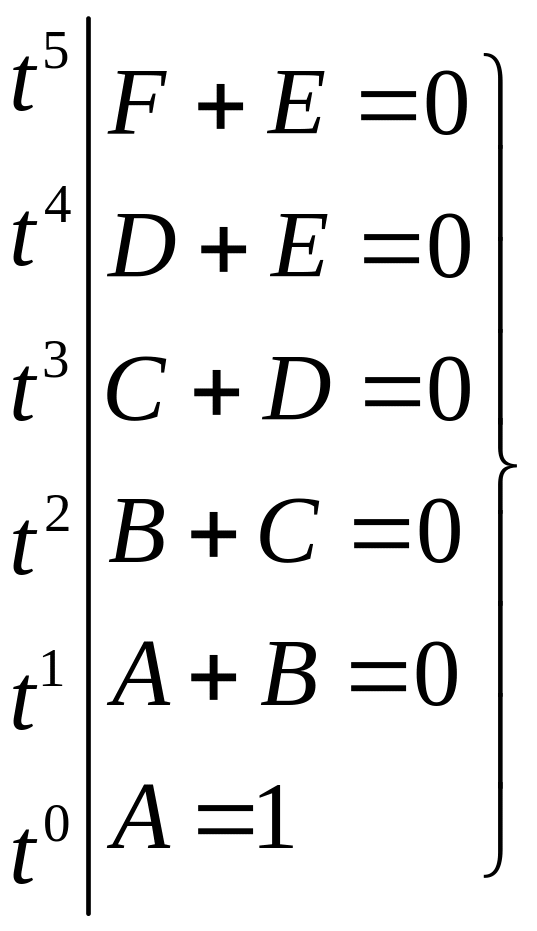
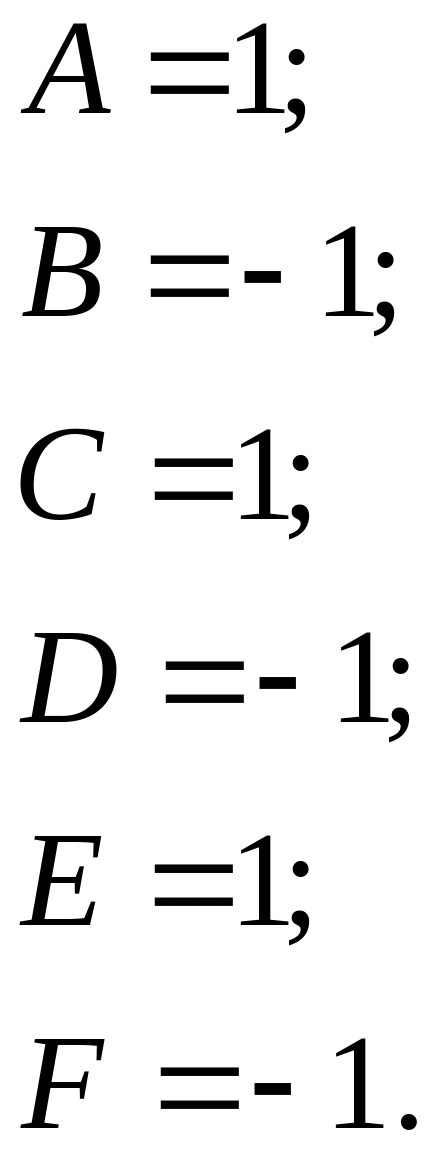
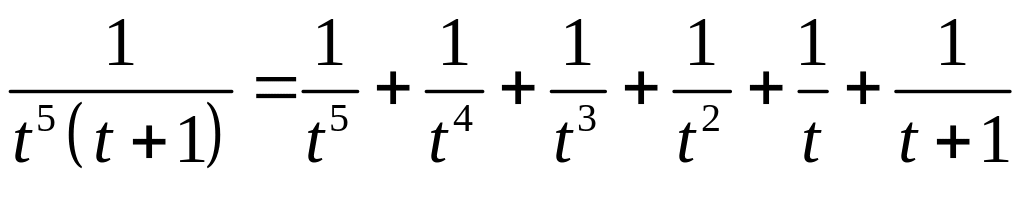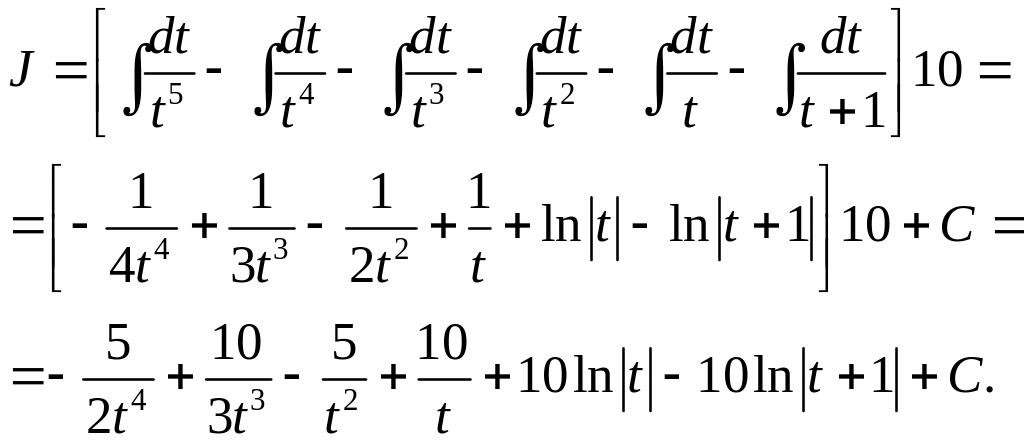
Вернемся к старой переменной
.
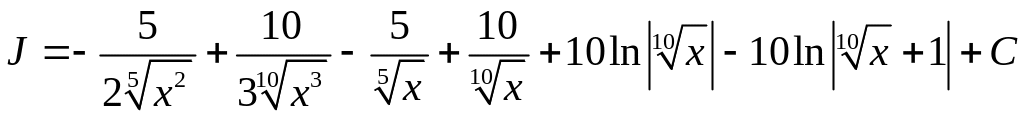2.
Интегрирование выражений вида
.
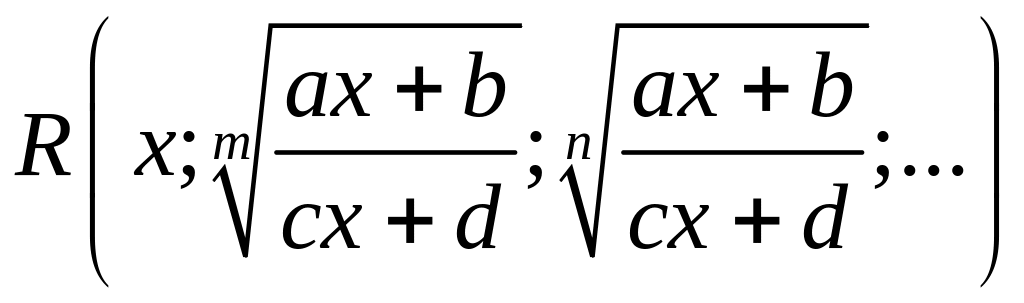Ничего не изменяется по сравнению с предыдущим случаем, если все подкоренные выражения являются одной и той же дробно-рациональной функцией. В этом случае делаем замену:
,
где N – наименьшее общее кратное чисел m, n,….
Находим
:
.
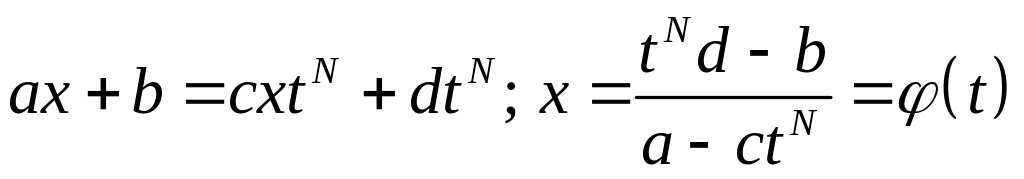Здесь – рациональная функция от , поэтому – тоже рациональная функция. Значит, и является рациональным выражением. Таким образом, получаем:
.
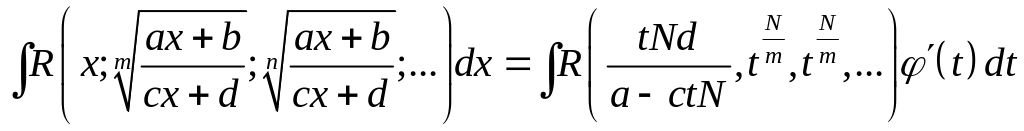Здесь
- целые числа. Поэтому получили интеграл
от дробно-рациональной функции от
.
Примеры.
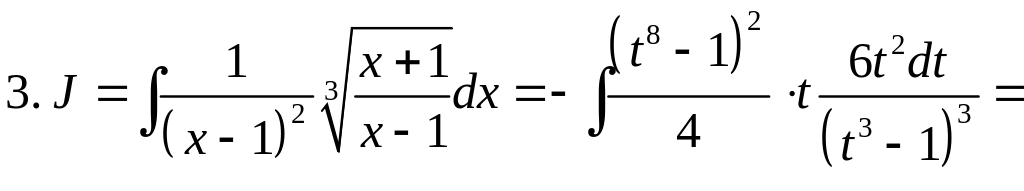
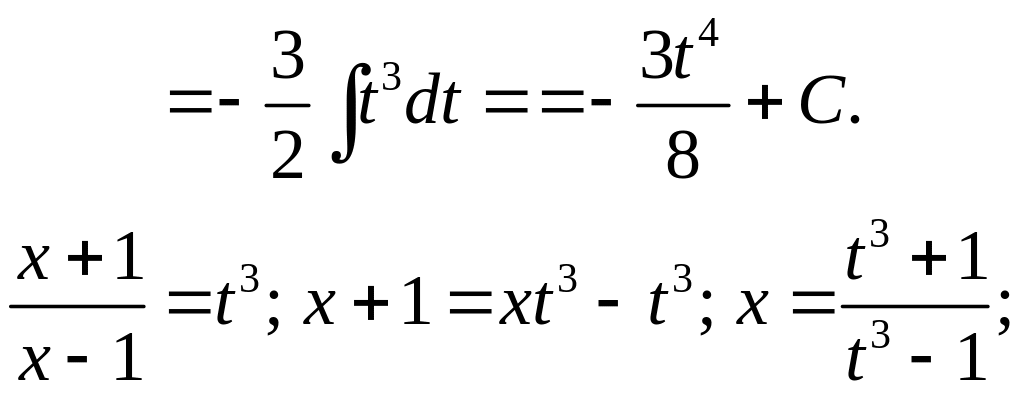
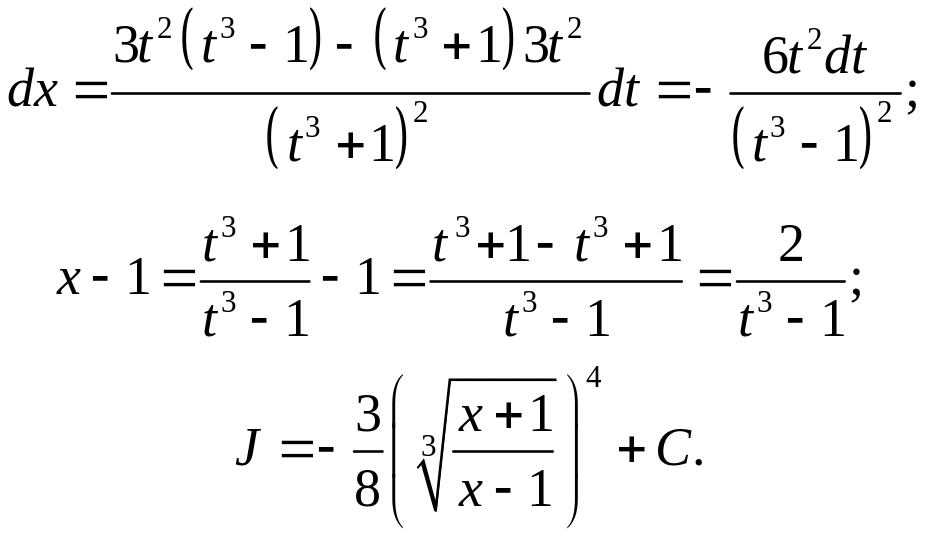
4.
.
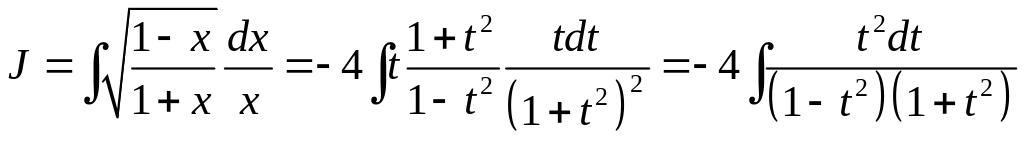Была сделана замена
.
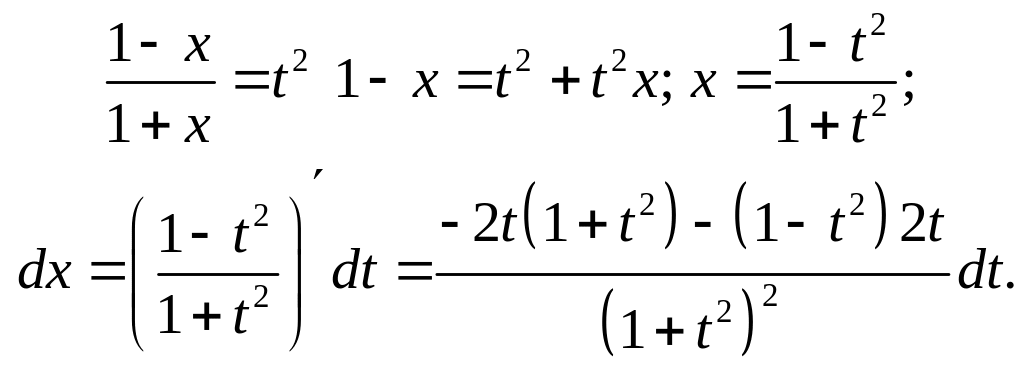
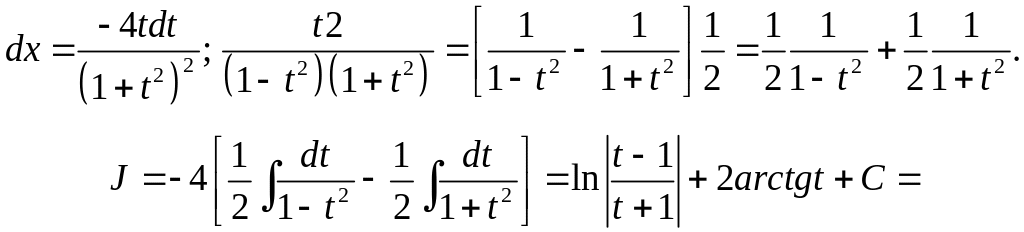
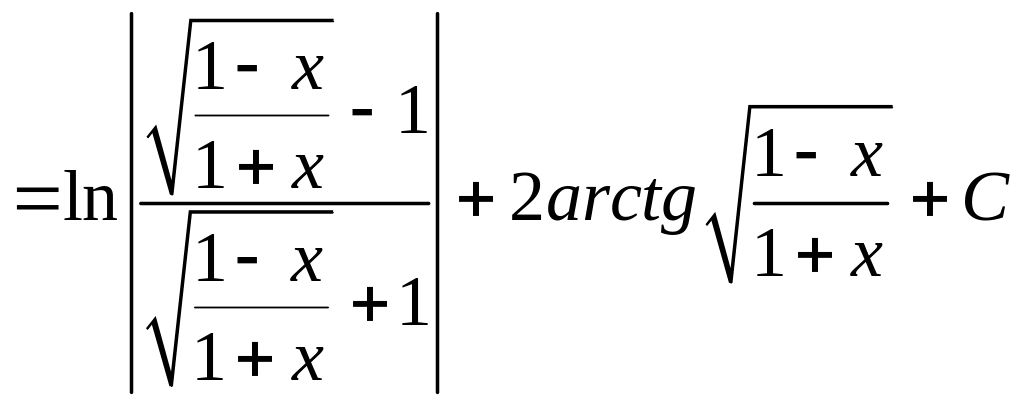3.
Интегрирование выражений вида
.
Интеграл
преобразуем к новой переменной,
предварительно выделив полный квадрат:
.
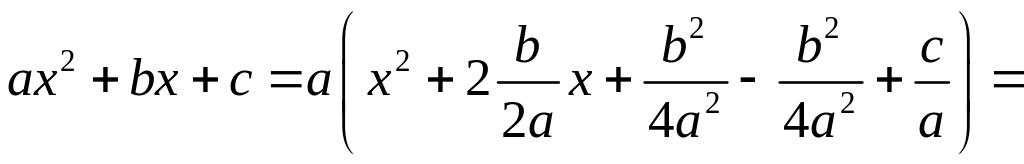
Полагаем:
.
Тогда, если
1.
,
то
,
где
;
2.
,
то
,
где
;
3.
,
то
,
где
.
Полученные интегралы рационализируются, например, с помощью тригонометрических подстановок:
1.
.
.
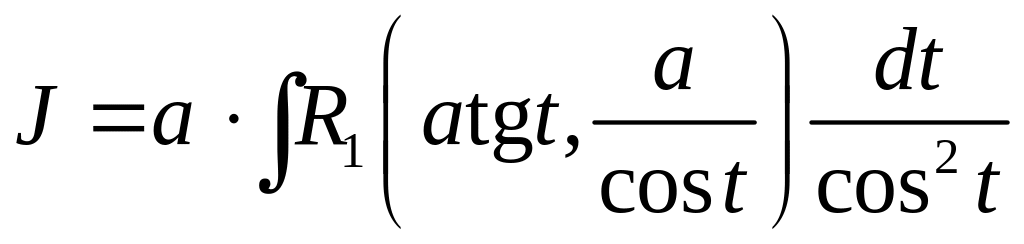2.
.
.
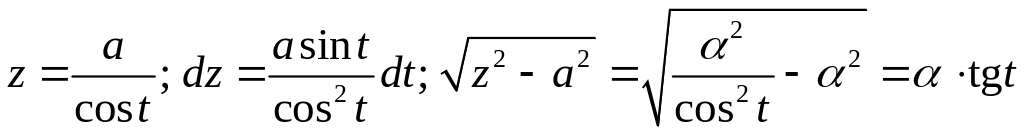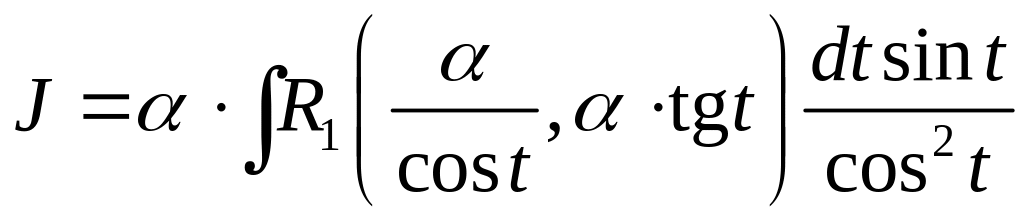3.
,
.
Примеры.
5.
