§ 2.16. Полярна система координат. Параметричні рівняння лінії.

Найбільш важливою після прямокутної системи координат на площині вважається полярна система координат . Ця система також дозволяє визначати положення будь-якої точки на площині за допомогою двох чисел – її координат. Полярна система координат складається з деякої точки О, яка називається полюсом і напрямленої напівпрямої ОЕ, яка виходить із точки О і називається полярною віссю (рис. 18).

Крім того, необхідно задати відрізок одиничної довжини.

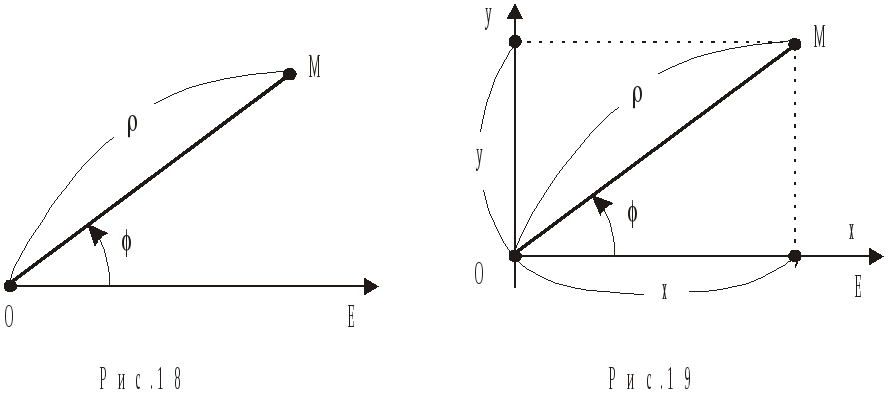
Нехай на площині задані полярна система координат і точка М. З’єднаємо полюс О з точкою М. Довжина здобутого відрізку ρ=|OM| називається полярним радіусом точки М, а кут ( кут відлічується від осі ОЕ до відрізку ОМ проти руху годинникової стрілки) – полярним кутом (рис. 18). Числа  і  є відповідно першою й другою полярними координатами точки М (пишеться М(,)). Можливі значення полярних координат, як правило, визначаються нерівностями , . Інколи вказані області значень розширюються. Наприклад, якщо кут  відлічувати від осі ОЕ за рухом годинникової стрілки, то його значення береться від’ємним. Існує узагальнення полярної системи, в якому ρ також може приймати від’ємні значення.

Якщо на площині задані прямокутна й полярна системи координат, причому полярна вісь ОЕ співпадає з додатною напіввіссю ОХ (рис. 19), то між полярними й прямокутними координатами існує зв’язок:

(16.1)

(16.2)

Формули (16.1) виражають декартові координати через полярні, а формули (16.2) – полярні через декартові. Друга з формул (16.2) дає два значення координати  із проміжку [0;2). Необхідно взяти те з них, яке задовольняє рівнянням (16.1).

Приклад 1. Відмітити на площині точки ), що задані полярними координатами.

Розв’язання. Для побудови точки М з полярного полюса проводимо промінь під кутом до полярної осі і відкладаємо на ньому відрізок довжиною 3. Точки М і М будуються подібно (рис. 20).

Приклад 2. Побудувати лінію .

Розв’язання. Врахуємо, що так як , то  може приймати значення лише на відрізку [0;] (на цьому відрізку ). Знаходимо координати деяких точок даної лінії і записуємо їх у таблицю.

	0
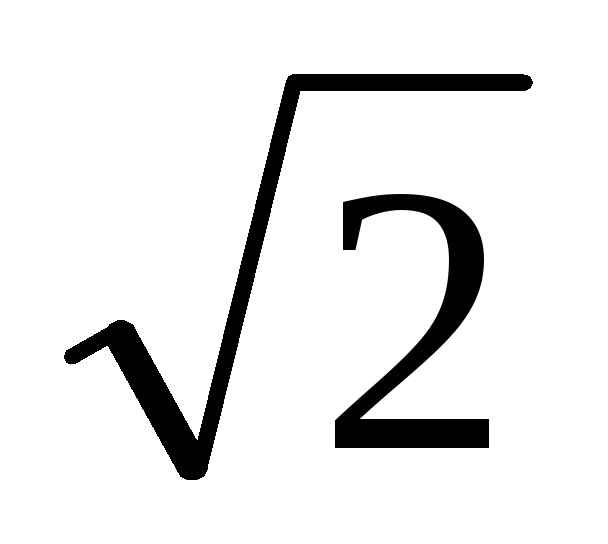
	0		2		0

Відмічаємо знайдені точки на площині і з’єднуємо їх плавною лінією (рис. 21).

Приклад 3 В прямокутній системі координат коло задане рівнянням Знайти рівняння цього кола в полярних координатах, вважаючи, що полярна вісь співпадає з додатною напіввісью Ох.

Розв’язання. Використовуючи формули (16.1), маємо

Як бачимо, в полярній системі координат рівняння кола значно простіше, ніж у декартовій.

При розв’язанні багатьох прикладних задач зручно використовувати так звані параметричні рівняння лінії, тобто, рівняння, в яких координати точок лінії задаються у вигляді функцій від деякої змінної величини t (параметра). Для таких рівнянь прийнятий запис . Якщо в параметричних рівняннях виключити параметр t, то здобудемо звичайне рівняння лінії.

Приклад4. Крива задана параметричними рівняннями Побудувати дану криву і визначити її тип.

Розв’язання. Визначаємо координати деяких точок лінії і заносимо їх у таблицю (очевидно, що параметр t достатньо змінювати від 0 до 2).

t	0
x
y

Використовуючи знайдені точки, будуємо криву (рис. 22).

Дана лінія дуже схожа на еліпс. Переконаємося, що це справді так (виключаємо параметр t):

, .